Основные типы сигналов

Вот несколько основных сигналов:

Единица Шаг Функция

Функция единичного шага обозначается u (t). Он определяется как u (t) = $ \ left \ {\ begin {matrix} 1 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $

• Он используется как лучший тестовый сигнал.
• Площадь под функцией шага единицы измерения равна единице.

Единица импульсная функция

Импульсная функция обозначается δ (t). и определяется как δ (t) = $ \ left \ {\ begin {matrix} 1 & t = 0 \\ 0 & t \ neq 0 \ end {matrix} \ right. $

$$ \ int _ {- \ infty} ^ {\ infty} δ (t) dt = u (t) $$

$$ \ delta (t) = {du (t) \ over dt} $$

Сигнал рампы

Сигнал рампы обозначается r (t), и он определяется как r (t) = $ \ left \ {\ begin {matrix} t & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right . $

$$ \ int u (t) = \ int 1 = t = r (t) $$

$$ u (t) = {dr (t) \ over dt} $$

Площадь под рампой агрегата равна единице.

Параболический сигнал

Параболический сигнал можно определить как x (t) = $ \ left \ {\ begin {matrix} t ^ 2/2 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $

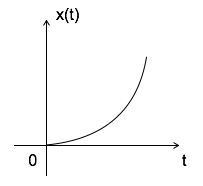
$$ \ iint u (t) dt = \ int r (t) dt = \ int t dt = {t ^ 2 \ over 2} = параболический сигнал $$

$$ \ Rightarrow u (t) = {d ^ 2x (t) \ over dt ^ 2} $$

$$ \ Rightarrow r (t) = {dx (t) \ over dt} $$

Сигнум Функция

Сигнум-функция обозначается как sgn (t). Он определяется как sgn (t) = $ \ left \ {\ begin {matrix} 1 & t> 0 \\ 0 & t = 0 \\ -1 & t <0 \ end {matrix} \ right. $

Экспоненциальный сигнал

Экспоненциальный сигнал имеет вид x (t) = $ e ^ {\ alpha t} $.

Форму экспоненты можно определить с помощью $ \ alpha $.

Case i: если $ \ alpha $ = 0 $ \ to $ x (t) = $ e ^ 0 $ = 1

Case ii:если $ \ alpha $ <0 ie -ve, то x (t) = $ e ^ {- \ alpha t} $. Форма называется убывающей экспоненциальной.

Case iii:если $ \ alpha $> 0 ie + ve, то x (t) = $ e ^ {\ alpha t} $. Форма называется восходящей экспоненциальной.

Прямоугольный сигнал

Обозначим его как x (t) и определим как

Треугольный сигнал

Обозначим его как x (t)

Синусоидальный сигнал

Синусоидальный сигнал имеет вид x (t) = A cos ($ {w} _ {0} \, \ pm \ phi $) или A sin ($ {w} _ {0} \, \ pm \ phi $ )

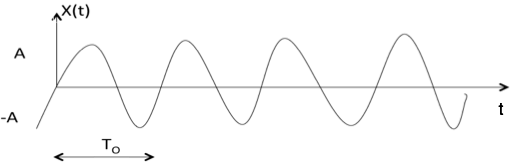
Где T ₀ = $ 2 \ pi \ over {w} _ {0} $

Функция Sinc

Он обозначается как sinc (t) и определяется как sinc

$$ (t) = {sin \ pi t \ over \ pi t} $$

$$ = 0 \, \ text {для t} = \ pm 1, \ pm 2, \ pm 3 ... $$

Функция выборки

Он обозначается как sa (t) и определяется как

$$ sa (t) = {sin t \ over t} $$

$$ = 0 \, \, \ text {для t} = \ pm \ pi, \, \ pm 2 \ pi, \, \ pm 3 \ pi \, ... $$