การสื่อสารแบบอนาล็อก - การมอดูเลต VSBSC
ในบทก่อนหน้านี้เราได้กล่าวถึงการมอดูเลต SSBSC และการดีมอดูเลต สัญญาณมอดูเลต SSBSC มีความถี่ไซด์แบนด์เดียว ในทางทฤษฎีเราสามารถหาส่วนประกอบความถี่ไซด์แบนด์ได้อย่างสมบูรณ์โดยใช้ตัวกรองแบนด์พาสในอุดมคติ อย่างไรก็ตามในทางปฏิบัติเราอาจไม่ได้รับส่วนประกอบความถี่ไซด์แบนด์ทั้งหมด ด้วยเหตุนี้ข้อมูลบางส่วนจึงสูญหายไป
เพื่อหลีกเลี่ยงการสูญเสียนี้จึงเลือกใช้เทคนิคซึ่งเป็นการประนีประนอมระหว่าง DSBSC และ SSBSC เทคนิคนี้เรียกว่าVestigial Side Band Suppressed Carrier (VSBSC)เทคนิค. คำว่า "ร่องรอย" หมายถึง "ส่วนหนึ่ง" ซึ่งมาจากชื่อนี้
VSBSC Modulationเป็นกระบวนการที่ส่วนหนึ่งของสัญญาณที่เรียกว่า vestige ถูกมอดูเลตพร้อมกับแถบด้านข้างหนึ่ง สเปกตรัมความถี่ของคลื่น VSBSC แสดงดังรูปต่อไปนี้

นอกเหนือจากแถบด้านข้างด้านบนแล้วส่วนหนึ่งของแถบด้านข้างด้านล่างจะถูกส่งไปในเทคนิคนี้ด้วย ในทำนองเดียวกันเราสามารถส่งแถบด้านข้างด้านล่างพร้อมกับส่วนหนึ่งของแถบด้านข้างด้านบน แถบป้องกันที่มีความกว้างน้อยมากวางไว้ที่ด้านใดด้านหนึ่งของ VSB เพื่อหลีกเลี่ยงการรบกวน การมอดูเลต VSB ส่วนใหญ่จะใช้ในการส่งสัญญาณโทรทัศน์
แบนด์วิดท์ของการมอดูเลต VSBSC
เราทราบว่าแบนด์วิดท์ของคลื่นมอดูเลต SSBSC คือ $ f_m $ เนื่องจากคลื่นมอดูเลต VSBSC มีส่วนประกอบความถี่ของแถบด้านหนึ่งพร้อมกับร่องรอยของแถบด้านข้างอื่น ๆ แบนด์วิดท์ของมันจะเป็นผลรวมของแบนด์วิดท์ของคลื่นมอดูเลต SSBSC และความถี่ร่องรอย $ f_v $
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
ข้อดี
ต่อไปนี้เป็นข้อดีของการมอดูเลต VSBSC
มีประสิทธิภาพสูง
ลดแบนด์วิดท์เมื่อเทียบกับคลื่น AM และ DSBSC
การออกแบบตัวกรองทำได้ง่ายเนื่องจากไม่ต้องการความแม่นยำสูง
การส่งส่วนประกอบความถี่ต่ำทำได้โดยไม่มีปัญหาใด ๆ
มีลักษณะเฟสที่ดี
ข้อเสีย
ต่อไปนี้เป็นข้อเสียของการมอดูเลต VSBSC
แบนด์วิดท์มากกว่าเมื่อเทียบกับคลื่น SSBSC
Demodulation มีความซับซ้อน
การใช้งาน
การประยุกต์ใช้ VSBSC ที่โดดเด่นที่สุดและเป็นมาตรฐานสำหรับการส่งสัญญาณโทรทัศน์ นอกจากนี้นี่เป็นเทคนิคที่สะดวกและมีประสิทธิภาพที่สุดเมื่อพิจารณาการใช้แบนด์วิดท์
ตอนนี้ให้เราพูดคุยเกี่ยวกับโมดูเลเตอร์ที่สร้างคลื่น VSBSC และตัวดีโมดูเลเตอร์ซึ่งสาธิตคลื่น VSBSC ทีละตัว
การสร้าง VSBSC
การสร้างคลื่น VSBSC คล้ายกับการสร้างคลื่น SSBSC โมดูเลเตอร์ VSBSC แสดงในรูปต่อไปนี้
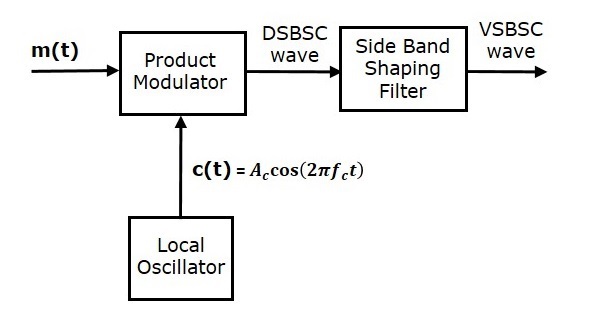
ในวิธีนี้อันดับแรกเราจะสร้างคลื่น DSBSC ด้วยความช่วยเหลือของโมดูเลเตอร์ผลิตภัณฑ์ จากนั้นใช้คลื่น DSBSC นี้เป็นอินพุตของตัวกรองการสร้างแถบด้านข้าง ตัวกรองนี้สร้างเอาต์พุตซึ่งเป็นคลื่น VSBSC
สัญญาณมอดูเลต $ m \ left (t \ right) $ และสัญญาณผู้ให้บริการ $ A_c \ cos \ left (2 \ pi f_ct \ right) $ ถูกนำไปใช้เป็นอินพุตไปยังโมดูเลเตอร์ของผลิตภัณฑ์ ดังนั้นโมดูเลเตอร์ผลิตภัณฑ์จึงสร้างเอาต์พุตซึ่งเป็นผลคูณของอินพุตทั้งสองนี้
ดังนั้นผลลัพธ์ของโมดูเลเตอร์ผลิตภัณฑ์คือ
$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
ใช้การแปลงฟูเรียร์ทั้งสองด้าน
$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$
สมการข้างต้นแสดงถึงสมการของสเปกตรัมความถี่ DSBSC
ให้ฟังก์ชันการถ่ายโอนของตัวกรองการสร้างแถบด้านข้างเป็น $ H \ left (f \ right) $ ตัวกรองนี้มีอินพุต $ p \ left (t \ right) $ และเอาต์พุตคือ VSBSC modulated wave $ s \ left (t \ right) $ การแปลงฟูเรียร์ของ $ p \ left (t \ right) $ และ $ s \ left (t \ right) $ คือ $ P \ left (t \ right) $ และ $ S \ left (t \ right) $ ตามลำดับ
ในทางคณิตศาสตร์เราสามารถเขียน $ S \ left (f \ right) $ เป็น
$$ S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right) $$
แทนค่า $ P \ left (f \ right) $ ในสมการด้านบน
$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right) $$
สมการข้างต้นแสดงถึงสมการของสเปกตรัมความถี่ VSBSC
Demodulation ของ VSBSC
Demodulation ของ VSBSC wave คล้ายกับ demodulation ของ SSBSC wave ที่นี่สัญญาณพาหะเดียวกัน (ซึ่งใช้สำหรับสร้างคลื่น VSBSC) ถูกใช้เพื่อตรวจจับสัญญาณข้อความ ดังนั้นกระบวนการตรวจจับนี้จึงเรียกว่าcoherent หรือ synchronous detection. VSBSC demodulator แสดงดังรูปต่อไปนี้

ในกระบวนการนี้สัญญาณข้อความสามารถดึงออกมาจากคลื่น VSBSC ได้โดยการคูณกับพาหะซึ่งมีความถี่เดียวกันและเฟสของพาหะที่ใช้ในการมอดูเลต VSBSC จากนั้นสัญญาณที่ได้จะถูกส่งผ่าน Low Pass Filter เอาต์พุตของตัวกรองนี้คือสัญญาณข้อความที่ต้องการ
ให้คลื่น VSBSC เป็น $ s \ left (t \ right) $ และสัญญาณพาหะคือ $ A_c \ cos \ left (2 \ pi f_ct \ right) $
จากรูปเราสามารถเขียนผลลัพธ์ของโมดูเลเตอร์ผลิตภัณฑ์เป็น
$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$
ใช้การแปลงฟูเรียร์ทั้งสองด้าน
$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$
เรารู้ว่า$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ ซ้าย (f \ right) $
จากสมการด้านบนให้เราหา $ S \ left (f-f_c \ right) $ และ $ S \ left (f + f_c \ right) $
$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ ขวา] H \ left (f-f_c \ right) $$
$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right) $
$$ S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ ขวา] H \ left (f + f_c \ right) $$
$ \ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right) $
แทนที่ $ S \ left (f-f_c \ right) $ และ $ S \ left (f + f_c \ right) $ ค่าใน $ V \ left (f \ right) $
$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $
$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $
$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ right) H \ left (f + f_c \ right) \ right] $
ในสมการข้างต้นคำแรกแสดงถึงเวอร์ชันที่ปรับขนาดของสเปกตรัมความถี่สัญญาณข้อความที่ต้องการ สามารถสกัดได้โดยส่งสัญญาณข้างต้นผ่านตัวกรองความถี่ต่ำ
$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $$