ทฤษฎีเรโซแนนซ์แบบปรับได้

เครือข่ายนี้ได้รับการพัฒนาโดย Stephen Grossberg และ Gail Carpenter ในปี 1987 โดยอาศัยการแข่งขันและใช้รูปแบบการเรียนรู้ที่ไม่มีผู้ดูแล เครือข่าย Adaptive Resonance Theory (ART) ตามชื่อที่แนะนำนั้นเปิดกว้างสำหรับการเรียนรู้ใหม่ ๆ (ปรับตัว) ได้เสมอโดยไม่สูญเสียรูปแบบเก่า ๆ (การสั่นพ้อง) โดยทั่วไปเครือข่าย ART เป็นลักษณนามเวกเตอร์ซึ่งรับเวกเตอร์อินพุตและจำแนกเป็นประเภทใดประเภทหนึ่งขึ้นอยู่กับรูปแบบที่จัดเก็บไว้ซึ่งคล้ายคลึงกันมากที่สุด

หัวหน้าฝ่ายปฏิบัติการ

การดำเนินการหลักของการจำแนกประเภท ART สามารถแบ่งออกเป็นขั้นตอนต่อไปนี้ -

Recognition phase- เวกเตอร์อินพุตถูกเปรียบเทียบกับการจำแนกประเภทที่นำเสนอในทุกโหนดในเลเยอร์เอาต์พุต ผลลัพธ์ของเซลล์ประสาทจะกลายเป็น“ 1” ถ้าตรงกับการจำแนกที่ใช้มากที่สุดมิฉะนั้นจะกลายเป็น“ 0”
Comparison phase- ในขั้นตอนนี้จะทำการเปรียบเทียบเวกเตอร์อินพุตกับเวกเตอร์เลเยอร์เปรียบเทียบ เงื่อนไขสำหรับการรีเซ็ตคือระดับของความคล้ายคลึงกันจะน้อยกว่าพารามิเตอร์การเฝ้าระวัง
Search phase- ในขั้นตอนนี้เครือข่ายจะค้นหาการรีเซ็ตและการจับคู่ที่ทำในขั้นตอนข้างต้น ดังนั้นหากไม่มีการรีเซ็ตและการแข่งขันค่อนข้างดีการจัดประเภทจะสิ้นสุดลง มิฉะนั้นกระบวนการจะซ้ำและต้องส่งรูปแบบอื่น ๆ ที่จัดเก็บไว้เพื่อค้นหาการจับคู่ที่ถูกต้อง

ART1

เป็น ART ประเภทหนึ่งซึ่งออกแบบมาเพื่อจัดกลุ่มเวกเตอร์ไบนารี เราสามารถเข้าใจเกี่ยวกับเรื่องนี้ด้วยสถาปัตยกรรมของมัน

สถาปัตยกรรมของ ART1

ประกอบด้วยสองหน่วยต่อไปนี้ -

Computational Unit - ประกอบด้วยสิ่งต่อไปนี้ -

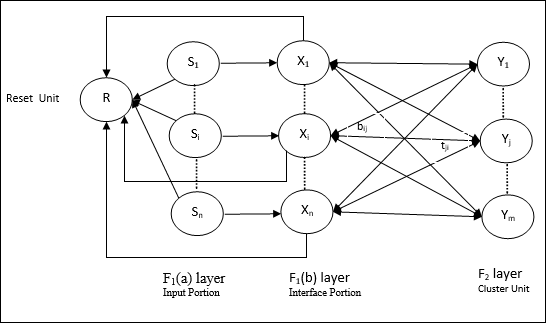
Input unit (F₁ layer) - นอกจากนี้ยังมีสองส่วนต่อไปนี้ -
- F₁(a) layer (Input portion)- ใน ART1 จะไม่มีการประมวลผลในส่วนนี้แทนที่จะมีเวกเตอร์อินพุตเท่านั้น เชื่อมต่อกับเลเยอร์F ₁ (b) (ส่วนอินเตอร์เฟส)
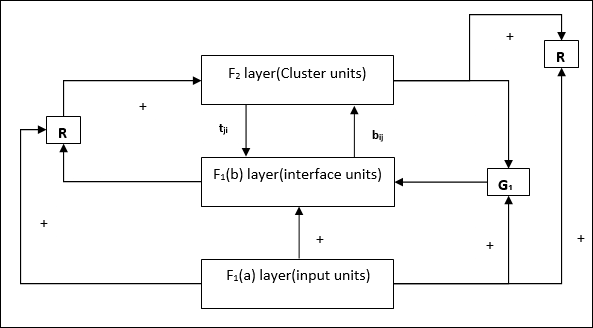
- F₁(b) layer (Interface portion)- ส่วนนี้รวมสัญญาณจากส่วนอินพุตกับเลเยอร์F ₂เลเยอร์F ₁ (b) เชื่อมต่อกับเลเยอร์F ₂โดยใช้น้ำหนักจากล่างขึ้นบนb_ijและชั้นF ₂เชื่อมต่อกับชั้น F ₁ (b) ผ่านน้ำหนักจากบนลงล่างt_ji.
Cluster Unit (F₂ layer)- นี่คือเลเยอร์การแข่งขัน หน่วยที่มีอินพุตสุทธิที่ใหญ่ที่สุดถูกเลือกเพื่อเรียนรู้รูปแบบการป้อนข้อมูล การเปิดใช้งานหน่วยคลัสเตอร์อื่น ๆ ทั้งหมดถูกตั้งค่าเป็น 0
Reset Mechanism- การทำงานของกลไกนี้ขึ้นอยู่กับความคล้ายคลึงกันระหว่างน้ำหนักจากบนลงล่างและเวกเตอร์อินพุต ตอนนี้ถ้าระดับของความคล้ายคลึงกันนี้น้อยกว่าพารามิเตอร์การเฝ้าระวังคลัสเตอร์จะไม่ได้รับอนุญาตให้เรียนรู้รูปแบบและส่วนที่เหลือจะเกิดขึ้น

Supplement Unit - จริงๆแล้วปัญหาเกี่ยวกับกลไกการรีเซ็ตก็คือเลเยอร์ F₂จะต้องถูกยับยั้งภายใต้เงื่อนไขบางประการและจะต้องพร้อมใช้งานเมื่อเกิดการเรียนรู้บางอย่าง นั่นคือเหตุผลที่หน่วยเสริมสองหน่วย ได้แก่G₁ และ G₂ ถูกเพิ่มพร้อมกับหน่วยรีเซ็ต R. พวกเขาเรียกว่าgain control units. หน่วยเหล่านี้รับและส่งสัญญาณไปยังหน่วยอื่น ๆ ที่มีอยู่ในเครือข่าย‘+’ บ่งบอกถึงสัญญาณกระตุ้นในขณะที่ ‘−’ บ่งบอกถึงสัญญาณยับยั้ง