โครงข่ายประสาทเทียม - คู่มือฉบับย่อ

เครือข่ายประสาทเทียมเป็นอุปกรณ์คอมพิวเตอร์แบบขนานซึ่งโดยพื้นฐานแล้วเป็นความพยายามที่จะสร้างแบบจำลองคอมพิวเตอร์ของสมอง วัตถุประสงค์หลักคือการพัฒนาระบบให้ทำงานด้านการคำนวณต่างๆได้เร็วกว่าระบบแบบเดิม งานเหล่านี้รวมถึงการจดจำและการจำแนกรูปแบบการประมาณการเพิ่มประสิทธิภาพและการจัดกลุ่มข้อมูล

โครงข่ายประสาทเทียมคืออะไร?

โครงข่ายประสาทเทียม (ANN) เป็นระบบคอมพิวเตอร์ที่มีประสิทธิภาพซึ่งมีธีมหลักที่ยืมมาจากการเปรียบเทียบเครือข่ายประสาททางชีววิทยา ANN ยังได้รับการตั้งชื่อเป็น "ระบบประสาทเทียม" หรือ "ระบบประมวลผลแบบกระจายคู่ขนาน" หรือ "ระบบเชื่อมต่อ" ANN ได้รับคอลเลกชันจำนวนมากของหน่วยที่เชื่อมต่อกันในบางรูปแบบเพื่อให้สามารถสื่อสารระหว่างหน่วยได้ หน่วยเหล่านี้เรียกอีกอย่างว่าโหนดหรือเซลล์ประสาทเป็นตัวประมวลผลอย่างง่ายซึ่งทำงานแบบขนาน

เซลล์ประสาททุกเซลล์เชื่อมต่อกับเซลล์ประสาทอื่น ๆ ผ่านลิงค์การเชื่อมต่อ แต่ละลิงค์เชื่อมต่อมีน้ำหนักที่มีข้อมูลเกี่ยวกับสัญญาณอินพุต นี่เป็นข้อมูลที่มีประโยชน์ที่สุดสำหรับเซลล์ประสาทในการแก้ปัญหาโดยเฉพาะเนื่องจากน้ำหนักมักจะกระตุ้นหรือยับยั้งสัญญาณที่กำลังสื่อสาร เซลล์ประสาทแต่ละเซลล์มีสถานะภายในซึ่งเรียกว่าสัญญาณกระตุ้น สัญญาณเอาท์พุตซึ่งสร้างขึ้นหลังจากรวมสัญญาณอินพุตและกฎการเปิดใช้งานอาจถูกส่งไปยังหน่วยอื่น

ประวัติย่อของ ANN

ประวัติของ ANN สามารถแบ่งออกเป็นสามยุคดังต่อไปนี้ -

ANN ในช่วงทศวรรษที่ 1940 ถึง 1960

พัฒนาการที่สำคัญบางประการในยุคนี้มีดังนี้ -

• 1943 - มีการสันนิษฐานว่าแนวคิดของโครงข่ายประสาทเทียมเริ่มต้นจากการทำงานของนักสรีรวิทยาวอร์เรนแมคคัลล็อกและนักคณิตศาสตร์วอลเตอร์พิตส์เมื่อในปีพ. ศ. 2486 พวกเขาได้สร้างแบบจำลองเครือข่ายประสาทที่เรียบง่ายโดยใช้วงจรไฟฟ้าเพื่ออธิบายว่าเซลล์ประสาทในสมองอาจทำงานได้อย่างไร .

• 1949- หนังสือของโดนัลด์เฮบบ์เรื่องThe Organization of Behaviorกล่าวถึงความจริงที่ว่าการกระตุ้นเซลล์ประสาทหนึ่งซ้ำ ๆ โดยอีกเซลล์หนึ่งจะเพิ่มความแข็งแรงทุกครั้งที่ใช้

• 1956 - เครือข่ายหน่วยความจำเชื่อมโยงได้รับการแนะนำโดย Taylor

• 1958 - วิธีการเรียนรู้สำหรับแบบจำลองเซลล์ประสาท McCulloch และ Pitts ชื่อ Perceptron ถูกคิดค้นโดย Rosenblatt

• 1960 - Bernard Widrow และ Marcian Hoff พัฒนาโมเดลที่เรียกว่า "ADALINE" และ "MADALINE"

ANN ในช่วงปี 1960 ถึง 1980

พัฒนาการที่สำคัญบางประการในยุคนี้มีดังนี้ -

• 1961 - Rosenblatt ทำไม่สำเร็จ แต่เสนอโครงการ "backpropagation" สำหรับเครือข่ายหลายชั้น

• 1964 - เทย์เลอร์สร้างวงจรผู้ชนะ - รับทั้งหมดโดยมีการยับยั้งระหว่างหน่วยเอาต์พุต

• 1969 - Multilayer perceptron (MLP) ถูกคิดค้นโดย Minsky และ Papert

• 1971 - Kohonen พัฒนาความทรงจำ Associative

• 1976 - Stephen Grossberg และ Gail Carpenter ได้พัฒนาทฤษฎี Adaptive resonance

ANN ตั้งแต่ปี 1980 จนถึงปัจจุบัน

พัฒนาการที่สำคัญบางประการในยุคนี้มีดังนี้ -

• 1982 - การพัฒนาที่สำคัญคือแนวทางด้านพลังงานของ Hopfield

• 1985 - เครื่อง Boltzmann ได้รับการพัฒนาโดย Ackley, Hinton และ Sejnowski

• 1986 - Rumelhart, Hinton และ Williams แนะนำ Generalized Delta Rule

• 1988 - Kosko พัฒนา Binary Associative Memory (BAM) และยังให้แนวคิดเรื่อง Fuzzy Logic ใน ANN

การทบทวนในอดีตแสดงให้เห็นว่ามีความคืบหน้าอย่างมีนัยสำคัญในสาขานี้ ชิปบนเครือข่ายประสาทเทียมกำลังเกิดขึ้นและมีการพัฒนาแอปพลิเคชันสำหรับปัญหาที่ซับซ้อน แน่นอนว่าวันนี้เป็นช่วงแห่งการเปลี่ยนแปลงของเทคโนโลยีเครือข่ายประสาทเทียม

เซลล์ประสาททางชีวภาพ

เซลล์ประสาท (neuron) เป็นเซลล์ทางชีววิทยาพิเศษที่ประมวลผลข้อมูล ตามการประมาณค่าที่มีจำนวนมากของเซลล์ประสาทประมาณ 10 ¹¹ที่มีการเชื่อมโยงหลายประมาณ 10 15

แผนภาพ

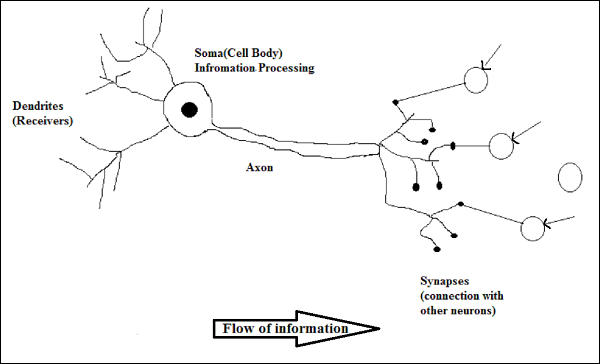
การทำงานของเซลล์ประสาททางชีวภาพ

ดังที่แสดงในแผนภาพด้านบนเซลล์ประสาททั่วไปประกอบด้วยสี่ส่วนต่อไปนี้ด้วยความช่วยเหลือซึ่งเราสามารถอธิบายการทำงานของมันได้ -

• Dendrites- เป็นกิ่งไม้คล้ายต้นไม้มีหน้าที่รับข้อมูลจากเซลล์ประสาทอื่นที่เชื่อมต่ออยู่ ในอีกแง่หนึ่งเราสามารถพูดได้ว่าพวกมันเป็นเหมือนหูของเซลล์ประสาท

• Soma - เป็นเซลล์ร่างกายของเซลล์ประสาทและมีหน้าที่ในการประมวลผลข้อมูลที่ได้รับจากเดนไดรต์

• Axon - มันเหมือนกับสายเคเบิลที่เซลล์ประสาทส่งข้อมูล

• Synapses - เป็นการเชื่อมต่อระหว่างแอกซอนและเดนไดรต์เซลล์ประสาทอื่น ๆ

ANN เทียบกับ BNN

ก่อนที่จะดูความแตกต่างระหว่าง Artificial Neural Network (ANN) และ Biological Neural Network (BNN) เรามาดูความคล้ายคลึงกันตามคำศัพท์ระหว่างสองสิ่งนี้

โครงข่ายประสาทชีวภาพ (BNN)	โครงข่ายประสาทเทียม (ANN)
โซมะ	โหนด
เดนไดรต์	อินพุต
ไซแนปส์	น้ำหนักหรือการเชื่อมต่อระหว่างกัน
แอกซอน	เอาต์พุต

ตารางต่อไปนี้แสดงการเปรียบเทียบระหว่าง ANN และ BNN ตามเกณฑ์บางประการที่กล่าวถึง

เกณฑ์	บีเอ็น	ANN
Processing	ขนานใหญ่ช้า แต่เหนือกว่า ANN	ขนานใหญ่เร็ว แต่ด้อยกว่า BNN
Size	10 11เซลล์ประสาทและ 10 15 การเชื่อมต่อระหว่างกัน	10 2ถึง 10 4โหนด (ส่วนใหญ่ขึ้นอยู่กับประเภทของแอปพลิเคชันและผู้ออกแบบเครือข่าย)
Learning	พวกเขาสามารถทนต่อความคลุมเครือ	ข้อมูลที่มีโครงสร้างและการจัดรูปแบบที่แม่นยำมากจำเป็นต้องทนต่อความคลุมเครือ
Fault tolerance	ประสิทธิภาพลดลงแม้กระทั่งความเสียหายบางส่วน	มีความสามารถในการทำงานที่แข็งแกร่งดังนั้นจึงมีศักยภาพที่จะทนต่อความผิดพลาดได้
Storage capacity	เก็บข้อมูลในไซแนปส์	เก็บข้อมูลในตำแหน่งหน่วยความจำต่อเนื่อง

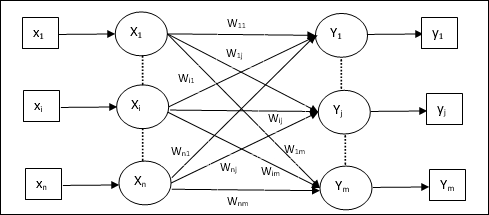
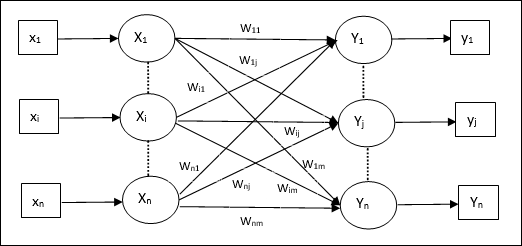
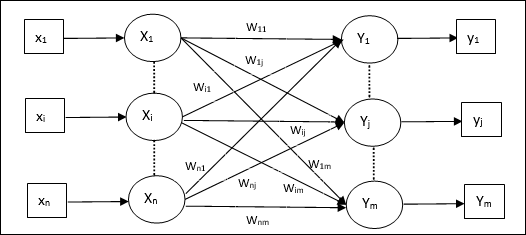
แบบจำลองโครงข่ายประสาทเทียม

แผนภาพต่อไปนี้แสดงถึงโมเดลทั่วไปของ ANN ตามด้วยการประมวลผล

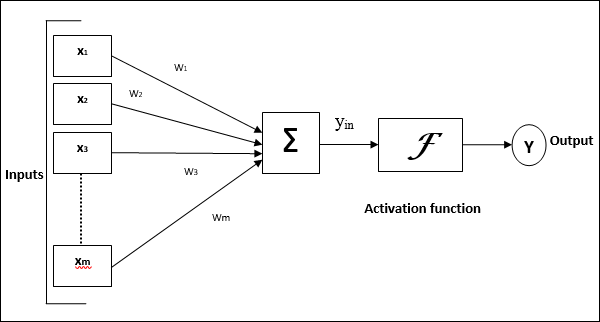
สำหรับแบบจำลองโครงข่ายประสาทเทียมทั่วไปข้างต้นสามารถคำนวณอินพุตสุทธิได้ดังนี้ -

$$ y_ {in} \: = \: x_ {1} .w_ {1} \: + \: x_ {2} .w_ {2} \: + \: x_ {3} .w_ {3} \: \ dotso \: x_ {m} .w_ {m} $$

กล่าวคืออินพุตสุทธิ $ y_ {in} \: = \: \ sum_i ^ m \: x_ {i} .w_ {i} $

ผลลัพธ์สามารถคำนวณได้โดยใช้ฟังก์ชันการเปิดใช้งานกับอินพุตสุทธิ

$$ Y \: = \: F (y_ {in}) $$

เอาท์พุท = ฟังก์ชัน (คำนวณอินพุตสุทธิ)

การประมวลผล ANN ขึ้นอยู่กับองค์ประกอบพื้นฐานสามประการต่อไปนี้ -

• โทโพโลยีเครือข่าย
• การปรับน้ำหนักหรือการเรียนรู้
• ฟังก์ชั่นการเปิดใช้งาน

ในบทนี้เราจะพูดถึงรายละเอียดเกี่ยวกับองค์ประกอบทั้งสามของ ANN

โทโพโลยีเครือข่าย

โทโพโลยีเครือข่ายคือการจัดเรียงเครือข่ายพร้อมกับโหนดและสายเชื่อมต่อ ตามโทโพโลยี ANN สามารถจัดเป็นประเภทต่อไปนี้ -

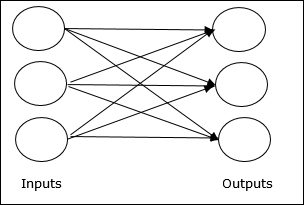
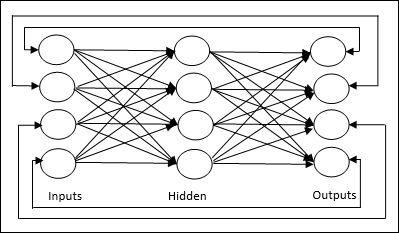
เครือข่าย Feedforward

เป็นเครือข่ายที่ไม่เกิดซ้ำที่มีหน่วยประมวลผล / โหนดในเลเยอร์และโหนดทั้งหมดในเลเยอร์เชื่อมต่อกับโหนดของเลเยอร์ก่อนหน้า การเชื่อมต่อมีน้ำหนักที่แตกต่างกัน ไม่มีลูปป้อนกลับหมายความว่าสัญญาณสามารถไหลไปในทิศทางเดียวเท่านั้นจากอินพุตไปยังเอาต์พุต อาจแบ่งออกเป็นสองประเภทดังต่อไปนี้ -

• Single layer feedforward network- แนวคิดคือ ANN feedforward ที่มีเลเยอร์ถ่วงน้ำหนักเพียงชั้นเดียว กล่าวอีกนัยหนึ่งเราสามารถพูดได้ว่าเลเยอร์อินพุตเชื่อมต่อกับเลเยอร์เอาต์พุตอย่างสมบูรณ์

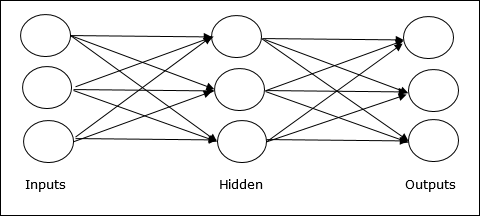
• Multilayer feedforward network- แนวคิดคือ ANN feedforward ที่มีเลเยอร์ถ่วงน้ำหนักมากกว่าหนึ่งชั้น เนื่องจากเครือข่ายนี้มีเลเยอร์อย่างน้อยหนึ่งชั้นระหว่างอินพุตและเลเยอร์เอาต์พุตจึงเรียกว่าเลเยอร์ที่ซ่อนอยู่

เครือข่ายข้อเสนอแนะ

ตามชื่อที่แนะนำเครือข่ายป้อนกลับมีเส้นทางป้อนกลับซึ่งหมายความว่าสัญญาณสามารถไหลได้ทั้งสองทิศทางโดยใช้ลูป สิ่งนี้ทำให้เป็นระบบไดนามิกที่ไม่ใช่เชิงเส้นซึ่งเปลี่ยนแปลงไปเรื่อย ๆ จนกว่าจะเข้าสู่สภาวะสมดุล อาจแบ่งออกเป็นประเภทต่างๆดังต่อไปนี้ -

• Recurrent networks- เป็นเครือข่ายข้อเสนอแนะที่มีลูปปิด ต่อไปนี้เป็นเครือข่ายที่เกิดซ้ำสองประเภท

• Fully recurrent network - เป็นสถาปัตยกรรมเครือข่ายประสาทเทียมที่ง่ายที่สุดเนื่องจากโหนดทั้งหมดเชื่อมต่อกับโหนดอื่น ๆ ทั้งหมดและแต่ละโหนดทำงานเป็นทั้งอินพุตและเอาต์พุต

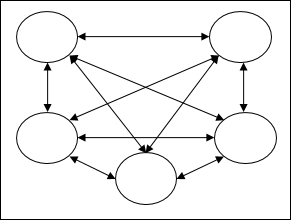
• Jordan network - เป็นเครือข่ายวงปิดซึ่งเอาต์พุตจะไปที่อินพุตอีกครั้งเป็นข้อมูลป้อนกลับดังแสดงในแผนภาพต่อไปนี้

การปรับน้ำหนักหรือการเรียนรู้

การเรียนรู้ในโครงข่ายประสาทเทียมเป็นวิธีการปรับเปลี่ยนน้ำหนักของการเชื่อมต่อระหว่างเซลล์ประสาทของเครือข่ายที่ระบุ การเรียนรู้ใน ANN สามารถแบ่งออกเป็นสามประเภท ได้แก่ การเรียนรู้ภายใต้การดูแลการเรียนรู้ที่ไม่มีผู้ดูแลและการเรียนรู้แบบเสริมกำลัง

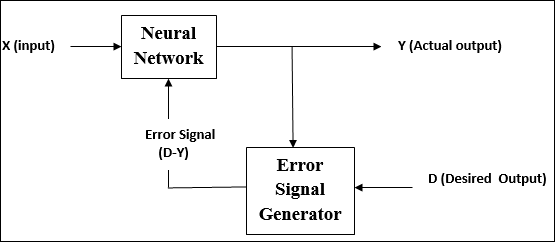
การเรียนรู้ภายใต้การดูแล

ตามชื่อการเรียนรู้ประเภทนี้ทำภายใต้การดูแลของครู กระบวนการเรียนรู้นี้ขึ้นอยู่กับ

ในระหว่างการฝึกอบรม ANN ภายใต้การเรียนรู้ภายใต้การดูแลเวกเตอร์อินพุตจะถูกนำเสนอไปยังเครือข่ายซึ่งจะให้เวกเตอร์เอาต์พุต เวกเตอร์เอาต์พุตนี้เปรียบเทียบกับเวกเตอร์เอาต์พุตที่ต้องการ สัญญาณข้อผิดพลาดจะถูกสร้างขึ้นหากมีความแตกต่างระหว่างเอาต์พุตจริงและเวกเตอร์เอาต์พุตที่ต้องการ บนพื้นฐานของสัญญาณข้อผิดพลาดนี้น้ำหนักจะถูกปรับจนกว่าเอาต์พุตจริงจะตรงกับเอาต์พุตที่ต้องการ

การเรียนรู้ที่ไม่มีผู้ดูแล

ตามชื่อการเรียนรู้ประเภทนี้ทำได้โดยไม่ต้องอยู่ภายใต้การดูแลของครู กระบวนการเรียนรู้นี้เป็นอิสระ

ในระหว่างการฝึกอบรม ANN ภายใต้การเรียนรู้ที่ไม่มีการดูแลจะรวมเวกเตอร์อินพุตประเภทที่คล้ายคลึงกันเพื่อสร้างคลัสเตอร์ เมื่อใช้รูปแบบการป้อนข้อมูลใหม่เครือข่ายประสาทจะให้การตอบสนองของเอาต์พุตที่ระบุคลาสที่เป็นรูปแบบการป้อนข้อมูล

ไม่มีข้อเสนอแนะจากสภาพแวดล้อมว่าอะไรควรเป็นผลลัพธ์ที่ต้องการและถูกต้องหรือไม่ถูกต้อง ดังนั้นในการเรียนรู้ประเภทนี้เครือข่ายจะต้องค้นพบรูปแบบและคุณสมบัติจากข้อมูลอินพุตและความสัมพันธ์ของข้อมูลอินพุตเหนือเอาต์พุต

การเรียนรู้เสริมแรง

ตามชื่อที่แนะนำการเรียนรู้ประเภทนี้ใช้เพื่อเสริมสร้างหรือเสริมสร้างเครือข่ายผ่านข้อมูลนักวิจารณ์บางอย่าง กระบวนการเรียนรู้นี้คล้ายกับการเรียนรู้ภายใต้การดูแล แต่เราอาจมีข้อมูลน้อยมาก

ในระหว่างการฝึกอบรมเครือข่ายภายใต้การเรียนรู้แบบเสริมแรงเครือข่ายจะได้รับข้อเสนอแนะจากสิ่งแวดล้อม สิ่งนี้ทำให้คล้ายกับการเรียนรู้ภายใต้การดูแล อย่างไรก็ตามข้อเสนอแนะที่ได้รับที่นี่เป็นการประเมินที่ไม่ได้ให้คำแนะนำซึ่งหมายความว่าไม่มีครูในการเรียนรู้ภายใต้การดูแล หลังจากได้รับข้อเสนอแนะเครือข่ายจะทำการปรับน้ำหนักเพื่อรับข้อมูลนักวิจารณ์ที่ดีขึ้นในอนาคต

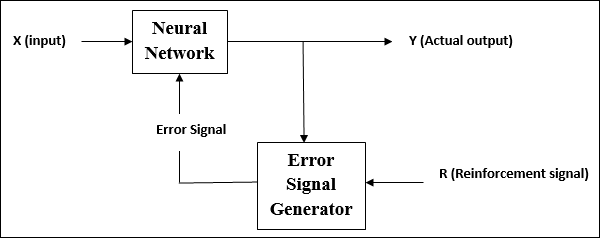
ฟังก์ชั่นการเปิดใช้งาน

อาจถูกกำหนดให้เป็นแรงพิเศษหรือความพยายามที่ใช้กับอินพุตเพื่อให้ได้เอาต์พุตที่แน่นอน ใน ANN เรายังสามารถใช้ฟังก์ชันการเปิดใช้งานกับอินพุตเพื่อให้ได้ผลลัพธ์ที่แน่นอน ต่อไปนี้เป็นฟังก์ชั่นการเปิดใช้งานที่น่าสนใจ -

ฟังก์ชันการเปิดใช้งานเชิงเส้น

เรียกอีกอย่างว่าฟังก์ชันเอกลักษณ์เนื่องจากไม่มีการแก้ไขอินพุต สามารถกำหนดเป็น -

$$ F (x) \: = \: x $$

ฟังก์ชันการเปิดใช้งาน Sigmoid

มีสองประเภทดังนี้ -

• Binary sigmoidal function- ฟังก์ชันการเปิดใช้งานนี้ทำการแก้ไขอินพุตระหว่าง 0 ถึง 1 ซึ่งเป็นค่าบวก มีขอบเขตเสมอซึ่งหมายความว่าเอาต์พุตต้องไม่น้อยกว่า 0 และมากกว่า 1 นอกจากนี้ยังเพิ่มขึ้นอย่างเคร่งครัดตามธรรมชาติซึ่งหมายความว่าอินพุตที่สูงขึ้นจะเป็นเอาต์พุต สามารถกำหนดเป็น

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$

• Bipolar sigmoidal function- ฟังก์ชันการเปิดใช้งานนี้ทำการแก้ไขอินพุตระหว่าง -1 ถึง 1 ซึ่งอาจเป็นค่าบวกหรือลบก็ได้ มีขอบเขตเสมอซึ่งหมายความว่าเอาต์พุตต้องไม่น้อยกว่า -1 และมากกว่า 1 นอกจากนี้ยังเพิ่มขึ้นอย่างเคร่งครัดในลักษณะเช่นฟังก์ชัน sigmoid สามารถกำหนดเป็น

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ frac {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$

ดังที่ระบุไว้ก่อนหน้านี้ ANN ได้รับแรงบันดาลใจอย่างสมบูรณ์จากระบบประสาททางชีววิทยานั่นคือสมองของมนุษย์ทำงาน ลักษณะที่น่าประทับใจที่สุดของสมองมนุษย์คือการเรียนรู้ด้วยเหตุนี้ ANN จึงได้มาซึ่งคุณลักษณะเดียวกัน

การเรียนรู้ใน ANN คืออะไร?

โดยพื้นฐานแล้วการเรียนรู้หมายถึงการทำและปรับตัวให้เข้ากับการเปลี่ยนแปลงในตัวของมันเองและเมื่อมีการเปลี่ยนแปลงในสิ่งแวดล้อม ANN เป็นระบบที่ซับซ้อนหรือเราสามารถพูดได้อย่างชัดเจนว่าเป็นระบบปรับตัวที่ซับซ้อนซึ่งสามารถเปลี่ยนแปลงโครงสร้างภายในได้ตามข้อมูลที่ส่งผ่าน

ทำไมมันถึงสำคัญ?

การเป็นระบบการปรับตัวที่ซับซ้อนการเรียนรู้ใน ANN หมายความว่าหน่วยประมวลผลสามารถเปลี่ยนพฤติกรรมอินพุต / เอาต์พุตได้เนื่องจากการเปลี่ยนแปลงของสภาพแวดล้อม ความสำคัญของการเรียนรู้ใน ANN เพิ่มขึ้นเนื่องจากฟังก์ชันการเปิดใช้งานคงที่เช่นเดียวกับเวกเตอร์อินพุต / เอาต์พุตเมื่อสร้างเครือข่ายเฉพาะ ตอนนี้เพื่อเปลี่ยนพฤติกรรมอินพุต / เอาต์พุตเราจำเป็นต้องปรับน้ำหนัก

การจำแนกประเภท

อาจถูกกำหนดให้เป็นกระบวนการเรียนรู้เพื่อแยกแยะข้อมูลของกลุ่มตัวอย่างออกเป็นชั้นเรียนต่างๆโดยการค้นหาคุณลักษณะทั่วไประหว่างกลุ่มตัวอย่างในชั้นเรียนเดียวกัน ตัวอย่างเช่นในการฝึกอบรม ANN เรามีตัวอย่างการฝึกอบรมที่มีคุณสมบัติเฉพาะและในการทดสอบเรามีตัวอย่างการทดสอบที่มีคุณสมบัติเฉพาะอื่น ๆ การจัดหมวดหมู่เป็นตัวอย่างของการเรียนรู้ภายใต้การดูแล

กฎการเรียนรู้ของโครงข่ายประสาทเทียม

เรารู้ว่าในระหว่างการเรียนรู้ ANN ในการเปลี่ยนพฤติกรรมอินพุต / เอาต์พุตเราจำเป็นต้องปรับน้ำหนัก ดังนั้นจึงจำเป็นต้องใช้วิธีการที่สามารถแก้ไขน้ำหนักได้ วิธีการเหล่านี้เรียกว่ากฎการเรียนรู้ซึ่งเป็นเพียงอัลกอริทึมหรือสมการ ต่อไปนี้เป็นกฎการเรียนรู้บางประการสำหรับโครงข่ายประสาทเทียม -

กฎการเรียนรู้ Hebbian

กฎนี้หนึ่งในกฎที่เก่าแก่ที่สุดและง่ายที่สุดได้รับการแนะนำโดย Donald Hebb ในหนังสือของเขาThe Organization of Behaviorในปีพ. ศ. 2492 เป็นการเรียนรู้แบบป้อนไปข้างหน้าและไม่มีการดูแล

Basic Concept - กฎนี้เป็นไปตามข้อเสนอของ Hebb ผู้เขียน -

“ เมื่อแอกซอนของเซลล์ A อยู่ใกล้มากพอที่จะกระตุ้นเซลล์ B และมีส่วนร่วมในการยิงเซลล์ B ซ้ำ ๆ หรืออย่างต่อเนื่องกระบวนการเจริญเติบโตหรือการเปลี่ยนแปลงการเผาผลาญบางอย่างจะเกิดขึ้นในเซลล์เดียวหรือทั้งสองเซลล์เช่นประสิทธิภาพของ A ในขณะที่เซลล์ใดเซลล์หนึ่งยิง B เพิ่มขึ้น”

จากสมมติฐานข้างต้นเราสามารถสรุปได้ว่าการเชื่อมต่อระหว่างเซลล์ประสาทสองเซลล์อาจแข็งแรงขึ้นหากเซลล์ประสาททำงานในเวลาเดียวกันและอาจอ่อนแอลงหากพวกมันยิงในเวลาที่ต่างกัน

Mathematical Formulation - ตามกฎการเรียนรู้ของ Hebbian ต่อไปนี้เป็นสูตรในการเพิ่มน้ำหนักของการเชื่อมต่อในทุกขั้นตอน

$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$

ที่นี่ $ \ Delta w_ {ji} (t) $ ⁡ = เพิ่มขึ้นโดยที่น้ำหนักของการเชื่อมต่อเพิ่มขึ้นในขั้นตอนเวลา t

$ \ alpha $ = อัตราการเรียนรู้เชิงบวกและคงที่

$ x_ {i} (t) $ = ค่าอินพุตจากเซลล์ประสาท pre-synaptic ในขั้นตอนเวลา t

$ y_ {i} (t) $ = ผลลัพธ์ของเซลล์ประสาท pre-synaptic ในขั้นตอนเดียวกัน t

กฎการเรียนรู้ของ Perceptron

กฎนี้เป็นข้อผิดพลาดในการแก้ไขอัลกอริธึมการเรียนรู้ภายใต้การดูแลของเครือข่ายฟีดฟอร์เวิร์ดชั้นเดียวที่มีฟังก์ชันการเปิดใช้งานเชิงเส้นซึ่งแนะนำโดย Rosenblatt

Basic Concept- ตามที่ได้รับการดูแลโดยธรรมชาติในการคำนวณข้อผิดพลาดจะมีการเปรียบเทียบระหว่างเอาต์พุตที่ต้องการ / เป้าหมายและเอาต์พุตจริง หากพบความแตกต่างจะต้องทำการเปลี่ยนแปลงน้ำหนักของการเชื่อมต่อ

Mathematical Formulation - เพื่ออธิบายการกำหนดทางคณิตศาสตร์สมมติว่าเรามีจำนวน 'n' ของเวกเตอร์อินพุต จำกัด x (n) พร้อมกับเวกเตอร์เอาต์พุตที่ต้องการ / เป้าหมาย t (n) โดยที่ n = 1 ถึง N

ตอนนี้สามารถคำนวณเอาต์พุต 'y' ได้ตามที่อธิบายไว้ก่อนหน้าบนพื้นฐานของอินพุตสุทธิและฟังก์ชันการเปิดใช้งานที่ใช้กับอินพุตสุทธินั้นสามารถแสดงได้ดังนี้ -

$$ y \: = \: f (y_ {in}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {cases} $$

ที่ไหน θ คือเกณฑ์

การอัปเดตน้ำหนักสามารถทำได้ในสองกรณีต่อไปนี้ -

Case I - เมื่อไหร่ t ≠ yแล้ว

$$ w (ใหม่) \: = \: w (เก่า) \: + \; tx $$

Case II - เมื่อไหร่ t = yแล้ว

ไม่มีการเปลี่ยนแปลงน้ำหนัก

กฎการเรียนรู้เดลต้า (กฎ Widrow-Hoff)

ได้รับการแนะนำโดย Bernard Widrow และ Marcian Hoff หรือที่เรียกว่าวิธี Least Mean Square (LMS) เพื่อลดข้อผิดพลาดในรูปแบบการฝึกอบรมทั้งหมด เป็นอัลกอริธึมการเรียนรู้ภายใต้การดูแลที่มีฟังก์ชันการเปิดใช้งานอย่างต่อเนื่อง

Basic Concept- พื้นฐานของกฎนี้คือแนวทางการไล่ระดับสีซึ่งจะดำเนินต่อไปตลอดกาล กฎเดลต้าจะอัปเดตน้ำหนักซิแนปติกเพื่อลดอินพุตสุทธิไปยังหน่วยเอาต์พุตและค่าเป้าหมาย

Mathematical Formulation - ในการอัปเดตน้ำหนัก synaptic กฎเดลต้าจะกำหนดโดย

$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$

ที่นี่ $ \ Delta w_ {i} $ = weight change for i ^th ⁡pattern;

$ \ alpha $ = อัตราการเรียนรู้เชิงบวกและคงที่

$ x_ {i} $ = ค่าอินพุตจากเซลล์ประสาท pre-synaptic;

$ e_ {j} $ = $ (t \: - \: y_ {in}) $ ความแตกต่างระหว่างผลลัพธ์ที่ต้องการ / เป้าหมายและผลลัพธ์จริง⁡ $ y_ {in} $

กฎเดลต้าข้างต้นมีไว้สำหรับหน่วยเอาต์พุตเดียวเท่านั้น

การอัปเดตน้ำหนักสามารถทำได้ในสองกรณีต่อไปนี้ -

Case-I - เมื่อไหร่ t ≠ yแล้ว

$$ w (ใหม่) \: = \: w (เก่า) \: + \: \ Delta w $$

Case-II - เมื่อไหร่ t = yแล้ว

ไม่มีการเปลี่ยนแปลงน้ำหนัก

กฎการเรียนรู้ที่แข่งขันได้ (ผู้ชนะจะได้ทั้งหมด)

เกี่ยวข้องกับการฝึกอบรมที่ไม่มีผู้ดูแลซึ่งโหนดเอาต์พุตพยายามแข่งขันกันเพื่อแสดงรูปแบบการป้อนข้อมูล เพื่อให้เข้าใจกฎการเรียนรู้นี้เราต้องเข้าใจเครือข่ายการแข่งขันซึ่งได้รับดังต่อไปนี้ -

Basic Concept of Competitive Network- เครือข่ายนี้เหมือนกับเครือข่าย feedforward แบบชั้นเดียวที่มีการเชื่อมต่อข้อมูลป้อนกลับระหว่างเอาต์พุต การเชื่อมต่อระหว่างเอาท์พุทเป็นประเภทการยับยั้งซึ่งแสดงโดยเส้นประซึ่งหมายความว่าคู่แข่งไม่เคยสนับสนุนตัวเอง

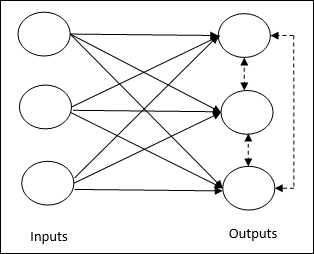
Basic Concept of Competitive Learning Rule- ดังที่กล่าวไว้ก่อนหน้านี้จะมีการแข่งขันระหว่างโหนดเอาต์พุต ดังนั้นแนวคิดหลักคือในระหว่างการฝึกอบรมหน่วยเอาต์พุตที่มีการเปิดใช้งานสูงสุดตามรูปแบบอินพุตที่กำหนดจะได้รับการประกาศให้เป็นผู้ชนะ กฎนี้เรียกอีกอย่างว่า Winner-take-all เนื่องจากมีการอัปเดตเฉพาะเซลล์ประสาทที่ชนะเท่านั้นและเซลล์ประสาทที่เหลือจะไม่เปลี่ยนแปลง

Mathematical formulation - ต่อไปนี้เป็นปัจจัยสำคัญสามประการสำหรับการกำหนดทางคณิตศาสตร์ของกฎการเรียนรู้นี้ -

• Condition to be a winner - สมมติว่าถ้าเซลล์ประสาท $ y_ {k} $ ⁡⁡อยากเป็นผู้ชนะก็จะมีเงื่อนไขดังต่อไปนี้ -

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & มิฉะนั้น \ end {cases} $$

หมายความว่าหากเซลล์ประสาทใด ๆ พูดว่า $ y_ {k} $ ⁡ต้องการที่จะชนะจากนั้นฟิลด์ท้องถิ่นที่เกิดขึ้น (ผลลัพธ์ของหน่วยการรวม) กล่าวว่า $ v_ {k} $ จะต้องมีขนาดใหญ่ที่สุดในบรรดาเซลล์ประสาทอื่น ๆ ทั้งหมด ในเครือข่าย

• Condition of sum total of weight - ข้อ จำกัด อีกประการหนึ่งของกฎการเรียนรู้เชิงแข่งขันคือผลรวมของน้ำหนักของเซลล์ประสาทขาออกเฉพาะจะเป็น 1 ตัวอย่างเช่นถ้าเราพิจารณาเซลล์ประสาท k แล้ว -

  $$ \ displaystyle \ sum \ LIMIT_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: สำหรับ \: ทั้งหมด \: k $$

• Change of weight for winner- หากเซลล์ประสาทไม่ตอบสนองต่อรูปแบบการป้อนข้อมูลจะไม่มีการเรียนรู้เกิดขึ้นในเซลล์ประสาทนั้น อย่างไรก็ตามหากเซลล์ประสาทตัวใดตัวหนึ่งชนะน้ำหนักที่เกี่ยวข้องจะถูกปรับดังต่อไปนี้

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & if \: neuron \: k \: Loss \ end {cases} $$

ที่นี่ $ \ alpha $ คืออัตราการเรียนรู้

สิ่งนี้แสดงให้เห็นอย่างชัดเจนว่าเรากำลังนิยมเซลล์ประสาทที่ชนะโดยการปรับน้ำหนักของมันและหากมีการสูญเสียเซลล์ประสาทเราก็ไม่จำเป็นต้องปรับน้ำหนักของมันใหม่

กฎการเรียนรู้ของ Outstar

กฎนี้นำเสนอโดย Grossberg เกี่ยวข้องกับการเรียนรู้ภายใต้การดูแลเนื่องจากทราบผลลัพธ์ที่ต้องการ เรียกอีกอย่างว่า Grossberg learning

Basic Concept- กฎนี้ใช้กับเซลล์ประสาทที่เรียงเป็นชั้น ๆ ได้รับการออกแบบมาเป็นพิเศษเพื่อให้ได้ผลลัพธ์ที่ต้องการd ของเลเยอร์ของ p เซลล์ประสาท.

Mathematical Formulation - การปรับน้ำหนักในกฎนี้คำนวณได้ดังนี้

$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$

ที่นี่ d คือผลลัพธ์ของเซลล์ประสาทที่ต้องการและ $ \ alpha $ คืออัตราการเรียนรู้

ตามชื่อ supervised learningเกิดขึ้นภายใต้การดูแลของครู กระบวนการเรียนรู้นี้ขึ้นอยู่กับ ในระหว่างการฝึก ANN ภายใต้การเรียนรู้ภายใต้การดูแลเวกเตอร์อินพุตจะถูกนำเสนอไปยังเครือข่ายซึ่งจะสร้างเวกเตอร์เอาต์พุต เวกเตอร์เอาต์พุตนี้เปรียบเทียบกับเวกเตอร์เอาต์พุตที่ต้องการ / เป้าหมาย สัญญาณข้อผิดพลาดจะถูกสร้างขึ้นหากมีความแตกต่างระหว่างเอาต์พุตจริงและเวกเตอร์เอาต์พุตที่ต้องการ / เป้าหมาย บนพื้นฐานของสัญญาณข้อผิดพลาดนี้น้ำหนักจะถูกปรับจนกว่าเอาต์พุตจริงจะตรงกับเอาต์พุตที่ต้องการ

เพอร์เซปตรอน

พัฒนาโดย Frank Rosenblatt โดยใช้แบบจำลอง McCulloch และ Pitts perceptron เป็นหน่วยปฏิบัติการพื้นฐานของโครงข่ายประสาทเทียม ใช้กฎการเรียนรู้ภายใต้การดูแลและสามารถจำแนกข้อมูลออกเป็นสองชั้น

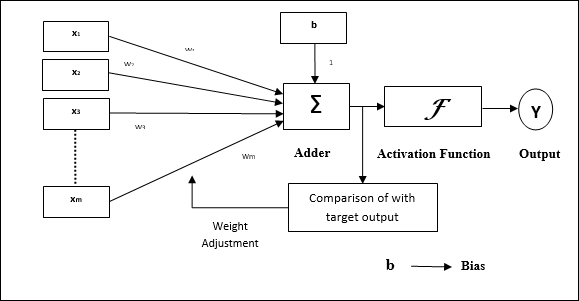
ลักษณะการทำงานของเพอร์เซปตรอน: ประกอบด้วยเซลล์ประสาทเดียวที่มีจำนวนอินพุตตามอำเภอใจพร้อมกับน้ำหนักที่ปรับได้ แต่เอาต์พุตของเซลล์ประสาทคือ 1 หรือ 0 ขึ้นอยู่กับเกณฑ์ นอกจากนี้ยังประกอบด้วยอคติที่มีน้ำหนักเสมอ 1 รูปต่อไปนี้ให้การแสดงแผนผังของเพอร์เซปตรอน

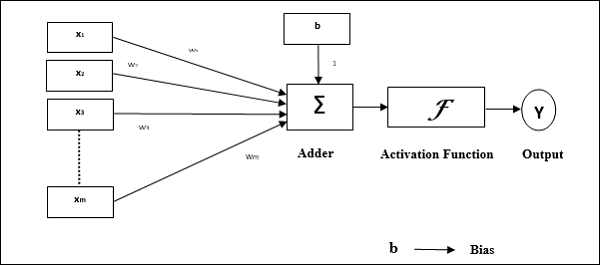
Perceptron จึงมีองค์ประกอบพื้นฐานสามประการดังต่อไปนี้ -

• Links - มันจะมีชุดของลิงค์การเชื่อมต่อซึ่งมีน้ำหนักรวมถึงอคติที่มีน้ำหนักเสมอ 1

• Adder - เพิ่มอินพุตหลังจากคูณด้วยน้ำหนักตามลำดับ

• Activation function- มัน จำกัด การส่งออกของเซลล์ประสาท ฟังก์ชันการเปิดใช้งานขั้นพื้นฐานที่สุดคือฟังก์ชันขั้นตอน Heaviside ที่มีเอาต์พุตที่เป็นไปได้สองแบบ ฟังก์ชันนี้จะคืนค่า 1 หากอินพุตเป็นบวกและ 0 สำหรับอินพุตเชิงลบใด ๆ

อัลกอริทึมการฝึกอบรม

สามารถฝึกเครือข่าย Perceptron สำหรับยูนิตเอาต์พุตเดี่ยวและยูนิตเอาต์พุตหลายยูนิต

อัลกอริทึมการฝึกอบรมสำหรับหน่วยเอาต์พุตเดี่ยว

Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• Weights
• Bias
• อัตราการเรียนรู้ $ \ alpha $

เพื่อการคำนวณที่ง่ายและเรียบง่ายต้องกำหนดน้ำหนักและอคติให้เท่ากับ 0 และต้องกำหนดอัตราการเรียนรู้ให้เท่ากับ 1

Step 2 - ทำตามขั้นตอนที่ 3-8 ต่อเมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำต่อขั้นตอนที่ 4-6 สำหรับเวกเตอร์การฝึกทุกตัว x.

Step 4 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 5 - ตอนนี้รับอินพุตสุทธิด้วยความสัมพันธ์ต่อไปนี้ -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ LIMIT_ {i} ^ n x_ {i}. \: w_ {i} $$

ที่นี่ ‘b’ เป็นอคติและ ‘n’ คือจำนวนเซลล์ประสาทอินพุตทั้งหมด

Step 6 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อรับผลลัพธ์สุดท้าย

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {cases} $$

Step 7 - ปรับน้ำหนักและอคติดังนี้ -

Case 1 - ถ้า y ≠ t จากนั้น

$$ w_ {i} (ใหม่) \: = \: w_ {i} (เก่า) \: + \: \ alpha \: tx_ {i} $$

$$ b (ใหม่) \: = \: b (เก่า) \: + \: \ alpha t $$

Case 2 - ถ้า y = t จากนั้น

$$ w_ {i} (ใหม่) \: = \: w_ {i} (เก่า) $$

$$ b (ใหม่) \: = \: b (เก่า) $$

ที่นี่ ‘y’ คือผลลัพธ์จริงและ ‘t’ คือผลลัพธ์ที่ต้องการ / เป้าหมาย

Step 8 - ทดสอบสภาพการหยุดซึ่งจะเกิดขึ้นเมื่อไม่มีการเปลี่ยนแปลงของน้ำหนัก

อัลกอริทึมการฝึกอบรมสำหรับหน่วยเอาต์พุตหลายหน่วย

แผนภาพต่อไปนี้เป็นสถาปัตยกรรมของ perceptron สำหรับเอาต์พุตหลายคลาส

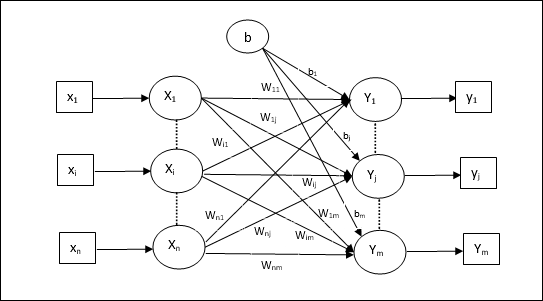
Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• Weights
• Bias
• อัตราการเรียนรู้ $ \ alpha $

เพื่อการคำนวณที่ง่ายและเรียบง่ายต้องกำหนดน้ำหนักและอคติให้เท่ากับ 0 และต้องกำหนดอัตราการเรียนรู้ให้เท่ากับ 1

Step 2 - ทำตามขั้นตอนที่ 3-8 ต่อเมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำต่อขั้นตอนที่ 4-6 สำหรับเวกเตอร์การฝึกทุกตัว x.

Step 4 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 5 - รับอินพุตสุทธิด้วยความสัมพันธ์ต่อไปนี้ -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ LIMIT_ {i} ^ n x_ {i} \: w_ {ij} $$

ที่นี่ ‘b’ เป็นอคติและ ‘n’ คือจำนวนเซลล์ประสาทอินพุตทั้งหมด

Step 6 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อรับเอาต์พุตสุดท้ายสำหรับเอาต์พุตแต่ละยูนิต j = 1 to m -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {อันตราย} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {อันตราย} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {อันตราย} \: <\: - \ theta \ end {cases} $$

Step 7 - ปรับน้ำหนักและอคติสำหรับ x = 1 to n และ j = 1 to m ดังต่อไปนี้ -

Case 1 - ถ้า y_j ≠ t_j จากนั้น

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: \ alpha \: t_ {j} x_ {i} $$

$$ b_ {j} (ใหม่) \: = \: b_ {j} (เก่า) \: + \: \ alpha t_ {j} $$

Case 2 - ถ้า y_j = t_j จากนั้น

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) $$

$$ b_ {j} (ใหม่) \: = \: b_ {j} (เก่า) $$

ที่นี่ ‘y’ คือผลลัพธ์จริงและ ‘t’ คือผลลัพธ์ที่ต้องการ / เป้าหมาย

Step 8 - ทดสอบสภาพการหยุดซึ่งจะเกิดขึ้นเมื่อไม่มีการเปลี่ยนแปลงของน้ำหนัก

เซลล์ประสาทเชิงเส้นปรับตัว (Adaline)

Adaline ซึ่งย่อมาจาก Adaptive Linear Neuron คือเครือข่ายที่มีหน่วยเชิงเส้นเดียว ได้รับการพัฒนาโดย Widrow and Hoff ในปี 1960 จุดสำคัญบางประการเกี่ยวกับ Adaline มีดังนี้ -

• ใช้ฟังก์ชันการเปิดใช้งานสองขั้ว

• ใช้กฎเดลต้าสำหรับการฝึกอบรมเพื่อลดข้อผิดพลาด Mean-Squared Error (MSE) ระหว่างเอาต์พุตจริงและเอาต์พุตที่ต้องการ / เป้าหมาย

• น้ำหนักและอคติสามารถปรับได้

สถาปัตยกรรม

โครงสร้างพื้นฐานของ Adaline นั้นคล้ายกับ perceptron ที่มีลูปข้อเสนอแนะพิเศษซึ่งจะเปรียบเทียบผลลัพธ์จริงกับเอาต์พุตที่ต้องการ / เป้าหมาย หลังจากเปรียบเทียบบนพื้นฐานของอัลกอริทึมการฝึกแล้วน้ำหนักและอคติจะได้รับการอัปเดต

อัลกอริทึมการฝึกอบรม

Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• Weights
• Bias
• อัตราการเรียนรู้ $ \ alpha $

เพื่อการคำนวณที่ง่ายและเรียบง่ายต้องกำหนดน้ำหนักและอคติให้เท่ากับ 0 และต้องกำหนดอัตราการเรียนรู้ให้เท่ากับ 1

Step 2 - ทำตามขั้นตอนที่ 3-8 ต่อเมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำขั้นตอนที่ 4-6 ต่อสำหรับคู่ฝึกไบโพลาร์ทุกคู่ s:t.

Step 4 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 5 - รับอินพุตสุทธิด้วยความสัมพันธ์ต่อไปนี้ -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ LIMIT_ {i} ^ n x_ {i} \: w_ {i} $$

ที่นี่ ‘b’ เป็นอคติและ ‘n’ คือจำนวนเซลล์ประสาทอินพุตทั้งหมด

Step 6 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อรับผลลัพธ์สุดท้าย -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {cases} $$

Step 7 - ปรับน้ำหนักและอคติดังนี้ -

Case 1 - ถ้า y ≠ t จากนั้น

$$ w_ {i} (ใหม่) \: = \: w_ {i} (เก่า) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i} $$

$$ b (ใหม่) \: = \: b (เก่า) \: + \: \ alpha (t \: - \: y_ {in}) $$

Case 2 - ถ้า y = t จากนั้น

$$ w_ {i} (ใหม่) \: = \: w_ {i} (เก่า) $$

$$ b (ใหม่) \: = \: b (เก่า) $$

ที่นี่ ‘y’ คือผลลัพธ์จริงและ ‘t’ คือผลลัพธ์ที่ต้องการ / เป้าหมาย

$ (t \: - \; y_ {in}) $ คือข้อผิดพลาดในการคำนวณ

Step 8 - ทดสอบสภาพการหยุดซึ่งจะเกิดขึ้นเมื่อไม่มีการเปลี่ยนแปลงของน้ำหนักหรือการเปลี่ยนแปลงของน้ำหนักสูงสุดที่เกิดขึ้นระหว่างการฝึกซ้อมมีค่าน้อยกว่าค่าเผื่อที่กำหนด

เซลล์ประสาทเชิงเส้นปรับตัวหลายตัว (Madaline)

Madaline ซึ่งย่อมาจาก Multiple Adaptive Linear Neuron เป็นเครือข่ายที่ประกอบด้วย Adalines จำนวนมากควบคู่กัน มันจะมีหน่วยเอาท์พุตเดียว ประเด็นสำคัญบางประการเกี่ยวกับ Madaline มีดังนี้ -

• มันเหมือนกับ Perceptron หลายชั้นโดยที่ Adaline จะทำหน้าที่เป็นหน่วยที่ซ่อนอยู่ระหว่างอินพุตและเลเยอร์ Madaline

• น้ำหนักและความลำเอียงระหว่างชั้นอินพุตและชั้นอะดาไลน์ตามที่เราเห็นในสถาปัตยกรรม Adaline สามารถปรับได้

• ชั้น Adaline และ Madaline มีน้ำหนักและอคติคงที่เท่ากับ 1

• การฝึกอบรมสามารถทำได้ด้วยความช่วยเหลือของกฎเดลต้า

สถาปัตยกรรม

สถาปัตยกรรมของ Madaline ประกอบด้วย “n” เซลล์ประสาทของชั้นอินพุต “m”เซลล์ประสาทของชั้น Adaline และ 1 เซลล์ประสาทของชั้น Madaline ชั้น Adaline ถือได้ว่าเป็นชั้นที่ซ่อนอยู่เนื่องจากอยู่ระหว่างชั้นอินพุตและชั้นเอาต์พุตนั่นคือชั้น Madaline

อัลกอริทึมการฝึกอบรม

ถึงตอนนี้เรารู้แล้วว่าต้องปรับเฉพาะน้ำหนักและอคติระหว่างชั้นอินพุตและชั้นอะดาลีนและน้ำหนักและอคติระหว่างชั้นอะดาลีนและชั้นมาดาไลน์ได้รับการแก้ไข

Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• Weights
• Bias
• อัตราการเรียนรู้ $ \ alpha $

เพื่อการคำนวณที่ง่ายและเรียบง่ายต้องกำหนดน้ำหนักและอคติให้เท่ากับ 0 และต้องกำหนดอัตราการเรียนรู้ให้เท่ากับ 1

Step 2 - ทำตามขั้นตอนที่ 3-8 ต่อเมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำขั้นตอนที่ 4-6 ต่อสำหรับคู่ฝึกไบโพลาร์ทุกคู่ s:t.

Step 4 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 5 - รับอินพุตสุทธิในแต่ละชั้นที่ซ่อนอยู่นั่นคือชั้น Adaline ที่มีความสัมพันธ์ดังต่อไปนี้ -

$$ Q_ {อันตราย} \: = \: b_ {j} \: + \: \ displaystyle \ sum \ LIMIT_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: ถึง \: m $$

ที่นี่ ‘b’ เป็นอคติและ ‘n’ คือจำนวนเซลล์ประสาทอินพุตทั้งหมด

Step 6 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อให้ได้ผลลัพธ์สุดท้ายที่ชั้น Adaline และชั้น Madaline -

$$ f (x) \: = \: \ begin {cases} 1 & if \: x \: \ geqslant \: 0 \\ - 1 & if \: x \: <\: 0 \ end {cases} $ $

เอาท์พุทที่หน่วย (Adaline) ที่ซ่อนอยู่

$$ Q_ {j} \: = \: f (Q_ {อันตราย}) $$

ผลลัพธ์สุดท้ายของเครือข่าย

$$ y \: = \: f (y_ {in}) $$

i.e. $ \: \: y_ {อันตราย} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j} $

Step 7 - คำนวณข้อผิดพลาดและปรับน้ำหนักดังนี้ -

Case 1 - ถ้า y ≠ t และ t = 1 จากนั้น

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: \ alpha (1 \: - \: Q_ {อันตราย}) x_ {i} $$

$$ b_ {j} (ใหม่) \: = \: b_ {j} (เก่า) \: + \: \ alpha (1 \: - \: Q_ {อันตราย}) $$

ในกรณีนี้น้ำหนักจะได้รับการอัปเดตเมื่อ Q_j โดยที่อินพุตสุทธิใกล้เคียงกับ 0 เนื่องจาก t = 1.

Case 2 - ถ้า y ≠ t และ t = -1 จากนั้น

$$ w_ {ik} (ใหม่) \: = \: w_ {ik} (เก่า) \: + \: \ alpha (-1 \: - \: Q_ {ink}) x_ {i} $$

$$ b_ {k} (ใหม่) \: = \: b_ {k} (เก่า) \: + \: \ alpha (-1 \: - \: Q_ {ink}) $$

ในกรณีนี้น้ำหนักจะได้รับการอัปเดตเมื่อ Q_k โดยที่อินพุตสุทธิเป็นบวกเพราะ t = -1.

ที่นี่ ‘y’ คือผลลัพธ์จริงและ ‘t’ คือผลลัพธ์ที่ต้องการ / เป้าหมาย

Case 3 - ถ้า y = t แล้ว

น้ำหนักจะไม่มีการเปลี่ยนแปลง

Step 8 - ทดสอบสภาพการหยุดซึ่งจะเกิดขึ้นเมื่อไม่มีการเปลี่ยนแปลงของน้ำหนักหรือการเปลี่ยนแปลงของน้ำหนักสูงสุดที่เกิดขึ้นระหว่างการฝึกซ้อมมีค่าน้อยกว่าค่าเผื่อที่กำหนด

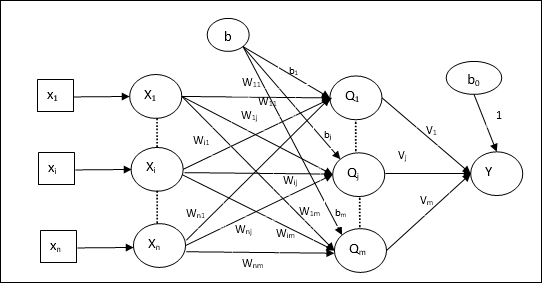
ย้อนกลับเครือข่ายประสาทการแพร่กระจาย

Back Propagation Neural (BPN) คือโครงข่ายประสาทเทียมหลายชั้นซึ่งประกอบด้วยชั้นอินพุตชั้นที่ซ่อนอยู่และเลเยอร์เอาต์พุตอย่างน้อยหนึ่งชั้น ตามชื่อของมันการเผยแพร่ย้อนกลับจะเกิดขึ้นในเครือข่ายนี้ ข้อผิดพลาดซึ่งคำนวณที่เลเยอร์เอาต์พุตโดยการเปรียบเทียบเอาต์พุตเป้าหมายและเอาต์พุตจริงจะถูกส่งกลับไปยังเลเยอร์อินพุต

สถาปัตยกรรม

ดังที่แสดงในแผนภาพสถาปัตยกรรมของ BPN มีสามชั้นที่เชื่อมต่อกันซึ่งมีน้ำหนักอยู่ เลเยอร์ที่ซ่อนอยู่และเลเยอร์เอาต์พุตยังมีอคติซึ่งมีน้ำหนักเท่ากับ 1 เสมอ ดังที่เห็นได้ชัดจากแผนภาพการทำงานของ BPN มีสองขั้นตอน เฟสหนึ่งส่งสัญญาณจากชั้นอินพุตไปยังชั้นเอาต์พุตและอีกเฟสกลับเผยแพร่ข้อผิดพลาดจากชั้นเอาต์พุตไปยังชั้นอินพุต

อัลกอริทึมการฝึกอบรม

สำหรับการฝึกอบรม BPN จะใช้ฟังก์ชันการเปิดใช้งานไบนารีซิกมอยด์ การฝึกอบรมของ BPN จะมีสามขั้นตอนดังต่อไปนี้

• Phase 1 - ฟีดไปข้างหน้าเฟส

• Phase 2 - กลับเผยแพร่ข้อผิดพลาด

• Phase 3 - อัปเดตน้ำหนัก

ขั้นตอนทั้งหมดนี้จะสรุปได้ในอัลกอริทึมดังนี้

Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• Weights
• อัตราการเรียนรู้ $ \ alpha $

สำหรับการคำนวณที่ง่ายและเรียบง่ายให้ใช้ค่าสุ่มเล็ก ๆ

Step 2 - ทำต่อขั้นตอนที่ 3-11 เมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำขั้นตอนที่ 4-10 ต่อทุกคู่การฝึก

ขั้นตอนที่ 1

Step 4 - หน่วยอินพุตแต่ละหน่วยรับสัญญาณอินพุต x_i และส่งไปยังหน่วยที่ซ่อนอยู่สำหรับทุกคน i = 1 to n

Step 5 - คำนวณอินพุตสุทธิที่หน่วยที่ซ่อนอยู่โดยใช้ความสัมพันธ์ต่อไปนี้ -

$$ Q_ {อันตราย} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: j \: = \ : 1 \: ถึง \: p $$

ที่นี่ b_0j คืออคติของหน่วยที่ซ่อนอยู่ v_ij น้ำหนักอยู่ที่ j หน่วยของเลเยอร์ที่ซ่อนอยู่มาจาก i หน่วยของชั้นอินพุต

ตอนนี้คำนวณผลลัพธ์สุทธิโดยใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้

$$ Q_ {j} \: = \: f (Q_ {อันตราย}) $$

ส่งสัญญาณเอาต์พุตเหล่านี้ของยูนิตเลเยอร์ที่ซ่อนอยู่ไปยังยูนิตเลเยอร์เอาต์พุต

Step 6 - คำนวณอินพุตสุทธิที่หน่วยชั้นเอาต์พุตโดยใช้ความสัมพันธ์ต่อไปนี้ -

$$ y_ {ink} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: ถึง \: m $$

ที่นี่ b_0k ⁡เป็นอคติของหน่วยเอาท์พุท w_jk น้ำหนักอยู่ที่ k หน่วยของชั้นเอาต์พุตที่มาจาก j หน่วยของชั้นที่ซ่อนอยู่

คำนวณผลลัพธ์สุทธิโดยใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้

$$ y_ {k} \: = \: f (y_ {ink}) $$

ระยะที่ 2

Step 7 - คำนวณระยะการแก้ไขข้อผิดพลาดให้สอดคล้องกับรูปแบบเป้าหมายที่ได้รับในแต่ละหน่วยเอาต์พุตดังนี้ -

$$ \ delta_ {k} \: = \ :( t_ {k} \: - \: y_ {k}) f ^ {'} (y_ {ink}) $$

บนพื้นฐานนี้ให้อัปเดตน้ำหนักและอคติดังนี้ -

$$ \ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij} $$

$$ \ Delta b_ {0k} \: = \: \ alpha \ delta_ {k} $$

จากนั้นส่ง $ \ delta_ {k} $ กลับไปที่เลเยอร์ที่ซ่อนอยู่

Step 8 - ตอนนี้แต่ละหน่วยที่ซ่อนอยู่จะเป็นผลรวมของอินพุตเดลต้าจากหน่วยเอาต์พุต

$$ \ delta_ {อันตราย} \: = \: \ displaystyle \ sum \ LIMIT_ {k = 1} ^ m \ delta_ {k} \: w_ {jk} $$

สามารถคำนวณระยะผิดพลาดได้ดังนี้ -

$$ \ delta_ {j} \: = \: \ delta_ {อันตราย} f ^ {'} (Q_ {อันตราย}) $$

บนพื้นฐานนี้ให้อัปเดตน้ำหนักและอคติดังนี้ -

$$ \ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i} $$

$$ \ Delta b_ {0j} \: = \: \ alpha \ delta_ {j} $$

ระยะที่ 3

Step 9 - แต่ละหน่วยเอาต์พุต (y_kk = 1 to m) ปรับปรุงน้ำหนักและอคติดังนี้ -

$$ v_ {jk} (ใหม่) \: = \: v_ {jk} (เก่า) \: + \: \ Delta v_ {jk} $$

$$ b_ {0k} (ใหม่) \: = \: b_ {0k} (เก่า) \: + \: \ Delta b_ {0k} $$

Step 10 - แต่ละหน่วยเอาต์พุต (z_jj = 1 to p) ปรับปรุงน้ำหนักและอคติดังนี้ -

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: \ Delta w_ {ij} $$

$$ b_ {0j} (ใหม่) \: = \: b_ {0j} (เก่า) \: + \: \ Delta b_ {0j} $$

Step 11 - ตรวจสอบเงื่อนไขการหยุดซึ่งอาจเป็นได้ทั้งจำนวนยุคที่ถึงหรือผลลัพธ์เป้าหมายตรงกับผลลัพธ์จริง

กฎการเรียนรู้ทั่วไปของ Delta

กฎเดลต้าใช้งานได้กับเลเยอร์เอาต์พุตเท่านั้น ในทางกลับกันกฎเดลต้าทั่วไปเรียกอีกอย่างว่าback-propagation กฎคือวิธีการสร้างค่าที่ต้องการของเลเยอร์ที่ซ่อนอยู่

การกำหนดทางคณิตศาสตร์

สำหรับฟังก์ชั่นการเปิดใช้งาน $ y_ {k} \: = \: f (y_ {ink}) $ การมาของอินพุตสุทธิบนเลเยอร์ที่ซ่อนอยู่และในชั้นเอาต์พุตสามารถกำหนดได้โดย

$$ y_ {ink} \: = \: \ displaystyle \ sum \ LIMIT_i \: z_ {i} w_ {jk} $$

และ $ \: \: y_ {อันตราย} \: = \: \ sum_i x_ {i} v_ {ij} $

ตอนนี้ข้อผิดพลาดที่ต้องย่อให้เล็กที่สุดคือ

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2 $$

โดยใช้กฎลูกโซ่เรามี

$$ \ frac {\ partial E} {\ partial w_ {jk}} \: = \: \ frac {\ partial} {\ partial w_ {jk}} (\ frac {1} {2} \ displaystyle \ sum \ Limit_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2) $$

$$ = \: \ frac {\ partial} {\ partial w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {ink})] ^ 2 \ rgroup $$

$$ = \: - [t_ {k} \: - \: y_ {k}] \ frac {\ partial} {\ partial w_ {jk}} f (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f (y_ {ink}) \ frac {\ partial} {\ partial w_ {jk}} (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) z_ {j} $$

ตอนนี้ให้เราพูดว่า $ \ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) $

น้ำหนักในการเชื่อมต่อกับหน่วยที่ซ่อนอยู่ z_j ได้โดย -

$$ \ frac {\ partial E} {\ partial v_ {ij}} \: = \: - \ displaystyle \ sum \ LIMIT_ {k} \ delta_ {k} \ frac {\ partial} {\ partial v_ {ij} } \ :( y_ {ink}) $$

ใส่ค่า $ y_ {ink} $ เราจะได้สิ่งต่อไปนี้

$$ \ delta_ {j} \: = \: - \ displaystyle \ sum \ LIMIT_ {k} \ delta_ {k} w_ {jk} f ^ {'} (z_ {อันตราย}) $$

การอัปเดตน้ำหนักสามารถทำได้ดังนี้ -

สำหรับหน่วยเอาต์พุต -

$$ \ Delta w_ {jk} \: = \: - \ alpha \ frac {\ partial E} {\ partial w_ {jk}} $$

$$ = \: \ alpha \: \ delta_ {k} \: z_ {j} $$

สำหรับยูนิตที่ซ่อนอยู่ -

$$ \ Delta v_ {ij} \: = \: - \ alpha \ frac {\ partial E} {\ partial v_ {ij}} $$

$$ = \: \ alpha \: \ delta_ {j} \: x_ {i} $$

ตามชื่อการเรียนรู้ประเภทนี้ทำได้โดยไม่ต้องอยู่ภายใต้การดูแลของครู กระบวนการเรียนรู้นี้เป็นอิสระ ในระหว่างการฝึกอบรม ANN ภายใต้การเรียนรู้ที่ไม่มีการดูแลจะรวมเวกเตอร์อินพุตประเภทที่คล้ายคลึงกันเพื่อสร้างคลัสเตอร์ เมื่อมีการใช้รูปแบบการป้อนข้อมูลใหม่เครือข่ายประสาทจะให้การตอบสนองเอาต์พุตที่ระบุคลาสที่เป็นรูปแบบอินพุต ในนี้จะไม่มีข้อเสนอแนะจากสภาพแวดล้อมว่าอะไรควรเป็นผลลัพธ์ที่ต้องการและมันถูกต้องหรือไม่ถูกต้อง ดังนั้นในการเรียนรู้ประเภทนี้เครือข่ายจะต้องค้นพบรูปแบบคุณสมบัติจากข้อมูลอินพุตและความสัมพันธ์ของข้อมูลอินพุตผ่านเอาต์พุต

ผู้ชนะ - รับ - เครือข่ายทั้งหมด

เครือข่ายประเภทนี้ตั้งอยู่บนกฎการเรียนรู้ที่แข่งขันกันและจะใช้กลยุทธ์ที่มันเลือกเซลล์ประสาทที่มีอินพุตรวมมากที่สุดเป็นผู้ชนะ การเชื่อมต่อระหว่างเซลล์ประสาทเอาต์พุตแสดงการแข่งขันระหว่างพวกมันและหนึ่งในนั้นจะเป็น 'เปิด' ซึ่งหมายความว่าจะเป็นผู้ชนะและอื่น ๆ จะเป็น 'ปิด'

ต่อไปนี้เป็นเครือข่ายบางส่วนที่ใช้แนวคิดง่ายๆนี้โดยใช้การเรียนรู้ที่ไม่มีผู้ดูแล

Hamming Network

ในโครงข่ายประสาทเทียมส่วนใหญ่ใช้การเรียนรู้ที่ไม่มีผู้ดูแลจำเป็นอย่างยิ่งที่จะต้องคำนวณระยะทางและทำการเปรียบเทียบ เครือข่ายประเภทนี้คือเครือข่าย Hamming ซึ่งสำหรับเวกเตอร์อินพุตที่กำหนดทุกตัวจะรวมกลุ่มกันเป็นกลุ่มต่างๆ ต่อไปนี้เป็นคุณสมบัติที่สำคัญบางประการของ Hamming Networks -

• Lippmann เริ่มทำงานกับเครือข่าย Hamming ในปี 1987

• มันเป็นเครือข่ายชั้นเดียว

• อินพุตอาจเป็นไบนารี {0, 1} ของไบโพลาร์ {-1, 1} ก็ได้

• น้ำหนักของตาข่ายคำนวณโดยเวกเตอร์ตัวอย่าง

• เป็นโครงข่ายน้ำหนักคงที่ซึ่งหมายความว่าน้ำหนักจะยังคงเหมือนเดิมแม้ในระหว่างการฝึก

สุทธิสูงสุด

นอกจากนี้ยังเป็นเครือข่ายน้ำหนักคงที่ซึ่งทำหน้าที่เป็นเครือข่ายย่อยสำหรับการเลือกโหนดที่มีอินพุตสูงสุด โหนดทั้งหมดเชื่อมต่อกันอย่างสมบูรณ์และมีน้ำหนักสมมาตรอยู่ในการเชื่อมต่อระหว่างกันแบบถ่วงน้ำหนักทั้งหมดเหล่านี้

สถาปัตยกรรม

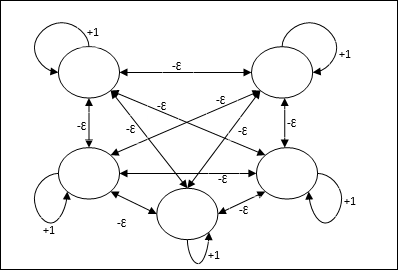
ใช้กลไกซึ่งเป็นกระบวนการซ้ำและแต่ละโหนดจะรับอินพุตยับยั้งจากโหนดอื่น ๆ ทั้งหมดผ่านการเชื่อมต่อ โหนดเดียวที่มีค่าสูงสุดจะใช้งานได้หรือเป็นผู้ชนะและการเปิดใช้งานของโหนดอื่น ๆ ทั้งหมดจะไม่ทำงาน Max Net ใช้ฟังก์ชันการเปิดใช้งานข้อมูลประจำตัวด้วย $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {cases} $$

ภารกิจของตาข่ายนี้ทำได้โดยน้ำหนักกระตุ้นตัวเองที่ +1 และขนาดการยับยั้งซึ่งกันและกันซึ่งกำหนดไว้เช่น [0 <ɛ <$ \ frac {1} {m} $] โดยที่ “m” คือจำนวนโหนดทั้งหมด

การเรียนรู้เชิงแข่งขันใน ANN

เกี่ยวข้องกับการฝึกอบรมที่ไม่มีผู้ดูแลซึ่งโหนดเอาต์พุตพยายามแข่งขันกันเพื่อแสดงรูปแบบการป้อนข้อมูล เพื่อให้เข้าใจกฎการเรียนรู้นี้เราจะต้องทำความเข้าใจเกี่ยวกับการแข่งขันซึ่งอธิบายได้ดังนี้ -

แนวคิดพื้นฐานของเครือข่ายการแข่งขัน

เครือข่ายนี้เหมือนกับเครือข่ายฟีดฟอร์เวิร์ดชั้นเดียวที่มีการเชื่อมต่อข้อมูลป้อนกลับระหว่างเอาต์พุต การเชื่อมต่อระหว่างเอาต์พุตเป็นประเภทการยับยั้งซึ่งแสดงโดยเส้นประซึ่งหมายความว่าคู่แข่งไม่เคยสนับสนุนตัวเอง

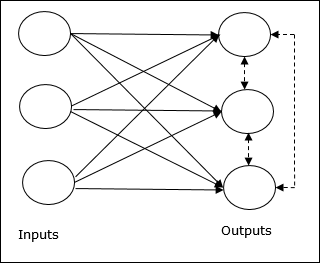
แนวคิดพื้นฐานของกฎการเรียนรู้เชิงแข่งขัน

ดังที่กล่าวไว้ก่อนหน้านี้จะมีการแข่งขันระหว่างโหนดเอาต์พุตดังนั้นแนวคิดหลักคือ - ระหว่างการฝึกอบรมหน่วยเอาต์พุตที่มีการเปิดใช้งานสูงสุดสำหรับรูปแบบอินพุตที่กำหนดจะได้รับการประกาศให้เป็นผู้ชนะ กฎนี้เรียกอีกอย่างว่า Winner-take-all เนื่องจากมีการอัปเดตเฉพาะเซลล์ประสาทที่ชนะเท่านั้นและเซลล์ประสาทที่เหลือจะไม่เปลี่ยนแปลง

การกำหนดทางคณิตศาสตร์

ต่อไปนี้เป็นปัจจัยสำคัญสามประการสำหรับการกำหนดทางคณิตศาสตร์ของกฎการเรียนรู้นี้ -

• เงื่อนไขที่จะเป็นผู้ชนะ

  สมมติว่าถ้าเซลล์ประสาท y_k ต้องการเป็นผู้ชนะก็จะมีเงื่อนไขดังต่อไปนี้

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 & มิฉะนั้น \ end {cases} $$

  หมายความว่าถ้าเซลล์ประสาทใด ๆ พูดว่า y_k ต้องการที่จะชนะจากนั้นฟิลด์ท้องถิ่นที่เกิดขึ้น (ผลลัพธ์ของหน่วยผลรวม) พูด v_kต้องมีขนาดใหญ่ที่สุดในบรรดาเซลล์ประสาทอื่น ๆ ในเครือข่าย

• เงื่อนไขของผลรวมของน้ำหนัก

  ข้อ จำกัด อีกประการหนึ่งของกฎการเรียนรู้แบบแข่งขันคือผลรวมของน้ำหนักของเซลล์ประสาทเอาท์พุตเฉพาะจะเท่ากับ 1 ตัวอย่างเช่นถ้าเราพิจารณาเซลล์ประสาท k แล้ว

  $$ \ displaystyle \ sum \ LIMIT_ {k} w_ {kj} \: = \: 1 \: \: \: \: สำหรับ \: ทั้งหมด \: \: k $$

• การเปลี่ยนแปลงน้ำหนักสำหรับผู้ชนะ

  หากเซลล์ประสาทไม่ตอบสนองต่อรูปแบบการป้อนข้อมูลจะไม่มีการเรียนรู้เกิดขึ้นในเซลล์ประสาทนั้น อย่างไรก็ตามหากเซลล์ประสาทตัวใดตัวหนึ่งชนะน้ำหนักที่เกี่ยวข้องจะถูกปรับดังนี้ -

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0 & if \: neuron \: k \: Loss \ end {cases} $$

  ที่นี่ $ \ alpha $ คืออัตราการเรียนรู้

  สิ่งนี้แสดงให้เห็นอย่างชัดเจนว่าเราให้ความสำคัญกับเซลล์ประสาทที่ชนะโดยการปรับน้ำหนักของมันและหากเซลล์ประสาทสูญเสียไปเราก็ไม่จำเป็นต้องปรับน้ำหนักของมันใหม่

K-mean Clustering Algorithm

K-mean เป็นหนึ่งในอัลกอริทึมการทำคลัสเตอร์ที่ได้รับความนิยมมากที่สุดซึ่งเราใช้แนวคิดของขั้นตอนการแบ่งพาร์ติชัน เราเริ่มต้นด้วยพาร์ติชันเริ่มต้นและย้ายรูปแบบจากคลัสเตอร์หนึ่งไปยังอีกคลัสเตอร์ซ้ำ ๆ จนกว่าเราจะได้ผลลัพธ์ที่น่าพอใจ

อัลกอริทึม

Step 1 - เลือก kจุดเป็นเซนทรอยด์เริ่มต้น เริ่มต้นk ต้นแบบ (w₁,…,w_k)ตัวอย่างเช่นเราสามารถระบุได้ด้วยเวกเตอร์อินพุตที่เลือกแบบสุ่ม -

$$ W_ {j} \: = \: i_ {p}, \: \: \: โดยที่ \: j \: \ in \ lbrace1, .... , k \ rbrace \: และ \: p \: \ ใน \ lbrace1, .... , n \ rbrace $$

แต่ละคลัสเตอร์ C_j เกี่ยวข้องกับต้นแบบ w_j.

Step 2 - ทำซ้ำขั้นตอนที่ 3-5 จนกว่า E จะไม่ลดลงอีกต่อไปมิฉะนั้นการเป็นสมาชิกคลัสเตอร์จะไม่เปลี่ยนแปลงอีกต่อไป

Step 3 - สำหรับเวกเตอร์อินพุตแต่ละรายการ i_p ที่ไหน p ∈ {1,…,n}ใส่ i_p ในคลัสเตอร์ C_j* ด้วยต้นแบบที่ใกล้ที่สุด w_j* มีความสัมพันธ์ดังต่อไปนี้

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, .... , k \ rbrace $$

Step 4 - สำหรับแต่ละคลัสเตอร์ C_j, ที่ไหน j ∈ { 1,…,k}ปรับปรุงต้นแบบ w_j เป็นเซนทรอยด์ของตัวอย่างทั้งหมดในปัจจุบัน C_j , ดังนั้น

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - คำนวณข้อผิดพลาดเชิงปริมาณทั้งหมดดังนี้ -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

นีโอโกนิตรอน

เป็นเครือข่ายฟีดฟอร์เวิร์ดหลายชั้นซึ่งพัฒนาโดย Fukushima ในปี 1980 โมเดลนี้ใช้การเรียนรู้ภายใต้การดูแลและใช้สำหรับการจดจำรูปแบบภาพซึ่งส่วนใหญ่เป็นอักขระที่เขียนด้วยมือ โดยพื้นฐานแล้วเป็นส่วนขยายของเครือข่าย Cognitron ซึ่งได้รับการพัฒนาโดย Fukushima ในปีพ. ศ. 2518

สถาปัตยกรรม

เป็นเครือข่ายแบบลำดับชั้นซึ่งประกอบด้วยหลายชั้นและมีรูปแบบการเชื่อมต่อภายในในเลเยอร์เหล่านั้น

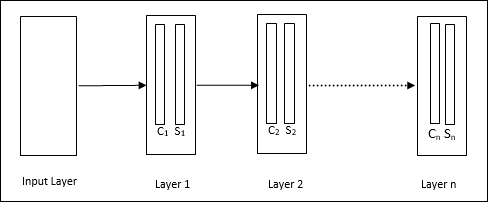
ดังที่เราได้เห็นในแผนภาพด้านบน neocognitron ถูกแบ่งออกเป็นชั้นต่างๆที่เชื่อมต่อกันและแต่ละชั้นมีสองเซลล์ คำอธิบายของเซลล์เหล่านี้มีดังนี้ -

S-Cell - เรียกว่าเซลล์ธรรมดาซึ่งได้รับการฝึกฝนให้ตอบสนองต่อรูปแบบเฉพาะหรือกลุ่มของรูปแบบ

C-Cell- เรียกว่าเซลล์ที่ซับซ้อนซึ่งรวมเอาผลลัพธ์จากเซลล์ S เข้าด้วยกันและลดจำนวนหน่วยในแต่ละอาร์เรย์ ในอีกแง่หนึ่ง C-cell แทนที่ผลลัพธ์ของ S-cell

อัลกอริทึมการฝึกอบรม

การฝึกของ neocognitron พบว่ามีความก้าวหน้าทีละชั้น น้ำหนักจากชั้นอินพุตไปยังชั้นแรกได้รับการฝึกฝนและแช่แข็ง จากนั้นน้ำหนักจากชั้นแรกถึงชั้นที่สองจะได้รับการฝึกฝนและอื่น ๆ การคำนวณภายในระหว่าง S-cell และ Ccell ขึ้นอยู่กับน้ำหนักที่มาจากชั้นก่อนหน้า ดังนั้นเราสามารถพูดได้ว่าอัลกอริทึมการฝึกขึ้นอยู่กับการคำนวณของ S-cell และ C-cell

การคำนวณใน S-cell

เซลล์ S มีสัญญาณกระตุ้นที่ได้รับจากชั้นก่อนหน้าและมีสัญญาณยับยั้งที่ได้รับภายในชั้นเดียวกัน

$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$

ที่นี่ t_i คือน้ำหนักคงที่และ c_i คือผลลัพธ์จากเซลล์ C

อินพุตที่ปรับขนาดของ S-cell สามารถคำนวณได้ดังนี้ -

$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$

ที่นี่ $ e \: = \: \ sum_i c_ {i} w_ {i} $

w_i คือน้ำหนักที่ปรับจาก C-cell เป็น S-cell

w₀ คือน้ำหนักที่ปรับได้ระหว่างอินพุตและเซลล์ S

v เป็นอินพุตกระตุ้นจากเซลล์ C

การเปิดใช้งานสัญญาณเอาต์พุตคือ

$$ s \: = \: \ begin {cases} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {cases} $$

การคำนวณในเซลล์ C

อินพุตสุทธิของ C-layer คือ

$$ C \: = \: \ displaystyle \ sum \ LIMIT_i s_ {i} x_ {i} $$

ที่นี่ s_i คือเอาต์พุตจาก S-cell และ x_i คือน้ำหนักคงที่จาก S-cell ถึง C-cell

ผลลัพธ์สุดท้ายมีดังนี้ -

$$ C_ {out} \: = \: \ begin {cases} \ frac {C} {a + C}, & if \: C> 0 \\ 0, & else \ end {cases} $$

ที่นี่ ‘a’ คือพารามิเตอร์ที่ขึ้นอยู่กับประสิทธิภาพของเครือข่าย

Learning Vector Quantization (LVQ) ซึ่งแตกต่างจาก Vector quantization (VQ) และ Kohonen Self-Organizing Maps (KSOM) โดยพื้นฐานแล้วเป็นเครือข่ายการแข่งขันที่ใช้การเรียนรู้ภายใต้การดูแล เราอาจกำหนดให้เป็นกระบวนการในการจำแนกรูปแบบโดยที่แต่ละหน่วยเอาต์พุตแสดงถึงคลาส เมื่อใช้การเรียนรู้ภายใต้การดูแลเครือข่ายจะได้รับชุดของรูปแบบการฝึกอบรมที่มีการจำแนกประเภทที่รู้จักพร้อมกับการกระจายเริ่มต้นของคลาสเอาต์พุต หลังจากเสร็จสิ้นขั้นตอนการฝึก LVQ จะจำแนกเวกเตอร์อินพุตโดยกำหนดให้เป็นคลาสเดียวกับของหน่วยเอาต์พุต

สถาปัตยกรรม

รูปต่อไปนี้แสดงสถาปัตยกรรมของ LVQ ซึ่งค่อนข้างคล้ายกับสถาปัตยกรรมของ KSOM อย่างที่เราเห็นก็มี“n” จำนวนหน่วยอินพุตและ “m”จำนวนหน่วยเอาต์พุต เลเยอร์มีการเชื่อมต่อกันอย่างเต็มที่โดยมีน้ำหนักอยู่

พารามิเตอร์ที่ใช้

ต่อไปนี้เป็นพารามิเตอร์ที่ใช้ในกระบวนการฝึกอบรม LVQ รวมทั้งในผังงาน

• x= เวกเตอร์การฝึก (x ₁ , ... , x _i , ... , x _n )

• T = คลาสสำหรับเวกเตอร์การฝึกอบรม x

• w_j = เวกเตอร์น้ำหนักสำหรับ j^th หน่วยเอาต์พุต

• C_j = คลาสที่เชื่อมโยงกับ j^th หน่วยเอาต์พุต

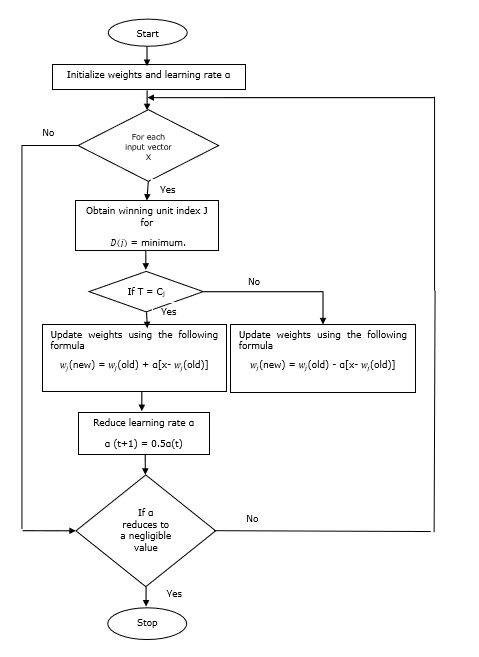
อัลกอริทึมการฝึกอบรม

Step 1 - เริ่มต้นเวกเตอร์อ้างอิงซึ่งสามารถทำได้ดังนี้ -

• Step 1(a) - จากชุดเวกเตอร์การฝึกที่กำหนดให้เลือก "m” (จำนวนคลัสเตอร์) ฝึกเวกเตอร์และใช้เป็นเวกเตอร์น้ำหนัก เวกเตอร์ที่เหลือสามารถใช้สำหรับการฝึกอบรม

• Step 1(b) - กำหนดน้ำหนักเริ่มต้นและการจำแนกแบบสุ่ม

• Step 1(c) - ใช้ K-mean clustering method

Step 2 - เริ่มต้นเวกเตอร์อ้างอิง $ \ alpha $

Step 3 - ทำตามขั้นตอนที่ 4-9 ต่อไปหากไม่เป็นไปตามเงื่อนไขในการหยุดอัลกอริทึมนี้

Step 4 - ทำตามขั้นตอนที่ 5-6 สำหรับเวกเตอร์อินพุตการฝึกทุกตัว x.

Step 5 - คำนวณกำลังสองของระยะทางแบบยุคลิดสำหรับ j = 1 to m และ i = 1 to n

$$ D (j) \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 6 - รับหน่วยที่ชนะ J ที่ไหน D(j) เป็นขั้นต่ำ

Step 7 - คำนวณน้ำหนักใหม่ของหน่วยที่ชนะตามความสัมพันธ์ต่อไปนี้ -

ถ้า T = C_j แล้ว $ w_ {j} (ใหม่) \: = \: w_ {j} (เก่า) \: + \: \ alpha [x \: - \: w_ {j} (เก่า)] $

ถ้า T ≠ C_j แล้ว $ w_ {j} (ใหม่) \: = \: w_ {j} (เก่า) \: - \: \ alpha [x \: - \: w_ {j} (เก่า)] $

Step 8 - ลดอัตราการเรียนรู้ $ \ alpha $

Step 9- ทดสอบสภาพการหยุด อาจเป็นดังนี้ -

• ถึงจำนวนสูงสุดของยุคแล้ว
• อัตราการเรียนรู้ลดลงเหลือเพียงเล็กน้อย

ผังงาน

ตัวแปร

อีกสามสายพันธุ์ ได้แก่ LVQ2, LVQ2.1 และ LVQ3 ได้รับการพัฒนาโดย Kohonen ความซับซ้อนในทั้งสามสายพันธุ์เนื่องจากแนวคิดที่ว่าผู้ชนะและหน่วยรองชนะเลิศจะได้เรียนรู้มากกว่าใน LVQ

LVQ2

ตามที่กล่าวไว้แนวคิดของสายพันธุ์อื่น ๆ ของ LVQ ข้างต้นเงื่อนไขของ LVQ2 ถูกสร้างขึ้นโดยหน้าต่าง หน้าต่างนี้จะขึ้นอยู่กับพารามิเตอร์ต่อไปนี้ -

• x - เวกเตอร์อินพุตปัจจุบัน

• y_c - เวกเตอร์อ้างอิงที่ใกล้เคียงที่สุด x

• y_r - เวกเตอร์อ้างอิงอื่น ๆ ซึ่งอยู่ใกล้ที่สุด x

• d_c - ระยะทางจาก x ถึง y_c

• d_r - ระยะทางจาก x ถึง y_r

เวกเตอร์อินพุต x ตกหน้าต่างถ้า

$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: และ \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$

ที่นี่ $ \ theta $ คือจำนวนตัวอย่างการฝึกอบรม

การอัปเดตสามารถทำได้ด้วยสูตรต่อไปนี้ -

$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (ท)] $ (belongs to different class)

$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (ท)] $ (belongs to same class)

ที่นี่ $ \ alpha $ คืออัตราการเรียนรู้

LVQ2.1

ใน LVQ2.1 เราจะหาเวกเตอร์ที่ใกล้เคียงที่สุดสองตัวคือ y_c1 และ y_c2 และเงื่อนไขสำหรับหน้าต่างมีดังนี้ -

$$ นาที \ เริ่มต้น {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$

$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$

การอัปเดตสามารถทำได้ด้วยสูตรต่อไปนี้ -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (ท)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (ท)] $ (belongs to same class)

ที่นี่ $ \ alpha $ คืออัตราการเรียนรู้

LVQ3

ใน LVQ3 เราจะหาเวกเตอร์ที่ใกล้เคียงที่สุดสองตัวคือ y_c1 และ y_c2 และเงื่อนไขสำหรับหน้าต่างมีดังนี้ -

$$ นาที \ เริ่มต้น {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$

ที่นี่ $ \ theta \ ประมาณ 0.2 $

การอัปเดตสามารถทำได้ด้วยสูตรต่อไปนี้ -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (ท)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (ท)] $ (belongs to same class)

ที่นี่ $ \ beta $ คือผลคูณของอัตราการเรียนรู้ $ \ alpha $ และ $\beta\:=\:m \alpha(t)$ สำหรับทุกๆ 0.1 < m < 0.5

เครือข่ายนี้ได้รับการพัฒนาโดย Stephen Grossberg และ Gail Carpenter ในปี 1987 โดยมีพื้นฐานมาจากการแข่งขันและใช้รูปแบบการเรียนรู้ที่ไม่มีผู้ดูแล เครือข่าย Adaptive Resonance Theory (ART) ตามชื่อที่แนะนำนั้นเปิดกว้างสำหรับการเรียนรู้ใหม่ ๆ (ปรับตัวได้) โดยไม่สูญเสียรูปแบบเก่า ๆ โดยทั่วไปเครือข่าย ART เป็นลักษณนามเวกเตอร์ซึ่งรับเวกเตอร์อินพุตและจำแนกเป็นประเภทใดประเภทหนึ่งขึ้นอยู่กับรูปแบบที่จัดเก็บไว้ซึ่งคล้ายคลึงกันมากที่สุด

หัวหน้าฝ่ายปฏิบัติการ

การดำเนินการหลักของการจำแนกประเภท ART สามารถแบ่งออกเป็นขั้นตอนต่อไปนี้ -

• Recognition phase- เวกเตอร์อินพุตถูกเปรียบเทียบกับการจำแนกประเภทที่นำเสนอในทุกโหนดในชั้นเอาต์พุต ผลลัพธ์ของเซลล์ประสาทจะกลายเป็น“ 1” หากตรงกับการจำแนกประเภทที่ใช้มากที่สุดมิฉะนั้นจะกลายเป็น“ 0”

• Comparison phase- ในขั้นตอนนี้จะทำการเปรียบเทียบเวกเตอร์อินพุตกับเวกเตอร์เลเยอร์เปรียบเทียบ เงื่อนไขสำหรับการรีเซ็ตคือระดับของความคล้ายคลึงกันจะน้อยกว่าพารามิเตอร์การเฝ้าระวัง

• Search phase- ในขั้นตอนนี้เครือข่ายจะค้นหาการรีเซ็ตและการจับคู่ที่ทำในขั้นตอนข้างต้น ดังนั้นหากไม่มีการรีเซ็ตและการแข่งขันค่อนข้างดีการจัดประเภทจะสิ้นสุดลง มิฉะนั้นกระบวนการจะซ้ำและต้องส่งรูปแบบอื่น ๆ ที่จัดเก็บไว้เพื่อค้นหาการจับคู่ที่ถูกต้อง

ART1

เป็น ART ประเภทหนึ่งซึ่งออกแบบมาเพื่อจัดกลุ่มเวกเตอร์ไบนารี เราสามารถเข้าใจเกี่ยวกับเรื่องนี้ได้ด้วยสถาปัตยกรรมของมัน

สถาปัตยกรรมของ ART1

ประกอบด้วยสองหน่วยต่อไปนี้ -

Computational Unit - ประกอบด้วยสิ่งต่อไปนี้ -

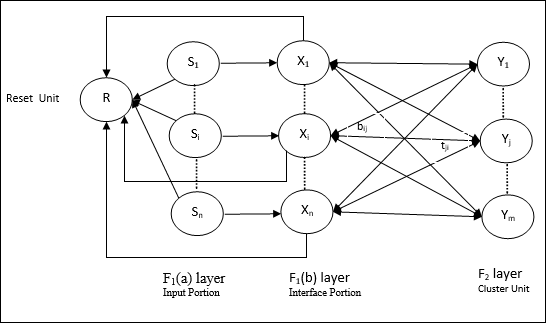
• Input unit (F₁ layer) - นอกจากนี้ยังมีสองส่วนต่อไปนี้ -

  • F₁(a) layer (Input portion)- ใน ART1 จะไม่มีการประมวลผลในส่วนนี้แทนที่จะมีเวกเตอร์อินพุตเท่านั้น เชื่อมต่อกับเลเยอร์F ₁ (b) (ส่วนอินเตอร์เฟส)

  • F₁(b) layer (Interface portion)- ส่วนนี้รวมสัญญาณจากส่วนอินพุตกับเลเยอร์F ₂ เลเยอร์F ₁ (b) เชื่อมต่อกับเลเยอร์F ₂โดยใช้น้ำหนักจากล่างขึ้นบนb_ijและชั้นF ₂เชื่อมต่อกับชั้น F ₁ (b) ผ่านน้ำหนักจากบนลงล่างt_ji.

• Cluster Unit (F₂ layer)- นี่คือเลเยอร์การแข่งขัน หน่วยที่มีอินพุตสุทธิที่ใหญ่ที่สุดถูกเลือกเพื่อเรียนรู้รูปแบบการป้อนข้อมูล การเปิดใช้งานของคลัสเตอร์ยูนิตอื่น ๆ ทั้งหมดถูกตั้งค่าเป็น 0

• Reset Mechanism- การทำงานของกลไกนี้ขึ้นอยู่กับความคล้ายคลึงกันระหว่างน้ำหนักจากบนลงล่างและเวกเตอร์อินพุต ตอนนี้ถ้าระดับของความคล้ายคลึงกันนี้น้อยกว่าพารามิเตอร์การเฝ้าระวังคลัสเตอร์จะไม่ได้รับอนุญาตให้เรียนรู้รูปแบบและส่วนที่เหลือจะเกิดขึ้น

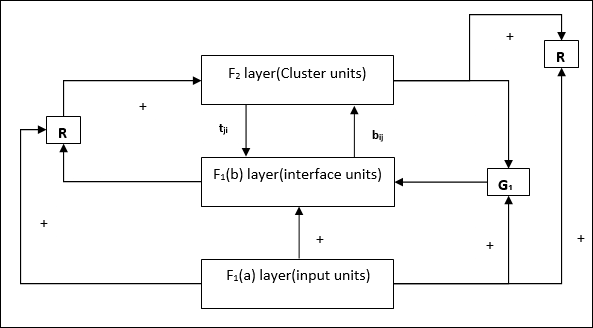
Supplement Unit - จริงๆแล้วปัญหาเกี่ยวกับกลไกการรีเซ็ตก็คือเลเยอร์ F₂จะต้องถูกยับยั้งภายใต้เงื่อนไขบางประการและจะต้องพร้อมใช้งานเมื่อเกิดการเรียนรู้บางอย่าง นั่นคือเหตุผลที่หน่วยเสริมสองหน่วย ได้แก่G₁ และ G₂ ถูกเพิ่มพร้อมกับหน่วยรีเซ็ต R. พวกเขาเรียกว่าgain control units. หน่วยเหล่านี้รับและส่งสัญญาณไปยังหน่วยอื่น ๆ ที่มีอยู่ในเครือข่าย‘+’ บ่งบอกถึงสัญญาณกระตุ้นในขณะที่ ‘−’ บ่งบอกถึงสัญญาณยับยั้ง

พารามิเตอร์ที่ใช้

ใช้พารามิเตอร์ต่อไปนี้ -

• n - จำนวนส่วนประกอบในเวกเตอร์อินพุต

• m - จำนวนคลัสเตอร์สูงสุดที่สามารถสร้างได้

• b_ij- น้ำหนักตั้งแต่ F ₁ (b) ถึง F ₂ชั้นคือน้ำหนักจากล่างขึ้นบน

• t_ji- น้ำหนักตั้งแต่ชั้น F ₂ถึง F ₁ (b) คือน้ำหนักจากบนลงล่าง

• ρ - พารามิเตอร์การเฝ้าระวัง

• ||x|| - บรรทัดฐานของเวกเตอร์ x

อัลกอริทึม

Step 1 - เริ่มต้นอัตราการเรียนรู้พารามิเตอร์การเฝ้าระวังและน้ำหนักดังนี้ -

$$ \ alpha \:> \: 1 \: \: และ \: \: 0 \: <\ rho \: \ leq \: 1 $$

$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: และ \: \: t_ {ij} (0) \: = \: 1 $$

Step 2 - ทำต่อขั้นตอนที่ 3-9 เมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ดำเนินการต่อในขั้นตอนที่ 4-6 สำหรับทุกการฝึกอบรม

Step 4- ตั้งค่าการเปิดใช้งานของหน่วย F ₁ (a) และ F ₁ทั้งหมดดังนี้

F₂ = 0 and F₁(a) = input vectors

Step 5- ต้องส่งสัญญาณอินพุตจากเลเยอร์F ₁ (a) ถึง F ₁ (b) เช่น

$$ s_ {i} \: = \: x_ {i} $$

Step 6- สำหรับทุกโหนดF _{2 ที่}ถูกยับยั้ง

$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ เงื่อนไขคือ y_j ≠ -1

Step 7 - ทำตามขั้นตอนที่ 8-10 เมื่อการรีเซ็ตเป็นจริง

Step 8 - ค้นหา J สำหรับ y_J ≥ y_j สำหรับโหนดทั้งหมด j

Step 9- คำนวณการเปิดใช้งานอีกครั้งใน F ₁ (b) ดังนี้

$$ x_ {i} \: = \: sitJi $$

Step 10 - ตอนนี้หลังจากคำนวณบรรทัดฐานของเวกเตอร์แล้ว x และเวกเตอร์ sเราต้องตรวจสอบเงื่อนไขการรีเซ็ตดังนี้ -

ถ้า ||x||/ ||s|| <พารามิเตอร์การเฝ้าระวัง ρ, ⁡then⁡inhibit⁡node J และไปที่ขั้นตอนที่ 7

อื่น ๆ ถ้า ||x||/ ||s|| ≥พารามิเตอร์การเฝ้าระวัง ρจากนั้นดำเนินการต่อไป

Step 11 - อัปเดตน้ำหนักสำหรับโหนด J สามารถทำได้ดังนี้ -

$$ b_ {ij} (ใหม่) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$

$$ t_ {ij} (ใหม่) \: = \: x_ {i} $$

Step 12 - ต้องตรวจสอบเงื่อนไขการหยุดสำหรับอัลกอริทึมและอาจเป็นดังนี้ -

• ห้ามมีการเปลี่ยนแปลงของน้ำหนัก
• ไม่ได้ทำการรีเซ็ตสำหรับหน่วย
• ถึงจำนวนสูงสุดของยุคแล้ว

สมมติว่าเรามีรูปแบบของมิติตามอำเภอใจอย่างไรก็ตามเราต้องการมิติเหล่านี้ในมิติเดียวหรือสองมิติ จากนั้นกระบวนการทำแผนที่คุณลักษณะจะมีประโยชน์มากในการแปลงพื้นที่รูปแบบกว้างให้เป็นพื้นที่คุณลักษณะทั่วไป ตอนนี้คำถามเกิดขึ้นว่าทำไมเราต้องมีแผนผังคุณลักษณะการจัดระเบียบตนเอง? เหตุผลก็คือพร้อมกับความสามารถในการแปลงขนาดตามอำเภอใจให้เป็น 1-D หรือ 2-D แล้วยังต้องมีความสามารถในการรักษาโทโพโลยีเพื่อนบ้าน

โครงสร้างเพื่อนบ้านใน Kohonen SOM

อาจมีโทโพโลยีหลายแบบอย่างไรก็ตามโทโพโลยีสองแบบต่อไปนี้ถูกใช้มากที่สุด -

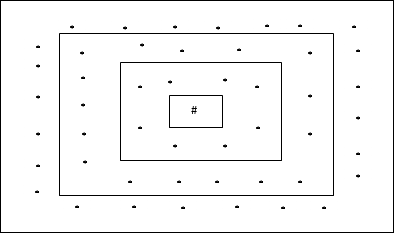
โครงสร้างตารางสี่เหลี่ยม

โทโพโลยีนี้มี 24 โหนดในกริดระยะทาง -2, 16 โหนดในตารางระยะทาง -1 และ 8 โหนดในตารางระยะทาง -0 ซึ่งหมายความว่าความแตกต่างระหว่างกริดสี่เหลี่ยมแต่ละโหนดคือ 8 โหนด หน่วยที่ชนะแสดงด้วย #

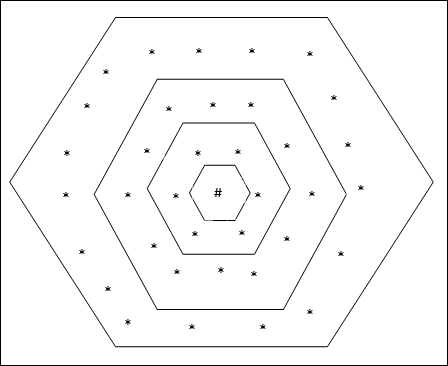
โครงสร้างตารางหกเหลี่ยม

โทโพโลยีนี้มี 18 โหนดในตารางระยะทาง -2, 12 โหนดในตารางระยะทาง -1 และ 6 โหนดในตารางระยะทาง -0 ซึ่งหมายความว่าความแตกต่างระหว่างกริดสี่เหลี่ยมแต่ละอันคือ 6 โหนด หน่วยที่ชนะแสดงด้วย #

สถาปัตยกรรม

สถาปัตยกรรมของ KSOM นั้นคล้ายกับเครือข่ายการแข่งขัน ด้วยความช่วยเหลือของโครงร่างพื้นที่ใกล้เคียงที่กล่าวถึงก่อนหน้านี้การฝึกอบรมสามารถเกิดขึ้นในพื้นที่ขยายของเครือข่าย

อัลกอริทึมสำหรับการฝึกอบรม

Step 1 - เริ่มต้นน้ำหนักอัตราการเรียนรู้ α และโครงการทอพอโลยีของพื้นที่ใกล้เคียง

Step 2 - ทำต่อขั้นตอนที่ 3-9 เมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ดำเนินการต่อในขั้นตอนที่ 4-6 สำหรับทุกอินพุตเวกเตอร์ x.

Step 4 - คำนวณกำลังสองของระยะทางแบบยุคลิดสำหรับ j = 1 to m

$$ D (j) \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 5 - รับหน่วยที่ชนะ J ที่ไหน D(j) เป็นขั้นต่ำ

Step 6 - คำนวณน้ำหนักใหม่ของหน่วยที่ชนะตามความสัมพันธ์ต่อไปนี้ -

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (เก่า)] $$

Step 7 - อัปเดตอัตราการเรียนรู้ α ตามความสัมพันธ์ต่อไปนี้ -

$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$

Step 8 - ลดรัศมีของโครงร่างโทโพโลยี

Step 9 - ตรวจสอบเงื่อนไขการหยุดสำหรับเครือข่าย

เครือข่ายประสาทเทียมประเภทนี้ทำงานบนพื้นฐานของการเชื่อมโยงรูปแบบซึ่งหมายความว่าพวกเขาสามารถจัดเก็บรูปแบบที่แตกต่างกันและในขณะที่ให้เอาต์พุตพวกเขาสามารถสร้างรูปแบบที่จัดเก็บอย่างใดอย่างหนึ่งโดยจับคู่กับรูปแบบการป้อนข้อมูลที่กำหนด ความทรงจำประเภทนี้เรียกอีกอย่างว่าContent-Addressable Memory(ลูกเบี้ยว). Associative memory ทำการค้นหาแบบขนานด้วยรูปแบบที่จัดเก็บไว้เป็นไฟล์ข้อมูล

ต่อไปนี้เป็นความทรงจำเชื่อมโยงสองประเภทที่เราสามารถสังเกตได้ -

• Auto Associative Memory
• หน่วยความจำ Hetero Associative

Auto Associative Memory

นี่คือโครงข่ายประสาทชั้นเดียวที่เวกเตอร์การฝึกอินพุตและเวกเตอร์เป้าหมายของเอาต์พุตเหมือนกัน น้ำหนักจะถูกกำหนดเพื่อให้เครือข่ายเก็บชุดรูปแบบ

สถาปัตยกรรม

ดังแสดงในรูปต่อไปนี้สถาปัตยกรรมของเครือข่ายหน่วยความจำ Auto Associative มี ‘n’ จำนวนเวกเตอร์การฝึกป้อนข้อมูลและสิ่งที่คล้ายกัน ‘n’ จำนวนเวกเตอร์เป้าหมายเอาต์พุต

อัลกอริทึมการฝึกอบรม

สำหรับการฝึกอบรมเครือข่ายนี้ใช้กฎการเรียนรู้ Hebb หรือ Delta

Step 1 - เริ่มต้นน้ำหนักทั้งหมดเป็นศูนย์เป็น w_ij = 0 (i = 1 to n, j = 1 to n)

Step 2 - ทำตามขั้นตอนที่ 3-4 สำหรับเวกเตอร์อินพุตแต่ละตัว

Step 3 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 4 - เปิดใช้งานเอาต์พุตแต่ละยูนิตดังนี้ -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: ถึง \: n) $$

Step 5 - ปรับน้ำหนักดังนี้ -

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: x_ {i} y_ {j} $$

อัลกอริทึมการทดสอบ

Step 1 - กำหนดน้ำหนักที่ได้รับระหว่างการฝึกตามกฎของเฮบบ์

Step 2 - ทำตามขั้นตอนที่ 3-5 สำหรับเวกเตอร์อินพุตแต่ละตัว

Step 3 - ตั้งค่าการเปิดใช้งานหน่วยอินพุตให้เท่ากับเวกเตอร์อินพุต

Step 4 - คำนวณอินพุตสุทธิของแต่ละหน่วยเอาต์พุต j = 1 to n

$$ y_ {อันตราย} \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อคำนวณผลลัพธ์

$$ y_ {j} \: = \: f (y_ {อันตราย}) \: = \: \ begin {cases} +1 & if \: y_ {อันตราย} \:> \: 0 \\ - 1 & if \: y_ {อันตราย} \: \ leqslant \: 0 \ end {cases} $$

หน่วยความจำ Hetero Associative

คล้ายกับเครือข่าย Auto Associative Memory ซึ่งเป็นเครือข่ายประสาทชั้นเดียว อย่างไรก็ตามในเครือข่ายนี้เวกเตอร์การฝึกอินพุตและเวกเตอร์เป้าหมายของเอาต์พุตจะไม่เหมือนกัน น้ำหนักจะถูกกำหนดเพื่อให้เครือข่ายเก็บชุดรูปแบบ เครือข่ายการเชื่อมโยง Hetero เป็นแบบคงที่ดังนั้นจึงไม่มีการดำเนินการที่ไม่ใช่เชิงเส้นและล่าช้า

สถาปัตยกรรม

ดังแสดงในรูปต่อไปนี้สถาปัตยกรรมของเครือข่าย Hetero Associative Memory มี ‘n’ จำนวนเวกเตอร์การฝึกป้อนข้อมูลและ ‘m’ จำนวนเวกเตอร์เป้าหมายเอาต์พุต

อัลกอริทึมการฝึกอบรม

สำหรับการฝึกอบรมเครือข่ายนี้ใช้กฎการเรียนรู้ Hebb หรือ Delta

Step 1 - เริ่มต้นน้ำหนักทั้งหมดเป็นศูนย์เป็น w_ij = 0 (i = 1 to n, j = 1 to m)

Step 2 - ทำตามขั้นตอนที่ 3-4 สำหรับเวกเตอร์อินพุตแต่ละตัว

Step 3 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$

Step 4 - เปิดใช้งานเอาต์พุตแต่ละยูนิตดังนี้ -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: ถึง \: m) $$

Step 5 - ปรับน้ำหนักดังนี้ -

$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: x_ {i} y_ {j} $$

อัลกอริทึมการทดสอบ

Step 1 - กำหนดน้ำหนักที่ได้รับระหว่างการฝึกตามกฎของเฮบบ์

Step 2 - ทำตามขั้นตอนที่ 3-5 สำหรับเวกเตอร์อินพุตแต่ละตัว

Step 3 - ตั้งค่าการเปิดใช้งานหน่วยอินพุตให้เท่ากับเวกเตอร์อินพุต

Step 4 - คำนวณอินพุตสุทธิของแต่ละหน่วยเอาต์พุต j = 1 to m;

$$ y_ {อันตราย} \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อคำนวณผลลัพธ์

$$ y_ {j} \: = \: f (y_ {อันตราย}) \: = \: \ begin {cases} +1 & if \: y_ {อันตราย} \:> \: 0 \\ 0 & if \ : y_ {อันตราย} \: = \: 0 \\ - 1 & if \: y_ {อันตราย} \: <\: 0 \ end {cases} $$

โครงข่ายประสาทเทียม Hopfield ถูกคิดค้นโดยดร. จอห์นเจ. ฮ็อปฟิลด์ในปี พ.ศ. 2525 ประกอบด้วยชั้นเดียวซึ่งประกอบด้วยเซลล์ประสาทที่เกิดซ้ำที่เชื่อมต่อกันอย่างสมบูรณ์อย่างน้อยหนึ่งเซลล์ เครือข่าย Hopfield มักใช้สำหรับการเชื่อมโยงอัตโนมัติและงานการเพิ่มประสิทธิภาพ

เครือข่าย Hopfield แบบไม่ต่อเนื่อง

เครือข่าย Hopfield ซึ่งทำงานในรูปแบบเส้นแยกหรือกล่าวอีกนัยหนึ่งอาจกล่าวได้ว่ารูปแบบอินพุตและเอาต์พุตเป็นเวกเตอร์ที่ไม่ต่อเนื่องซึ่งอาจเป็นได้ทั้งไบนารี (0,1) หรือไบโพลาร์ (+1, -1) ในธรรมชาติ เครือข่ายมีน้ำหนักสมมาตรโดยไม่มีการเชื่อมต่อด้วยตนเองเช่นw_ij = w_ji และ w_ii = 0.

สถาปัตยกรรม

ต่อไปนี้เป็นประเด็นสำคัญบางประการที่ควรทราบเกี่ยวกับเครือข่าย Hopfield แบบไม่ต่อเนื่อง -

• แบบจำลองนี้ประกอบด้วยเซลล์ประสาทที่มีการกลับด้านหนึ่งตัวและหนึ่งเอาต์พุตที่ไม่กลับด้าน

• ผลลัพธ์ของเซลล์ประสาทแต่ละเซลล์ควรเป็นข้อมูลของเซลล์ประสาทอื่น ๆ แต่ไม่ใช่ข้อมูลของตัวเอง

• น้ำหนัก / ความแข็งแรงของการเชื่อมต่อแสดงโดย w_ij.

• การเชื่อมต่อสามารถกระตุ้นได้เช่นเดียวกับการยับยั้ง มันจะถูกกระตุ้นถ้าผลลัพธ์ของเซลล์ประสาทเหมือนกับอินพุตมิฉะนั้นจะถูกยับยั้ง

• น้ำหนักควรสมมาตรกล่าวคือ w_ij = w_ji

ผลลัพธ์จาก Y₁ กำลังจะ Y₂, Y_i และ Y_n มีน้ำหนัก w₁₂, w_1i และ w_1nตามลำดับ ในทำนองเดียวกันส่วนโค้งอื่น ๆ ก็มีน้ำหนักอยู่

อัลกอริทึมการฝึกอบรม

ในระหว่างการฝึกอบรมเครือข่าย Hopfield แบบไม่ต่อเนื่องน้ำหนักจะถูกอัปเดต ดังที่เราทราบว่าเราสามารถมีเวกเตอร์อินพุตไบนารีเช่นเดียวกับเวกเตอร์อินพุตสองขั้ว ดังนั้นในทั้งสองกรณีการอัปเดตน้ำหนักสามารถทำได้ด้วยความสัมพันธ์ต่อไปนี้

Case 1 - รูปแบบการป้อนข้อมูลไบนารี

สำหรับชุดรูปแบบไบนารี s(p), p = 1 to P

ที่นี่ s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Weight Matrix กำหนดโดย

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: สำหรับ \: i \: \ neq \: j $$

Case 2 - รูปแบบการป้อนข้อมูลสองขั้ว

สำหรับชุดรูปแบบไบนารี s(p), p = 1 to P

ที่นี่ s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Weight Matrix กำหนดโดย

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: สำหรับ \ : i \: \ neq \: j $$

อัลกอริทึมการทดสอบ

Step 1 - เริ่มต้นน้ำหนักซึ่งได้รับจากอัลกอริทึมการฝึกอบรมโดยใช้หลักการ Hebbian

Step 2 - ทำตามขั้นตอนที่ 3-9 หากการเปิดใช้งานเครือข่ายไม่รวมเข้าด้วยกัน

Step 3 - สำหรับเวกเตอร์อินพุตแต่ละรายการ Xทำตามขั้นตอนที่ 4-8

Step 4 - ทำการเปิดใช้งานครั้งแรกของเครือข่ายเท่ากับเวกเตอร์อินพุตภายนอก X ดังต่อไปนี้ -

$$ y_ {i} \: = \: x_ {i} \: \: \: สำหรับ \: i \: = \: 1 \: ถึง \: n $$

Step 5 - สำหรับแต่ละยูนิต Y_iทำตามขั้นตอนที่ 6-9

Step 6 - คำนวณอินพุตสุทธิของเครือข่ายดังนี้ -

$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ LIMIT_ {j} y_ {j} w_ {ji} $$

Step 7 - ใช้การเปิดใช้งานดังต่อไปนี้เหนืออินพุตสุทธิเพื่อคำนวณผลลัพธ์ -

$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {cases} $$

นี่ $ \ theta_ {i} $ คือเกณฑ์

Step 8 - ออกอากาศเอาต์พุตนี้ y_i ไปยังหน่วยอื่น ๆ ทั้งหมด

Step 9 - ทดสอบเครือข่ายสำหรับการเชื่อมต่อ

การประเมินฟังก์ชันพลังงาน

ฟังก์ชันพลังงานถูกกำหนดให้เป็นฟังก์ชันที่ถูกผูกมัดและไม่เพิ่มฟังก์ชันของสถานะของระบบ

ฟังก์ชันพลังงาน E_f⁡, ⁡เรียกอีกอย่างว่า Lyapunov function กำหนดความเสถียรของเครือข่าย Hopfield แบบไม่ต่อเนื่องและมีลักษณะดังนี้ -

$$ E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ theta_ {i} y_ {i} $$

Condition - ในเครือข่ายที่เสถียรเมื่อใดก็ตามที่สถานะของโหนดเปลี่ยนไปฟังก์ชันพลังงานข้างต้นจะลดลง

สมมติว่าเมื่อโหนด i ได้เปลี่ยนสถานะจาก $ y_i ^ {(k)} $ เป็น $ y_i ^ {(k \: + \: 1)} $ ⁡จากนั้นการเปลี่ยนแปลงพลังงาน $ \ Delta E_ {f} $ จะได้รับจากความสัมพันธ์ต่อไปนี้

$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$

$$ = \: - \ left (\ start {array} {c} \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$

$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$

ที่นี่ $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $

การเปลี่ยนแปลงของพลังงานขึ้นอยู่กับข้อเท็จจริงที่ว่ามีเพียงหน่วยเดียวเท่านั้นที่สามารถอัปเดตการเปิดใช้งานได้ในแต่ละครั้ง

เครือข่าย Hopfield อย่างต่อเนื่อง

เมื่อเปรียบเทียบกับเครือข่าย Discrete Hopfield เครือข่ายแบบต่อเนื่องมีเวลาเป็นตัวแปรต่อเนื่อง นอกจากนี้ยังใช้ในการเชื่อมโยงอัตโนมัติและปัญหาการเพิ่มประสิทธิภาพเช่นปัญหาพนักงานขายในการเดินทาง

Model - โมเดลหรือสถาปัตยกรรมสามารถสร้างขึ้นได้โดยการเพิ่มส่วนประกอบไฟฟ้าเช่นแอมพลิฟายเออร์ซึ่งสามารถแมปแรงดันไฟฟ้าขาเข้ากับแรงดันไฟฟ้าขาออกผ่านฟังก์ชันการกระตุ้นซิกมอยด์

การประเมินฟังก์ชันพลังงาน

$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$

ที่นี่ λ คือพารามิเตอร์กำไรและ g_ri การนำไฟฟ้าเข้า

สิ่งเหล่านี้เป็นกระบวนการเรียนรู้แบบสุ่มที่มีโครงสร้างเกิดขึ้นซ้ำและเป็นพื้นฐานของเทคนิคการเพิ่มประสิทธิภาพขั้นต้นที่ใช้ใน ANN Boltzmann Machine ถูกคิดค้นโดย Geoffrey Hinton และ Terry Sejnowski ในปี 1985 ความชัดเจนมากขึ้นสามารถสังเกตได้จากคำพูดของ Hinton เกี่ยวกับ Boltzmann Machine

“ คุณสมบัติที่น่าแปลกใจของเครือข่ายนี้คือใช้เฉพาะข้อมูลที่มีอยู่ในท้องถิ่นเท่านั้น การเปลี่ยนแปลงของน้ำหนักขึ้นอยู่กับพฤติกรรมของทั้งสองหน่วยที่เชื่อมต่อกันแม้ว่าการเปลี่ยนแปลงจะเพิ่มประสิทธิภาพการวัดระดับโลกก็ตาม” - Ackley, Hinton 1985

ประเด็นสำคัญบางประการเกี่ยวกับเครื่อง Boltzmann -

• พวกเขาใช้โครงสร้างที่เกิดซ้ำ

• ประกอบด้วยเซลล์ประสาทสุ่มซึ่งมีหนึ่งในสองสถานะที่เป็นไปได้คือ 1 หรือ 0

• เซลล์ประสาทบางส่วนในนี้ปรับตัวได้ (สถานะอิสระ) และบางส่วนถูกยึด (สถานะแช่แข็ง)

• หากเราใช้การอบแบบจำลองบนเครือข่าย Hopfield แบบแยกส่วนมันก็จะกลายเป็น Boltzmann Machine

วัตถุประสงค์ของเครื่อง Boltzmann

วัตถุประสงค์หลักของ Boltzmann Machine คือการเพิ่มประสิทธิภาพการแก้ปัญหา เป็นผลงานของ Boltzmann Machine ในการปรับน้ำหนักและปริมาณที่เกี่ยวข้องกับปัญหานั้นให้เหมาะสม

สถาปัตยกรรม

แผนภาพต่อไปนี้แสดงสถาปัตยกรรมของเครื่อง Boltzmann เห็นได้ชัดจากแผนภาพว่าเป็นอาร์เรย์สองมิติของหน่วย ที่นี่น้ำหนักเกี่ยวกับการเชื่อมต่อระหว่างหน่วยคือ–p ที่ไหน p > 0. น้ำหนักของการเชื่อมต่อด้วยตนเองได้รับจากb ที่ไหน b > 0.

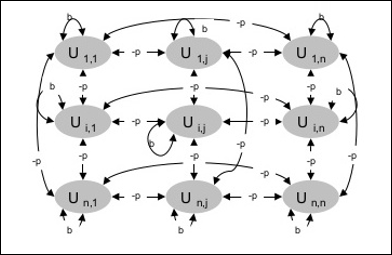
อัลกอริทึมการฝึกอบรม

อย่างที่เราทราบกันดีว่าเครื่อง Boltzmann มีน้ำหนักคงที่ดังนั้นจึงไม่มีอัลกอริทึมการฝึกอบรมเนื่องจากเราไม่จำเป็นต้องอัปเดตน้ำหนักในเครือข่าย อย่างไรก็ตามในการทดสอบเครือข่ายเราต้องตั้งค่าน้ำหนักและค้นหาฟังก์ชันฉันทามติ (CF)

เครื่อง Boltzmann มีชุดหน่วย U_i และ U_j และมีการเชื่อมต่อแบบสองทิศทาง

• เรากำลังพิจารณาน้ำหนักคงที่พูด w_ij.

• w_ij ≠ 0 ถ้า U_i และ U_j มีการเชื่อมต่อ

• นอกจากนี้ยังมีความสมมาตรในการเชื่อมต่อโครงข่ายแบบถ่วงน้ำหนักเช่น w_ij = w_ji.

• w_ii นอกจากนี้ยังมีอยู่เช่นจะมีการเชื่อมต่อระหว่างหน่วย

• สำหรับยูนิตใด ๆ U_iสถานะของมัน u_i จะเป็น 1 หรือ 0

วัตถุประสงค์หลักของ Boltzmann Machine คือการเพิ่ม Consensus Function (CF) ให้มากที่สุดซึ่งสามารถกำหนดได้จากความสัมพันธ์ต่อไปนี้

$$ CF \: = \: \ displaystyle \ sum \ LIMIT_ {i} \ displaystyle \ sum \ LIMIT_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

ตอนนี้เมื่อสถานะเปลี่ยนจาก 1 เป็น 0 หรือจาก 0 เป็น 1 การเปลี่ยนแปลงฉันทามติสามารถกำหนดได้โดยความสัมพันธ์ต่อไปนี้ -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ LIMIT_ {j \ neq i} u_ {i} w_ { ij}) $$

ที่นี่ u_i คือสถานะปัจจุบันของ U_i.

ความแปรผันของค่าสัมประสิทธิ์ (1 - 2u_i) กำหนดโดยความสัมพันธ์ต่อไปนี้ -

$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {cases} +1, & U_ {i} \: is \: current \: off \\ - 1, & U_ {i } \: is \: ปัจจุบัน \: เมื่อ \ end {cases} $$

โดยทั่วไปหน่วย U_iไม่เปลี่ยนสถานะ แต่ถ้าเป็นเช่นนั้นข้อมูลจะอยู่ในพื้นที่ของหน่วย ด้วยการเปลี่ยนแปลงดังกล่าวก็จะมีฉันทามติของเครือข่ายเพิ่มขึ้นด้วย

ความน่าจะเป็นของเครือข่ายที่จะยอมรับการเปลี่ยนแปลงในสถานะของหน่วยจะได้รับจากความสัมพันธ์ต่อไปนี้ -

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

ที่นี่ Tเป็นพารามิเตอร์ควบคุม มันจะลดลงเมื่อ CF ถึงค่าสูงสุด

อัลกอริทึมการทดสอบ

Step 1 - เริ่มต้นสิ่งต่อไปนี้เพื่อเริ่มการฝึกอบรม -

• น้ำหนักที่แสดงถึงข้อ จำกัด ของปัญหา
• พารามิเตอร์ควบคุม T

Step 2 - ทำตามขั้นตอนที่ 3-8 ต่อเมื่อเงื่อนไขการหยุดไม่เป็นจริง

Step 3 - ทำตามขั้นตอนที่ 4-7

Step 4 - สมมติว่าสถานะใดสถานะหนึ่งได้เปลี่ยนน้ำหนักและเลือกจำนวนเต็ม I, J เป็นค่าสุ่มระหว่าง 1 และ n.

Step 5 - คำนวณการเปลี่ยนแปลงของฉันทามติดังนี้ -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ LIMIT_ {j \ neq i} u_ {i} w_ { ij}) $$

Step 6 - คำนวณความน่าจะเป็นที่เครือข่ายนี้จะยอมรับการเปลี่ยนแปลงสถานะ

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Step 7 - ยอมรับหรือปฏิเสธการเปลี่ยนแปลงนี้ดังนี้ -

Case I - ถ้า R < AFยอมรับการเปลี่ยนแปลง

Case II - ถ้า R ≥ AFปฏิเสธการเปลี่ยนแปลง

ที่นี่ R คือตัวเลขสุ่มระหว่าง 0 ถึง 1

Step 8 - ลดพารามิเตอร์ควบคุม (อุณหภูมิ) ดังนี้ -

T(new) = ⁡0.95T(old)

Step 9 - ทดสอบเงื่อนไขการหยุดซึ่งอาจเป็นดังนี้ -

• อุณหภูมิถึงค่าที่กำหนด
• ไม่มีการเปลี่ยนแปลงสถานะสำหรับการทำซ้ำตามจำนวนที่ระบุ

Brain-State-in-a-Box (BSB) neural network เป็นเครือข่ายประสาทเทียมแบบ nonlinear auto-Associative และสามารถขยายไปสู่การเชื่อมโยงแบบ hetero ที่มีสองเลเยอร์ขึ้นไป นอกจากนี้ยังคล้ายกับเครือข่าย Hopfield เสนอโดย JA Anderson, JW Silverstein, SA Ritz และ RS Jones ในปีพ. ศ. 2520

ประเด็นสำคัญที่ต้องจำเกี่ยวกับ BSB Network -

• เป็นเครือข่ายที่เชื่อมต่อเต็มรูปแบบโดยมีจำนวนโหนดสูงสุดขึ้นอยู่กับขนาด n ของพื้นที่ป้อนข้อมูล

• เซลล์ประสาททั้งหมดได้รับการอัปเดตพร้อมกัน

• เซลล์ประสาทรับค่าระหว่าง -1 ถึง +1

สูตรทางคณิตศาสตร์

ฟังก์ชันโหนดที่ใช้ในเครือข่าย BSB เป็นฟังก์ชันทางลาดซึ่งสามารถกำหนดได้ดังนี้ -

$$ f (net) \: = \: min (1, \: max (-1, \: net)) $$

ฟังก์ชันทางลาดนี้มีขอบเขตและต่อเนื่อง

ดังที่เราทราบว่าแต่ละโหนดจะเปลี่ยนสถานะสามารถทำได้ด้วยความช่วยเหลือของความสัมพันธ์ทางคณิตศาสตร์ต่อไปนี้ -

$$ x_ {t} (t \: + \: 1) \: = \: f \ left (\ begin {array} {c} \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n w_ {i, j } x_ {j} (t) \ end {array} \ right) $$

ที่นี่ x_i(t) คือสถานะของไฟล์ i_th โหนดในเวลา t.

น้ำหนักจาก i_th โหนดถึง j_th โหนดสามารถวัดได้ด้วยความสัมพันธ์ต่อไปนี้ -

$$ w_ {ij} \: = \: \ frac {1} {P} \ displaystyle \ sum \ LIMIT_ {p = 1} ^ P (v_ {p, i} \: v_ {p, j}) $$

ที่นี่ P คือจำนวนรูปแบบการฝึกอบรมซึ่งเป็นสองขั้ว

การเพิ่มประสิทธิภาพเป็นการดำเนินการเพื่อให้บางสิ่งบางอย่างเช่นการออกแบบสถานการณ์ทรัพยากรและระบบมีประสิทธิภาพมากที่สุด การใช้ความคล้ายคลึงกันระหว่างฟังก์ชันต้นทุนและฟังก์ชันพลังงานเราสามารถใช้เซลล์ประสาทที่เชื่อมต่อกันอย่างมากเพื่อแก้ปัญหาการเพิ่มประสิทธิภาพ เครือข่ายประสาทชนิดดังกล่าวคือเครือข่าย Hopfield ซึ่งประกอบด้วยชั้นเดียวที่มีเซลล์ประสาทที่เกิดซ้ำที่เชื่อมต่อกันอย่างสมบูรณ์อย่างน้อยหนึ่งเซลล์ สามารถใช้เพื่อเพิ่มประสิทธิภาพ

สิ่งที่ต้องจำขณะใช้เครือข่าย Hopfield เพื่อการเพิ่มประสิทธิภาพ -

• ฟังก์ชันพลังงานต้องต่ำสุดของเครือข่าย

• จะพบวิธีแก้ปัญหาที่น่าพอใจแทนที่จะเลือกรูปแบบที่จัดเก็บไว้

• คุณภาพของโซลูชันที่พบโดยเครือข่าย Hopfield นั้นขึ้นอยู่กับสถานะเริ่มต้นของเครือข่ายอย่างมีนัยสำคัญ

ปัญหาพนักงานขายในการเดินทาง

การค้นหาเส้นทางที่สั้นที่สุดที่พนักงานขายเดินทางเป็นหนึ่งในปัญหาด้านการคำนวณซึ่งสามารถปรับให้เหมาะสมได้โดยใช้เครือข่ายประสาทเทียม Hopfield

แนวคิดพื้นฐานของ TSP

Travelling Salesman Problem (TSP) เป็นปัญหาการเพิ่มประสิทธิภาพแบบคลาสสิกที่พนักงานขายต้องเดินทาง nเมืองที่เชื่อมต่อกันโดยรักษาค่าใช้จ่ายตลอดจนระยะทางที่เดินทางต่ำสุด ตัวอย่างเช่นพนักงานขายต้องเดินทาง 4 เมือง A, B, C, D และเป้าหมายคือค้นหาทัวร์วงกลมที่สั้นที่สุด ABC – D เพื่อลดค่าใช้จ่ายให้น้อยที่สุดซึ่งรวมถึงค่าใช้จ่ายในการเดินทางจาก เมืองสุดท้าย D ไปยังเมืองแรก A

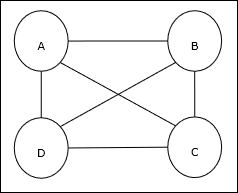
การเป็นตัวแทนเมทริกซ์

จริงๆแล้ว TSP แต่ละครั้งของ n-city สามารถแสดงเป็นไฟล์ n × n เมทริกซ์ที่มี i_th แถวอธิบายไฟล์ i_thที่ตั้งของเมือง. เมทริกซ์นี้Mสำหรับ 4 เมือง A, B, C, D สามารถแสดงได้ดังนี้ -

$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$

โซลูชันโดย Hopfield Network

ในขณะที่พิจารณาโซลูชันของ TSP โดยเครือข่าย Hopfield นี้ทุกโหนดในเครือข่ายจะสอดคล้องกับองค์ประกอบหนึ่งในเมทริกซ์

การคำนวณฟังก์ชันพลังงาน

เพื่อให้เป็นโซลูชันที่เหมาะสมที่สุดฟังก์ชันพลังงานจะต้องมีค่าต่ำสุด บนพื้นฐานของข้อ จำกัด ต่อไปนี้เราสามารถคำนวณฟังก์ชันพลังงานได้ดังนี้ -

ข้อ จำกัด - I

ข้อ จำกัด ประการแรกบนพื้นฐานที่เราจะคำนวณฟังก์ชันพลังงานคือองค์ประกอบหนึ่งจะต้องเท่ากับ 1 ในแต่ละแถวของเมทริกซ์ M และองค์ประกอบอื่น ๆ ในแต่ละแถวต้องเท่ากับ 0เนื่องจากแต่ละเมืองสามารถเกิดขึ้นได้เพียงตำแหน่งเดียวใน TSP tour ข้อ จำกัด นี้สามารถเขียนทางคณิตศาสตร์ได้ดังนี้ -

$$ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: สำหรับ \: x \: \ in \: \ lbrace1, ... , n \ rbrace $ $

ตอนนี้ฟังก์ชันพลังงานที่จะย่อเล็กสุดตามข้อ จำกัด ข้างต้นจะมีคำที่เป็นสัดส่วนกับ -

$$ \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

ข้อ จำกัด -II

ดังที่เราทราบใน TSP หนึ่งเมืองสามารถเกิดขึ้นได้ในตำแหน่งใดก็ได้ในทัวร์ด้วยเหตุนี้ในแต่ละคอลัมน์ของเมทริกซ์ Mองค์ประกอบหนึ่งต้องเท่ากับ 1 และองค์ประกอบอื่น ๆ ต้องเท่ากับ 0 ข้อ จำกัด นี้สามารถเขียนทางคณิตศาสตร์ได้ดังนี้ -

$$ \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: สำหรับ \: j \: \ in \: \ lbrace1, ... , n \ rbrace $ $

ตอนนี้ฟังก์ชันพลังงานที่จะย่อเล็กสุดตามข้อ จำกัด ข้างต้นจะมีคำที่เป็นสัดส่วนกับ -

$$ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

การคำนวณฟังก์ชันต้นทุน

สมมติว่าเมทริกซ์กำลังสองของ (n × n) แสดงโดย C หมายถึงเมทริกซ์ต้นทุนของ TSP สำหรับ n เมืองที่ n > 0. ต่อไปนี้เป็นพารามิเตอร์บางส่วนในขณะคำนวณฟังก์ชันต้นทุน -

• C_{x, y} - องค์ประกอบของเมทริกซ์ต้นทุนแสดงถึงต้นทุนการเดินทางจากเมือง x ถึง y.

• ความคลาดเคลื่อนขององค์ประกอบของ A และ B สามารถแสดงได้ด้วยความสัมพันธ์ต่อไปนี้ -

$$ M_ {x, i} \: = \: 1 \: \: and \: \: M_ {y, i \ pm 1} \: = \: 1 $$

ดังที่เราทราบใน Matrix ค่าเอาต์พุตของแต่ละโหนดอาจเป็น 0 หรือ 1 ดังนั้นสำหรับทุกคู่ของเมือง A, B เราสามารถเพิ่มเงื่อนไขต่อไปนี้ในฟังก์ชันพลังงาน -

$$ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$

บนพื้นฐานของฟังก์ชันต้นทุนและค่าข้อ จำกัด ข้างต้นฟังก์ชันพลังงานขั้นสุดท้าย E ได้ดังนี้ -

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {x} \ displaystyle \ sum \ LIMIT_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$

$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ LIMIT_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ LIMIT_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ LIMIT_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$

ที่นี่ γ₁ และ γ₂ คือค่าคงที่ในการชั่งน้ำหนักสองค่า

เทคนิคการไล่ระดับสีแบบวนซ้ำ

การไล่ระดับสีหรือที่เรียกว่าโคตรชันที่สุดคืออัลกอริธึมการเพิ่มประสิทธิภาพแบบวนซ้ำเพื่อค้นหาฟังก์ชันขั้นต่ำในพื้นที่ ในขณะที่ลดฟังก์ชันลงเรามีความกังวลกับค่าใช้จ่ายหรือข้อผิดพลาดที่จะลดลง (จดจำปัญหาพนักงานขายในการเดินทาง) มีการใช้อย่างกว้างขวางในการเรียนรู้เชิงลึกซึ่งมีประโยชน์ในหลากหลายสถานการณ์ ประเด็นที่ต้องจำไว้คือเราเกี่ยวข้องกับการเพิ่มประสิทธิภาพในพื้นที่ไม่ใช่การเพิ่มประสิทธิภาพระดับโลก

แนวคิดการทำงานหลัก

เราสามารถเข้าใจแนวคิดการทำงานหลักของการไล่ระดับสีด้วยความช่วยเหลือของขั้นตอนต่อไปนี้ -

• ขั้นแรกเริ่มต้นด้วยการเดาทางแก้ปัญหาเบื้องต้น

• จากนั้นใช้การไล่ระดับสีของฟังก์ชันที่จุดนั้น

• จากนั้นให้ทำซ้ำขั้นตอนโดยก้าวโซลูชันไปในทิศทางลบของการไล่ระดับสี

โดยทำตามขั้นตอนข้างต้นในที่สุดอัลกอริทึมจะมาบรรจบกันโดยที่การไล่ระดับสีเป็นศูนย์

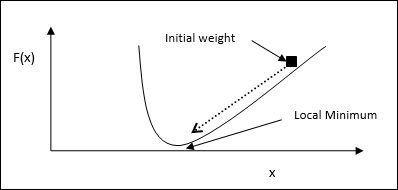
แนวคิดทางคณิตศาสตร์

สมมติว่าเรามีฟังก์ชัน f(x)และเรากำลังพยายามหาค่าต่ำสุดของฟังก์ชันนี้ ต่อไปนี้เป็นขั้นตอนในการค้นหาขั้นต่ำของf(x).

• ขั้นแรกให้ค่าเริ่มต้น $ x_ {0} \: สำหรับ \: x $

• ตอนนี้ใช้การไล่ระดับสี $ \ nabla f $ ⁡ของฟังก์ชันโดยสัญชาตญาณว่าการไล่ระดับสีจะให้ความชันของเส้นโค้งที่ x และทิศทางจะชี้ไปที่การเพิ่มขึ้นของฟังก์ชันเพื่อหาทิศทางที่ดีที่สุดในการย่อขนาด

• ตอนนี้เปลี่ยน x ดังนี้ -

  $$ x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n}) $$

ที่นี่ θ > 0 คืออัตราการฝึก (ขนาดขั้นตอน) ที่บังคับให้อัลกอริทึมต้องกระโดดเล็กน้อย

การประมาณขนาดขั้นตอน

ขนาดขั้นตอนที่ไม่ถูกต้องจริงๆ θอาจไปไม่ถึงการบรรจบกันดังนั้นการเลือกอย่างรอบคอบจึงมีความสำคัญมาก ต้องจำประเด็นต่อไปนี้ในขณะที่เลือกขนาดขั้นตอน

• อย่าเลือกขนาดของขั้นตอนที่ใหญ่เกินไปมิฉะนั้นจะมีผลกระทบในทางลบกล่าวคือมันจะแตกต่างกันมากกว่าที่จะมาบรรจบกัน

• อย่าเลือกขนาดขั้นตอนที่เล็กเกินไปมิฉะนั้นจะใช้เวลามากในการบรรจบกัน

ตัวเลือกบางอย่างเกี่ยวกับการเลือกขนาดขั้นตอน -

• ทางเลือกหนึ่งคือเลือกขนาดขั้นตอนคงที่

• อีกทางเลือกหนึ่งคือการเลือกขนาดขั้นตอนอื่นสำหรับการทำซ้ำทุกครั้ง

การหลอมจำลอง

แนวคิดพื้นฐานของ Simulated Annealing (SA) ได้รับแรงบันดาลใจจากการหลอมในของแข็ง ในกระบวนการหลอมโลหะหากเราให้ความร้อนโลหะเหนือจุดหลอมเหลวและทำให้โลหะเย็นลงคุณสมบัติของโครงสร้างจะขึ้นอยู่กับอัตราการหล่อเย็น เรายังสามารถพูดได้ว่า SA จำลองกระบวนการหลอมโลหะ

ใช้ใน ANN

SA เป็นวิธีการคำนวณแบบสุ่มซึ่งได้รับแรงบันดาลใจจากการเปรียบเทียบการหลอมเพื่อประมาณการเพิ่มประสิทธิภาพทั่วโลกของฟังก์ชันที่กำหนด เราสามารถใช้ SA เพื่อฝึกเครือข่ายประสาทฟีดไปข้างหน้า

อัลกอริทึม

Step 1 - สร้างโซลูชันแบบสุ่ม

Step 2 - คำนวณต้นทุนโดยใช้ฟังก์ชันต้นทุน

Step 3 - สร้างโซลูชันใกล้เคียงแบบสุ่ม

Step 4 - คำนวณต้นทุนโซลูชันใหม่โดยใช้ฟังก์ชันต้นทุนเดียวกัน

Step 5 - เปรียบเทียบต้นทุนของโซลูชันใหม่กับโซลูชันเก่าดังนี้ -

ถ้า Cost_{New Solution} < Cost_{Old Solution} จากนั้นย้ายไปที่โซลูชันใหม่

Step 6 - ทดสอบเงื่อนไขการหยุดซึ่งอาจเป็นจำนวนครั้งสูงสุดของการทำซ้ำที่ถึงหรือได้รับโซลูชันที่ยอมรับได้

ธรรมชาติเป็นแหล่งที่มาของแรงบันดาลใจที่ดีสำหรับมวลมนุษยชาติ Genetic Algorithms (GAs) เป็นอัลกอริธึมที่ใช้การค้นหาตามแนวคิดของการคัดเลือกโดยธรรมชาติและพันธุศาสตร์ GAs เป็นชุดย่อยของสาขาการคำนวณที่ใหญ่กว่าที่เรียกว่าEvolutionary Computation.

GAs ได้รับการพัฒนาโดย John Holland และนักศึกษาและเพื่อนร่วมงานของเขาที่ University of Michigan โดยเฉพาะอย่างยิ่ง David E.Goldberg และได้รับการทดลองในปัญหาการเพิ่มประสิทธิภาพต่างๆพร้อมกับความสำเร็จในระดับสูง

ใน GAs เรามีกลุ่มหรือกลุ่มของวิธีแก้ปัญหาที่เป็นไปได้สำหรับปัญหาที่กำหนด จากนั้นวิธีการแก้ปัญหาเหล่านี้จะผ่านการรวมตัวกันใหม่และการกลายพันธุ์ (เช่นเดียวกับในพันธุศาสตร์ตามธรรมชาติ) ผลิตลูกใหม่และกระบวนการนี้ซ้ำแล้วซ้ำอีกในชั่วอายุต่างๆ แต่ละคน (หรือวิธีการแก้ปัญหาของผู้สมัคร) จะได้รับการกำหนดค่าสมรรถภาพ (ตามค่าฟังก์ชันวัตถุประสงค์) และบุคคลที่มีความเหมาะสมจะได้รับโอกาสที่สูงกว่าในการผสมพันธุ์และให้ผลตอบแทนแก่บุคคลที่ "ช่างฟิต" มากขึ้น ซึ่งสอดคล้องกับทฤษฎีดาร์วินเรื่อง“ Survival of the Fittest”

ด้วยวิธีนี้เราจะ“ พัฒนา” บุคคลหรือแนวทางแก้ไขที่ดีขึ้นเรื่อย ๆ มาหลายชั่วอายุคนจนกว่าจะถึงเกณฑ์ที่หยุดชะงัก

อัลกอริทึมทางพันธุกรรมมีการสุ่มอย่างเพียงพอในลักษณะ แต่จะทำงานได้ดีกว่าการค้นหาในพื้นที่แบบสุ่มมาก (ซึ่งเราลองใช้วิธีการสุ่มแบบต่างๆเพื่อติดตามสิ่งที่ดีที่สุดจนถึงตอนนี้) เนื่องจากใช้ประโยชน์จากข้อมูลในอดีตเช่นกัน

ข้อดีของ GAs

GAs มีข้อดีหลายประการซึ่งทำให้พวกเขาได้รับความนิยมอย่างกว้างขวาง ซึ่ง ได้แก่ -

• ไม่ต้องการข้อมูลอนุพันธ์ใด ๆ (ซึ่งอาจไม่มีให้สำหรับปัญหาในโลกแห่งความเป็นจริง)

• เร็วขึ้นและมีประสิทธิภาพมากขึ้นเมื่อเทียบกับวิธีการแบบเดิม

• มีความสามารถแบบขนานที่ดีมาก

• ปรับฟังก์ชั่นทั้งแบบต่อเนื่องและไม่ต่อเนื่องตลอดจนปัญหาหลายวัตถุประสงค์

• แสดงรายการโซลูชันที่ "ดี" ไม่ใช่แค่โซลูชันเดียว

• มักจะได้รับคำตอบสำหรับปัญหาซึ่งจะดีขึ้นเมื่อเวลาผ่านไป

• มีประโยชน์เมื่อพื้นที่ค้นหามีขนาดใหญ่มากและมีพารามิเตอร์จำนวนมากที่เกี่ยวข้อง

ข้อ จำกัด ของ GAs

เช่นเดียวกับเทคนิคอื่น ๆ GAs ก็มีข้อ จำกัด บางประการเช่นกัน ซึ่ง ได้แก่ -

• GAs ไม่เหมาะกับทุกปัญหาโดยเฉพาะปัญหาที่เรียบง่ายและมีข้อมูลอนุพันธ์

• ค่าฟิตเนสจะคำนวณซ้ำ ๆ ซึ่งอาจมีราคาแพงในการคำนวณสำหรับปัญหาบางอย่าง

• การสุ่มตัวอย่างจะไม่มีการรับประกันเกี่ยวกับความเหมาะสมหรือคุณภาพของโซลูชัน

• หากไม่ได้ติดตั้งอย่างถูกต้อง GA อาจไม่รวมเข้ากับโซลูชันที่เหมาะสมที่สุด

GA - แรงจูงใจ

อัลกอริทึมทางพันธุกรรมมีความสามารถในการนำเสนอโซลูชันที่ "ดีเพียงพอ" "เร็วพอ" สิ่งนี้ทำให้ Gas น่าสนใจสำหรับใช้ในการแก้ปัญหาการเพิ่มประสิทธิภาพ เหตุผลที่ GAs จำเป็นมีดังต่อไปนี้ -

การแก้ปัญหาที่ยาก

ในวิทยาการคอมพิวเตอร์มีปัญหาชุดใหญ่ซึ่ง ได้แก่ NP-Hard. สิ่งนี้หมายความว่าโดยพื้นฐานแล้วแม้แต่ระบบคอมพิวเตอร์ที่ทรงพลังที่สุดก็ใช้เวลานานมาก (เป็นปี!) ในการแก้ปัญหานั้น ในสถานการณ์เช่นนี้ GAs พิสูจน์แล้วว่าเป็นเครื่องมือที่มีประสิทธิภาพในการจัดหาusable near-optimal solutions ในช่วงเวลาสั้น ๆ

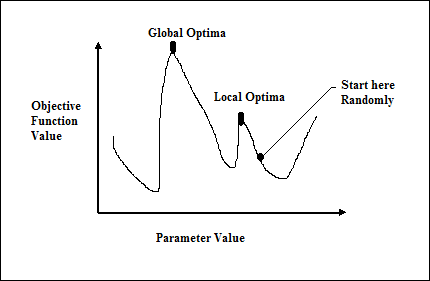
ความล้มเหลวของวิธีการไล่ระดับสี

วิธีการที่ใช้แคลคูลัสแบบดั้งเดิมทำงานโดยเริ่มจากจุดสุ่มและโดยการเคลื่อนที่ไปตามทิศทางของการไล่ระดับสีจนกระทั่งเราไปถึงจุดสูงสุดของเนินเขา เทคนิคนี้มีประสิทธิภาพและใช้ได้ผลดีกับฟังก์ชันวัตถุประสงค์จุดยอดเดียวเช่นฟังก์ชันต้นทุนในการถดถอยเชิงเส้น อย่างไรก็ตามในสถานการณ์จริงส่วนใหญ่เรามีปัญหาที่ซับซ้อนมากที่เรียกว่าภูมิประเทศซึ่งประกอบด้วยยอดเขาจำนวนมากและหุบเขาจำนวนมากซึ่งทำให้วิธีการดังกล่าวล้มเหลวเนื่องจากพวกเขาต้องทนทุกข์ทรมานจากแนวโน้มที่จะติดอยู่ที่ Optima ในท้องถิ่นดังที่แสดง ในรูปต่อไปนี้

รับทางออกที่ดีอย่างรวดเร็ว

ปัญหาที่ยากบางอย่างเช่นปัญหาพนักงานขายการเดินทาง (TSP) มีแอปพลิเคชันในโลกแห่งความเป็นจริงเช่นการค้นหาเส้นทางและการออกแบบ VLSI ลองนึกภาพว่าคุณกำลังใช้ระบบการนำทางด้วย GPS และใช้เวลาสองสามนาที (หรือสองสามชั่วโมง) ในการคำนวณเส้นทางที่ "เหมาะสมที่สุด" จากต้นทางไปยังปลายทาง ความล่าช้าในแอปพลิเคชันในโลกแห่งความเป็นจริงนั้นไม่สามารถยอมรับได้ดังนั้นโซลูชันที่ "ดีเพียงพอ" ซึ่งส่งมอบให้ "เร็ว" จึงเป็นสิ่งที่จำเป็น

วิธีใช้ GA สำหรับปัญหาการเพิ่มประสิทธิภาพ

เราทราบดีอยู่แล้วว่าการเพิ่มประสิทธิภาพเป็นการกระทำเพื่อให้บางสิ่งบางอย่างเช่นการออกแบบสถานการณ์ทรัพยากรและระบบมีประสิทธิภาพมากที่สุด กระบวนการเพิ่มประสิทธิภาพจะแสดงในแผนภาพต่อไปนี้

ขั้นตอนของกลไก GA สำหรับกระบวนการเพิ่มประสิทธิภาพ

ต่อไปนี้เป็นขั้นตอนของกลไก GA เมื่อใช้เพื่อเพิ่มประสิทธิภาพของปัญหา

• สร้างประชากรเริ่มต้นแบบสุ่ม

• เลือกโซลูชันเริ่มต้นที่มีค่าสมรรถภาพที่ดีที่สุด

• รวมโซลูชันที่เลือกใหม่โดยใช้ตัวดำเนินการการกลายพันธุ์และครอสโอเวอร์

• แทรกลูกหลานเข้าไปในประชากร

• ตอนนี้หากตรงตามเงื่อนไขการหยุดแล้วให้ส่งคืนโซลูชันที่มีค่าสมรรถภาพที่ดีที่สุด จากนั้นไปที่ขั้นตอนที่ 2

ก่อนที่จะศึกษาสาขาที่ ANN ถูกนำไปใช้อย่างกว้างขวางเราจำเป็นต้องเข้าใจว่าเหตุใด ANN จึงเป็นตัวเลือกที่ต้องการของแอปพลิเคชัน

ทำไมต้องใช้โครงข่ายประสาทเทียม

เราจำเป็นต้องเข้าใจคำตอบของคำถามข้างต้นด้วยตัวอย่างของมนุษย์ ตอนเป็นเด็กเราเคยเรียนรู้สิ่งต่างๆโดยได้รับความช่วยเหลือจากผู้ปกครองซึ่งรวมถึงพ่อแม่หรือครูของเราด้วย หลังจากนั้นด้วยการเรียนรู้ด้วยตนเองหรือฝึกฝนทำให้เราเรียนรู้ไปตลอดชีวิต นักวิทยาศาสตร์และนักวิจัยยังทำให้เครื่องจักรมีความชาญฉลาดเช่นเดียวกับมนุษย์และ ANN ก็มีบทบาทสำคัญเช่นเดียวกันเนื่องจากเหตุผลดังต่อไปนี้ -

• ด้วยความช่วยเหลือของโครงข่ายประสาทเทียมเราสามารถค้นหาวิธีแก้ปัญหาดังกล่าวซึ่งวิธีการอัลกอริทึมมีราคาแพงหรือไม่มีอยู่จริง

• โครงข่ายประสาทเทียมสามารถเรียนรู้ได้ด้วยเหตุนี้เราจึงไม่จำเป็นต้องตั้งโปรแกรมในขอบเขตมากนัก

• โครงข่ายประสาทมีความแม่นยำและความเร็วที่รวดเร็วกว่าความเร็วทั่วไปอย่างมาก

พื้นที่การใช้งาน

ต่อไปนี้เป็นพื้นที่บางส่วนที่มีการใช้ ANN แสดงให้เห็นว่า ANN มีแนวทางสหวิทยาการในการพัฒนาและการประยุกต์ใช้

การรู้จำเสียง

คำพูดมีบทบาทสำคัญในปฏิสัมพันธ์ระหว่างมนุษย์กับมนุษย์ ดังนั้นจึงเป็นเรื่องธรรมดาที่ผู้คนจะคาดหวังการเชื่อมต่อด้วยเสียงกับคอมพิวเตอร์ ในยุคปัจจุบันสำหรับการสื่อสารกับเครื่องจักรมนุษย์ยังคงต้องการภาษาที่ซับซ้อนซึ่งยากต่อการเรียนรู้และใช้งาน เพื่อลดอุปสรรคในการสื่อสารนี้วิธีแก้ปัญหาง่ายๆคือการสื่อสารด้วยภาษาพูดที่เป็นไปได้เพื่อให้เครื่องเข้าใจ

มีความก้าวหน้าอย่างมากในสาขานี้อย่างไรก็ตามระบบประเภทนี้ยังคงประสบปัญหาเกี่ยวกับคำศัพท์หรือไวยากรณ์ที่ จำกัด พร้อมกับปัญหาในการฝึกอบรมระบบใหม่สำหรับผู้พูดที่แตกต่างกันในเงื่อนไขที่แตกต่างกัน ANN มีบทบาทสำคัญในด้านนี้ ANN ต่อไปนี้ถูกใช้เพื่อการรู้จำเสียง -

• เครือข่ายหลายชั้น

• เครือข่ายหลายชั้นที่มีการเชื่อมต่อซ้ำ

• แผนผังคุณลักษณะการจัดระเบียบตัวเองของ Kohonen

เครือข่ายที่มีประโยชน์ที่สุดสำหรับสิ่งนี้คือแผนผังคุณลักษณะการจัดระเบียบตัวเองของ Kohonen ซึ่งมีข้อมูลเข้าเป็นส่วนสั้น ๆ ของรูปคลื่นเสียงพูด จะแมปฟอนิมชนิดเดียวกันกับอาร์เรย์เอาต์พุตเรียกว่าเทคนิคการแยกคุณลักษณะ หลังจากแยกคุณสมบัติแล้วด้วยความช่วยเหลือของโมเดลอะคูสติกบางรุ่นเป็นการประมวลผลแบบแบ็คเอนด์มันจะจดจำเสียงพูด

การจดจำตัวละคร

เป็นปัญหาที่น่าสนใจซึ่งอยู่ภายใต้พื้นที่ทั่วไปของการจดจำรูปแบบ โครงข่ายประสาทเทียมจำนวนมากได้รับการพัฒนาเพื่อการจดจำอักขระที่เขียนด้วยลายมือโดยอัตโนมัติไม่ว่าจะเป็นตัวอักษรหรือตัวเลข ต่อไปนี้เป็น ANN บางส่วนที่ใช้ในการจดจำอักขระ -

• โครงข่ายประสาทเทียมหลายชั้นเช่นโครงข่ายประสาทแบบ Backpropagation
• Neocognitron

แม้ว่าเครือข่ายประสาทเทียมแบบย้อนกลับจะมีเลเยอร์ที่ซ่อนอยู่หลายชั้น แต่รูปแบบของการเชื่อมต่อจากชั้นหนึ่งไปยังชั้นถัดไปจะถูกแปลเป็นภาษาท้องถิ่น ในทำนองเดียวกัน neocognitron ยังมีเลเยอร์ที่ซ่อนอยู่หลายชั้นและการฝึกอบรมจะทำทีละชั้นสำหรับการใช้งานประเภทนี้

ใบสมัครยืนยันลายเซ็น

ลายเซ็นเป็นวิธีที่มีประโยชน์ที่สุดวิธีหนึ่งในการอนุญาตและรับรองความถูกต้องของบุคคลในธุรกรรมทางกฎหมาย เทคนิคการตรวจสอบลายเซ็นเป็นเทคนิคที่ไม่ใช้การมองเห็น

สำหรับแอปพลิเคชันนี้แนวทางแรกคือการแยกคุณลักษณะหรือชุดคุณลักษณะทางเรขาคณิตที่เป็นตัวแทนของลายเซ็น ด้วยชุดคุณลักษณะเหล่านี้เราต้องฝึกเครือข่ายประสาทโดยใช้อัลกอริทึมเครือข่ายประสาทเทียมที่มีประสิทธิภาพ โครงข่ายประสาทเทียมที่ผ่านการฝึกอบรมนี้จะจำแนกลายเซ็นว่าเป็นของแท้หรือปลอมแปลงภายใต้ขั้นตอนการตรวจสอบ

การจดจำใบหน้ามนุษย์

เป็นหนึ่งในวิธีการทางชีวภาพในการระบุใบหน้าที่กำหนด เป็นงานทั่วไปเนื่องจากการกำหนดลักษณะของภาพที่ "ไม่ใช่ใบหน้า" อย่างไรก็ตามหากโครงข่ายประสาทเทียมได้รับการฝึกฝนมาเป็นอย่างดีก็สามารถแบ่งออกเป็นสองประเภท ได้แก่ รูปภาพที่มีใบหน้าและรูปภาพที่ไม่มีใบหน้า

ขั้นแรกภาพที่ป้อนทั้งหมดจะต้องได้รับการประมวลผลล่วงหน้า จากนั้นความมีมิติของภาพนั้นจะต้องลดลง และในที่สุดก็ต้องจำแนกโดยใช้อัลกอริธึมการฝึกอบรมเครือข่ายประสาทเทียม โครงข่ายประสาทเทียมต่อไปนี้ใช้เพื่อวัตถุประสงค์ในการฝึกอบรมด้วยภาพที่ประมวลผลล่วงหน้า -

• โครงข่ายประสาทเทียมหลายชั้นที่เชื่อมต่ออย่างเต็มที่ได้รับการฝึกฝนด้วยความช่วยเหลือของอัลกอริธึมการแพร่กระจายกลับ

• สำหรับการลดขนาดจะใช้การวิเคราะห์องค์ประกอบหลัก (PCA)