การเพิ่มประสิทธิภาพโดยใช้ Hopfield Network
การเพิ่มประสิทธิภาพเป็นการดำเนินการเพื่อให้บางสิ่งบางอย่างเช่นการออกแบบสถานการณ์ทรัพยากรและระบบมีประสิทธิภาพมากที่สุด การใช้ความคล้ายคลึงกันระหว่างฟังก์ชันต้นทุนและฟังก์ชันพลังงานเราสามารถใช้เซลล์ประสาทที่เชื่อมต่อกันอย่างมากเพื่อแก้ปัญหาการเพิ่มประสิทธิภาพ เครือข่ายประสาทชนิดดังกล่าวคือเครือข่าย Hopfield ซึ่งประกอบด้วยชั้นเดียวที่มีเซลล์ประสาทที่เกิดซ้ำที่เชื่อมต่อกันอย่างสมบูรณ์อย่างน้อยหนึ่งเซลล์ สามารถใช้เพื่อเพิ่มประสิทธิภาพ
สิ่งที่ต้องจำขณะใช้เครือข่าย Hopfield เพื่อการเพิ่มประสิทธิภาพ -
ฟังก์ชันพลังงานต้องต่ำสุดของเครือข่าย
จะพบวิธีแก้ปัญหาที่น่าพอใจแทนที่จะเลือกรูปแบบที่จัดเก็บไว้
คุณภาพของโซลูชันที่พบโดยเครือข่าย Hopfield นั้นขึ้นอยู่กับสถานะเริ่มต้นของเครือข่ายอย่างมีนัยสำคัญ
ปัญหาพนักงานขายในการเดินทาง
การค้นหาเส้นทางที่สั้นที่สุดที่พนักงานขายเดินทางเป็นหนึ่งในปัญหาด้านการคำนวณซึ่งสามารถปรับให้เหมาะสมได้โดยใช้เครือข่ายประสาทเทียม Hopfield
แนวคิดพื้นฐานของ TSP
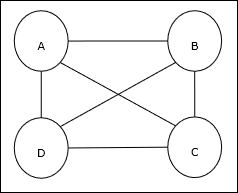
Travelling Salesman Problem (TSP) เป็นปัญหาการเพิ่มประสิทธิภาพแบบคลาสสิกที่พนักงานขายต้องเดินทาง nเมืองที่เชื่อมต่อกันโดยรักษาค่าใช้จ่ายตลอดจนระยะทางที่เดินทางต่ำสุด ตัวอย่างเช่นพนักงานขายต้องเดินทาง 4 เมือง A, B, C, D และเป้าหมายคือค้นหาทัวร์วงกลมที่สั้นที่สุด ABC – D เพื่อลดค่าใช้จ่ายให้น้อยที่สุดซึ่งรวมถึงค่าใช้จ่ายในการเดินทางจาก เมืองสุดท้าย D ไปยังเมืองแรก A
การเป็นตัวแทนเมทริกซ์
จริงๆแล้ว TSP แต่ละครั้งของ n-city สามารถแสดงเป็นไฟล์ n × n เมทริกซ์ที่มี ith แถวอธิบายไฟล์ ithที่ตั้งของเมือง. เมทริกซ์นี้Mสำหรับ 4 เมือง A, B, C, D สามารถแสดงได้ดังนี้ -
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
โซลูชันโดย Hopfield Network
ในขณะที่พิจารณาโซลูชันของ TSP โดยเครือข่าย Hopfield นี้ทุกโหนดในเครือข่ายจะสอดคล้องกับองค์ประกอบหนึ่งในเมทริกซ์
การคำนวณฟังก์ชันพลังงาน
เพื่อให้เป็นโซลูชันที่เหมาะสมที่สุดฟังก์ชันพลังงานจะต้องมีค่าต่ำสุด บนพื้นฐานของข้อ จำกัด ต่อไปนี้เราสามารถคำนวณฟังก์ชันพลังงานได้ดังนี้ -
ข้อ จำกัด - I
ข้อ จำกัด ประการแรกบนพื้นฐานที่เราจะคำนวณฟังก์ชันพลังงานคือองค์ประกอบหนึ่งจะต้องเท่ากับ 1 ในแต่ละแถวของเมทริกซ์ M และองค์ประกอบอื่น ๆ ในแต่ละแถวต้องเท่ากับ 0เนื่องจากแต่ละเมืองสามารถเกิดขึ้นได้เพียงตำแหน่งเดียวใน TSP tour ข้อ จำกัด นี้สามารถเขียนทางคณิตศาสตร์ได้ดังนี้ -
$$ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: สำหรับ \: x \: \ in \: \ lbrace1, ... , n \ rbrace $ $
ตอนนี้ฟังก์ชันพลังงานที่จะย่อเล็กสุดตามข้อ จำกัด ข้างต้นจะมีคำที่เป็นสัดส่วนกับ -
$$ \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
ข้อ จำกัด -II
ดังที่เราทราบใน TSP หนึ่งเมืองสามารถเกิดขึ้นได้ในตำแหน่งใดก็ได้ในทัวร์ด้วยเหตุนี้ในแต่ละคอลัมน์ของเมทริกซ์ Mองค์ประกอบหนึ่งต้องเท่ากับ 1 และองค์ประกอบอื่น ๆ ต้องเท่ากับ 0 ข้อ จำกัด นี้สามารถเขียนทางคณิตศาสตร์ได้ดังนี้ -
$$ \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: สำหรับ \: j \: \ in \: \ lbrace1, ... , n \ rbrace $ $
ตอนนี้ฟังก์ชันพลังงานที่จะย่อเล็กสุดตามข้อ จำกัด ข้างต้นจะมีคำที่เป็นสัดส่วนกับ -
$$ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
การคำนวณฟังก์ชันต้นทุน
สมมติว่าเมทริกซ์กำลังสองของ (n × n) แสดงโดย C หมายถึงเมทริกซ์ต้นทุนของ TSP สำหรับ n เมืองที่ n > 0. ต่อไปนี้เป็นพารามิเตอร์บางส่วนในขณะคำนวณฟังก์ชันต้นทุน -
Cx, y - องค์ประกอบของเมทริกซ์ต้นทุนแสดงถึงต้นทุนการเดินทางจากเมือง x ถึง y.
ความคลาดเคลื่อนขององค์ประกอบของ A และ B สามารถแสดงได้ด้วยความสัมพันธ์ต่อไปนี้ -
$$ M_ {x, i} \: = \: 1 \: \: and \: \: M_ {y, i \ pm 1} \: = \: 1 $$
ดังที่เราทราบใน Matrix ค่าเอาต์พุตของแต่ละโหนดอาจเป็น 0 หรือ 1 ดังนั้นสำหรับทุกคู่ของเมือง A, B เราสามารถเพิ่มเงื่อนไขต่อไปนี้ในฟังก์ชันพลังงาน -
$$ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
บนพื้นฐานของฟังก์ชันต้นทุนและค่าข้อ จำกัด ข้างต้นฟังก์ชันพลังงานขั้นสุดท้าย E ได้ดังนี้ -
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {x} \ displaystyle \ sum \ LIMIT_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ LIMIT_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ LIMIT_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ LIMIT_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ LIMIT_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
ที่นี่ γ1 และ γ2 คือค่าคงที่ในการชั่งน้ำหนักสองค่า