โครงข่ายประสาทเทียม - Hopfield Networks
โครงข่ายประสาทเทียม Hopfield ถูกคิดค้นโดยดร. จอห์นเจ. ฮ็อปฟิลด์ในปี พ.ศ. 2525 ประกอบด้วยชั้นเดียวซึ่งประกอบด้วยเซลล์ประสาทที่เกิดซ้ำที่เชื่อมต่อกันอย่างสมบูรณ์อย่างน้อยหนึ่งเซลล์ เครือข่าย Hopfield มักใช้สำหรับการเชื่อมโยงอัตโนมัติและงานการเพิ่มประสิทธิภาพ
เครือข่าย Hopfield แบบไม่ต่อเนื่อง
เครือข่าย Hopfield ซึ่งทำงานในรูปแบบเส้นแยกหรือกล่าวอีกนัยหนึ่งอาจกล่าวได้ว่ารูปแบบอินพุตและเอาต์พุตเป็นเวกเตอร์ที่ไม่ต่อเนื่องซึ่งอาจเป็นได้ทั้งไบนารี (0,1) หรือไบโพลาร์ (+1, -1) ในธรรมชาติ เครือข่ายมีน้ำหนักสมมาตรโดยไม่มีการเชื่อมต่อด้วยตนเองเช่นwij = wji และ wii = 0.
สถาปัตยกรรม
ต่อไปนี้เป็นประเด็นสำคัญบางประการที่ควรทราบเกี่ยวกับเครือข่าย Hopfield แบบไม่ต่อเนื่อง -
แบบจำลองนี้ประกอบด้วยเซลล์ประสาทที่มีการกลับด้านหนึ่งตัวและหนึ่งเอาต์พุตที่ไม่กลับด้าน
ผลลัพธ์ของเซลล์ประสาทแต่ละเซลล์ควรเป็นข้อมูลของเซลล์ประสาทอื่น ๆ แต่ไม่ใช่ข้อมูลของตัวเอง
น้ำหนัก / ความแข็งแรงของการเชื่อมต่อแสดงโดย wij.
การเชื่อมต่อสามารถกระตุ้นได้เช่นเดียวกับการยับยั้ง มันจะถูกกระตุ้นถ้าผลลัพธ์ของเซลล์ประสาทเหมือนกับอินพุตมิฉะนั้นจะถูกยับยั้ง
น้ำหนักควรสมมาตรกล่าวคือ wij = wji
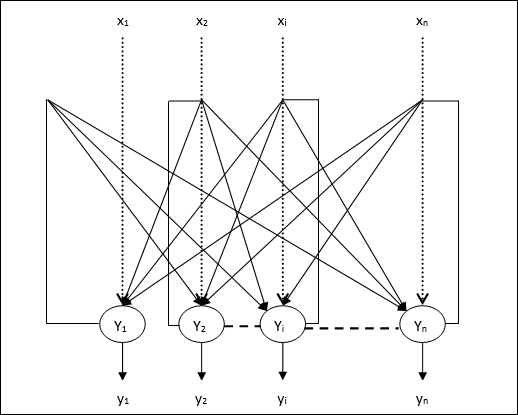
ผลลัพธ์จาก Y1 กำลังจะ Y2, Yi และ Yn มีน้ำหนัก w12, w1i และ w1nตามลำดับ ในทำนองเดียวกันส่วนโค้งอื่น ๆ ก็มีน้ำหนักอยู่
อัลกอริทึมการฝึกอบรม
ในระหว่างการฝึกอบรมเครือข่าย Hopfield แบบไม่ต่อเนื่องน้ำหนักจะถูกอัปเดต ดังที่เราทราบว่าเราสามารถมีเวกเตอร์อินพุตไบนารีเช่นเดียวกับเวกเตอร์อินพุตสองขั้ว ดังนั้นในทั้งสองกรณีการอัปเดตน้ำหนักสามารถทำได้ด้วยความสัมพันธ์ต่อไปนี้
Case 1 - รูปแบบการป้อนข้อมูลไบนารี
สำหรับชุดรูปแบบไบนารี s(p), p = 1 to P
ที่นี่ s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Weight Matrix กำหนดโดย
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: สำหรับ \: i \: \ neq \: j $$
Case 2 - รูปแบบการป้อนข้อมูลสองขั้ว
สำหรับชุดรูปแบบไบนารี s(p), p = 1 to P
ที่นี่ s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Weight Matrix กำหนดโดย
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: สำหรับ \ : i \: \ neq \: j $$
อัลกอริทึมการทดสอบ
Step 1 - เริ่มต้นน้ำหนักซึ่งได้รับจากอัลกอริทึมการฝึกอบรมโดยใช้หลักการ Hebbian
Step 2 - ทำตามขั้นตอนที่ 3-9 หากการเปิดใช้งานเครือข่ายไม่รวมเข้าด้วยกัน
Step 3 - สำหรับเวกเตอร์อินพุตแต่ละรายการ Xทำตามขั้นตอนที่ 4-8
Step 4 - ทำการเปิดใช้งานครั้งแรกของเครือข่ายเท่ากับเวกเตอร์อินพุตภายนอก X ดังต่อไปนี้ -
$$ y_ {i} \: = \: x_ {i} \: \: \: สำหรับ \: i \: = \: 1 \: ถึง \: n $$
Step 5 - สำหรับแต่ละยูนิต Yiทำตามขั้นตอนที่ 6-9
Step 6 - คำนวณอินพุตสุทธิของเครือข่ายดังนี้ -
$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ LIMIT_ {j} y_ {j} w_ {ji} $$
Step 7 - ใช้การเปิดใช้งานดังต่อไปนี้เหนืออินพุตสุทธิเพื่อคำนวณผลลัพธ์ -
$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {cases} $$
นี่ $ \ theta_ {i} $ คือเกณฑ์
Step 8 - ออกอากาศเอาต์พุตนี้ yi ไปยังหน่วยอื่น ๆ ทั้งหมด
Step 9 - ทดสอบเครือข่ายสำหรับการเชื่อมต่อ
การประเมินฟังก์ชันพลังงาน
ฟังก์ชันพลังงานถูกกำหนดให้เป็นฟังก์ชันที่ถูกผูกมัดและไม่เพิ่มฟังก์ชันของสถานะของระบบ
ฟังก์ชันพลังงาน Ef, เรียกอีกอย่างว่า Lyapunov function กำหนดความเสถียรของเครือข่าย Hopfield แบบไม่ต่อเนื่องและมีลักษณะดังนี้ -
$$ E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ theta_ {i} y_ {i} $$
Condition - ในเครือข่ายที่เสถียรเมื่อใดก็ตามที่สถานะของโหนดเปลี่ยนไปฟังก์ชันพลังงานข้างต้นจะลดลง
สมมติว่าเมื่อโหนด i ได้เปลี่ยนสถานะจาก $ y_i ^ {(k)} $ เป็น $ y_i ^ {(k \: + \: 1)} $ จากนั้นการเปลี่ยนแปลงพลังงาน $ \ Delta E_ {f} $ จะได้รับจากความสัมพันธ์ต่อไปนี้
$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$
$$ = \: - \ left (\ start {array} {c} \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$
$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$
ที่นี่ $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $
การเปลี่ยนแปลงของพลังงานขึ้นอยู่กับข้อเท็จจริงที่ว่ามีเพียงหน่วยเดียวเท่านั้นที่สามารถอัปเดตการเปิดใช้งานได้ในแต่ละครั้ง
เครือข่าย Hopfield อย่างต่อเนื่อง
เมื่อเปรียบเทียบกับเครือข่าย Discrete Hopfield เครือข่ายแบบต่อเนื่องมีเวลาเป็นตัวแปรต่อเนื่อง นอกจากนี้ยังใช้ในการเชื่อมโยงอัตโนมัติและปัญหาการเพิ่มประสิทธิภาพเช่นปัญหาพนักงานขายในการเดินทาง
Model - โมเดลหรือสถาปัตยกรรมสามารถสร้างขึ้นได้โดยการเพิ่มส่วนประกอบไฟฟ้าเช่นแอมพลิฟายเออร์ซึ่งสามารถแมปแรงดันไฟฟ้าขาเข้ากับแรงดันไฟฟ้าขาออกผ่านฟังก์ชันการกระตุ้นซิกมอยด์
การประเมินฟังก์ชันพลังงาน
$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$
ที่นี่ λ คือพารามิเตอร์กำไรและ gri การนำไฟฟ้าเข้า