เชื่อมโยงเครือข่ายหน่วยความจำ
เครือข่ายประสาทเทียมประเภทนี้ทำงานบนพื้นฐานของการเชื่อมโยงรูปแบบซึ่งหมายความว่าพวกเขาสามารถจัดเก็บรูปแบบที่แตกต่างกันและในขณะที่ให้เอาต์พุตพวกเขาสามารถสร้างรูปแบบที่จัดเก็บอย่างใดอย่างหนึ่งโดยจับคู่กับรูปแบบการป้อนข้อมูลที่กำหนด ความทรงจำประเภทนี้เรียกอีกอย่างว่าContent-Addressable Memory(ลูกเบี้ยว). Associative memory ทำการค้นหาแบบขนานด้วยรูปแบบที่จัดเก็บไว้เป็นไฟล์ข้อมูล
ต่อไปนี้เป็นความทรงจำเชื่อมโยงสองประเภทที่เราสามารถสังเกตได้ -
- Auto Associative Memory
- หน่วยความจำ Hetero Associative
Auto Associative Memory
นี่คือโครงข่ายประสาทชั้นเดียวที่เวกเตอร์การฝึกอินพุตและเวกเตอร์เป้าหมายของเอาต์พุตเหมือนกัน น้ำหนักจะถูกกำหนดเพื่อให้เครือข่ายเก็บชุดรูปแบบ
สถาปัตยกรรม
ดังแสดงในรูปต่อไปนี้สถาปัตยกรรมของเครือข่ายหน่วยความจำ Auto Associative มี ‘n’ จำนวนเวกเตอร์การฝึกป้อนข้อมูลและสิ่งที่คล้ายกัน ‘n’ จำนวนเวกเตอร์เป้าหมายเอาต์พุต
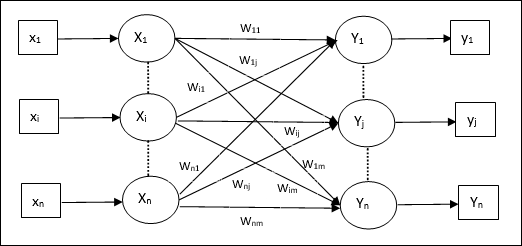
อัลกอริทึมการฝึกอบรม
สำหรับการฝึกอบรมเครือข่ายนี้ใช้กฎการเรียนรู้ Hebb หรือ Delta
Step 1 - เริ่มต้นน้ำหนักทั้งหมดเป็นศูนย์เป็น wij = 0 (i = 1 to n, j = 1 to n)
Step 2 - ทำตามขั้นตอนที่ 3-4 สำหรับเวกเตอร์อินพุตแต่ละตัว
Step 3 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -
$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$
Step 4 - เปิดใช้งานเอาต์พุตแต่ละยูนิตดังนี้ -
$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: ถึง \: n) $$
Step 5 - ปรับน้ำหนักดังนี้ -
$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: x_ {i} y_ {j} $$
อัลกอริทึมการทดสอบ
Step 1 - กำหนดน้ำหนักที่ได้รับระหว่างการฝึกตามกฎของเฮบบ์
Step 2 - ทำตามขั้นตอนที่ 3-5 สำหรับเวกเตอร์อินพุตแต่ละตัว
Step 3 - ตั้งค่าการเปิดใช้งานหน่วยอินพุตให้เท่ากับเวกเตอร์อินพุต
Step 4 - คำนวณอินพุตสุทธิของแต่ละหน่วยเอาต์พุต j = 1 to n
$$ y_ {อันตราย} \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อคำนวณผลลัพธ์
$$ y_ {j} \: = \: f (y_ {อันตราย}) \: = \: \ begin {cases} +1 & if \: y_ {อันตราย} \:> \: 0 \\ - 1 & if \: y_ {อันตราย} \: \ leqslant \: 0 \ end {cases} $$
หน่วยความจำ Hetero Associative
คล้ายกับเครือข่าย Auto Associative Memory ซึ่งเป็นเครือข่ายประสาทชั้นเดียว อย่างไรก็ตามในเครือข่ายนี้เวกเตอร์การฝึกอินพุตและเวกเตอร์เป้าหมายของเอาต์พุตจะไม่เหมือนกัน น้ำหนักจะถูกกำหนดเพื่อให้เครือข่ายเก็บชุดรูปแบบ เครือข่ายการเชื่อมโยง Hetero เป็นแบบคงที่ดังนั้นจึงไม่มีการดำเนินการที่ไม่ใช่เชิงเส้นและล่าช้า
สถาปัตยกรรม
ดังแสดงในรูปต่อไปนี้สถาปัตยกรรมของเครือข่าย Hetero Associative Memory มี ‘n’ จำนวนเวกเตอร์การฝึกป้อนข้อมูลและ ‘m’ จำนวนเวกเตอร์เป้าหมายเอาต์พุต
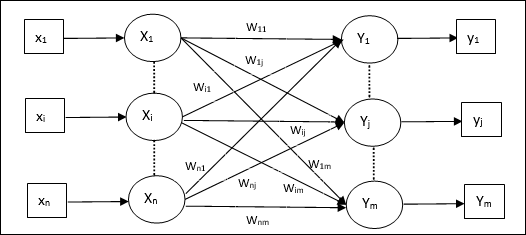
อัลกอริทึมการฝึกอบรม
สำหรับการฝึกอบรมเครือข่ายนี้ใช้กฎการเรียนรู้ Hebb หรือ Delta
Step 1 - เริ่มต้นน้ำหนักทั้งหมดเป็นศูนย์เป็น wij = 0 (i = 1 to n, j = 1 to m)
Step 2 - ทำตามขั้นตอนที่ 3-4 สำหรับเวกเตอร์อินพุตแต่ละตัว
Step 3 - เปิดใช้งานหน่วยอินพุตแต่ละหน่วยดังนี้ -
$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: ถึง \: n) $$
Step 4 - เปิดใช้งานเอาต์พุตแต่ละยูนิตดังนี้ -
$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: ถึง \: m) $$
Step 5 - ปรับน้ำหนักดังนี้ -
$$ w_ {ij} (ใหม่) \: = \: w_ {ij} (เก่า) \: + \: x_ {i} y_ {j} $$
อัลกอริทึมการทดสอบ
Step 1 - กำหนดน้ำหนักที่ได้รับระหว่างการฝึกตามกฎของเฮบบ์
Step 2 - ทำตามขั้นตอนที่ 3-5 สำหรับเวกเตอร์อินพุตแต่ละตัว
Step 3 - ตั้งค่าการเปิดใช้งานหน่วยอินพุตให้เท่ากับเวกเตอร์อินพุต
Step 4 - คำนวณอินพุตสุทธิของแต่ละหน่วยเอาต์พุต j = 1 to m;
$$ y_ {อันตราย} \: = \: \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 - ใช้ฟังก์ชันการเปิดใช้งานต่อไปนี้เพื่อคำนวณผลลัพธ์
$$ y_ {j} \: = \: f (y_ {อันตราย}) \: = \: \ begin {cases} +1 & if \: y_ {อันตราย} \:> \: 0 \\ 0 & if \ : y_ {อันตราย} \: = \: 0 \\ - 1 & if \: y_ {อันตราย} \: <\: 0 \ end {cases} $$