โครงข่ายประสาทเทียม - Building Blocks
การประมวลผล ANN ขึ้นอยู่กับองค์ประกอบพื้นฐานสามประการต่อไปนี้ -
- โทโพโลยีเครือข่าย
- การปรับน้ำหนักหรือการเรียนรู้
- ฟังก์ชั่นการเปิดใช้งาน
ในบทนี้เราจะพูดถึงรายละเอียดเกี่ยวกับองค์ประกอบทั้งสามของ ANN
โทโพโลยีเครือข่าย
โทโพโลยีเครือข่ายคือการจัดเรียงเครือข่ายพร้อมกับโหนดและสายเชื่อมต่อ ตามโทโพโลยี ANN สามารถจัดเป็นประเภทต่อไปนี้ -
เครือข่าย Feedforward
เป็นเครือข่ายที่ไม่เกิดซ้ำที่มีหน่วยประมวลผล / โหนดในเลเยอร์และโหนดทั้งหมดในเลเยอร์เชื่อมต่อกับโหนดของเลเยอร์ก่อนหน้า การเชื่อมต่อมีน้ำหนักที่แตกต่างกัน ไม่มีลูปป้อนกลับหมายความว่าสัญญาณสามารถไหลไปในทิศทางเดียวเท่านั้นจากอินพุตไปยังเอาต์พุต อาจแบ่งออกเป็นสองประเภทดังต่อไปนี้ -
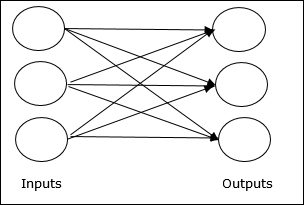
Single layer feedforward network- แนวคิดคือ ANN feedforward ที่มีเลเยอร์ถ่วงน้ำหนักเพียงชั้นเดียว กล่าวอีกนัยหนึ่งเราสามารถพูดได้ว่าเลเยอร์อินพุตเชื่อมต่อกับเลเยอร์เอาต์พุตอย่างสมบูรณ์
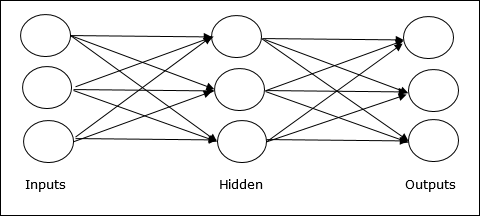
Multilayer feedforward network- แนวคิดคือ ANN feedforward ที่มีเลเยอร์ถ่วงน้ำหนักมากกว่าหนึ่งชั้น เนื่องจากเครือข่ายนี้มีเลเยอร์อย่างน้อยหนึ่งชั้นระหว่างอินพุตและเลเยอร์เอาต์พุตจึงเรียกว่าเลเยอร์ที่ซ่อนอยู่
เครือข่ายข้อเสนอแนะ
ตามชื่อที่แนะนำเครือข่ายป้อนกลับมีเส้นทางป้อนกลับซึ่งหมายความว่าสัญญาณสามารถไหลได้ทั้งสองทิศทางโดยใช้ลูป สิ่งนี้ทำให้เป็นระบบไดนามิกที่ไม่ใช่เชิงเส้นซึ่งเปลี่ยนแปลงไปเรื่อย ๆ จนกว่าจะเข้าสู่สภาวะสมดุล อาจแบ่งออกเป็นประเภทต่างๆดังต่อไปนี้ -
Recurrent networks- เป็นเครือข่ายข้อเสนอแนะที่มีลูปปิด ต่อไปนี้เป็นเครือข่ายที่เกิดซ้ำสองประเภท
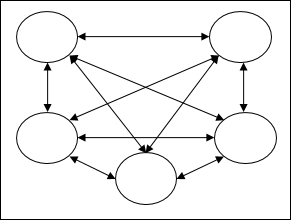
Fully recurrent network - เป็นสถาปัตยกรรมเครือข่ายประสาทเทียมที่ง่ายที่สุดเนื่องจากโหนดทั้งหมดเชื่อมต่อกับโหนดอื่น ๆ ทั้งหมดและแต่ละโหนดทำงานเป็นทั้งอินพุตและเอาต์พุต
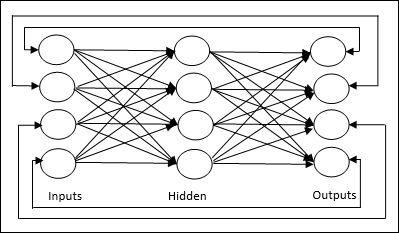
Jordan network - เป็นเครือข่ายวงปิดซึ่งเอาต์พุตจะไปที่อินพุตอีกครั้งเป็นข้อมูลป้อนกลับดังแสดงในแผนภาพต่อไปนี้
การปรับน้ำหนักหรือการเรียนรู้
การเรียนรู้ในโครงข่ายประสาทเทียมเป็นวิธีการปรับเปลี่ยนน้ำหนักของการเชื่อมต่อระหว่างเซลล์ประสาทของเครือข่ายที่ระบุ การเรียนรู้ใน ANN สามารถแบ่งออกเป็นสามประเภท ได้แก่ การเรียนรู้ภายใต้การดูแลการเรียนรู้ที่ไม่มีผู้ดูแลและการเรียนรู้แบบเสริมกำลัง
การเรียนรู้ภายใต้การดูแล
ตามชื่อการเรียนรู้ประเภทนี้ทำภายใต้การดูแลของครู กระบวนการเรียนรู้นี้ขึ้นอยู่กับ
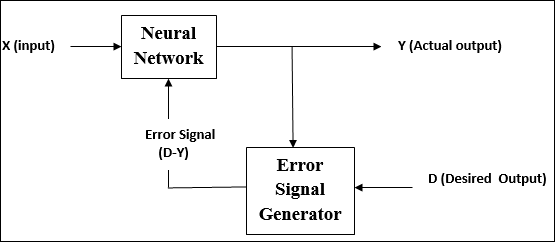
ในระหว่างการฝึกอบรม ANN ภายใต้การเรียนรู้ภายใต้การดูแลเวกเตอร์อินพุตจะถูกนำเสนอไปยังเครือข่ายซึ่งจะให้เวกเตอร์เอาต์พุต เวกเตอร์เอาต์พุตนี้เปรียบเทียบกับเวกเตอร์เอาต์พุตที่ต้องการ สัญญาณข้อผิดพลาดจะถูกสร้างขึ้นหากมีความแตกต่างระหว่างเอาต์พุตจริงและเวกเตอร์เอาต์พุตที่ต้องการ บนพื้นฐานของสัญญาณข้อผิดพลาดนี้น้ำหนักจะถูกปรับจนกว่าเอาต์พุตจริงจะตรงกับเอาต์พุตที่ต้องการ
การเรียนรู้ที่ไม่มีผู้ดูแล
ตามชื่อการเรียนรู้ประเภทนี้ทำได้โดยไม่ต้องอยู่ภายใต้การดูแลของครู กระบวนการเรียนรู้นี้เป็นอิสระ
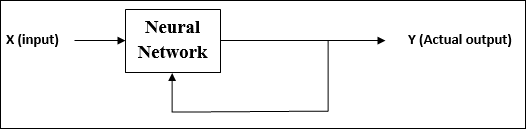
ในระหว่างการฝึกอบรม ANN ภายใต้การเรียนรู้ที่ไม่มีการดูแลจะรวมเวกเตอร์อินพุตประเภทที่คล้ายคลึงกันเพื่อสร้างคลัสเตอร์ เมื่อใช้รูปแบบการป้อนข้อมูลใหม่เครือข่ายประสาทจะให้การตอบสนองของเอาต์พุตที่ระบุคลาสที่เป็นรูปแบบการป้อนข้อมูล
ไม่มีข้อเสนอแนะจากสภาพแวดล้อมว่าอะไรควรเป็นผลลัพธ์ที่ต้องการและถูกต้องหรือไม่ถูกต้อง ดังนั้นในการเรียนรู้ประเภทนี้เครือข่ายจะต้องค้นพบรูปแบบและคุณสมบัติจากข้อมูลอินพุตและความสัมพันธ์ของข้อมูลอินพุตเหนือเอาต์พุต
การเรียนรู้เสริมแรง
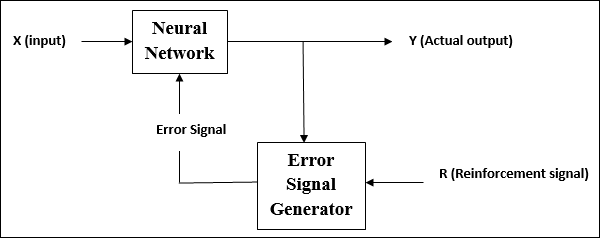
ตามชื่อที่แนะนำการเรียนรู้ประเภทนี้ใช้เพื่อเสริมสร้างหรือเสริมสร้างเครือข่ายผ่านข้อมูลนักวิจารณ์บางอย่าง กระบวนการเรียนรู้นี้คล้ายกับการเรียนรู้ภายใต้การดูแล แต่เราอาจมีข้อมูลน้อยมาก
ในระหว่างการฝึกอบรมเครือข่ายภายใต้การเรียนรู้แบบเสริมแรงเครือข่ายจะได้รับข้อเสนอแนะจากสิ่งแวดล้อม สิ่งนี้ทำให้คล้ายกับการเรียนรู้ภายใต้การดูแล อย่างไรก็ตามข้อเสนอแนะที่ได้รับที่นี่เป็นการประเมินที่ไม่ได้ให้คำแนะนำซึ่งหมายความว่าไม่มีครูในการเรียนรู้ภายใต้การดูแล หลังจากได้รับข้อเสนอแนะเครือข่ายจะทำการปรับน้ำหนักเพื่อรับข้อมูลนักวิจารณ์ที่ดีขึ้นในอนาคต
ฟังก์ชั่นการเปิดใช้งาน
อาจถูกกำหนดให้เป็นแรงพิเศษหรือความพยายามที่ใช้กับอินพุตเพื่อให้ได้เอาต์พุตที่แน่นอน ใน ANN เรายังสามารถใช้ฟังก์ชันการเปิดใช้งานกับอินพุตเพื่อให้ได้ผลลัพธ์ที่แน่นอน ต่อไปนี้เป็นฟังก์ชั่นการเปิดใช้งานที่น่าสนใจ -
ฟังก์ชันการเปิดใช้งานเชิงเส้น
เรียกอีกอย่างว่าฟังก์ชันเอกลักษณ์เนื่องจากไม่มีการแก้ไขอินพุต สามารถกำหนดเป็น -
$$ F (x) \: = \: x $$
ฟังก์ชันการเปิดใช้งาน Sigmoid
มีสองประเภทดังนี้ -
Binary sigmoidal function- ฟังก์ชันการเปิดใช้งานนี้ทำการแก้ไขอินพุตระหว่าง 0 ถึง 1 ซึ่งเป็นค่าบวก มีขอบเขตเสมอซึ่งหมายความว่าเอาต์พุตต้องไม่น้อยกว่า 0 และมากกว่า 1 นอกจากนี้ยังเพิ่มขึ้นอย่างเคร่งครัดตามธรรมชาติซึ่งหมายความว่าอินพุตที่สูงขึ้นจะเป็นเอาต์พุต สามารถกำหนดเป็น
$$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$
Bipolar sigmoidal function- ฟังก์ชันการเปิดใช้งานนี้ทำการแก้ไขอินพุตระหว่าง -1 ถึง 1 ซึ่งอาจเป็นค่าบวกหรือลบก็ได้ มีขอบเขตเสมอซึ่งหมายความว่าเอาต์พุตต้องไม่น้อยกว่า -1 และมากกว่า 1 นอกจากนี้ยังเพิ่มขึ้นอย่างเคร่งครัดในลักษณะเช่นฟังก์ชัน sigmoid สามารถกำหนดเป็น
$$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ frac {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$