การเพิ่มประสิทธิภาพการนูน - Minima และ Maxima
Local Minima หรือ Minimize
$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น minima ท้องถิ่นของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ โดยที่ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึงพื้นที่ใกล้เคียงของ $ \ bar {x} $ เช่น $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึง $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Maxima ท้องถิ่นหรือ Maximizer
$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็นค่าสูงสุดของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ โดยที่ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึงพื้นที่ใกล้เคียงของ $ \ bar {x} $ เช่น $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึง $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
minima ระดับโลก
$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น global minima ของฟังก์ชัน $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ สำหรับ x \ ใน S $
Global maxima
$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น global maxima ของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ สำหรับ x \ ใน S $
ตัวอย่าง
Step 1- ค้นหา minima ในพื้นที่และ maxima ของ $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $
Solution -

จากกราฟของฟังก์ชันข้างต้นเป็นที่ชัดเจนว่า minima ท้องถิ่นเกิดขึ้นที่ $ x = \ pm 2 $ และ local maxima ที่ $ x = 0 $
Step 2- ค้นหา global minima af ฟังก์ชัน $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $
Solution -
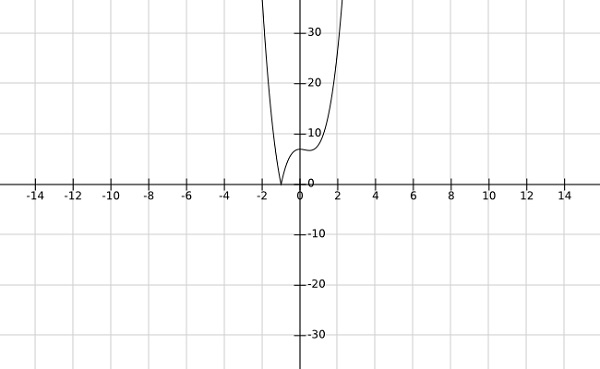
จากกราฟของฟังก์ชันข้างต้นเป็นที่ชัดเจนว่า minima ทั่วโลกเกิดขึ้นที่ $ x = -1 $