การเพิ่มประสิทธิภาพการนูน - คู่มือฉบับย่อ

หลักสูตรนี้มีประโยชน์สำหรับนักเรียนที่ต้องการแก้ปัญหาการเพิ่มประสิทธิภาพแบบไม่เป็นเชิงเส้นที่เกิดขึ้นในงานวิศวกรรมและวิทยาศาสตร์ต่างๆ หลักสูตรนี้เริ่มต้นด้วยทฤษฎีพื้นฐานของการเขียนโปรแกรมเชิงเส้นและจะแนะนำแนวคิดของชุดและฟังก์ชันนูนและคำศัพท์ที่เกี่ยวข้องเพื่ออธิบายทฤษฎีต่างๆที่จำเป็นในการแก้ปัญหาการเขียนโปรแกรมเชิงเส้นที่ไม่ใช่เชิงเส้น หลักสูตรนี้จะแนะนำอัลกอริทึมต่างๆที่ใช้ในการแก้ปัญหาดังกล่าว ปัญหาประเภทนี้เกิดขึ้นในแอปพลิเคชั่นต่างๆรวมถึงการเรียนรู้ของเครื่องปัญหาการเพิ่มประสิทธิภาพในวิศวกรรมไฟฟ้า ฯลฯ นักเรียนต้องมีความรู้มาก่อนเกี่ยวกับแนวคิดและแคลคูลัสทางคณิตศาสตร์ระดับมัธยมศึกษาตอนปลาย

ในหลักสูตรนี้นักเรียนจะได้เรียนรู้วิธีการแก้ปัญหาการเพิ่มประสิทธิภาพเช่น $ min f \ left (x \ right) $ ภายใต้ข้อ จำกัด บางประการ

ปัญหาเหล่านี้แก้ไขได้ง่ายถ้าฟังก์ชัน $ f \ left (x \ right) $ เป็นฟังก์ชันเชิงเส้นและหากข้อ จำกัด เป็นแบบเส้นตรง จากนั้นจะเรียกว่าปัญหาการเขียนโปรแกรมเชิงเส้น (LPP) แต่ถ้าข้อ จำกัด ไม่เป็นเชิงเส้นก็ยากที่จะแก้ปัญหาข้างต้น ถ้าเราไม่สามารถพล็อตฟังก์ชันในกราฟได้ลองวิเคราะห์การเพิ่มประสิทธิภาพอาจเป็นวิธีเดียว แต่เราไม่สามารถลงจุดฟังก์ชันได้หากเกินสามมิติ ดังนั้นจึงมีเทคนิคของการเขียนโปรแกรมแบบไม่เชิงเส้นหรือการเขียนโปรแกรมแบบนูนเพื่อแก้ปัญหาดังกล่าว ในบทช่วยสอนเหล่านี้เราจะมุ่งเน้นไปที่การเรียนรู้เทคนิคดังกล่าวและในท้ายที่สุดอัลกอริทึมบางอย่างเพื่อแก้ปัญหาดังกล่าว ก่อนอื่นเราจะนำแนวคิดของชุดนูนซึ่งเป็นฐานของปัญหาการเขียนโปรแกรมนูน จากนั้นด้วยการแนะนำฟังก์ชันนูนเราจะใช้ทฤษฎีบทที่สำคัญบางประการเพื่อแก้ปัญหาเหล่านี้และอัลกอริทึมบางอย่างตามทฤษฎีเหล่านี้

คำศัพท์

• ช่องว่าง $ \ mathbb {R} ^ n $ - เป็นเวกเตอร์ n มิติที่มีจำนวนจริงกำหนดดังนี้ - $ \ mathbb {R} ^ n = \ left \ {\ left (x_1, x_2, ... , x_n \ right) ^ {\ tau}: x_1, x_2, .... , x_n \ in \ mathbb {R} \ right \} $

• ช่องว่าง $ \ mathbb {R} ^ {mXn} $ - มันคือชุดของเมทริกซ์ค่าจริงทั้งหมดของคำสั่ง $ mXn $

ระเบียบวิธี

Linear Programming เรียกอีกอย่างว่า Linear Optimization เป็นเทคนิคที่ใช้ในการแก้ปัญหาทางคณิตศาสตร์ที่ความสัมพันธ์เป็นแบบเส้นตรง ลักษณะพื้นฐานของ Linear Programming คือการขยายหรือย่อขนาดไฟล์objective function กับบางเรื่อง constraints. ฟังก์ชันวัตถุประสงค์คือฟังก์ชันเชิงเส้นซึ่งได้มาจากแบบจำลองทางคณิตศาสตร์ของปัญหา ข้อ จำกัด คือเงื่อนไขที่กำหนดในแบบจำลองและยังเป็นแบบเชิงเส้น

• จากคำถามที่กำหนดให้ค้นหาฟังก์ชันวัตถุประสงค์
• ค้นหาข้อ จำกัด
• วาดข้อ จำกัด บนกราฟ
• ค้นหาพื้นที่ที่เป็นไปได้ซึ่งเกิดจากจุดตัดของข้อ จำกัด ทั้งหมด
• ค้นหาจุดยอดของพื้นที่ที่เป็นไปได้
• หาค่าของฟังก์ชันวัตถุประสงค์ที่จุดยอดเหล่านี้
• จุดยอดที่ขยายหรือย่อฟังก์ชันวัตถุประสงค์ (ตามคำถาม) คือคำตอบ

ตัวอย่าง

Step 1 - เพิ่มสูงสุด $ 5x + 3y $ ขึ้นอยู่กับ

$ x + y \ leq 2 $,

$ 3x + y \ leq 3 $,

$ x \ geq 0 \: และ \: y \ geq 0 $

Solution -

ขั้นตอนแรกคือการค้นหาพื้นที่ที่เป็นไปได้บนกราฟ

จากกราฟจุดยอดของพื้นที่ที่เป็นไปได้คือ

$ \ left (0, 0 \ right) \ left (0, 2 \ right) \ left (1, 0 \ right) \ left (\ frac {1} {2}, \ frac {3} {2} \ right ) $

ให้ $ f \ left (x, y \ right) = 5x + 3y $

การใส่ค่าเหล่านี้ในฟังก์ชันวัตถุประสงค์เราจะได้ -

$ f \ left (0, 0 \ right) $ = 0

$ f \ left (0, 2 \ right) $ = 6

$ f \ left (1, 0 \ right) $ = 5

$ f \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $ = 7

ดังนั้นฟังก์ชันจะขยายใหญ่สุดที่ $ \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $

Step 2- บริษัท นาฬิกาแห่งหนึ่งผลิตนาฬิกาดิจิตอลและนาฬิกากลไก การคาดการณ์ระยะยาวบ่งบอกถึงความต้องการที่คาดว่าจะมีอย่างน้อย 100 นาฬิกาดิจิตอลและนาฬิกากลไก 80 เรือนในแต่ละวัน เนื่องจากข้อ จำกัด ด้านกำลังการผลิตจึงสามารถผลิตนาฬิการะบบดิจิตอลได้ไม่เกิน 200 เรือนและ 170 เรือนต่อวัน เพื่อให้เป็นไปตามสัญญาการจัดส่งจะมีการจัดส่งนาฬิกาอย่างน้อย 200 เรือนในแต่ละวัน

หากนาฬิกาดิจิตอลแต่ละเรือนขายได้ผลขาดทุน $ \ $ 2 $ แต่นาฬิกากลไกแต่ละเรือนสร้างกำไร $ \ $ 5 $ แต่ละประเภทควรทำรายวันเพื่อเพิ่มผลกำไรสุทธิสูงสุด

Solution -

ให้ $ x $ เป็นจำนวนนาฬิกาดิจิทัลที่ผลิต

$ y $ คือจำนวนนาฬิกากลไกที่ผลิต

ตามคำถามต้องมีนาฬิกาดิจิตอลอย่างน้อย 100 เรือนต่อวันและสามารถผลิตนาฬิกาดิจิตอลได้สูงสุด 200 เรือน

$ \ Rightarrow 100 \ leq \: x \ leq 200 $

ในทำนองเดียวกันจะมีนาฬิกากลไกอย่างน้อย 80 เรือนต่อวันและสามารถผลิตนาฬิกากลไกได้สูงสุด 170 เรือน

$ \ Rightarrow 80 \ leq \: y \ leq 170 $

เนื่องจากต้องผลิตนาฬิกาอย่างน้อย 200 เรือนในแต่ละวัน

$ \ Rightarrow x + y \ leq 200 $

เนื่องจากนาฬิกาดิจิตอลแต่ละเรือนขายได้ผลขาดทุน $ 2 $ แต่นาฬิกากลไกแต่ละเรือนสร้างกำไร $ $ 5 $

กำไรทั้งหมดสามารถคำนวณได้เป็น

กำไร $ = -2x + 5y $

และเราต้องเพิ่มผลกำไรให้สูงสุดดังนั้นจึงสามารถกำหนดคำถามได้ว่า -

เพิ่มสูงสุด $ -2x + 5y $ ขึ้นอยู่กับ

$ 100 \: \ leq x \: \ leq 200 $

$ 80 \: \ leq y \: \ leq 170 $

$ x + y \: \ leq 200 $

การพล็อตสมการข้างต้นในกราฟเราได้

จุดยอดของภูมิภาคที่เป็นไปได้คือ

$ \ left (100, 170 \ right) \ left (200, 170 \ right) \ left (200, 180 \ right) \ left (120, 80 \ right) และ \ left (100, 100 \ right) $

ค่าสูงสุดของฟังก์ชันวัตถุประสงค์จะได้รับที่ $ \ left (100, 170 \ right) $ ดังนั้นในการเพิ่มผลกำไรสุทธิควรผลิตนาฬิกาดิจิตอล 100 เรือนและนาฬิกากลไก 170 หน่วย

บรรทัดฐานคือฟังก์ชันที่ให้ค่าบวกอย่างเคร่งครัดกับเวกเตอร์หรือตัวแปร

Norm คือฟังก์ชัน $ f: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $

ลักษณะพื้นฐานของบรรทัดฐานคือ -

ให้ $ X $ เป็นเวกเตอร์เช่น $ X \ in \ mathbb {R} ^ n $

• $ \ left \ | x \ right \ | \ geq 0 $

• $ \ left \ | x \ right \ | = 0 \ Leftrightarrow x = 0 \ forall x \ ใน X $

• $ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \: x \ ใน X และ \: \ alpha \: คือ \: a \: สเกลาร์ $

• $ \ left \ | x + y \ right \ | \ leq \ left \ | x \ right \ | + \ left \ | ใช่ \ | \ forall x, y \ ใน X $

• $ \ left \ | xy \ right \ | \ geq \ left \ | \ ซ้าย \ | x \ right \ | - \ left \ | ใช่ \ | \ right \ | $

ตามความหมายบรรทัดฐานคำนวณได้ดังนี้ -

• $ \ left \ | x \ right \ | _1 = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ left | x_i \ right | $

• $ \ left \ | x \ right \ | _2 = \ left (\ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ left | x_i \ right | ^ 2 \ right) ^ {\ frac {1} {2}} $

• $ \ left \ | x \ right \ | _p = \ left (\ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ left | x_i \ right | ^ p \ right) ^ {\ frac {1} {p}}, 1 \ leq p \ leq \ infty $

Norm เป็นฟังก์ชันต่อเนื่อง

หลักฐาน

ตามความหมายถ้า $ x_n \ rightarrow x $ ใน $ X \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $ แล้ว $ f \ left (x \ right) $ เป็นฟังก์ชันคงที่

ให้ $ f \ left (x \ right) = \ left \ | x \ right \ | $

ดังนั้น $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = \ left | \ ซ้าย \ | x_n \ right \ | - \ ซ้าย \ | x \ right \ | \ right | \ leq \ left | \ ซ้าย | x_n-x \ right | \: \ right | $

ตั้งแต่ $ x_n \ rightarrow x $ ดังนั้น $ \ left \ | x_n-x \ right \ | \ rightarrow 0 $

ดังนั้น $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | \ leq 0 \ Rightarrow \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = 0 \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $

ดังนั้นบรรทัดฐานจึงเป็นฟังก์ชันต่อเนื่อง

ผลิตภัณฑ์ภายในคือฟังก์ชันที่ให้สเกลาร์กับเวกเตอร์คู่หนึ่ง

ผลิตภัณฑ์ภายใน - $ f: \ mathbb {R} ^ n \ times \ mathbb {R} ^ n \ rightarrow \ kappa $ โดยที่ $ \ kappa $ เป็นสเกลาร์

ลักษณะพื้นฐานของผลิตภัณฑ์ภายในมีดังนี้ -

ให้ $ X \ in \ mathbb {R} ^ n $

• $ \ left \ langle x, x \ right \ rangle \ geq 0, \ forall x \ ใน X $

• $ \ left \ langle x, x \ right \ rangle = 0 \ leftrightarrow x = 0, \ forall x \ ใน X $

• $ \ left \ langle \ alpha x, y \ right \ rangle = \ alpha \ left \ langle x, y \ right \ rangle, \ forall \ alpha \ in \ kappa \: and \: \ forall x, y \ in X $

• $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle, forall x, y, z \ in X $

• $ \ left \ langle \ overline {y, x} \ right \ rangle = \ left (x, y \ right), \ forall x, y \ in X $

Note -

• ความสัมพันธ์ระหว่างบรรทัดฐานและผลิตภัณฑ์ภายใน: $ \ left \ | x \ right \ | = \ sqrt {\ left (x, x \ right)} $

• $ \ forall x, y \ in \ mathbb {R} ^ n, \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n $

ตัวอย่าง

1. ค้นหาผลคูณด้านในของ $ x = \ left (1,2,1 \ right) \: and \: y = \ left (3, -1,3 \ right) $

วิธีการแก้

$ \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + x_3y_3 $

$ \ left \ langle x, y \ right \ rangle = \ left (1 \ times3 \ right) + \ left (2 \ times-1 \ right) + \ left (1 \ times3 \ right) $

$ \ left \ langle x, y \ right \ rangle = 3 + \ left (-2 \ right) + 3 $

$ \ left \ langle x, y \ right \ rangle = 4 $

2. ถ้า $ x = \ left (4,9,1 \ right), y = \ left (-3,5,1 \ right) $ และ $ z = \ left (2,4,1 \ right) $, หา $ \ left (x + y, z \ right) $

วิธีการแก้

ดังที่เราทราบ $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle $

$ \ left \ langle x + y, z \ right \ rangle = \ left (x_1z_1 + x_2z_2 + x_3z_3 \ right) + \ left (y_1z_1 + y_2z_2 + y_3z_3 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = \ left \ {\ left (4 \ times 2 \ right) + \ left (9 \ times 4 \ right) + \ left (1 \ times1 \ right) \ right \} + $

$ \ left \ {\ left (-3 \ times2 \ right) + \ left (5 \ times4 \ right) + \ left (1 \ times 1 \ right) \ right \} $

$ \ left \ langle x + y, z \ right \ rangle = \ left (8 + 36 + 1 \ right) + \ left (-6 + 20 + 1 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = 45 + 15 $

$ \ left \ langle x + y, z \ right \ rangle = 60 $

Local Minima หรือ Minimize

$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น minima ท้องถิ่นของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ โดยที่ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึงพื้นที่ใกล้เคียงของ $ \ bar {x} $ เช่น $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึง $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Maxima ท้องถิ่นหรือ Maximizer

$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็นค่าสูงสุดของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ โดยที่ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึงพื้นที่ใกล้เคียงของ $ \ bar {x} $ เช่น $ N_ \ varepsilon \ left (\ bar {x} \ right) $ หมายถึง $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

minima ระดับโลก

$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น global minima ของฟังก์ชัน $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ สำหรับ x \ ใน S $

Global maxima

$ \ bar {x} \ in \: S $ ถูกกล่าวว่าเป็น global maxima ของฟังก์ชัน $ f $ ถ้า $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ สำหรับ x \ ใน S $

ตัวอย่าง

Step 1- ค้นหา minima ในพื้นที่และ maxima ของ $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $

Solution -

จากกราฟของฟังก์ชันข้างต้นเป็นที่ชัดเจนว่า minima ท้องถิ่นเกิดขึ้นที่ $ x = \ pm 2 $ และ local maxima ที่ $ x = 0 $

Step 2- ค้นหา global minima af ฟังก์ชัน $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $

Solution -

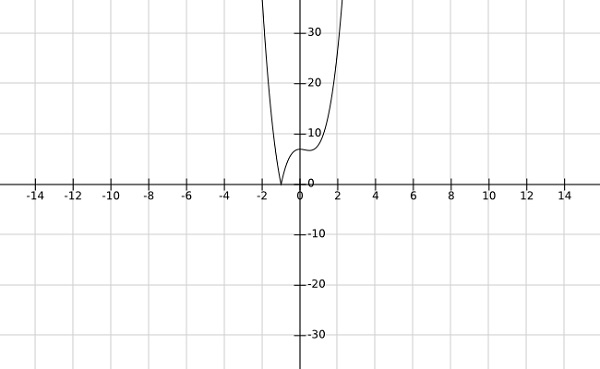
จากกราฟของฟังก์ชันข้างต้นเป็นที่ชัดเจนว่า minima ทั่วโลกเกิดขึ้นที่ $ x = -1 $

ให้ $ S \ subseteq \ mathbb {R} ^ n $ A set S เป็นแบบนูนถ้าส่วนของเส้นตรงที่เชื่อมกับจุดสองจุดใด ๆ ของเซต S ก็เป็นของ S เช่นถ้า $ x_1, x_2 \ ใน S $ แล้ว $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ ใน S $ โดยที่ $ \ lambda \ in \ left (0,1 \ right) $

Note -

• การรวมกันของชุดนูนสองชุดอาจนูนหรือไม่ก็ได้
• จุดตัดของชุดนูนสองชุดจะนูนเสมอกัน

Proof

ให้ $ S_1 $ และ $ S_2 $ เป็นชุดนูนสองชุด

ให้ $ S_3 = S_1 \ cap S_2 $

ให้ $ x_1, x_2 \ ใน S_3 $

ตั้งแต่ $ S_3 = S_1 \ cap S_2 $ ดังนั้น $ x_1, x_2 \ ใน S_1 $ และ $ x_1, x_2 \ ใน S_2 $

เนื่องจาก $ S_i $ เป็นชุดนูน $ \ forall $ i \ ใน 1,2, $

ดังนั้น $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ ใน S_i $ โดยที่ $ \ lambda \ in \ left (0,1 \ right) $

ดังนั้น $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_1 \ cap S_2 $

$ \ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ ใน S_3 $

ดังนั้น $ S_3 $ จึงเป็นชุดนูน

• ค่าเฉลี่ยถ่วงน้ำหนักของรูปแบบ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_ix_i $ โดยที่ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_i = 1 $ และ $ \ lambda_i \ geq 0 , \ forall i \ in \ left [1, k \ right] $ เรียกว่าการรวมรูปกรวยของ $ x_1, x_2, .... x_k. $

• ค่าเฉลี่ยถ่วงน้ำหนักของรูปแบบ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_ix_i $ โดยที่ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_i = 1 $ เรียกว่าชุดค่าผสมของ Affine ของ $ x_1 , x_2, .... x_k. $

• ค่าเฉลี่ยถ่วงน้ำหนักของรูปแบบ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_ix_i $ เรียกว่าค่าผสมเชิงเส้นของ $ x_1, x_2, .... x_k. $

ตัวอย่าง

Step 1 - พิสูจน์ว่าชุด $ S = \ left \ {x \ in \ mathbb {R} ^ n: Cx \ leq \ alpha \ right \} $ เป็นชุดนูน

วิธีการแก้

ให้ $ x_1 $ และ $ x_2 \ ใน S $

$ \ Rightarrow Cx_1 \ leq \ alpha $ และ $ \: และ \: Cx_2 \ leq \ alpha $

แสดง: $ \: \: y = \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ in S \: \ forall \: \ lambda \ in \ left (0,1 \ ขวา) $

$ Cy = C \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = \ lambda Cx_1 + \ left (1- \ lambda \ right) Cx_2 $

$ \ Rightarrow Cy \ leq \ lambda \ alpha + \ left (1- \ lambda \ right) \ alpha $

$ \ Rightarrow Cy \ leq \ alpha $

$ \ Rightarrow y \ ใน S $

ดังนั้น $ S $ จึงเป็นชุดนูน

Step 2 - พิสูจน์ว่าชุด $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} \ leq 8x_2 \ right \} $ เป็นนูน ชุด.

วิธีการแก้

ให้ $ x, y \ ใน S $

ให้ $ x = \ left (x_1, x_2 \ right) $ และ $ y = \ left (y_1, y_2 \ right) $

$ \ Rightarrow x_ {1} ^ {2} \ leq 8x_2 $ และ $ y_ {1} ^ {2} \ leq 8y_2 $

เพื่อแสดง - $ \ lambda x + \ left (1- \ lambda \ right) y \ in S \ Rightarrow \ lambda \ left (x_1, x_2 \ right) + \ left (1- \ lambda \ right) \ left (y_1, y_2 \ right) \ in S \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda) y_2] \ in S \ right) \ right] $

$ ตอนนี้ \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} = \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) x_1y_1 $

แต่ $ 2x_1y_1 \ leq x_ {1} ^ {2} + y_ {1} ^ {2} $

ดังนั้น,

$ \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) \ left (x_ {1} ^ {2} + y_ {1} ^ {2} \ right) $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda x_ {1} ^ {2} + \ left (1- \ lambda \ right) y_ {1} ^ {2} $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ lambda x_2 + 8 \ left (1- \ lambda \ right) y_2 $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ left [\ lambda x_2 + \ left (1- \ lambda \ right) y_2 \ right] $

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) y \ ใน S $

Step 3 - แสดงว่าชุด $ S \ in \ mathbb {R} ^ n $ นูนก็ต่อเมื่อสำหรับแต่ละจำนวนเต็ม k การรวมกันนูนของ k จุดใด ๆ ของ $ S $ อยู่ใน $ S $

วิธีการแก้

ให้ $ S $ เป็นชุดนูน จากนั้นเพื่อแสดง;

$ c_1x_1 + c_2x_2 + ..... + c_kx_k \ ใน S, \ displaystyle \ sum \ LIMIT_ {1} ^ k c_i = 1, c_i \ geq 0, \ forall i \ ใน 1,2, .... , k $

พิสูจน์โดยการเหนี่ยวนำ

สำหรับ $ k = 1, x_1 \ ใน S, c_1 = 1 \ Rightarrow c_1x_1 \ ใน S $

สำหรับ $ k = 2, x_1, x_2 \ in S, c_1 + c_2 = 1 $ และเนื่องจาก S เป็นชุดนูน

$ \ Rightarrow c_1x_1 + c_2x_2 \ ใน S. $

ให้จุดรวมนูนของจุด m ของ S อยู่ใน S คือ

$ c_1x_1 + c_2x_2 + ... + c_mx_m \ ใน S, \ displaystyle \ sum \ LIMIT_ {1} ^ m c_i = 1, c_i \ geq 0, \ forall i \ ใน 1,2, ... , m $

ตอนนี้ให้ $ x_1, x_2 .... , x_m, x_ {m + 1} \ ใน S $

ให้ $ x = \ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m + \ mu_ {m + 1} x_ {m + 1} $

ให้ $ x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} + \ mu_ {m + 1} x_ {m + 1} $

ให้ $ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} $

$ \ Rightarrow x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) y + \ mu_ {m + 1} x_ {m + 1} $

ตอนนี้ $ y \ ใน S $ เพราะผลรวมของ coe ff icients คือ 1

$ \ Rightarrow x \ ใน S $ เนื่องจาก S เป็นชุดนูนและ $ y, x_ {m + 1} \ ใน S $

ดังนั้นจึงพิสูจน์ได้โดยการเหนี่ยวนำ

ชุด $ A $ ถูกกล่าวว่าเป็นชุด Affine ถ้าสำหรับจุดสองจุดที่แตกต่างกันเส้นที่ผ่านจุดเหล่านี้จะอยู่ในชุด $ A $

Note -

• $ S $ เป็นชุด Affine ก็ต่อเมื่อมีการรวมกันของคะแนน

• ชุดว่างเปล่าและชุดเดี่ยวมีทั้งชุดแบบสัมพันธ์และชุดนูน

  ตัวอย่างเช่นการแก้ปัญหาของสมการเชิงเส้นคือเซต Affine

หลักฐาน

ให้ S เป็นคำตอบของสมการเชิงเส้น

ตามคำนิยาม $ S = \ left \ {x \ in \ mathbb {R} ^ n: Ax = b \ right \} $

ให้ $ x_1, x_2 \ in S \ Rightarrow Ax_1 = b $ และ $ Ax_2 = b $

เพื่อพิสูจน์: $ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = b, \ forall \ theta \ in \ left (0,1 \ right) $

$ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = \ theta Ax_1 + \ left (1- \ theta \ right) Ax_2 = \ theta b + \ left (1- \ theta \ right ) b = b $

ดังนั้น S จึงเป็นเซตของ Affine

ทฤษฎีบท

ถ้า $ C $ เป็นเซต Affine และ $ x_0 \ ใน C $ ดังนั้นเซต $ V = C-x_0 = \ left \ {x-x_0: x \ in C \ right \} $ คือซับสเปซของ C

หลักฐาน

ให้ $ x_1, x_2 \ ใน V $

ที่จะแสดง: $ \ alpha x_1 + \ beta x_2 \ ใน V $ สำหรับ $ \ alpha, \ beta $

ตอนนี้ $ x_1 + x_0 \ ใน C $ และ $ x_2 + x_0 \ ใน C $ ตามคำจำกัดความของ V

ตอนนี้ $ \ alpha x_1 + \ beta x_2 + x_0 = \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 $

แต่ $ \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 \ ใน C $ เพราะ C เป็นชุด Affine .

ดังนั้น $ \ alpha x_1 + \ beta x_2 \ ใน V $

ดังนั้นจึงพิสูจน์แล้ว

ตัวถังนูนของชุดจุดใน S คือขอบเขตของส่วนนูนที่เล็กที่สุดซึ่งมีจุดทั้งหมดของ S อยู่ภายในหรือบนขอบเขตของมัน

หรือ

ให้ $ S \ subseteq \ mathbb {R} ^ n $ ตัวนูนของ S ซึ่งแสดงว่า $ Co \ left (S \ right) $ by คือชุดของชุดค่าผสมนูนทั้งหมดของ S นั่นคือ $ x \ in Co \ left (S \ right) $ if and only if $ x \ in \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_ix_i $ โดยที่ $ \ displaystyle \ sum \ LIMIT_ {1} ^ n \ lambda_i = 1 $ และ $ \ lambda_i \ geq 0 \ forall x_i \ ใน S $

Remark - การสร้างฮัลล์ของชุดของจุดใน S ในระนาบกำหนดรูปหลายเหลี่ยมนูนและจุดของ S บนขอบเขตของรูปหลายเหลี่ยมจะกำหนดจุดยอดของรูปหลายเหลี่ยม

Theorem $ Co \ left (S \ right) = \ left \ {x: x = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_ix_i, x_i \ in S, \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 \ right \} $ แสดงว่าตัวถังนูนเป็นชุดนูน

หลักฐาน

ให้ $ x_1, x_2 \ in Co \ left (S \ right) $ แล้ว $ x_1 = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_ix_i $ และ $ x_2 = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_ \ gamma x_i $ โดยที่ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 $ และ $ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ gamma_i = 1, \ gamma_i \ geq0 $

สำหรับ $ \ theta \ in \ left (0,1 \ right), \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ theta \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_ix_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ gamma_ix_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ lambda_i \ theta x_i + \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ gamma_i \ ซ้าย (1- \ theta \ right) x_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ ขวา] x_i $

พิจารณาค่าสัมประสิทธิ์

$ \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ right] = \ theta \ displaystyle \ sum \ LIMIT_ {i = 1 } ^ n \ lambda_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ LIMIT_ {i = 1} ^ n \ gamma_i = \ theta + \ left (1- \ theta \ right) = 1 $

ดังนั้น $ \ theta x_1 + \ left (1- \ theta \ right) x_2 \ in Co \ left (S \ right) $

ดังนั้นตัวถังนูนจึงเป็นชุดนูน

ให้ S เป็นชุดโดยพลการใน $ \ mathbb {R} ^ n $ ถ้า $ x \ in Co \ left (S \ right) $ แล้ว $ x \ in Co \ left (x_1, x_2, .... , x_n, x_ {n + 1} \ right) $.

หลักฐาน

ตั้งแต่ $ x \ in Co \ left (S \ right) $ ดังนั้น $ x $ จึงถูกแทนด้วยการรวมกันของจำนวนจุด จำกัด ใน S นั่นคือ

$ x = \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ lambda_jx_j, \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ lambda_j = 1, \ lambda_j \ geq 0 $ และ $ x_j \ in S, \ forall j \ in \ left (1, k \ right) $

ถ้า $ k \ leq n + 1 $ ผลลัพธ์ที่ได้จะเป็นจริงอย่างชัดเจน

ถ้า $ k \ geq n + 1 $ ดังนั้น $ \ left (x_2-x_1 \ right) \ left (x_3-x_1 \ right), ..... , \ left (x_k-x_1 \ right) $ จะขึ้นอยู่กับเชิงเส้น .

$ \ Rightarrow \ มีอยู่ \ mu _j \ in \ mathbb {R}, 2 \ leq j \ leq k $ (ไม่ใช่ศูนย์ทั้งหมด) เช่น $ \ displaystyle \ sum \ LIMIT_ {j = 2} ^ k \ mu _j \ left (x_j-x_1 \ right) = 0 $

กำหนด $ \ mu_1 = - \ displaystyle \ sum \ LIMIT_ {j = 2} ^ k \ mu _j $ แล้ว $ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ mu_j x_j = 0, \ displaystyle \ sum \ Limit_ {j = 1} ^ k \ mu_j = 0 $

โดยที่ $ ของ $ \ mu_j ไม่ใช่ทั้งหมดจะเท่ากับศูนย์ ตั้งแต่ $ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ mu_j = 0 $ อย่างน้อยหนึ่งใน $ \ mu_j> 0,1 \ leq j \ leq k $

จากนั้น $ x = \ displaystyle \ sum \ LIMIT_ {1} ^ k \ lambda_j x_j + 0 $

$ x = \ displaystyle \ sum \ LIMIT_ {1} ^ k \ lambda_j x_j- \ alpha \ displaystyle \ sum \ LIMIT_ {1} ^ k \ mu_j x_j $

$ x = \ displaystyle \ sum \ LIMIT_ {1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $

เลือก $ \ alpha $ ให้ $ \ alpha = min \ left \ {\ frac {\ lambda_j} {\ mu_j}, \ mu_j \ geq 0 \ right \} = \ frac {\ lambda_j} {\ mu _j}, $ สำหรับบาง $ i = 1,2, ... , k $

ถ้า $ \ mu_j \ leq 0, \ lambda_j- \ alpha \ mu_j \ geq 0 $

ถ้า $ \ mu_j> 0 แล้ว \: \ frac {\ lambda _j} {\ mu_j} \ geq \ frac {\ lambda_i} {\ mu _i} = \ alpha \ Rightarrow \ lambda_j- \ alpha \ mu_j \ geq 0, j = 1,2, ... k $

โดยเฉพาะ $ \ lambda_i- \ alpha \ mu_i = 0 $ ตามคำจำกัดความของ $ \ alpha $

$ x = \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $ โดยที่

$ \ lambda_j- \ alpha \ mu_j \ geq0 $ และ $ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) = 1 $ และ $ \ lambda_i- \ alpha \ mu_i = 0 $

ดังนั้นจึงสามารถแทนค่า x เป็นการรวมกันของจุดสูงสุด (k-1) ได้

กระบวนการลดนี้สามารถทำซ้ำได้จนกว่า x จะแสดงเป็นการรวมกันขององค์ประกอบ (n + 1)

ให้ S เป็นเซตที่ไม่ว่างเปล่าปิดและมีขอบเขต (เรียกอีกอย่างว่าเซตคอมแพ็ค) ใน $ \ mathbb {R} ^ n $ และให้ $ f: S \ rightarrow \ mathbb {R} $ เป็นฟังก์ชันต่อเนื่องบน S จากนั้น ปัญหาขั้นต่ำ $ \ left \ {f \ left (x \ right): x \ in S \ right \} $ บรรลุขั้นต่ำ

หลักฐาน

เนื่องจาก S ไม่ว่างเปล่าและมีขอบเขตจึงมีขอบเขตล่าง

$ \ alpha = Inf \ left \ {f \ left (x \ right): x \ in S \ right \} $

ตอนนี้ให้ $ S_j = \ left \ {x \ in S: \ alpha \ leq f \ left (x \ right) \ leq \ alpha + \ delta ^ j \ right \} \ forall j = 1,2, ... $ และ $ \ delta \ in \ left (0,1 \ right) $

ตามคำจำกัดความของ infimium $ S_j $ ไม่ว่างสำหรับแต่ละ $ j $

เลือก $ x_j \ ใน S_j $ เพื่อรับลำดับ $ \ left \ {x_j \ right \} $ สำหรับ $ j = 1,2, ... $

เนื่องจาก S ถูกล้อมรอบลำดับจึงถูกล้อมรอบด้วยและมีการบรรจบกันในภายหลัง $ \ left \ {y_j \ right \} $ ซึ่งมาบรรจบกันเป็น $ \ hat {x} $ ดังนั้น $ \ hat {x} $ จึงเป็นจุด จำกัด และ S ถูกปิดดังนั้น $ \ hat {x} \ ใน S $ เนื่องจาก f ต่อเนื่อง $ f \ left (y_i \ right) \ rightarrow f \ left (\ hat {x} \ right) $

ตั้งแต่ $ \ alpha \ leq f \ left (y_i \ right) \ leq \ alpha + \ delta ^ k, \ alpha = \ displaystyle \ lim_ {k \ rightarrow \ infty} f \ left (y_i \ right) = f \ left ( \ หมวก {x} \ right) $

ดังนั้น $ \ hat {x} $ จึงเป็นวิธีการลดขนาด

หมายเหตุ

มีเงื่อนไขที่จำเป็นที่สำคัญสองประการสำหรับ Weierstrass Theorem มีดังต่อไปนี้ -

• Step 1 - เซต S ควรเป็นเซตที่มีขอบเขต

  พิจารณาฟังก์ชัน f \ left (x \ right) = x $

  เป็นชุดที่ไม่ถูกผูกไว้และมี minima ที่จุดใดก็ได้ในโดเมน

  ดังนั้นสำหรับ minima ที่จะได้รับ S ควรถูกล้อมรอบ

• Step 2 - ควรปิดชุด S

  พิจารณาฟังก์ชัน $ f \ left (x \ right) = \ frac {1} {x} $ ในโดเมน \ left (0,1 \ right)

  ฟังก์ชันนี้ไม่ได้ถูกปิดในโดเมนที่กำหนดและไม่มี minima ด้วย

  ดังนั้นสำหรับ minima ที่จะได้รับ S ควรปิด

ให้ S เป็นชุดนูนปิดที่ไม่ว่างเปล่าใน $ \ mathbb {R} ^ n $ และให้ $ y \ notin S $ จากนั้น $ \ มีอยู่ $ a point $ \ bar {x} \ ใน S $ โดยมีระยะห่างต่ำสุดจาก y เช่น $ \ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ ใน S. $

นอกจากนี้ $ \ bar {x} $ ยังเป็นจุดที่ลดขนาดลงก็ต่อเมื่อ $ \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $ หรือ $ \ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0 $

หลักฐาน

การดำรงอยู่ของจุดที่ใกล้เคียงที่สุด

เนื่องจาก $ S \ ne \ phi มี $ a point $ \ hat {x} \ ใน S $ ดังนั้นระยะทางต่ำสุดของ S จาก y น้อยกว่าหรือเท่ากับ $ \ left \ | y- \ hat {x} \ right \ | $.

กำหนด $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $

เนื่องจาก $ \ hat {S} $ ถูกปิดและมีขอบเขตและเนื่องจากบรรทัดฐานเป็นฟังก์ชันต่อเนื่องดังนั้นตามทฤษฎีบทของ Weierstrass จึงมีจุดต่ำสุด $ \ hat {x} \ ใน S $ ซึ่งเท่ากับ $ \ left \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |, x \ ใน S \ right \} $

ความเป็นเอกลักษณ์

สมมติว่า $ \ bar {x} \ ใน S $ เช่นนั้น $ \ left \ | y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $

เนื่องจาก S มีความนูน $ \ frac {\ hat {x} + \ bar {x}} {2} \ ใน S $

แต่ $ \ left \ | y- \ frac {\ hat {x} - \ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $

ไม่สามารถเป็นอสมการที่เข้มงวดได้เนื่องจาก $ \ hat {x} $ ใกล้เคียงกับ y มากที่สุด

ดังนั้น $ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ | $ สำหรับบาง $ \ mu $

ตอนนี้ $ \ left \ | \ mu \ right \ | = 1. $ ถ้า $ \ mu = -1 $ แล้ว $ \ left (y- \ hat {x} \ right) = - \ left (y- \ hat {x} \ right) \ Rightarrow y = \ frac {\ hat {x} + \ bar {x}} {2} \ ใน S $

แต่ $ y \ ใน S $ ดังนั้นความขัดแย้ง ดังนั้น $ \ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $

ดังนั้นการย่อจุดจึงไม่เหมือนใคร

สำหรับส่วนที่สองของการพิสูจน์ให้สมมติว่า $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0 $ สำหรับ $ x ทั้งหมดทั้งหมด ใน S $

ตอนนี้

$ \ left \ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} +2 \ left (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $ เพราะ $ \ left \ | \ หมวก {x} -x \ right \ | ^ {2} \ geq 0 $ และ $ \ left (\ hat {x} - x \ right) ^ {T} \ left (y- \ hat {x} \ right ) \ geq 0 $

ดังนั้น $ \ hat {x} $ จึงเป็นจุดที่ลดลง

ในทางกลับกันสมมติว่า $ \ hat {x} $ คือ minimizimg point

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ ใน S $

เนื่องจาก S เป็นชุดนูน

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ ใน S $ สำหรับ $ x \ ใน S $ และ $ \ lambda \ in \ left (0,1 \ right) $

ตอนนี้ $ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $

และ

$ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $

ดังนั้นพิสูจน์แล้ว

ให้ S เป็นค่านูนปิดที่ไม่ว่างเปล่าตั้งค่าเป็น $ \ mathbb {R} ^ n $ และ $ y \ notin S $ จากนั้นมีเวกเตอร์ที่ไม่ใช่ศูนย์ $ p $ และสเกลาร์ $ \ beta $ เช่น $ p ^ T y> \ beta $ และ $ p ^ T x <\ beta $ สำหรับแต่ละ $ x \ ใน S $

หลักฐาน

เนื่องจาก S ไม่ใช่ชุดนูนปิดที่ว่างเปล่าและ $ y \ notin S $ ด้วยทฤษฎีบทจุดที่ใกล้เคียงที่สุดจึงมีจุดย่อเฉพาะ $ \ hat {x} \ ใน S $ เช่นนั้น

$ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ ใน S $

ให้ $ p = \ left (y- \ hat {x} \ right) \ neq 0 $ และ $ \ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T \ หมวก {x} $.

จากนั้น $ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right) $ i, e., $ p ^ Tx \ leq \ beta $

นอกจากนี้ $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right) $

$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $

$ \ Rightarrow p ^ Ty> \ beta $

ทฤษฎีบทนี้ส่งผลให้แยกไฮเปอร์เพลน ไฮเปอร์เพลนตามทฤษฎีบทข้างต้นสามารถกำหนดได้ดังนี้ -

ให้ $ S_1 $ และ $ S_2 $ เป็นชุดย่อยที่ไม่ว่างเปล่าของ $ \ mathbb {R} $ และ $ H = \ left \ {X: A ^ TX = b \ right \} $ เป็นไฮเปอร์เพลน

• ไฮเปอร์เพลน H ถูกกล่าวว่าจะแยก $ S_1 $ และ $ S_2 $ ถ้า $ A ^ TX \ leq b \ forall X \ ใน S_1 $ และ $ A_TX \ geq b \ forall X \ ใน S_2 $

• ไฮเปอร์เพลน H ถูกกล่าวว่าแยก $ S_1 $ และ $ S_2 $ อย่างเคร่งครัดหาก $ A ^ TX <b \ forall X \ ใน S_1 $ และ $ A_TX> b \ forall X \ ใน S_2 $

• กล่าวกันว่าไฮเปอร์เพลน H จะแยก $ S_1 $ และ $ S_2 $ อย่างชัดเจนหาก $ A ^ TX \ leq b \ forall X \ ใน S_1 $ และ $ A_TX \ geq b + \ varepsilon \ forall X \ ใน S_2 $ โดยที่ $ \ varepsilon $ เป็นสเกลาร์ที่เป็นบวก

ชุดที่ไม่ว่างเปล่า C ใน $ \ mathbb {R} ^ n $ ถูกกล่าวว่าเป็นรูปกรวยที่มีจุดยอด 0 ถ้า $ x \ ใน C \ Rightarrow \ lambda x \ ใน C \ forall \ lambda \ geq 0 $

ชุด C เป็นรูปกรวยนูนถ้านูนเช่นเดียวกับกรวย

ตัวอย่างเช่น $ y = \ left | x \ right | $ ไม่ใช่กรวยนูนเพราะมันไม่นูน

แต่ $ y \ geq \ left | x \ right | $ เป็นรูปกรวยนูนเนื่องจากมีลักษณะนูนเช่นเดียวกับกรวย

Note - กรวย C จะนูนก็ต่อเมื่อมีค่า $ x, y \ in C, x + y \ ใน C $ เท่านั้น

หลักฐาน

เนื่องจาก C เป็นรูปกรวยสำหรับ $ x, y \ ใน C \ Rightarrow \ lambda x \ ใน C $ และ $ \ mu y \ ใน C \: \ forall \: \ lambda, \ mu \ geq 0 $

C จะนูนถ้า $ \ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right) $

เนื่องจาก C เป็นรูปกรวย $ \ lambda x \ ใน C $ และ $ \ left (1- \ lambda \ right) y \ in C \ Leftrightarrow x, y \ ใน C $

ดังนั้น C จะนูนถ้า $ x + y \ ใน C $

โดยทั่วไปถ้า $ x_1, x_2 \ ใน C $ ดังนั้น $ \ lambda_1x_1 + \ lambda_2x_2 \ ใน C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $

ตัวอย่าง

• การรวมรูปกรวยของเซตเวกเตอร์อนันต์ใน $ \ mathbb {R} ^ n $ คือกรวยนูน

• ชุดว่างใด ๆ คือกรวยนูน

• ฟังก์ชันเชิงเส้นใด ๆ คือกรวยนูน

• เนื่องจากไฮเปอร์เพลนเป็นแบบเส้นตรงจึงเป็นรูปกรวยนูนด้วย

• ช่องว่างครึ่งปิดเป็นกรวยนูน

Note - จุดตัดของกรวยนูนสองอันคือกรวยนูน แต่การรวมกันอาจเป็นหรือไม่เป็นกรวยนูนก็ได้

ให้ S เป็นเซตที่ไม่ว่างใน $ \ mathbb {R} ^ n $ จากนั้นกรวยเชิงขั้วของ S ที่แสดงด้วย $ S ^ * $ จะได้รับโดย $ S ^ * = \ left \ {p \ in \ mathbb {R } ^ n, p ^ Tx \ leq 0 \: \ forall x \ ใน S \ right \} $

ข้อสังเกต

• กรวยโพลาร์จะนูนเสมอแม้ว่า S จะไม่นูนก็ตาม

• ถ้า S เป็นเซตว่าง $ S ^ * = \ mathbb {R} ^ n $

• ขั้วอาจถูกมองว่าเป็นลักษณะทั่วไปของมุมฉาก

ให้ $ C \ subseteq \ mathbb {R} ^ n $ ตามด้วยสเปซมุมฉากของ C แสดงด้วย $ C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ ใน C \ right \} $

เลมมา

ให้ $ S, S_1 $ และ $ S_2 $ เป็นชุดที่ไม่ว่างใน $ \ mathbb {R} ^ n $ ดังนั้นข้อความต่อไปนี้จะเป็นจริง -

• $ S ^ * $ เป็นกรวยนูนปิด

• $ S \ subseteq S ^ {**} $ โดยที่ $ S ^ {**} $ เป็นรูปกรวยเชิงขั้วของ $ S ^ * $

• $ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $

หลักฐาน

Step 1 - $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \} $

• ให้ $ x_1, x_2 \ ใน S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ และ $ x_ {2} ^ {T} x \ leq 0, \ forall x \ ใน S $

  สำหรับ $ \ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ ใน S $

  $ = \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0 $

  ดังนั้น $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ ใน S ^ * $

  ดังนั้น $ S ^ * $ จึงเป็นชุดนูน

• สำหรับ $ \ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ ใน S $

  ดังนั้น $ \ lambda p ^ T x \ leq 0, $

  $ \ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0 $

  $ \ Rightarrow \ lambda p \ ใน S ^ * $

  ดังนั้น $ S ^ * $ จึงเป็นรูปกรวย

• หากต้องการแสดง $ S ^ * $ ถูกปิดกล่าวคือเพื่อแสดงว่า $ p_n \ rightarrow p $ เป็น $ n \ rightarrow \ infty $ แล้ว $ p \ ใน S ^ * $

  $ \ forall x \ ใน S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x $

  เป็น $ p_n \ rightarrow p $ เป็น $ n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $

  ดังนั้น $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x $ แต่ $ p_ {n} ^ {T} x \ leq 0, \: \ forall x \ ใน S $

  ดังนั้น $ p ^ Tx \ leq 0, \ forall x \ ใน S $

  $ \ Rightarrow p \ ใน S ^ * $

  ดังนั้น $ S ^ * $ จึงปิด

Step 2 - $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \} $

ให้ $ x \ ใน S $ แล้ว $ \ forall p \ ใน S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ ใน S ^ {**} $

ดังนั้น $ S \ subseteq S ^ {**} $

Step 3 - $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ ใน S_2 \ right \} $

ตั้งแต่ $ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ ใน S_2 \ Rightarrow \ forall x \ ใน S_1 $

ดังนั้นถ้า $ \ hat {p} \ ใน S_2 ^ *, $ แล้ว $ \ hat {p} ^ Tx \ leq 0, \ forall x \ ใน S_2 $

$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ ใน S_1 $

$ \ Rightarrow \ hat {p} ^ T \ ใน S_1 ^ * $

$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $

ทฤษฎีบท

ให้ C เป็นกรวยนูนปิดที่ไม่ว่างเปล่าแล้ว $ C = C ^ ** $

หลักฐาน

$ C = C ^ {**} $ โดยคำย่อก่อนหน้า

เพื่อพิสูจน์: $ x \ in C ^ {**} \ subseteq C $

ให้ $ x \ in C ^ {**} $ และให้ $ x \ notin C $

จากนั้นด้วยทฤษฎีบทการแบ่งแยกพื้นฐานมีเวกเตอร์ $ p \ neq 0 $ และสเกลาร์ $ \ alpha $ ดังกล่าวที่ $ p ^ Ty \ leq \ alpha, \ forall y \ ใน C $

ดังนั้น $ p ^ Tx> \ alpha $

แต่ตั้งแต่ $ \ left (y = 0 \ right) \ ใน C $ และ $ p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0 $ และ $ p ^ Tx> 0 $

ถ้า $ p \ notin C ^ * $ แสดงว่ามี $ \ bar {y} \ อยู่ใน C $ เช่น $ p ^ T \ bar {y}> 0 $ และ $ p ^ T \ left (\ lambda \ bar {y} \ right) $ สามารถทำให้ใหญ่ได้ตามอำเภอใจโดยรับ $ \ lambda $ ให้ใหญ่พอสมควร

สิ่งนี้ขัดแย้งกับข้อเท็จจริงที่ว่า $ p ^ Ty \ leq \ alpha, \ forall y \ ใน C $

ดังนั้น $ p \ ใน C ^ * $

ตั้งแต่ $ x \ in C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $

ดังนั้น $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $

แต่ $ p ^ Tx> \ alpha $

ดังนั้นจึงเป็นความขัดแย้ง

ดังนั้น $ x \ ใน C $

ดังนั้น $ C = C ^ {**} $

จุดของรูปแบบ $ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n $ กับ $ \ alpha_1, \ alpha_2, ... , \ alpha_n \ geq 0 $ เรียกว่าการรวมรูปกรวยของ $ x_1, x_2, ... , x_n. $

• ถ้า $ x_i $ อยู่ในกรวยนูน C การรวมรูปกรวยของ $ x_i $ จะอยู่ใน C ด้วย

• ชุด C เป็นรูปกรวยนูนหากมีการรวมกันขององค์ประกอบรูปกรวยทั้งหมด

Conic Hull

รูปกรวยถูกกำหนดให้เป็นชุดของการรวมรูปกรวยทั้งหมดของเซต S ที่กำหนดและแสดงด้วย coni (S)

ดังนั้น $ coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ LIMIT_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ right \} $

• ตัวถังรูปกรวยเป็นชุดนูน
• ต้นกำเนิดมักเป็นของตัวถังรูปกรวย

ชุดใน $ \ mathbb {R} ^ n $ ถูกกล่าวว่าเป็นรูปหลายเหลี่ยมถ้ามันเป็นจุดตัดของจำนวน จำกัด ของช่องว่างครึ่งปิดนั่นคือ

$ S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, .... , n \ right \} $

ตัวอย่างเช่น,

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \} $

กรวยหลายเหลี่ยม

ชุดใน $ \ mathbb {R} ^ n $ จะกล่าวว่าเป็นรูปกรวยหลายเหลี่ยมถ้ามันเป็นจุดตัดของจำนวนช่องว่างครึ่งหนึ่งที่มีจุดเริ่มต้นนั่นคือ $ S = \ left \ {x \ in \ mathbb { R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \} $

Polytope

polytope คือชุดรูปหลายเหลี่ยมซึ่งมีขอบเขต

หมายเหตุ

• polytope คือเปลือกนูนของชุดจุดที่ จำกัด
• กรวยรูปหลายเหลี่ยมถูกสร้างขึ้นโดยชุดเวกเตอร์ที่ จำกัด
• ชุดรูปหลายเหลี่ยมเป็นชุดปิด
• ชุดรูปหลายเหลี่ยมคือชุดนูน

ให้ S เป็นชุดนูนใน $ \ mathbb {R} ^ n $ เวกเตอร์ $ x \ ใน S $ ถูกกล่าวว่าเป็นจุดสุดขั้วของ S ถ้า $ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ กับ $ x_1, x_2 \ ใน S $ และ $ \ lambda \ ใน \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $

ตัวอย่าง

Step 1 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $

จุดสุดขั้ว $ E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $

Step 2 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $

จุดสุดขั้ว $ E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \} $

Step 3 - S คือ polytope ที่สร้างโดยจุด $ \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2, 4 \ right) \ left (0,2 \ right) \ right \} $

จุดสุดขีด $ E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ right \} $

หมายเหตุ

• จุดใด ๆ ของชุดนูน S สามารถแสดงเป็นจุดรวมนูนของจุดสุดขั้ว

• เป็นจริงสำหรับเซตปิดและมีขอบเขตใน $ \ mathbb {R} ^ n $ เท่านั้น

• อาจไม่เป็นความจริงสำหรับชุดที่ไม่ถูกผูกไว้

k คะแนนมาก

จุดในชุดนูนเรียกว่า k สุดโต่งถ้าเป็นจุดภายในของชุดนูน k มิติภายใน S และไม่ใช่จุดภายในของ a (k + 1) - มิตินูนที่กำหนดภายใน S โดยทั่วไปสำหรับชุดนูน S จุดสุดขั้ว k จะทำให้ใบหน้าเปิดมิติ k

ให้ S เป็นชุดนูนปิดใน $ \ mathbb {R} ^ n $ เวกเตอร์ที่ไม่ใช่ศูนย์ $ d \ in \ mathbb {R} ^ n $ เรียกว่าทิศทางของ S ถ้าสำหรับแต่ละ $ x \ in S, x + \ lambda d \ in S, \ forall \ lambda \ geq 0. $

• สองทิศทาง $ d_1 $ และ $ d_2 $ ของ S เรียกว่าแตกต่างกันถ้า $ d \ neq \ alpha d_2 $ สำหรับ $ \ alpha> 0 $

• ทิศทาง $ d $ ของ $ S $ ถูกกล่าวว่าเป็นทิศทางที่รุนแรงหากไม่สามารถเขียนเป็นการรวมเชิงเส้นเชิงบวกของสองทิศทางที่แตกต่างกันกล่าวคือถ้า $ d = \ lambda _1d_1 + \ lambda _2d_2 $ สำหรับ $ \ lambda _1, \ lambda _2> 0 $ แล้ว $ d_1 = \ alpha d_2 $ สำหรับ $ \ alpha $

• ทิศทางอื่น ๆ สามารถแสดงเป็นส่วนผสมเชิงบวกของทิศทางที่รุนแรง

• สำหรับชุดนูน $ S $ ทิศทาง d เช่น $ x + \ lambda d \ ใน S $ สำหรับ $ x \ ใน S $ และ $ \ lambda \ geq0 $ ทั้งหมดเรียกว่า recessive ในราคา $ S $

• ให้ E เป็นชุดของจุดที่ฟังก์ชันหนึ่ง $ f: S \ rightarrow $ เหนือชุดนูนที่ไม่ว่างเปล่า S ใน $ \ mathbb {R} ^ n $ ถึงจุดสูงสุดแล้ว $ E $ เรียกว่าหน้าสัมผัสของ $ S $. ทิศทางของใบหน้าที่เปิดเผยเรียกว่าทิศทางที่เปิดเผย

• รังสีที่มีทิศทางไปในทิศทางที่รุนแรงเรียกว่ารังสีเอกซ์

ตัวอย่าง

พิจารณาฟังก์ชัน $ f \ left (x \ right) = y = \ left | x \ right | $ โดยที่ $ x \ in \ mathbb {R} ^ n $ ให้ d เป็นเวกเตอร์หน่วยใน $ \ mathbb {R} ^ n $

จากนั้น d คือทิศทางสำหรับฟังก์ชัน f เพราะสำหรับ $ \ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right) $

ให้ $ f: S \ rightarrow \ mathbb {R} $ โดยที่ S ไม่นูนว่างตั้งไว้ใน $ \ mathbb {R} ^ n $ แล้ว $ f \ left (x \ right) $ จะบอกว่านูนบน S ถ้า $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left ( x_2 \ right), \ forall \ lambda \ in \ left (0,1 \ right) $.

ในทางกลับกันให้ $ f: S \ rightarrow \ mathbb {R} $ โดยที่ S ไม่ได้กำหนดนูนว่างไว้ใน $ \ mathbb {R} ^ n $ จากนั้นจะพูด $ f \ left (x \ right) $ จะเว้าบน S ถ้า $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right ) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

ให้ $ f: S \ rightarrow \ mathbb {R} $ โดยที่ S ไม่นูนว่างตั้งไว้ใน $ \ mathbb {R} ^ n $ แล้ว $ f \ left (x \ right) $ จะบอกว่านูนอย่างเคร่งครัดบน S ถ้า $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

ให้ $ f: S \ rightarrow \ mathbb {R} $ โดยที่ S ไม่นูนว่างตั้งไว้ใน $ \ mathbb {R} ^ n $ จากนั้น $ f \ left (x \ right) $ จะถูกกล่าวว่าเว้าอย่างเคร่งครัดบน S ถ้า $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

ตัวอย่าง

• ฟังก์ชันเชิงเส้นมีทั้งแบบนูนและเว้า

• $ f \ left (x \ right) = \ left | x \ right | $ คือฟังก์ชันนูน

• $ f \ left (x \ right) = \ frac {1} {x} $ คือฟังก์ชันนูน

ทฤษฎีบท

ให้ $ f_1, f_2, ... , f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ เป็นฟังก์ชันนูน พิจารณาฟังก์ชัน $ f \ left (x \ right) = \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ alpha_jf_j \ left (x \ right) $ โดยที่ $ \ alpha_j> 0, j = 1, 2, ..k, $ แล้ว $ f \ left (x \ right) $ คือฟังก์ชันนูน

หลักฐาน

ตั้งแต่ $ f_1, f_2, ... f_k $ เป็นฟังก์ชันนูน

ดังนั้น $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $ และ $ i = 1, 2, .... , k $

พิจารณาฟังก์ชัน $ f \ left (x \ right) $

ดังนั้น,

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) $

$ = \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ alpha_jf_j \ left (\ lambda x_1 + 1- \ lambda \ right) x_2 \ leq \ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ alpha_j \ แลมบ์ดา f_j \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_j \ left (x_2 \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ left (\ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ alpha _jf_j \ left ( x_1 \ right) \ right) + \ left (\ displaystyle \ sum \ LIMIT_ {j = 1} ^ k \ alpha _jf_j \ left (x_2 \ right) \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ ซ้าย (x_2 \ right) $

ดังนั้น $ f \ left (x \ right) $ จึงเป็นฟังก์ชันนูน

ทฤษฎีบท

ให้ $ f \ left (x \ right) $ เป็นฟังก์ชันนูนบนชุดนูน $ S \ subset \ mathbb {R} ^ n $ แล้ว minima ท้องถิ่นของ $ f \ left (x \ right) $ บน S คือ a minima ระดับโลก

หลักฐาน

ให้ $ \ hat {x} $ เป็น minima ท้องถิ่นสำหรับ $ f \ left (x \ right) $ และ $ \ hat {x} $ ไม่ใช่ global minima

ดังนั้น $ \ มีอยู่ \ hat {x} \ ใน S $ เช่นนั้น $ f \ left (\ bar {x} \ right) <f \ left (\ hat {x} \ right) $

เนื่องจาก $ \ hat {x} $ เป็น minima ในท้องถิ่นจึงมีย่าน $ N_ \ varepsilon \ left (\ hat {x} \ right) $ ซึ่ง $ f \ left (\ hat {x} \ right) \ leq f \ left (x \ right) \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $

But $f\left ( x \right )$ is a convex function on S, therefore for $\lambda \in \left ( 0, 1 \right )$

we have $\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}\leq \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left ( \bar{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left (\hat{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< f\left (\hat{x} \right ), \forall \lambda \in \left ( 0,1 \right )$

But for some $\lambda<1$ but close to 1, we have

$\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \in N_\varepsilon \left ( \hat{x} \right )\cap S$ and $f\left ( \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \right )< f\left ( \bar{x} \right )$

which is a contradiction.

Hence, $\bar{x}$ is a global minima.

Epigraph

let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ then the epigraph of f denoted by epi(f) or $E_f$ is a subset of $\mathbb{R}^n+1$ defined by $E_f=\left \{ \left ( x,\alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\leq \alpha \right \}$

Hypograph

let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$, then the hypograph of f denoted by hyp(f) or $H_f=\left \{ \left ( x, \alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\geq \alpha \right \}$

Theorem

Let S be a non-empty convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}^n$, then f is convex if and only if its epigraph $E_f$ is a convex set.

Proof

Let f is a convex function.

To show $E_f$ is a convex set.

Let $\left ( x_1, \alpha_1 \right ),\left ( x_2, \alpha_2 \right ) \in E_f,\lambda \in\left ( 0, 1 \right )$

To show $\lambda \left ( x_1,\alpha_1 \right )+\left ( 1-\lambda \right )\left ( x_2, \alpha_2 \right ) \in E_f$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2 \right ]\in E_f$

$f\left ( x_1 \right )\leq \alpha _1, f\left ( x_2\right )\leq \alpha _2$

Therefore, $f\left (\lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f \left ( x_2 \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2$

Converse

Let $E_f$ is a convex set.

To show f is convex.

i.e., to show if $x_1, x_2 \in S,\lambda \left ( 0, 1\right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Let $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right ),f\left ( x_1 \right ), f\left ( x_2 \right ) \in \mathbb{R}$

Since $E_f$ is a convex set, $\left ( \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )\right )f\left ( x_2 \right )\in E_f$

Therefore, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Let S be a non-empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}^n$. Then f is convex if and only if for each integer $k>0$

$x_1,x_2,...x_k \in S, \displaystyle\sum\limits_{i=1}^k \lambda_i=1, \lambda_i\geq 0, \forall i=1,2,s,k$, we have $f\left ( \displaystyle\sum\limits_{i=1}^k \lambda_ix_i \right )\leq \displaystyle\sum\limits_{i=1}^k \lambda _if\left ( x \right )$

Proof

By induction on k.

$k=1:x_1 \in S$ Therefore $f\left ( \lambda_1 x_1\right ) \leq \lambda_i f\left (x_1\right )$ because $\lambda_i=1$.

$k=2:\lambda_1+\lambda_2=1$ and $x_1, x_2 \in S$

Therefore, $\lambda_1x_1+\lambda_2x_2 \in S$

Hence by definition, $f\left ( \lambda_1 x_1 +\lambda_2 x_2 \right )\leq \lambda _1f\left ( x_1 \right )+\lambda _2f\left ( x_2 \right )$

Let the statement is true for $n < k$

Therefore,

$f\left ( \lambda_1 x_1+ \lambda_2 x_2+....+\lambda_k x_k\right )\leq \lambda_1 f\left (x_1 \right )+\lambda_2 f\left (x_2 \right )+...+\lambda_k f\left (x_k \right )$

$k=n+1:$ Let $x_1, x_2,....x_n,x_{n+1} \in S$ and $\displaystyle\sum\limits_{i=1}^{n+1}=1$

Therefore $\mu_1x_1+\mu_2x_2+.......+\mu_nx_n+\mu_{n+1} x_{n+1} \in S$

thus,$f\left (\mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1} x_{n+1} \right )$

$=f\left ( \left ( \mu_1+\mu_2+...+\mu_n \right)\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+\mu_3}+\mu_{n+1}x_{n+1} \right)$

$=f\left ( \mu_y+\mu_{n+1}x_{n+1} \right )$ where $\mu=\mu_1+\mu_2+...+\mu_n$ and

$y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n}$ and also $\mu_1+\mu_{n+1}=1,y \in S$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq \mu f\left ( y \right )+\mu_{n+1} f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq$

$\left ( \mu_1+\mu_2+...+\mu_n \right )f\left ( \frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n} \right )+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n +\mu_{n+1}x_{n+1}\right )\leq \left ( \mu_1+ \mu_2+ ...+\mu_n \right )$

$\left [ \frac{\mu_1}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_1 \right )+...+\frac{\mu_n}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_n \right ) \right ]+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right )\leq \mu_1f\left ( x_1 \right )+\mu_2f\left ( x_2 \right )+....$

Hence Proved.

Let S be a non-empty open set in $\mathbb{R}^n$,then $f:S\rightarrow \mathbb{R}$ is said to be differentiable at $\hat{x} \in S$ if there exist a vector $\bigtriangledown f\left ( \hat{x} \right )$ called gradient vector and a function $\alpha :\mathbb{R}^n\rightarrow \mathbb{R}$ such that

$f\left ( x \right )=f\left ( \hat{x} \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x-\hat{x} \right )+\left \| x=\hat{x} \right \|\alpha \left ( \hat{x}, x-\hat{x} \right ), \forall x \in S$ where

$\alpha \left (\hat{x}, x-\hat{x} \right )\rightarrow 0 \bigtriangledown f\left ( \hat{x} \right )=\left [ \frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n} \right ]_{x=\hat{x}}^{T}$

Theorem

let S be a non-empty, open convexset in $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ be differentiable on S. Then, f is convex if and only if for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f\left ( x_2 \right )$

Proof

Let f be a convex function. i.e., for $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right )$

$f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

$ \Rightarrow f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )+f\left ( x_2 \right )$

$ \Rightarrow\lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2+\lambda \left ( x_1-x_2 \right ) \right )-f\left ( x_2 \right )$

$\Rightarrow \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\lambda +$

$\left \| \lambda \left ( x_1-x_2 \right ) \right \|\alpha \left ( x_2,\lambda\left (x_1 - x_2 \right )-f\left ( x_2 \right ) \right )$

where $\alpha\left ( x_2, \lambda\left (x_1 - x_2 \right ) \right )\rightarrow 0$ as$\lambda \rightarrow 0$

Dividing by $\lambda$ on both sides, we get −

$f\left ( x_1 \right )-f\left ( x_2 \right ) \geq \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right )$

Converse

Let for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f \left ( x_2 \right )$

To show that f is convex.

Since S is convex, $x_3=\lambda x_1+\left (1-\lambda \right )x_2 \in S, \lambda \in \left ( 0, 1 \right )$

Since $x_1, x_3 \in S$, therefore

$f\left ( x_1 \right )-f \left ( x_3 \right ) \geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 -x_3\right )$

$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - \lambda x_1-\left (1-\lambda \right )x_2\right )$

$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \left ( 1- \lambda\right )\bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - x_2\right )$

Since, $x_2, x_3 \in S$ therefore

$f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-\lambda x_1-\left ( 1-\lambda \right )x_2 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \left ( -\lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )$

Thus, combining the above equations, we get −

$\lambda \left ( f\left ( x_1 \right )-f\left ( x_3 \right ) \right )+\left ( 1- \lambda \right )\left ( f\left ( x_2 \right )-f\left ( x_3 \right ) \right )\geq 0$

$\Rightarrow f\left ( x_3\right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Theorem

let S be a non-empty open convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is convex on S if and only if for any $x_1,x_2 \in S,\left ( \bigtriangledown f \left ( x_2 \right )-\bigtriangledown f \left ( x_1 \right ) \right )^T \left ( x_2-x_1 \right ) \geq 0$

Proof

let f be a convex function, then using the previous theorem −

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\leq f\left ( x_1 \right )-f\left ( x_2 \right )$ and

$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

Adding the above two equations, we get −

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_2-x_1 \right )\geq 0$

Converse

Let for any $x_1,x_2 \in S,\left (\bigtriangledown f \left ( x_2\right )- \bigtriangledown f \left ( x_1\right )\right )^T \left ( x_2-x_1\right )\geq 0$

To show that f is convex.

Let $x_1,x_2 \in S$, thus by mean value theorem, $\frac{f\left ( x_1\right )-f\left ( x_2\right )}{x_1-x_2}=\bigtriangledown f\left ( x\right ),x \in \left ( x_1-x_2\right ) \Rightarrow x= \lambda x_1+\left ( 1-\lambda\right )x_2$ because S is a convex set.

$\Rightarrow f\left ( x_1 \right )- f\left ( x_2 \right )=\left ( \bigtriangledown f\left ( x \right )^T \right )\left ( x_1-x_2 \right )$

for $x,x_1$, we know −

$\left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( \lambda x_1+\left ( 1-\lambda \right )x_2-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )- \bigtriangledown f\left ( x_1 \right )\right )^T\left ( 1- \lambda \right )\left ( x_2-x_1 \right )\geq 0$

$\Rightarrow \bigtriangledown f\left ( x \right )^T\left ( x_2-x_1 \right )\geq \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )$

Combining the above equations, we get −

$\Rightarrow \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

Hence using the last theorem, f is a convex function.

Twice Differentiable function

Let S be a non-empty subset of $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ then f is said to be twice differentiable at $\bar{x} \in S$ if there exists a vector $\bigtriangledown f\left (\bar{x}\right ), a \:nXn$ matrix $H\left (x\right )$(called Hessian matrix) and a function $\alpha:\mathbb{R}^n \rightarrow \mathbb{R}$ such that $f\left ( x \right )=f\left ( \bar{x}+x-\bar{x} \right )=f\left ( \bar{x} \right )+\bigtriangledown f\left ( \bar{x} \right )^T\left ( x-\bar{x} \right )+\frac{1}{2}\left ( x-\bar{x} \right )H\left ( \bar{x} \right )\left ( x-\bar{x} \right )$

where $ \alpha \left ( \bar{x}, x-\bar{x} \right )\rightarrow Oasx\rightarrow \bar{x}$

Theorem

Let f be twice differentiable function. If $\bar{x}$ is a local minima, then $\bigtriangledown f\left ( \bar{x} \right )=0$ and the Hessian matrix $H\left ( \bar{x} \right )$ is a positive semidefinite.

Proof

Let $d \in \mathbb{R}^n$. Since f is twice differentiable at $\bar{x}$.

Therefore,

$f\left ( \bar{x} +\lambda d\right )=f\left ( \bar{x} \right )+\lambda \bigtriangledown f\left ( \bar{x} \right )^T d+\lambda^2d^TH\left ( \bar{x} \right )d+\lambda^2d^TH\left ( \bar{x} \right )d+$

$\lambda^2\left \| d \right \|^2\beta \left ( \bar{x}, \lambda d \right )$

But $\bigtriangledown f\left ( \bar{x} \right )=0$ and $\beta\left ( \bar{x}, \lambda d \right )\rightarrow 0$ as $\lambda \rightarrow 0$

$\Rightarrow f\left ( \bar{x} +\lambda d \right )-f\left ( \bar{x} \right )=\lambda ^2d^TH\left ( \bar{x} \right )d$

Since $\bar{x }$ is a local minima, there exists a $\delta > 0$ such that $f\left ( x \right )\leq f\left ( \bar{x}+\lambda d \right ), \forall \lambda \in \left ( 0,\delta \right )$

Theorem

Let $f:S \rightarrow \mathbb{R}^n$ where $S \subset \mathbb{R}^n$ be twice differentiable over S. If $\bigtriangledown f\left ( x\right )=0$ and $H\left ( \bar{x} \right )$ is positive semi-definite, for all $x \in S$, then $\bar{x}$ is a global optimal solution.

Proof

Since $H\left ( \bar{x} \right )$ is positive semi-definite, f is convex function over S. Since f is differentiable and convex at $\bar{x}$

$\bigtriangledown f\left ( \bar{x} \right )^T \left ( x-\bar{x} \right ) \leq f\left (x\right )-f\left (\bar{x}\right ),\forall x \in S$

Since $\bigtriangledown f\left ( \bar{x} \right )=0, f\left ( x \right )\geq f\left ( \bar{x} \right )$

Hence, $\bar{x}$ is a global optima.

Theorem

Suppose $\bar{x} \in S$ is a local optimal solution to the problem $f:S \rightarrow \mathbb{R}$ where S is a non-empty subset of $\mathbb{R}^n$ and S is convex. $min \:f\left ( x \right )$ where $x \in S$.

Then:

• $\bar{x}$ is a global optimal solution.

• If either $\bar{x}$ is strictly local minima or f is strictly convex function, then $\bar{x}$ is the unique global optimal solution and is also strong local minima.

Proof

Let $\bar{x}$ be another global optimal solution to the problem such that $x \neq \bar{x}$ and $f\left ( \bar{x} \right )=f\left ( \hat{x} \right )$

Since $\hat{x},\bar{x} \in S$ and S is convex, then $\frac{\hat{x}+\bar{x}}{2} \in S$ and f is strictly convex.

$\Rightarrow f\left ( \frac{\hat{x}+\bar{x}}{2} \right )< \frac{1}{2} f\left (\bar{x}\right )+\frac{1}{2} f\left (\hat{x}\right )=f\left (\hat{x}\right )$

This is contradiction.

Hence, $\hat{x}$ is a unique global optimal solution.

Corollary

Let $f:S \subset \mathbb{R}^n \rightarrow \mathbb{R}$ be a differentiable convex function where $\phi \neq S\subset \mathbb{R}^n$ is a convex set. Consider the problem $min f\left (x\right ),x \in S$,then $\bar{x}$ is an optimal solution if $\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right ) \geq 0,\forall x \in S.$

Proof

Let $\bar{x}$ is an optimal solution, i.e, $f\left (\bar{x}\right )\leq f\left (x\right ),\forall x \in S$

$\Rightarrow f\left (x\right )=f\left (\bar{x}\right )\geq 0$

$f\left (x\right )=f\left (\bar{x}\right )+\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )+\left \| x-\bar{x} \right \|\alpha \left ( \bar{x},x-\bar{x} \right )$

where $\alpha \left ( \bar{x},x-\bar{x} \right )\rightarrow 0$ as $x \rightarrow \bar{x}$

$\Rightarrow f\left (x\right )-f\left (\bar{x}\right )=\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )\geq 0$

Corollary

Let f be a differentiable convex function at $\bar{x}$,then $\bar{x}$ is global minimum iff $\bigtriangledown f\left (\bar{x}\right )=0$

Examples

• $f\left (x\right )=\left (x^2-1\right )^{3}, x \in \mathbb{R}$.

  $\bigtriangledown f\left (x\right )=0 \Rightarrow x= -1,0,1$.

  $\bigtriangledown^2f\left (\pm 1 \right )=0, \bigtriangledown^2 f\left (0 \right )=6>0$.

  $f\left (\pm 1 \right )=0,f\left (0 \right )=-1$

  Hence, $f\left (x \right ) \geq -1=f\left (0 \right )\Rightarrow f\left (0 \right ) \leq f \left (x \right)\forall x \in \mathbb{R}$

• $f\left (x \right )=x\log x$ defined on $S=\left \{ x \in \mathbb{R}, x> 0 \right \}$.

  ${f}'x=1+\log x$

  ${f}''x=\frac{1}{x}>0$

  Thus, this function is strictly convex.

• $f \left (x \right )=e^{x},x \in \mathbb{R}$ is strictly convex.

Let $f:S \rightarrow \mathbb{R}$ where $S \subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1,x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\lambda \in \left ( 0, 1 \right )$

For example, $f\left ( x \right )=x^{3}$

Let $f:S\rightarrow R $ where $S\subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq min\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}, \lambda \in \left ( 0, 1 \right )$

Remarks

• Every convex function is quasiconvex but the converse is not true.
• A function which is both quasiconvex and quasiconcave is called quasimonotone.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconvex if and only if $S_{\alpha} =\left ( x \in S:f\left ( x \right )\leq \alpha \right \}$ is convex for each real number \alpha$

Proof

Let f is quasiconvex on S.

Let $x_1,x_2 \in S_{\alpha}$ therefore $x_1,x_2 \in S$ and $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$

Let $\lambda \in \left (0, 1 \right )$ and let $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$

Thus, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$

Therefore, $S_{\alpha}$ is convex.

Converse

Let $S_{\alpha}$ is convex for each $\alpha$

$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$

$x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Let $x=\lambda x_1+\left ( 1-\lambda \right )x_2$

For $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$

$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$

$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$

Hence proved.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconcave if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ is convex for each real number $\alpha$.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasimonotone if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ is convex for each real number $\alpha$.

Theorem

Let S be a non empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is quasiconvex if and only if for any $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, we have $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$

Proof

Let f be a quasiconvex function.

Let $x_1,x_2 \in S$ such that $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$

By differentiability of f at $x_2, \lambda \in \left ( 0, 1 \right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$

But since f is quasiconvex, $f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$

But $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ as $\lambda \rightarrow 0$

Therefore, $\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$

Converse

let for $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, $\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$

To show that f is quasiconvex,ie, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$

Proof by contradiction

Suppose there exists an $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ such that $f\left ( x_2 \right )< f \left ( x_3 \right )$ for some $ \lambda \in \left ( 0, 1 \right )$

For $x_2$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$

$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$

For $x_1$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$

$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$

thus, from the above equations, $\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$

Define $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$

Thus we can find $x_0 \in U$ such that $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ for some $\mu _0 \in \left ( 0,1 \right )$ which is nearest to $x_3$ and $\hat{x} \in \left ( x_0,x_1 \right )$ such that by mean value theorem,

$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$

Since $x_0$ is a combination of $x_1$ and $x_2$ and $f\left (x_2 \right )< f\left ( \hat{x}\right )$

By repeating the starting procedure, $\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$

Thus, combining the above equations, we get:

$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$

$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$

Hence, it is contradiction.

Examples

Step 1 − $f\left ( x\right )=X^3$

$Let f \left ( x_1\right )\leq f\left ( x_2\right )$

$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$

$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$

Thus, $f\left ( x\right )$ is quasiconvex.

Step 2 − $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$

Let $\hat{x_1}=\left ( 2, -2\right )$ and $\hat{x_2}=\left ( 1, 0\right )$

thus, $f\left ( \hat{x_1}\right )=0,f\left ( \hat{x_2}\right )=1 \Rightarrow f\left ( \hat{x_1}\right )\setminus < f \left ( \hat{x_2}\right )$

Thus, $\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$

Hence $f\left ( x\right )$ is not quasiconvex.

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is said to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}$

Remarks

• Every strictly quasiconvex function is strictly convex.
• Strictly quasiconvex function does not imply quasiconvexity.
• Strictly quasiconvex function may not be strongly quasiconvex.
• Pseudoconvex function is a strictly quasiconvex function.

Theorem

Let $f:S\rightarrow \mathbb{R}^n$ be strictly quasiconvex function and S be a non-empty convex set in $\mathbb{R}^n$.Consider the problem: $min \:f\left ( x \right ), x \in S$. If $\hat{x}$ is local optimal solution, then $\bar{x}$ is global optimal solution.

Proof

Let there exists $ \bar{x} \in S$ such that $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$

Since $\bar{x},\hat{x} \in S$ and S is convex set, therefore,

$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$

Since $\hat{x}$ is local minima, $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$

Since f is strictly quasiconvex.

$$f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right )< max \left \{ f\left ( \hat{x} \right ),f\left ( \bar{x} \right ) \right \}=f\left ( \hat{x} \right )$$

Hence, it is contradiction.

Strictly quasiconcave function

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$, then f is saud to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left (x_1\right )\neq f\left (x_2\right )$, we have

$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.

Examples

• $f\left (x\right )=x^2-2$

  It is a strictly quasiconvex function because if we take any two points $x_1,x_2$ in the domain that satisfy the constraints in the definition $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )< max \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$ As the function is decreasing in the negative x-axis and it is increasing in the positive x-axis (since it is a parabola).

• $f\left (x\right )=-x^2$

  It is not a strictly quasiconvex function because if we take take $x_1=1$ and $x_2=-1$ and $\lambda=0.5$, then $f\left (x_1\right )=-1=f\left (x_2\right )$ but $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$ Therefore it does not satisfy the conditions stated in the definition. But it is a quasiconcave function because if we take any two points in the domain that satisfy the constraints in the definition $f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$. As the function is increasing in the negative x-axis and it is decreasing in the positive x-axis.

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is strongly quasiconvex function if for any $x_1,x_2 \in S$ with $\left ( x_1 \right ) \neq \left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\forall \lambda \in \left ( 0,1\right )$

Theorem

A quasiconvex function $f:S\rightarrow \mathbb{R}^n$ on a non-empty convex set S in $\mathbb{R}^n$ is strongly quasiconvex function if it is not constant on a line segment joining any points of S.

Proof

Let f is quasiconvex function and it is not constant on a line segment joining any points of S.

Suppose f is not strongly quasiconvex function.

There exist $x_1,x_2 \in S$ with $x_1 \neq x_2$ such that

$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$

$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ and $f\left ( x_2 \right )\leq f\left ( z \right )$

Since f is not constant in $\left [ x_1,z \right ]$ and $\left [z,x_2 \right ] $

So there exists $u \in \left [ x_1,z \right ]$ and $v=\left [ z,x_2 \right ]$

$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$

Since f is quasiconvex,

$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$

$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$

$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$

But z is any point between u and v, if any of them are equal, then f is constant.

Therefore, $max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$

which contradicts the quasiconvexity of f as $z \in \left [ u,v \right ]$.

Hence f is strongly quasiconvex function.

Theorem

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$. If $\hat{x}$ is local optimal solution, then $\hat{x}$ is unique global optimal solution.

Proof

Since a strong quasiconvex function is also strictly quasiconvex function, thus a local optimal solution is global optimal solution.

Uniqueness − Let f attains global optimal solution at two points $u,v \in S$

$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$

If u is global optimal solution, $f\left ( u \right )\leq f\left ( v \right )$ and $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$

$$f\left ( \lambda u+\left ( 1-\lambda\right )v\right )< max \left \{f\left ( u \right ),f\left ( v \right ) \right \}=f\left ( u \right )$$

which is a contradiction.

Hence there exists only one global optimal solution.

Remarks

• A strongly quasiconvex function is also strictly quasiconvex fucntion.
• A strictly convex function may or may not be strongly quasiconvex.
• A differentiable strictly convex is strongly quasiconvex.

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\geq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$

Pseudoconcave function

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1, x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\leq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$

Remarks

• If a function is both pseudoconvex and pseudoconcave, then is is called pseudolinear.

• A differentiable convex function is also pseudoconvex.

• A pseudoconvex function may not be convex. For example,

  $f\left ( x \right )=x+x^3$ is not convex. If $x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$

  Thus,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$

  And, $f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$

  $\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$

  Thus, it is pseudoconvex.

  A pseudoconvex function is strictly quasiconvex. Thus, every local minima of pseudoconvex is also global minima.

Strictly pseudoconvex function

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )> f\left ( x_1 \right )$,or equivalently if $f\left ( x_1 \right )\geq f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$

Theorem

Let f be a pseudoconvex function and suppose $\bigtriangledown f\left ( \hat{x}\right )=0$ for some $\hat{x} \in S$, then $\hat{x}$ is global optimal solution of f over S.

Proof

Let $\hat{x}$ be a critical point of f, ie, $\bigtriangledown f\left ( \hat{x}\right )=0$

Since f is pseudoconvex function, for $x \in S,$ we have

$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$

Hence, $\hat{x}$ is global optimal solution.

Remark

If f is strictly pseudoconvex function, $\hat{x}$ is unique global optimal solution.

Theorem

If f is differentiable pseudoconvex function over S, then f is both strictly quasiconvex as well as quasiconvex function.

Remarks

• The sum of two pseudoconvex fucntions defined on an open set S of $\mathbb{R}^n$ may not be pseudoconvex.

• Let $f:S\rightarrow \mathbb{R}$ be a quasiconvex function and S be a non-empty convex subset of $\mathbb{R}^n$ then f is pseudoconvex if and only if every critical point is a global minima of f over S.

• Let S be a non-empty convex subset of $\mathbb{R}^n$ and $f:S\rightarrow \mathbb{R}$ be a function such that $\bigtriangledown f\left ( x\right )\neq 0$ for every $x \in S$ then f is pseudoconvex if and only if it is a quasiconvex function.

There are four types of convex programming problems −

Step 1 − $min \:f\left ( x \right )$, where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is convex function.

Step 2 − $min \: f\left ( x \right ), x \in \mathbb{R}^n$ subject to

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.

$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.

$g_i\left ( x \right ) = 0, m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.

where $f\left ( x \right )$ is a convex fucntion.

Step 3 − $max \:f\left ( x \right )$ where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is concave function.

Step 4 − $min \:f\left ( x \right )$, where $x \in \mathbb{R}^n$ subject to

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.

$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.

$g_i\left ( x \right ) = 0,m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.

where $f\left ( x \right )$ is a concave function.

Cone of feasible direction

Let S be a non-empty set in $\mathbb{R}^n$ and let $\hat{x} \in \:Closure\left ( S \right )$, then the cone of feasible direction of S at $\hat{x}$, denoted by D, is defined as $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$

Each non-zero vector $d \in D$ is called feasible direction.

For a given function $f:\mathbb{R}^n \Rightarrow \mathbb{R}$ the cone of improving direction at $\hat{x}$ is denoted by F and is given by

$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$

Each direction $d \in F$ is called an improving direction or descent direction of f at $\hat{x}$

Theorem

Necessary Condition

Consider the problem $min f\left ( x \right )$ such that $x \in S$ where S be a non-empty set in $\mathbb{R}^n$. Suppose f is differentiable at a point $\hat{x} \in S$. If $\hat{x}$ is a local optimal solution, then $F_0 \cap D= \phi$ where $F_0=\left \{ d:\bigtriangledown f\left ( \hat{x} \right )^T d < 0 \right \}$ and D is a cone of feasible direction.

Sufficient Condition

If $F_0 \cap D= \phi$ f is a pseudoconvex function at $\hat{x}$ and there exists a neighbourhood of $\hat{x},N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$ such that $d=x-\hat{x}\in D$ for any $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$, then $\hat{x}$ is local optimal solution.

Proof

Necessary Condition

Let $F_0 \cap D\neq \phi$, ie, there exists a $d \in F_0 \cap D$ such that $d \in F_0$ and $d\in D$

Since $d \in D$, therefore there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$

Since $d \in F_0$, therefore $\bigtriangledown f \left ( \hat{x}\right )^T d <0$

Thus, there exists $\delta_2>0$ such that $f\left ( \hat{x}+\lambda d\right )< f\left ( \hat{x}\right ),\forall \lambda \in f \left ( 0,\delta_2 \right )$

Let $\delta=min \left \{\delta_1,\delta_2 \right \}$

Then $\hat{x}+\lambda d \in S, f\left (\hat{x}+\lambda d \right ) < f\left ( \hat{x} \right ),\forall \lambda \in f \left ( 0,\delta \right )$

But $\hat{x}$ is local optimal solution.

Hence it is contradiction.

Thus $F_0\cap D=\phi$

Sufficient Condition

Let $F_0 \cap D\neq \phi$ nd let f be a pseudoconvex function.

Let there exists a neighbourhood of $\hat{x}, N_{\varepsilon}\left ( \hat{x} \right )$ such that $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$

Let $\hat{x}$ is not a local optimal solution.

Thus, there exists $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$ such that $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$

By assumption on $S \cap N_\varepsilon \left ( \hat{x} \right ),d=\left ( \bar{x}-\hat{x} \right )\in D$

By pseudoconvex of f,

$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$

$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$

$\Rightarrow d \in F_0$

hence $F_0\cap D \neq \phi$

which is a contradiction.

Hence, $\hat{x}$ is local optimal solution.

Consider the following problem:$min \:f\left ( x\right )$ where $x \in X$ such that $g_x\left ( x\right ) \leq 0, i=1,2,...,m$

$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ and X is an open set in $\mathbb{R}^n$

Let $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$

Let $\hat{x} \in X$, then $M=\left \{1,2,...,m \right \}$

Let $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$ where I is called index set for all active constraints at $\hat{x}$

Let $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$ where J is called index set for all active constraints at $\hat{x}$.

Let $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$

Let $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$

or $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$

Lemma

If $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ and X is non-empty open set in $\mathbb{R}^n$. Let $\hat{x}\in S$ and $g_i$ are different at $\hat{x}, i \in I$ and let $g_i$ where $i \in J$ are continuous at $\hat{x}$, then $G_0 \subseteq D$.

Proof

Let $d \in G_0$

Since $\hat{x} \in X$ and X is an open set, thus there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in X$ for $\lambda \in \left ( 0, \delta_1\right )$

Also since $g_\hat{x}<0$ and $g_i$ are continuous at $\hat{x}, \forall i \in J$, there exists $\delta_2>0$, $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$

Since $d \in G_0$, therefore, $\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$ thus there exists $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$, for $\lambda \in \left ( 0, \delta_3\right ) i \in J$

Let $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$

therefore, $\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$

$\Rightarrow \hat{x}+\lambda d \in S$

$\Rightarrow d \in D$

$\Rightarrow G_0 \subseteq D$

Hence Proved.

Theorem

Necessary Condition

Let $f$ and $g_i, i \in I$, are different at $\hat{x} \in S,$ and $g_j$ are continous at $\hat{x} \in S$. If $\hat{x}$ is local minima of $S$, then $F_0 \cap G_0=\phi$.

Sufficient Condition

If $F_0 \cap G_0= \phi$ and f is a pseudoconvex function at $\left (\hat{x}, g_i 9x \right ), i \in I$ are strictly pseudoconvex functions over some $\varepsilon$ - neighbourhood of $\hat{x}, \hat{x}$ is a local optimal solution.

หมายเหตุ

• ให้ $ \ hat {x} $ เป็นจุดที่เป็นไปได้เช่น $ \ bigtriangledown f \ left (\ hat {x} \ right) = 0 $ แล้ว $ F_0 = \ phi $ ดังนั้น $ F_0 \ cap G_0 = \ phi $ แต่ $ \ hat {x} $ ไม่ใช่วิธีที่ดีที่สุด

• แต่ถ้า $ \ bigtriangledown g \ left (\ hat {x} \ right) = 0 $ แล้ว $ G_0 = \ phi $ ดังนั้น $ F_0 \ cap G_0 = \ phi $

• พิจารณาปัญหา: ขั้นต่ำ $ f \ left (x \ right) $ เช่นนั้น $ g \ left (x \ right) = 0 $

  ตั้งแต่ $ g \ left (x \ right) = 0 $ ดังนั้น $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ และ $ g_2 \ left (x \ right) = - g \ ซ้าย (x \ right) \ leq 0 $.

  ให้ $ \ hat {x} \ ใน S $ แล้ว $ g_1 \ left (\ hat {x} \ right) = 0 $ และ $ g_2 \ left (\ hat {x} \ right) = 0 $

  แต่ $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = - \ bigtriangledown g_2 \ left (\ hat {x} \ right) $

  ดังนั้น $ G_0 = \ phi $ และ $ F_0 \ cap G_0 = \ phi $

เงื่อนไขที่จำเป็น

ทฤษฎีบท

พิจารณาปัญหา - $ min f \ left (x \ right) $ เช่น $ x \ in X $ โดยที่ X เป็นชุดเปิดใน $ \ mathbb {R} ^ n $ และให้ $ g_i \ left (x \ right) \ leq 0, \ สำหรับ i = 1,2, .... m $.

ให้ $ f: X \ rightarrow \ mathbb {R} $ และ $ g_i: X \ rightarrow \ mathbb {R} $

ให้ $ \ hat {x} $ เป็นทางออกที่เป็นไปได้และปล่อยให้ f และ $ g_i, i \ in I $ แตกต่างกันได้ที่ $ \ hat {x} $ และ $ g_i, i \ in J $ ต่อเนื่องที่ $ \ hat { x} $.

ถ้า $ \ hat {x} $ แก้ปัญหาข้างต้นในเครื่องแสดงว่ามี $ u_0, u_i \ in \ mathbb {R} อยู่ใน I $ เช่นนั้น $ u_0 \ bigtriangledown f \ left (\ hat {x} \ ขวา) + \ displaystyle \ sum \ LIMIT_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) $ = 0

โดยที่ $ u_0, u_i \ geq 0, i \ in I $ และ $ \ left (u_0, u_I \ right) \ neq \ left (0,0 \ right) $

นอกจากนี้หาก $ g_i, i \ in J $ ยังแตกต่างกันได้ที่ $ \ hat {x} $ เงื่อนไขข้างต้นสามารถเขียนเป็น -

$ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ LIMIT_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) $ = 0

$ u_0, u_i \ geq 0, \ forall i = 1,2, .... , m $

$ \ left (u_0, u \ right) \ neq \ left (0,0 \ right), u = \ left (u_1, u_2, s, u_m \ right) \ in \ mathbb {R} ^ m $

หมายเหตุ

• $ u_i $ เรียกว่าตัวคูณ Lagrangian

• เงื่อนไขที่ $ \ hat {x} $ เป็นไปได้กับปัญหาที่กำหนดเรียกว่าเงื่อนไขที่เป็นไปได้เบื้องต้น

• ข้อกำหนด $ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ LIMIT_ {i = 1} ^ m ui \ bigtriangledown g_i \ left (x \ right) = 0 $ เรียกว่า dual feasibility เงื่อนไข.

• เงื่อนไข $ u_ig_i \ left (\ hat {x} \ right) = 0, i = 1, 2, ... m $ เรียกว่าเงื่อนไขความหย่อนยานฟรี เงื่อนไขนี้ต้องใช้ $ u_i = 0, i \ in J $

• เงื่อนไขที่เป็นไปได้เบื้องต้นร่วมกันเงื่อนไขความเป็นไปได้แบบคู่และความหย่อนยานฟรีเรียกว่าเงื่อนไข Fritz-John

เงื่อนไขที่เพียงพอ

ทฤษฎีบท

หากมี $ \ varepsilon $ -neighbourhood ของ $ \ hat {x} N_ \ varepsilon \ left (\ hat {x} \ right), \ varepsilon> 0 $ นั่นแสดงว่า f เป็น pseudoconvex มากกว่า $ N_ \ varepsilon \ left ( \ hat {x} \ right) \ cap S $ และ $ g_i, i \ in I $ เป็น pseudoconvex อย่างเคร่งครัดมากกว่า $ N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $ แล้ว $ \ hat { x} $ เป็นวิธีแก้ปัญหาที่ดีที่สุดในท้องถิ่นสำหรับปัญหาที่อธิบายข้างต้น ถ้า f เป็น pseudoconvex ที่ $ \ hat {x} $ และถ้า $ g_i i \ in I $ มีทั้งฟังก์ชัน pseudoconvex และ quasiconvex อย่างเคร่งครัดที่ $ \ hat {x} \ hat {x} $ เป็นวิธีแก้ปัญหาที่ดีที่สุดระดับโลก อธิบายไว้ข้างต้น.

ตัวอย่าง

• $ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

  เช่นนั้น $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5, x_1 + 2x_2 \ leq 4, x_1, x_2 \ geq 0 $ และ $ \ hat {x} = \ left (2 , 1 \ right) $

  ให้ $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5, $

  $ g_2 \ left (x_1, x_2 \ right) = x_1 + 2x_2-4, $

  $ g_3 \ left (x_1, x_2 \ right) = - x_1 $ และ $ g_4 \ left (x_1, x_2 \ right) = -x_2 $

  ดังนั้นข้อ จำกัด ข้างต้นสามารถเขียนเป็น -

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_3 \ left (x_1, x_2 \ right) \ leq 0 $ และ

  $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ ดังนั้น $ I = \ left \ {1,2 \ right \} $ ดังนั้น $ u_3 = 0, u_4 = 0 $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right ) $ และ $ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

  ดังนั้นเราจึงได้รับค่าเหล่านี้ในเงื่อนไขแรกของเงื่อนไข Fritz-John

  $ u_0 = \ frac {3} {2} u_2, \: \: u_1 = \ frac {1} {2} u_2, $ และให้ $ u_2 = 1 $ ดังนั้น $ u_0 = \ frac {3} {2} , \: \: u_1 = \ frac {1} {2} $

  ดังนั้นเงื่อนไขของ Fritz John จึงพอใจ

• $ min f \ left (x_1, x_2 \ right) = - x_1 $.

  เช่นนั้น $ x_2- \ left (1-x_1 \ right) ^ 3 \ leq 0 $,

  $ -x_2 \ leq 0 $ และ $ \ hat {x} = \ left (1,0 \ right) $

  ให้ $ g_1 \ left (x_1, x_2 \ right) = x_2- \ left (1-x_1 \ right) ^ 3 $,

  $ g_2 \ left (x_1, x_2 \ right) = - x_2 $

  ดังนั้นข้อ จำกัด ข้างต้นจึงสามารถปรับเปลี่ยนเป็น -

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  ดังนั้น $ I = \ left \ {1,2 \ right \} $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (-1,0 \ right) $

  $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (0,1 \ right) $ และ $ g_2 \ left (\ hat {x} \ right) = \ left (0, -1 \ right ) $

  ดังนั้นเราจึงได้รับค่าเหล่านี้ในเงื่อนไขแรกของเงื่อนไข Fritz-John

  $ u_0 = 0, \: \: u_1 = u_2 = a> 0 $

  ดังนั้นเงื่อนไขของ Fritz John จึงพอใจ

พิจารณาปัญหา -

$ min \: f \ left (x \ right) $ เช่นนั้น $ x \ ใน X $ โดยที่ X เป็นชุดเปิดใน $ \ mathbb {R} ^ n $ และ $ g_i \ left (x \ right) \ leq 0, ผม = 1, 2, ... , m $

ให้ $ S = \ left \ {x \ in X: g_i \ left (x \ right) \ leq 0, \ forall i \ right \} $

ให้ $ \ hat {x} \ ใน S $ และให้ $ f $ และ $ g_i, i \ in I $ แตกต่างกันได้ที่ $ \ hat {x} $ และ $ g_i, i \ in J $ ต่อเนื่องที่ $ \ hat {x} $. นอกจากนี้ $ \ bigtriangledown g_i \ left (\ hat {x} \ right) i \ in I $ เป็นอิสระเชิงเส้น หาก $ \ hat {x} $ แก้ปัญหาข้างต้นในเครื่องแสดงว่ามี $ u_i อยู่ใน I $ เช่นนั้น

$ \ bigtriangledown f \ left (x \ right) + \ displaystyle \ sum \ LIMIT_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $, $ \: \: u_i \ geq 0, i \ in I $

ถ้า $ g_i i \ in J $ ก็แตกต่างกันได้ที่ $ \ hat {x} $ แล้ว $ \ hat {x} $ แล้ว

$ \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ LIMIT_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) = 0, \ forall i = 1,2, ... , m $

$ u_i \ geq 0 \ สำหรับ i = 1,2, ... , m $

ตัวอย่าง

พิจารณาปัญหาต่อไปนี้ -

$ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

เช่นนั้น $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5 $,

$ x_1,2x_2 \ geq 0 $ และ $ \ hat {x} = \ left (2,1 \ right) $

ให้ $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5 $,

$ g_2 \ left (x_1, x_2 \ right) = x_ {1} + 2x_2-4 $

$ g_3 \ left (x_1, x_2 \ right) = - x_ {1} $ และ $ g_4 \ left (x_1, x_2 \ right) = - x_2 $

ดังนั้นข้อ จำกัด ข้างต้นสามารถเขียนเป็น -

$ g_1 \ left (x_1, x_2 \ right) \ leq 0, g_2 \ left (x_1, x_2 \ right) \ leq 0 $

$ g_3 \ left (x_1, x_2 \ right) \ leq 0, $ และ $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ ดังนั้น $ I = \ left \ {1,2 \ right \} $ ดังนั้น , $ u_3 = 0, \: \: u_4 = 0 $

$ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right ) $ และ

$ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

ดังนั้นเราจึงได้รับค่าเหล่านี้ในเงื่อนไขแรกของเงื่อนไข Karush-Kuhn-Tucker -

$ u_1 = \ frac {1} {3} $ และ $ u_2 = \ frac {2} {3} $

ดังนั้นเงื่อนไข Karush-Kuhn-Tucker จึงเป็นที่พอใจ

วิธีการโคตรชัน

วิธีนี้เรียกอีกอย่างว่าวิธีการไล่ระดับสีหรือวิธีของ Cauchy วิธีนี้เกี่ยวข้องกับคำศัพท์ต่อไปนี้ -

$$ x_ {k + 1} = x_k + \ alpha_kd_k $$

$ d_k = - \ bigtriangledown f \ left (x_k \ right) $ หรือ $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $

ให้ $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $

โดยการแยกความแตกต่างของ $ \ phi $ และเทียบกับศูนย์เราจะได้ $ \ alpha $

ดังนั้นอัลกอริทึมจะเป็นดังนี้ -

• เริ่มต้น $ x_0 $, $ \ varepsilon_1 $, $ \ varepsilon_2 $ และตั้งค่า $ k = 0 $

• ตั้งค่า $ d_k = - \ bigtriangledown f \ left (x_k \ right) $ หรือ $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $.

• หา $ \ alpha_k $ เพื่อที่จะย่อ $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $

• ตั้งค่า $ x_ {k + 1} = x_k + \ alpha_kd_k $

• ถ้า $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $ หรือ $ \ left \ | \ bigtriangledown f \ left (x_ {k + 1} \ right) \ right \ | \ leq \ varepsilon_2 $ ไปที่ขั้นตอนที่ 6 หรือตั้งค่า $ k = k + 1 $ แล้วไปที่ขั้นตอนที่ 2

• ทางออกที่ดีที่สุดคือ $ \ hat {x} = x_ {k + 1} $

วิธีนิวตัน

Newton Method ทำงานบนหลักการต่อไปนี้ -

$ f \ left (x \ right) = y \ left (x \ right) = f \ left (x_k \ right) + \ left (x-x_k \ right) ^ T \ bigtriangledown f \ left (x_k \ right) + \ frac {1} {2} \ left (x-x_k \ right) ^ TH \ left (x_k \ right) \ left (x-x_k \ right) $

$ \ bigtriangledown y \ left (x \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x-x_k \ right) $

ที่ $ x_ {k + 1} \ bigtriangledown y \ left (x_ {k + 1} \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x_ {k +1} -x_k \ right) $

เพื่อให้ $ x_ {k + 1} $ เป็นทางออกที่ดีที่สุด $ \ bigtriangledown y \ left (x_k + 1 \ right) = 0 $

ดังนั้น $ x_ {k + 1} = x_k-H \ left (x_k \ right) ^ {- 1} \ bigtriangledown f \ left (x_k \ right) $

ที่นี่ $ H \ left (x_k \ right) $ ควรไม่ใช่เอกพจน์

ดังนั้นอัลกอริทึมจึงเป็นดังนี้ -

Step 1 - เริ่มต้น $ x_0, \ varepsilon $ และตั้งค่า $ k = 0 $

Step 2 - หา $ H \ left (x_k \ right) \ bigtriangledown f \ left (x_k \ right) $

Step 3 - แก้ระบบเชิงเส้น $ H \ left (x_k \ right) h \ left (x_k \ right) = \ bigtriangledown f \ left (x_k \ right) $ สำหรับ $ h \ left (x_k \ right) $

Step 4 - หา $ x_ {k + 1} = x_k-h \ left (x_k \ right) $

Step 5- ถ้า $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ หรือ $ \ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ | \ leq \ varepsilon $ จากนั้นไปที่ขั้นตอนที่ 6 แล้วตั้งค่า $ k = k + 1 $ แล้วไปที่ขั้นตอนที่ 2

Step 6 - ทางออกที่ดีที่สุดคือ $ \ hat {x} = x_ {k + 1} $

ผันวิธีการไล่ระดับสี

วิธีนี้ใช้สำหรับการแก้ปัญหาประเภทต่อไปนี้ -

$ min f \ left (x \ right) = \ frac {1} {2} x ^ T Qx-bx $

โดยที่ Q คือเมทริกซ์ nXn ที่แน่นอนเป็นบวกและ b เป็นค่าคงที่

ให้ $ x_0, \ varepsilon, $ compute $ g_0 = Qx_0-b $

ตั้ง $ d_0 = -g_0 $ สำหรับ $ k = 0,1,2, ... , $

ตั้งค่า $ \ alpha_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Q d_k} $

คำนวณ $ x_ {k + 1} = x_k + \ alpha_kd_k $

ตั้งค่า $ g_ {k + 1} = g_k + \ alpha_kd_k $

คำนวณ $ \ beta_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Qd_k} $

คำนวณ $ x_ {k + 1} = x_k + \ alpha_kd_k $

ตั้งค่า $ g_ {k + 1} = x_k + \ alpha_kQd_k $

คำนวณ $ \ beta_k = \ frac {g_ {k + 1} ^ {T} g_ {k + 1}} {g_ {k} ^ {T} gk} $

ตั้งค่า $ d_ {k + 1} = - g_ {k + 1} + \ beta_kd_k $