คณิตศาสตร์ไม่ต่อเนื่อง - คู่มือฉบับย่อ
คณิตศาสตร์สามารถแบ่งออกเป็นสองประเภทอย่างกว้าง ๆ -
Continuous Mathematics- มันขึ้นอยู่กับเส้นจำนวนต่อเนื่องหรือจำนวนจริง มีลักษณะเฉพาะด้วยความจริงที่ว่าระหว่างสองจำนวนใด ๆ มักจะมีชุดตัวเลขที่ไม่มีที่สิ้นสุด ตัวอย่างเช่นฟังก์ชันในคณิตศาสตร์ต่อเนื่องสามารถพล็อตเป็นเส้นโค้งเรียบโดยไม่หยุดพัก
Discrete Mathematics- เกี่ยวข้องกับค่าที่แตกต่างกัน นั่นคือระหว่างสองจุดใด ๆ จะมีจำนวนคะแนนที่นับได้ ตัวอย่างเช่นหากเรามีชุดของวัตถุที่ จำกัด ฟังก์ชันสามารถกำหนดเป็นรายการคู่ลำดับที่มีวัตถุเหล่านี้และสามารถนำเสนอเป็นรายการคู่ทั้งหมดได้
หัวข้อในคณิตศาสตร์ไม่ต่อเนื่อง
แม้ว่าจะไม่มีจำนวนสาขาที่แน่นอนของคณิตศาสตร์ไม่ต่อเนื่อง แต่หัวข้อต่อไปนี้มักจะกล่าวถึงในการศึกษาเกี่ยวกับเรื่องนี้ -
- ชุดความสัมพันธ์และฟังก์ชั่น
- ตรรกะทางคณิตศาสตร์
- ทฤษฎีกลุ่ม
- ทฤษฎีการนับ
- Probability
- การเหนี่ยวนำทางคณิตศาสตร์และความสัมพันธ์การเกิดซ้ำ
- ทฤษฎีกราฟ
- Trees
- พีชคณิตบูลีน
เราจะพูดถึงแต่ละแนวคิดเหล่านี้ในบทต่อ ๆ ไปของบทช่วยสอนนี้
นักคณิตศาสตร์ชาวเยอรมัน G. Cantorแนะนำแนวคิดของชุด เขาได้กำหนดชุดเป็นชุดของวัตถุที่ชัดเจนและแยกแยะได้ซึ่งเลือกโดยกฎหรือคำอธิบายบางอย่าง
Setทฤษฎีเป็นพื้นฐานของการศึกษาสาขาอื่น ๆ เช่นทฤษฎีการนับความสัมพันธ์ทฤษฎีกราฟและเครื่องกำหนดสถานะ จำกัด ในบทนี้เราจะกล่าวถึงแง่มุมต่างๆSet Theory.
ชุด - คำจำกัดความ
ชุดคือชุดขององค์ประกอบต่างๆที่ไม่เรียงลำดับ ชุดสามารถเขียนอย่างชัดเจนโดยการระบุองค์ประกอบโดยใช้วงเล็บชุด หากลำดับขององค์ประกอบมีการเปลี่ยนแปลงหรือองค์ประกอบใด ๆ ของชุดซ้ำจะไม่ทำการเปลี่ยนแปลงใด ๆ ในชุด
ตัวอย่างบางส่วนของชุด
- ชุดของจำนวนเต็มบวกทั้งหมด
- ชุดของดาวเคราะห์ทั้งหมดในระบบสุริยะ
- ชุดของรัฐทั้งหมดในอินเดีย
- ชุดตัวอักษรพิมพ์เล็กทั้งหมดของตัวอักษร
การเป็นตัวแทนของชุด
ชุดสามารถแสดงได้สองวิธี -
- บัญชีรายชื่อหรือรูปแบบตาราง
- ตั้งค่าสัญกรณ์ตัวสร้าง
บัญชีรายชื่อหรือรูปแบบตาราง
ชุดนี้แสดงโดยการแสดงรายการองค์ประกอบทั้งหมดที่ประกอบด้วยชุดนั้น องค์ประกอบอยู่ภายในวงเล็บปีกกาและคั่นด้วยเครื่องหมายจุลภาค
Example 1 - ชุดสระในตัวอักษรภาษาอังกฤษ $A = \lbrace a,e,i,o,u \rbrace$
Example 2 - ชุดเลขคี่น้อยกว่า 10 $B = \lbrace 1,3,5,7,9 \rbrace$
ตั้งค่าสัญกรณ์ตัวสร้าง
ชุดถูกกำหนดโดยการระบุคุณสมบัติที่องค์ประกอบของชุดมีเหมือนกัน ชุดนี้อธิบายว่า$A = \lbrace x : p(x) \rbrace$
Example 1 - ชุด $\lbrace a,e,i,o,u \rbrace$ เขียนเป็น -
$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$
Example 2 - ชุด $\lbrace 1,3,5,7,9 \rbrace$ เขียนเป็น -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
หากองค์ประกอบ x เป็นสมาชิกของเซต S ใด ๆ องค์ประกอบนั้นจะแสดงด้วย $x \in S$ และถ้าองค์ประกอบ y ไม่ใช่สมาชิกของเซต S องค์ประกอบนั้นจะแสดงด้วย $y \notin S$.
Example- ถ้า$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ แต่ $1.5 \notin S$
ชุดที่สำคัญบางอย่าง
N - ชุดของตัวเลขธรรมชาติทั้งหมด = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - เซตของจำนวนเต็มทั้งหมด = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - เซตของจำนวนเต็มบวกทั้งหมด
Q - ชุดของตัวเลขที่มีเหตุผลทั้งหมด
R - ชุดของจำนวนจริงทั้งหมด
W - ชุดของจำนวนเต็มทั้งหมด
Cardinality ของชุด
Cardinality ของเซต S แสดงโดย $|S|$คือจำนวนองค์ประกอบของชุด หมายเลขนี้เรียกอีกอย่างว่าหมายเลขคาร์ดินัล หากชุดมีองค์ประกอบจำนวนไม่ จำกัด จำนวนองค์ประกอบจะเท่ากับ$\infty$.
Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
หากมีสองชุด X และ Y
$|X| = |Y|$หมายถึงชุด X และ Y สองชุดที่มีความสำคัญเท่ากัน เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X เท่ากับจำนวนองค์ประกอบใน Y ในกรณีนี้มีฟังก์ชัน bijective 'f' จาก X ถึง Y
$|X| \le |Y|$หมายถึงว่าเซตคาร์ดินาลลิตี้ของ X น้อยกว่าหรือเท่ากับเซตคาร์ดินาลลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่าหรือเท่ากับ Y ที่นี่มีฟังก์ชันฉีด 'f' จาก X ถึง Y
$|X| \lt |Y|$หมายถึงว่าคาร์ดินาลลิตี้ของเซต X น้อยกว่าเซ็ตคาร์ดินาลลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่า Y ในที่นี้ฟังก์ชัน 'f' จาก X ถึง Y เป็นฟังก์ชันแบบฉีด แต่ไม่ได้เป็น bijective
$If\ |X| \le |Y|$ และ $|X| \ge |Y|$ แล้ว $|X| = |Y|$. ชุด X และ Y มักเรียกกันว่าเซตที่เท่ากัน
ประเภทของชุด
ชุดสามารถแบ่งออกเป็นหลายประเภท บางส่วนเป็นแบบ จำกัด ไม่สิ้นสุดเซตย่อยสากลเหมาะสมชุดซิงเกิลตัน ฯลฯ
ชุดไฟไนต์
ชุดที่มีจำนวนองค์ประกอบที่แน่นอนเรียกว่าเซต จำกัด
Example - $S = \lbrace x \:| \:x \in N$ และ $70 \gt x \gt 50 \rbrace$
ชุดไม่มีที่สิ้นสุด
ชุดที่มีองค์ประกอบจำนวนไม่ จำกัด เรียกว่าเซตไม่มีที่สิ้นสุด
Example - $S = \lbrace x \: | \: x \in N $ และ $ x \gt 10 \rbrace$
ชุดย่อย
เซต X คือเซตย่อยของเซต Y (เขียนเป็น $X \subseteq Y$) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y
Example 1 - ให้ $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ และ $Y = \lbrace 1, 2 \rbrace$. เซต Y เป็นเซตย่อยของเซต X เนื่องจากองค์ประกอบทั้งหมดของเซต Y อยู่ในเซต X ดังนั้นเราสามารถเขียน$Y \subseteq X$.
Example 2 - ให้ $X = \lbrace 1, 2, 3 \rbrace$ และ $Y = \lbrace 1, 2, 3 \rbrace$. เซต Y เป็นเซตย่อย (ไม่ใช่เซตย่อยที่เหมาะสม) ของเซต X เนื่องจากองค์ประกอบทั้งหมดของเซต Y อยู่ในเซต X ดังนั้นเราสามารถเขียน$Y \subseteq X$.
ชุดย่อยที่เหมาะสม
คำว่า "ชุดย่อยที่เหมาะสม" สามารถกำหนดเป็น "ชุดย่อย แต่ไม่เท่ากับ" เซต X เป็นเซตย่อยที่เหมาะสมของเซต Y (เขียนเป็น$ X \subset Y $) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y และ $|X| \lt |Y|$.
Example - ให้ $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ และ $Y = \lbrace 1, 2 \rbrace$. ที่นี่ตั้ง$Y \subset X$ ตั้งแต่องค์ประกอบทั้งหมดใน $Y$ มีอยู่ใน $X$ ด้วยและ $X$ มีอย่างน้อยหนึ่งองค์ประกอบมากกว่าที่ตั้งไว้ $Y$.
ชุดสากล
เป็นการรวบรวมองค์ประกอบทั้งหมดในบริบทหรือแอปพลิเคชันเฉพาะ ชุดทั้งหมดในบริบทหรือแอปพลิเคชันนั้นเป็นส่วนย่อยของชุดสากลนี้ ชุดสากลแสดงเป็น$U$.
Example - เราอาจกำหนด $U$เป็นชุดของสัตว์ทุกชนิดบนโลก ในกรณีนี้ชุดของสัตว์เลี้ยงลูกด้วยนมทั้งหมดเป็นชุดย่อยของ$U$ชุดของปลาทั้งหมดเป็นชุดย่อยของ $U$ชุดของแมลงทั้งหมดเป็นส่วนย่อยของ $U$และอื่น ๆ
Set Empty หรือ Null Set
ชุดว่างไม่มีองค์ประกอบ แสดงโดย$\emptyset$. เนื่องจากจำนวนองค์ประกอบในเซตว่างมีจำนวน จำกัด เซตว่างจึงเป็นเซต จำกัด จำนวนเต็มของเซตว่างหรือเซตว่างเป็นศูนย์
Example - $S = \lbrace x \:| \: x \in N$ และ $7 \lt x \lt 8 \rbrace = \emptyset$
Singleton Set หรือ Unit Set
ชุด Singleton หรือชุดหน่วยประกอบด้วยองค์ประกอบเดียว ชุดซิงเกิลตันแสดงโดย$\lbrace s \rbrace$.
Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
ชุดที่เท่ากัน
ถ้าสองชุดมีองค์ประกอบเดียวกันก็จะถือว่าเท่ากัน
Example - ถ้า $A = \lbrace 1, 2, 6 \rbrace$ และ $B = \lbrace 6, 1, 2 \rbrace$พวกมันมีค่าเท่ากันทุกองค์ประกอบของเซต A คือองค์ประกอบของเซต B และทุกองค์ประกอบของเซต B คือองค์ประกอบของเซต A
ชุดที่เทียบเท่า
หากความสำคัญของสองชุดเหมือนกันจะเรียกว่าชุดที่เท่ากัน
Example - ถ้า $A = \lbrace 1, 2, 6 \rbrace$ และ $B = \lbrace 16, 17, 22 \rbrace$พวกมันเทียบเท่ากับคาร์ดินาลลิตี้ของ A เท่ากับคาร์ดินาลลิตี้ของบีคือ $|A| = |B| = 3$
ชุดที่ทับซ้อนกัน
สองชุดที่มีองค์ประกอบร่วมอย่างน้อยหนึ่งชุดเรียกว่าชุดที่ทับซ้อนกัน
กรณีชุดทับ -
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
Example - ให้ $A = \lbrace 1, 2, 6 \rbrace$ และ $B = \lbrace 6, 12, 42 \rbrace$. มีองค์ประกอบทั่วไป '6' ดังนั้นชุดเหล่านี้จึงเป็นชุดที่ทับซ้อนกัน
ชุดไม่ปะติดปะต่อ
ชุด A และ B สองชุดเรียกว่าชุดไม่ปะติดปะต่อกันหากไม่มีองค์ประกอบที่เหมือนกันแม้แต่ชิ้นเดียว ดังนั้นชุดที่ไม่ปะติดปะต่อจึงมีคุณสมบัติดังต่อไปนี้ -
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
Example - ให้ $A = \lbrace 1, 2, 6 \rbrace$ และ $B = \lbrace 7, 9, 14 \rbrace$ไม่มีองค์ประกอบร่วมกันดังนั้นชุดเหล่านี้จึงเป็นชุดที่ทับซ้อนกัน
เวนน์ไดอะแกรม
แผนภาพเวนน์ประดิษฐ์ขึ้นในปี พ.ศ. 2423 โดยจอห์นเวนน์เป็นแผนภาพที่แสดงความสัมพันธ์เชิงตรรกะที่เป็นไปได้ทั้งหมดระหว่างชุดทางคณิตศาสตร์ที่แตกต่างกัน
Examples
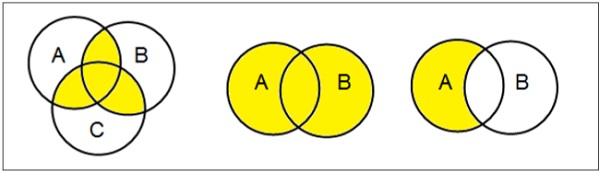
ตั้งค่าการทำงาน
การดำเนินการชุดประกอบด้วย Set Union, Set Intersection, Set Difference, Complement of Set และ Cartesian Product
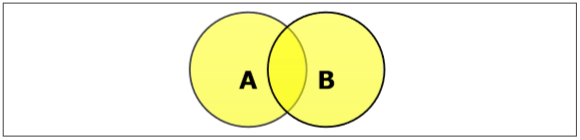
ตั้งสหภาพ
การรวมกันของเซต A และ B (แสดงโดย $A \cup B$) คือชุดขององค์ประกอบที่อยู่ใน A ใน B หรือทั้ง A และ B ดังนั้น $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.
Example - ถ้า $A = \lbrace 10, 11, 12, 13 \rbrace$ และ B = $\lbrace 13, 14, 15 \rbrace$แล้ว $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (องค์ประกอบร่วมเกิดขึ้นเพียงครั้งเดียว)
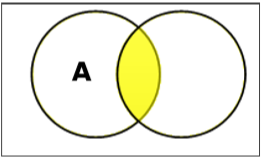
ตั้งค่าทางแยก
จุดตัดของเซต A และ B (แสดงโดย $A \cap B$) คือชุดขององค์ประกอบที่อยู่ในทั้ง A และ B ดังนั้น $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.
Example - ถ้า $A = \lbrace 11, 12, 13 \rbrace$ และ $B = \lbrace 13, 14, 15 \rbrace$แล้ว $A \cap B = \lbrace 13 \rbrace$.
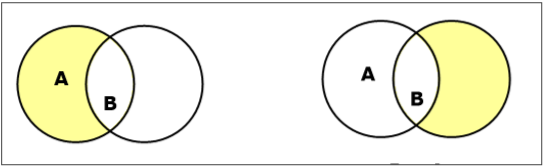
ตั้งค่าความแตกต่าง / ส่วนเสริมสัมพัทธ์
ความแตกต่างของเซต A และ B (แสดงโดย $A – B$) คือชุดขององค์ประกอบที่อยู่ใน A เท่านั้น แต่ไม่ใช่ใน B ดังนั้น $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.
Example - ถ้า $A = \lbrace 10, 11, 12, 13 \rbrace$ และ $B = \lbrace 13, 14, 15 \rbrace$แล้ว $(A - B) = \lbrace 10, 11, 12 \rbrace$ และ $(B - A) = \lbrace 14, 15 \rbrace$. ที่นี่เราสามารถเห็น$(A - B) \ne (B - A)$
การเสริมชุด
ส่วนประกอบของชุด A (แสดงโดย $A’$) คือชุดขององค์ประกอบที่ไม่ได้อยู่ในชุด A ดังนั้น $A' = \lbrace x | x \notin A \rbrace$.
โดยเฉพาะอย่างยิ่ง, $A'= (U - A)$ ที่ไหน $U$ เป็นชุดสากลที่มีวัตถุทั้งหมด
Example - ถ้า $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ แล้ว $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$

ผลิตภัณฑ์คาร์ทีเซียน / ผลิตภัณฑ์ข้าม
ผลคูณคาร์ทีเซียนของ n จำนวนชุด $A_1, A_2, \dots A_n$ แสดงเป็น $A_1 \times A_2 \dots \times A_n$ สามารถกำหนดเป็นคู่คำสั่งที่เป็นไปได้ทั้งหมด $(x_1, x_2, \dots x_n)$ ที่ไหน $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
Example - ถ้าเราใช้สองชุด $A = \lbrace a, b \rbrace$ และ $B = \lbrace 1, 2 \rbrace$,
ผลคูณคาร์ทีเซียนของ A และ B เขียนเป็น - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
ผลคูณคาร์ทีเซียนของ B และ A เขียนเป็น - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
ชุดไฟ
เซตกำลังของเซต S คือเซตของเซตย่อยทั้งหมดของ S รวมเซตว่าง คาร์ดินาลิตี้ของเซตกำลังของเซต S ของคาร์ดินาลิตี้ n คือ$2^n$. ชุดไฟแสดงเป็น$P(S)$.
Example −
สำหรับชุด $S = \lbrace a, b, c, d \rbrace$ ให้เราคำนวณส่วนย่อย -
ชุดย่อยที่มี 0 องค์ประกอบ - $\lbrace \emptyset \rbrace$ (ชุดว่าง)
Subsets ที่มี 1 องค์ประกอบ - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
ย่อยที่มี 2 องค์ประกอบ - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
ย่อยที่มี 3 องค์ประกอบ - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
ย่อยที่มี 4 องค์ประกอบ - $\lbrace a, b, c, d \rbrace$
ดังนั้น $P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
Note - ชุดไฟของชุดว่างก็เป็นชุดเปล่าเช่นกัน
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
การแบ่งส่วนของชุด
พาร์ติชันของชุดพูดSเป็นคอลเลกชันของnย่อยเคลื่อนพูด$P_1, P_2, \dots P_n$ ที่เป็นไปตามเงื่อนไขสามประการต่อไปนี้ -
$P_i$ ไม่มีชุดว่าง
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
การรวมกันของส่วนย่อยต้องเท่ากับชุดเดิมทั้งหมด
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
จุดตัดของชุดที่แตกต่างกันสองชุดว่างเปล่า
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$
Example
ปล่อย $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
การแบ่งพาร์ติชันที่เป็นไปได้อย่างหนึ่งคือ $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
การแบ่งพาร์ติชันที่เป็นไปได้อีกประการหนึ่งคือ $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
เบลล์เบอร์
หมายเลขกระดิ่งให้การนับจำนวนวิธีในการแบ่งชุด พวกเขาแสดงโดย$B_n$ โดยที่ n คือจำนวนสมาชิกของเซต
Example -
ปล่อย $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
พาร์ติชันอื่นคือ -
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
ดังนั้น $B_3 = 5$
เมื่อใดก็ตามที่มีการหารือเกี่ยวกับเซตความสัมพันธ์ระหว่างองค์ประกอบของเซตคือสิ่งต่อไปที่เกิดขึ้น Relations อาจมีอยู่ระหว่างวัตถุในชุดเดียวกันหรือระหว่างวัตถุสองชุดขึ้นไป
ความหมายและคุณสมบัติ
ความสัมพันธ์ไบนารี R จากเซต x ถึง y (เขียนเป็น $xRy$ หรือ $R(x,y)$) เป็นส่วนย่อยของผลิตภัณฑ์คาร์ทีเซียน $x \times y$. หากคู่ที่สั่งซื้อของ G กลับรายการความสัมพันธ์ก็จะเปลี่ยนไปเช่นกัน
โดยทั่วไปแล้วความสัมพันธ์ n-ary R ระหว่างเซต $A_1, \dots ,\ and\ A_n$ เป็นส่วนย่อยของผลิตภัณฑ์ n-ary $A_1 \times \dots \times A_n$. คาร์ดินาลลิตี้ต่ำสุดของความสัมพันธ์ R คือศูนย์และสูงสุดคือ$n^2$ ในกรณีนี้.
ความสัมพันธ์ไบนารี R บนชุดเดียว A เป็นส่วนย่อยของ $A \times A$.
สำหรับสองชุดที่แตกต่างกัน A และ B มี cardinalities mและnตามลำดับ cardinality สูงสุดของความสัมพันธ์ R จาก A ถึง B เป็นล้าน
โดเมนและช่วง
หากมีสองชุด A และ B และความสัมพันธ์ R มีคู่คำสั่ง (x, y) แล้ว -
domain ของ R, Dom (R) คือเซต $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
range ของ R, Ran (R) คือชุด $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
ตัวอย่าง
ปล่อย, $A = \lbrace 1, 2, 9 \rbrace $ และ $ B = \lbrace 1, 3, 7 \rbrace$
กรณีที่ 1 - ถ้าความสัมพันธ์ R เท่ากับ 'เท่ากับ' แล้ว $R = \lbrace (1, 1), (3, 3) \rbrace$
ดอม (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
กรณีที่ 2 - ถ้าความสัมพันธ์ R เป็น 'น้อยกว่า' แล้ว $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
ดอม (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
กรณีที่ 3 - ถ้าความสัมพันธ์ R เป็น 'มากกว่า' แล้ว $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
ดอม (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
การแสดงความสัมพันธ์โดยใช้กราฟ
ความสัมพันธ์สามารถแสดงโดยใช้กราฟกำกับ
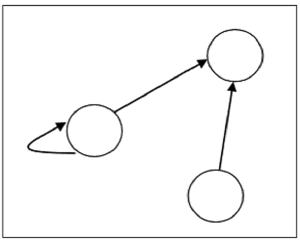
จำนวนจุดยอดในกราฟเท่ากับจำนวนองค์ประกอบในชุดที่กำหนดความสัมพันธ์ สำหรับแต่ละคู่ที่เรียงลำดับ (x, y) ในความสัมพันธ์ R จะมีขอบกำกับจากจุดยอด 'x' ถึงจุดยอด 'y' หากมีคู่ลำดับ (x, x) จะมีการวนรอบตัวเองที่จุดยอด 'x'
สมมติว่ามีความสัมพันธ์ $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ ในชุด $S = \lbrace 1, 2, 3 \rbrace$สามารถแสดงได้ด้วยกราฟต่อไปนี้ -
ประเภทของความสัมพันธ์
Empty Relation ระหว่างเซต X และ Y หรือบน E คือเซตว่าง $\emptyset$
Full Relation ระหว่างเซต X และ Y คือเซต $X \times Y$
Identity Relation ในเซต X คือเซต $\lbrace (x, x) | x \in X \rbrace$
ความสัมพันธ์ผกผัน R 'ของความสัมพันธ์ R ถูกกำหนดเป็น - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example - ถ้า $R = \lbrace (1, 2), (2, 3) \rbrace$ แล้ว $R' $ จะ $\lbrace (2, 1), (3, 2) \rbrace$
เรียกความสัมพันธ์ R บนเซต A Reflexive ถ้า $\forall a \in A$ เกี่ยวข้องกับ (aRa hold)
Example - ความสัมพันธ์ $R = \lbrace (a, a), (b, b) \rbrace$ ในชุด $X = \lbrace a, b \rbrace$ เป็นแบบสะท้อนกลับ
เรียกความสัมพันธ์ R บนเซต A Irreflexive ถ้าไม่ $a \in A$ เกี่ยวข้องกับ (aRa ไม่ถือ)
Example - ความสัมพันธ์ $R = \lbrace (a, b), (b, a) \rbrace$ ในชุด $X = \lbrace a, b \rbrace$ ไม่สะท้อนแสง
เรียกความสัมพันธ์ R บนเซต A Symmetric ถ้า $xRy$ หมายถึง $yRx$, $\forall x \in A$ และ $\forall y \in A$.
Example - ความสัมพันธ์ $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ ในชุด $A = \lbrace 1, 2, 3 \rbrace$ เป็นสมมาตร
เรียกความสัมพันธ์ R บนเซต A Anti-Symmetric ถ้า $xRy$ และ $yRx$ หมายถึง $x = y \: \forall x \in A$ และ $\forall y \in A$.
Example - ความสัมพันธ์ $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ เป็นแอนตี้ - สมมาตรตั้งแต่ $x \leq y$ และ $y \leq x$ หมายถึง $x = y$.
เรียกความสัมพันธ์ R บนเซต A Transitive ถ้า $xRy$ และ $yRz$ หมายถึง $xRz, \forall x,y,z \in A$.
Example - ความสัมพันธ์ $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ ในชุด $A = \lbrace 1, 2, 3 \rbrace$ เป็นสกรรมกริยา
ความสัมพันธ์คือไฟล์ Equivalence Relation ถ้ามันเป็นแบบสะท้อนสมมาตรและสกรรมกริยา
Example - ความสัมพันธ์ $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ ในชุด $A = \lbrace 1, 2, 3 \rbrace$ เป็นความสัมพันธ์ที่เท่าเทียมกันเนื่องจากเป็นแบบรีเฟลกซ์สมมาตรและสกรรมกริยา
ก Functionกำหนดให้กับแต่ละองค์ประกอบของชุดหนึ่งองค์ประกอบของชุดที่เกี่ยวข้อง ฟังก์ชันค้นหาแอปพลิเคชันของตนในสาขาต่างๆเช่นการแสดงความซับซ้อนในการคำนวณของอัลกอริทึมการนับวัตถุการศึกษาลำดับและสตริงเพื่อตั้งชื่อไม่กี่ บทที่สามและสุดท้ายของส่วนนี้เน้นถึงลักษณะสำคัญของฟังก์ชัน
ฟังก์ชัน - คำจำกัดความ
ฟังก์ชันหรือการทำแผนที่ (กำหนดเป็น $f: X \rightarrow Y$) คือความสัมพันธ์จากองค์ประกอบของชุดหนึ่ง X ไปยังองค์ประกอบของอีกชุดหนึ่ง Y (X และ Y เป็นชุดที่ไม่ว่างเปล่า) X เรียกว่าโดเมนและ Y เรียกว่า Codomain ของฟังก์ชัน 'f'
ฟังก์ชัน 'f' คือความสัมพันธ์ของ X และ Y สำหรับแต่ละฟังก์ชัน $x \in X$มีอยู่ไม่ซ้ำกัน $y \in Y$ ดังนั้น $(x,y) \in R$. 'x' เรียกว่า pre-image และ 'y' เรียกว่า image of function f
ฟังก์ชันสามารถเป็นหนึ่งต่อหนึ่งหรือหลายต่อหนึ่ง แต่ไม่ใช่ฟังก์ชันหนึ่งต่อหลาย
ฟังก์ชัน Injective / One-to-one
ฟังก์ชั่น $f: A \rightarrow B$ คือฟังก์ชั่นการฉีดหรือตัวต่อตัวถ้าสำหรับทุกๆ $b \in B$มีอยู่มากที่สุดหนึ่งรายการ $a \in A$ ดังนั้น $f(s) = t$.
ซึ่งหมายถึงฟังก์ชัน f เป็นแบบฉีดถ้า $a_1 \ne a_2$ หมายถึง $f(a1) \ne f(a2)$.
ตัวอย่าง
$f: N \rightarrow N, f(x) = 5x$ เป็นแบบฉีด
$f: N \rightarrow N, f(x) = x^2$ เป็นแบบฉีด
$f: R\rightarrow R, f(x) = x^2$ ไม่ฉีดเป็น $(-x)^2 = x^2$
ฟังก์ชัน Surjective / Onto
ฟังก์ชั่น $f: A \rightarrow B$จะคาดเดา (ไปยัง) ถ้าภาพของ f เท่ากับช่วง เทียบเท่ากับทุกๆ$b \in B$มีอยู่บ้าง $a \in A$ ดังนั้น $f(a) = b$. ซึ่งหมายความว่าสำหรับ y ใด ๆ ใน B จะมี x อยู่ใน A เช่นนั้น$y = f(x)$.
ตัวอย่าง
$f : N \rightarrow N, f(x) = x + 2$ เป็นการคาดเดา
$f : R \rightarrow R, f(x) = x^2$ ไม่ใช่การคาดเดาเนื่องจากเราไม่สามารถหาจำนวนจริงที่กำลังสองเป็นลบ
Bijective / One-to-one Correspondent
ฟังก์ชั่น $f: A \rightarrow B$ เป็นผู้สื่อข่าวแบบไบเจ็กต์หรือแบบตัวต่อตัวในกรณีที่ f มีทั้งแบบฉีดและแบบผ่าตัด
ปัญหา
พิสูจน์ว่าฟังก์ชั่น $f: R \rightarrow R$ ที่กำหนดโดย $f(x) = 2x – 3$ เป็นฟังก์ชัน bijective
Explanation - เราต้องพิสูจน์ว่าฟังก์ชั่นนี้มีทั้งแบบฉีดและแบบคาดเดา
ถ้า $f(x_1) = f(x_2)$แล้ว $2x_1 – 3 = 2x_2 – 3 $ และมันก็บอกเป็นนัยว่า $x_1 = x_2$.
ดังนั้น f คือ injective.
ที่นี่ $2x – 3= y$
ดังนั้น, $x = (y+5)/3$ ซึ่งเป็นของ R และ $f(x) = y$.
ดังนั้น f คือ surjective.
ตั้งแต่ f เป็นทั้งสองอย่าง surjective และ injectiveเราสามารถพูดได้ f คือ bijective.
ผกผันของฟังก์ชัน
inverse ของฟังก์ชันที่เกี่ยวข้องแบบหนึ่งต่อหนึ่ง $f : A \rightarrow B$คือฟังก์ชัน $g : B \rightarrow A$ถือครองทรัพย์สินดังต่อไปนี้ -
$f(x) = y \Leftrightarrow g(y) = x$
ฟังก์ชัน f ถูกเรียกใช้ invertibleถ้ามีฟังก์ชันผกผัน g อยู่
ตัวอย่าง
ฟังก์ชั่น $f : Z \rightarrow Z, f(x)=x+5$จะกลับด้านได้เนื่องจากมีฟังก์ชันผกผัน $ g : Z \rightarrow Z, g(x)= x-5$.
ฟังก์ชั่น $f : Z \rightarrow Z, f(x)=x^2$ ไม่สามารถกลับรายการได้เนื่องจากไม่ใช่แบบตัวต่อตัว $(-x)^2=x^2$.
องค์ประกอบของฟังก์ชัน
สองฟังก์ชั่น $f: A \rightarrow B$ และ $g: B \rightarrow C$ สามารถประกอบเพื่อให้องค์ประกอบ $g o f$. นี่คือฟังก์ชันจาก A ถึง C ที่กำหนดโดย$(gof)(x) = g(f(x))$
ตัวอย่าง
ปล่อย $f(x) = x + 2$ และ $g(x) = 2x + 1$, ค้นหา $( f o g)(x)$ และ $( g o f)(x)$.
วิธีการแก้
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
ดังนั้น $(f o g)(x) \neq (g o f)(x)$
ข้อเท็จจริงบางประการเกี่ยวกับองค์ประกอบ
ถ้า f และ g เป็นแบบหนึ่งต่อหนึ่งฟังก์ชัน $(g o f)$ ยังเป็นแบบตัวต่อตัว
ถ้า f และ g อยู่บนฟังก์ชัน $(g o f)$ ยังเข้าสู่
การจัดองค์ประกอบถือทรัพย์สินที่เชื่อมโยงกันเสมอ แต่ไม่ถือคุณสมบัติที่สับเปลี่ยน
กฎของตรรกะทางคณิตศาสตร์ระบุวิธีการให้เหตุผลข้อความทางคณิตศาสตร์ อริสโตเติลนักปรัชญาชาวกรีกเป็นผู้บุกเบิกการหาเหตุผลเชิงตรรกะ การให้เหตุผลเชิงตรรกะเป็นพื้นฐานทางทฤษฎีสำหรับคณิตศาสตร์หลาย ๆ ด้านและตามมาด้วยวิทยาศาสตร์คอมพิวเตอร์ มีการประยุกต์ใช้งานจริงมากมายในวิทยาการคอมพิวเตอร์เช่นการออกแบบเครื่องคอมพิวเตอร์ปัญญาประดิษฐ์ความหมายของโครงสร้างข้อมูลสำหรับภาษาโปรแกรมเป็นต้น
Propositional Logicเกี่ยวข้องกับข้อความที่สามารถกำหนดค่าความจริง "จริง" และ "เท็จ" ได้ จุดประสงค์คือเพื่อวิเคราะห์ข้อความเหล่านี้ไม่ว่าจะเป็นรายบุคคลหรือแบบประกอบ
Prepositional Logic - คำจำกัดความ
ประพจน์คือชุดของข้อความประกาศที่มีทั้งค่าความจริง "จริง" หรือค่าความจริง "เท็จ" ประพจน์ประกอบด้วยตัวแปรเชิงประพจน์และตัวเชื่อมเราแสดงตัวแปรเชิงประพจน์ด้วยตัวพิมพ์ใหญ่ (A, B, ฯลฯ ) Connectives เชื่อมต่อตัวแปรเชิงประพจน์
ตัวอย่างบางส่วนของข้อเสนอมีให้ด้านล่าง -
- "มนุษย์เป็นมนุษย์" จะส่งกลับค่าความจริง "TRUE"
- "12 + 9 = 3 - 2" จะส่งกลับค่าความจริง "FALSE"
ต่อไปนี้ไม่ใช่ข้อเสนอ -
"A น้อยกว่า 2" เป็นเพราะถ้าเราไม่ให้ค่าเฉพาะของ A เราไม่สามารถบอกได้ว่าข้อความนั้นเป็นจริงหรือเท็จ
Connectives
ในตรรกะเชิงประพจน์โดยทั่วไปเราใช้การเชื่อมต่อห้าแบบซึ่ง ได้แก่ -
หรือ ($\lor$)
และ ($\land$)
การปฏิเสธ / ไม่ ($\lnot$)
นัย / ถ้า - แล้ว ($\rightarrow$)
ถ้าและเฉพาะในกรณีที่ ($\Leftrightarrow$).
OR ($\lor$) - การดำเนินการหรือของสองประพจน์ A และ B (เขียนเป็น $A \lor B$) เป็นจริงถ้าตัวแปรประพจน์ A หรือ B เป็นจริงอย่างน้อยที่สุด
ตารางความจริงมีดังนี้ -
| ก | ข | ก∨ข |
|---|---|---|
| จริง | จริง | จริง |
| จริง | เท็จ | จริง |
| เท็จ | จริง | จริง |
| เท็จ | เท็จ | เท็จ |
AND ($\land$) - การดำเนินการ AND ของสองประพจน์ A และ B (เขียนเป็น $A \land B$) จะเป็นจริงถ้าทั้งตัวแปรประพจน์ A และ B เป็นจริง
ตารางความจริงมีดังนี้ -
| ก | ข | ก∧ข |
|---|---|---|
| จริง | จริง | จริง |
| จริง | เท็จ | เท็จ |
| เท็จ | จริง | เท็จ |
| เท็จ | เท็จ | เท็จ |
Negation ($\lnot$) - การปฏิเสธของโจทย์ A (เขียนเป็น $\lnot A$) เป็นเท็จเมื่อ A เป็นจริงและเป็นจริงเมื่อ A เป็นเท็จ
ตารางความจริงมีดังนี้ -
| ก | ¬ก |
|---|---|
| จริง | เท็จ |
| เท็จ | จริง |
Implication / if-then ($\rightarrow$) - ความหมาย $A \rightarrow B$คือโจทย์“ ถ้า A แล้ว B” เป็นเท็จถ้า A เป็นจริงและ B เป็นเท็จ กรณีที่เหลือเป็นเรื่องจริง
ตารางความจริงมีดังนี้ -
| ก | ข | ก→ข |
|---|---|---|
| จริง | จริง | จริง |
| จริง | เท็จ | เท็จ |
| เท็จ | จริง | จริง |
| เท็จ | เท็จ | จริง |
If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ เป็นความเชื่อมโยงทางตรรกะแบบสองเงื่อนไขซึ่งเป็นจริงเมื่อ p และ q เหมือนกันกล่าวคือทั้งสองเป็นเท็จหรือทั้งสองเป็นจริง
ตารางความจริงมีดังนี้ -
| ก | ข | ก⇔ข |
|---|---|---|
| จริง | จริง | จริง |
| จริง | เท็จ | เท็จ |
| เท็จ | จริง | เท็จ |
| เท็จ | เท็จ | จริง |
Tautologies
Tautology เป็นสูตรที่เป็นจริงสำหรับทุกค่าของตัวแปรเชิงประพจน์
Example - พิสูจน์ $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ เป็น tautology
ตารางความจริงมีดังนี้ -
| ก | ข | ก→ข | (A → B) ∧ก | [(A → B) ∧ A] → B |
|---|---|---|---|---|
| จริง | จริง | จริง | จริง | จริง |
| จริง | เท็จ | เท็จ | เท็จ | จริง |
| เท็จ | จริง | จริง | เท็จ | จริง |
| เท็จ | เท็จ | จริง | เท็จ | จริง |
อย่างที่เราเห็นค่าของ $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ คือ "จริง" มันเป็นความตึงเครียด
ความขัดแย้ง
ความขัดแย้งคือสูตรที่มักจะเป็นเท็จสำหรับทุกค่าของตัวแปรเชิงประพจน์
Example - พิสูจน์ $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ เป็นความขัดแย้ง
ตารางความจริงมีดังนี้ -
| ก | ข | ก∨ข | ¬ก | ¬ข | (¬ A) ∧ (¬ B) | (A ∨ B) ∧ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| จริง | จริง | จริง | เท็จ | เท็จ | เท็จ | เท็จ |
| จริง | เท็จ | จริง | เท็จ | จริง | เท็จ | เท็จ |
| เท็จ | จริง | จริง | จริง | เท็จ | เท็จ | เท็จ |
| เท็จ | เท็จ | เท็จ | จริง | จริง | จริง | เท็จ |
อย่างที่เราเห็นค่าของ $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ เป็น "เท็จ" มันเป็นความขัดแย้ง
ฉุกเฉิน
Contingency คือสูตรที่มีทั้งค่าจริงและค่าเท็จสำหรับทุกค่าของตัวแปรเชิงประพจน์
Example - พิสูจน์ $(A \lor B) \land (\lnot A)$ กรณีฉุกเฉิน
ตารางความจริงมีดังนี้ -
| ก | ข | ก∨ข | ¬ก | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| จริง | จริง | จริง | เท็จ | เท็จ |
| จริง | เท็จ | จริง | เท็จ | เท็จ |
| เท็จ | จริง | จริง | จริง | จริง |
| เท็จ | เท็จ | เท็จ | จริง | เท็จ |
อย่างที่เราเห็นค่าของ $(A \lor B) \land (\lnot A)$ มีทั้ง“ จริง” และ“ เท็จ” เป็นเหตุฉุกเฉิน
Propositional Equivalences
สองคำสั่ง X และ Y มีความเท่าเทียมกันทางตรรกะหากมีเงื่อนไขสองข้อต่อไปนี้ -
ตารางความจริงของแต่ละคำสั่งมีค่าความจริงเหมือนกัน
คำสั่งสองเงื่อนไข $X \Leftrightarrow Y$ เป็น tautology
Example - พิสูจน์ $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ เทียบเท่า
การทดสอบโดยวิธี1 st (ตารางความจริงที่ตรงกัน)
| ก | ข | ก∨ข | ¬ (A ∨ B) | ¬ก | ¬ข | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| จริง | จริง | จริง | เท็จ | เท็จ | เท็จ | เท็จ |
| จริง | เท็จ | จริง | เท็จ | เท็จ | จริง | เท็จ |
| เท็จ | จริง | จริง | เท็จ | จริง | เท็จ | เท็จ |
| เท็จ | เท็จ | เท็จ | จริง | จริง | จริง | จริง |
ที่นี่เราจะเห็นค่าความจริงของ $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ เหมือนกันดังนั้นงบจึงเทียบเท่ากัน
การทดสอบ 2 ครั้งวิธีการ (Bi-conditionality)
| ก | ข | ¬ (A ∨ B) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|
| จริง | จริง | เท็จ | เท็จ | จริง |
| จริง | เท็จ | เท็จ | เท็จ | จริง |
| เท็จ | จริง | เท็จ | เท็จ | จริง |
| เท็จ | เท็จ | จริง | จริง | จริง |
เช่น $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ เป็น tautology งบเทียบเท่า
ผกผัน Converse และ Contra-positive
นัย / ถ้า - แล้ว $(\rightarrow)$เรียกอีกอย่างว่าคำสั่งเงื่อนไข มีสองส่วน -
- สมมติฐาน, น
- สรุป q
ดังที่ได้กล่าวไว้ก่อนหน้านี้แสดงว่าเป็น $p \rightarrow q$.
Example of Conditional Statement-“ ถ้าคุณทำการบ้านคุณจะไม่ถูกลงโทษ” ที่นี่ "คุณทำการบ้าน" คือสมมุติฐาน p และ "คุณจะไม่ถูกลงโทษ" คือข้อสรุป q
Inverse- การผกผันของคำสั่งเงื่อนไขคือการปฏิเสธของทั้งสมมติฐานและข้อสรุป ถ้าคำสั่งคือ“ ถ้า p แล้ว q” ค่าผกผันจะเป็น“ ถ้าไม่ใช่ p แล้วไม่ใช่ q” ดังนั้นผกผันของ$p \rightarrow q$ คือ $ \lnot p \rightarrow \lnot q$.
Example - สิ่งที่ตรงกันข้ามของ“ ถ้าคุณทำการบ้านคุณจะไม่ถูกลงโทษ” คือ“ ถ้าคุณไม่ทำการบ้านคุณจะถูกลงโทษ”
Converse- การสนทนาของคำสั่งเงื่อนไขคำนวณโดยการแลกเปลี่ยนสมมติฐานและข้อสรุป ถ้าคำสั่งคือ“ ถ้า p แล้ว q” การสนทนาจะเป็น“ ถ้า q แล้ว p” สนทนาของ$p \rightarrow q$ คือ $q \rightarrow p$.
Example - บทสนทนาของ "ถ้าคุณทำการบ้านคุณจะไม่ถูกลงโทษ" คือ "ถ้าคุณไม่ถูกลงโทษคุณทำการบ้านของคุณ"
Contra-positive- ผลตรงกันข้ามของเงื่อนไขคำนวณโดยการแลกเปลี่ยนสมมติฐานและข้อสรุปของคำสั่งผกผัน ถ้าคำสั่งคือ "ถ้า p แล้ว q" ผลตรงกันข้ามจะเป็น "ถ้าไม่ใช่ q แล้วไม่ใช่ p" ตรงกันข้ามของ$p \rightarrow q$ คือ $\lnot q \rightarrow \lnot p$.
Example - ข้อตรงกันข้ามของ "ถ้าคุณทำการบ้านคุณจะไม่ถูกลงโทษ" คือ "ถ้าคุณถูกลงโทษคุณไม่ได้ทำการบ้านของคุณ"
หลักการคู่
หลักการความเป็นคู่ระบุว่าสำหรับคำสั่งจริงใด ๆ คำสั่งคู่ที่ได้จากการเปลี่ยนสหภาพเป็นทางแยก (และในทางกลับกัน) และการเปลี่ยนชุดสากลเป็นชุด Null (และในทางกลับกัน) ก็เป็นจริงเช่นกัน หากคู่ของคำสั่งใด ๆ เป็นคำสั่งนั้นเองก็มีการกล่าวself-dual คำให้การ.
Example - คู่ของ $(A \cap B ) \cup C$ คือ $(A \cup B) \cap C$
แบบฟอร์มปกติ
เราสามารถแปลงประพจน์ใดก็ได้ในสองรูปแบบปกติ -
- รูปแบบปกติ Conjunctive
- รูปแบบปกติที่ไม่ต่อเนื่อง
รูปแบบปกติ Conjunctive
คำสั่งผสมอยู่ในรูปแบบปกติร่วมกันถ้าได้มาจากการดำเนินการและระหว่างตัวแปร (การปฏิเสธของตัวแปรที่รวมอยู่) ที่เชื่อมต่อกับ OR ในแง่ของการดำเนินการเซ็ตมันเป็นคำสั่งผสมที่ได้จากการแยกระหว่างตัวแปรที่เชื่อมต่อกับสหภาพแรงงาน
Examples
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
รูปแบบปกติที่ไม่ต่อเนื่อง
คำสั่งผสมอยู่ในรูปแบบปกติที่ไม่ต่อเนื่องหากได้มาจากการดำเนินการหรือระหว่างตัวแปร (การปฏิเสธของตัวแปรที่รวมอยู่) ที่เชื่อมต่อกับ ANDs ในแง่ของการดำเนินการเซ็ตมันเป็นคำสั่งผสมที่ได้รับจากยูเนี่ยนระหว่างตัวแปรที่เชื่อมต่อกับทางแยก
Examples
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
Predicate Logic เกี่ยวข้องกับเพรดิเคตซึ่งเป็นประพจน์ที่มีตัวแปร
Predicate Logic - คำจำกัดความ
เพรดิเคตคือนิพจน์ของตัวแปรตั้งแต่หนึ่งตัวขึ้นไปที่กำหนดบนโดเมนเฉพาะบางโดเมน เพรดิเคตที่มีตัวแปรสามารถสร้างเป็นประพจน์ได้โดยการกำหนดค่าให้กับตัวแปรหรือโดยการหาจำนวนตัวแปร
ต่อไปนี้เป็นตัวอย่างบางส่วนของเพรดิเคต -
- ให้ E (x, y) แสดงว่า "x = y"
- ให้ X (a, b, c) แสดงว่า "a + b + c = 0"
- ให้ M (x, y) แสดงว่า "x แต่งงานกับ y"
สูตรที่สร้างขึ้นอย่างดี
Well Formed Formula (wff) เป็นเพรดิเคตที่มีสิ่งต่อไปนี้ -
ค่าคงที่เชิงประพจน์และตัวแปรเชิงประพจน์ทั้งหมดเป็น wffs
ถ้า x เป็นตัวแปรและ Y คือ wff $\forall x Y$ และ $\exists x Y$ ยังมี wff
ค่าความจริงและค่าเท็จเป็น wffs
สูตรอะตอมแต่ละสูตรคือ wff
การเชื่อมต่อทั้งหมดที่เชื่อมต่อ wffs เป็น wffs
Quantifiers
ตัวแปรของเพรดิเคตถูกหาค่าโดยตัวระบุปริมาณ มีตัวระบุสองประเภทในลอจิกเพรดิเคต - Universal Quantifier และ Existential Quantifier
Universal Quantifier
Universal quantifier ระบุว่าคำสั่งภายในขอบเขตเป็นจริงสำหรับทุกค่าของตัวแปรเฉพาะ มันแสดงด้วยสัญลักษณ์$\forall$.
$\forall x P(x)$ ถูกอ่านเป็นค่า x ทุกค่า P (x) เป็นจริง
Example - "มนุษย์เป็นมรรตัย" สามารถเปลี่ยนเป็นรูปแบบประพจน์ได้ $\forall x P(x)$ โดยที่ P (x) คือเพรดิเคตที่แสดงว่า x เป็นมนุษย์และจักรวาลของวาทกรรมคือผู้ชายทั้งหมด
ตัวบ่งชี้ที่มีอยู่
Existential quantifier ระบุว่าข้อความภายในขอบเขตเป็นจริงสำหรับค่าบางค่าของตัวแปรเฉพาะ มันแสดงด้วยสัญลักษณ์$\exists $.
$\exists x P(x)$ ถูกอ่านเป็นค่า x บางค่า P (x) เป็นจริง
Example - "บางคนไม่ซื่อสัตย์" สามารถเปลี่ยนเป็นแบบโจทย์ได้ $\exists x P(x)$ โดยที่ P (x) เป็นเพรดิเคตที่แสดงว่า x ไม่ซื่อสัตย์และจักรวาลของวาทกรรมคือบางคน
Quantifier ที่ซ้อนกัน
หากเราใช้ตัวระบุปริมาณที่ปรากฏภายในขอบเขตของตัวระบุตัวระบุอื่นจะเรียกว่าตัวระบุจำนวนที่ซ้อนกัน
Example
$\forall\ a\: \exists b\: P (x, y)$ ที่ไหน $P (a, b)$ หมายถึง $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ ที่ไหน $P (a, b)$ หมายถึง $a + (b + c) = (a + b) + c$
Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
เพื่อสรุปข้อความใหม่จากข้อความที่มีความจริงที่เรารู้อยู่แล้ว Rules of Inference ใช้
กฎการอนุมานมีไว้เพื่ออะไร?
ตรรกะทางคณิตศาสตร์มักใช้สำหรับการพิสูจน์เชิงตรรกะ การพิสูจน์เป็นอาร์กิวเมนต์ที่ถูกต้องซึ่งกำหนดค่าความจริงของข้อความทางคณิตศาสตร์
อาร์กิวเมนต์คือลำดับของคำสั่ง คำสั่งสุดท้ายคือข้อสรุปและข้อความก่อนหน้าทั้งหมดเรียกว่าสถานที่ (หรือสมมติฐาน) สัญลักษณ์ "$\therefore$”, (อ่านดังนั้น) วางไว้ก่อนข้อสรุป อาร์กิวเมนต์ที่ถูกต้องคือข้อสรุปที่ตามมาจากค่าความจริงของสถานที่
กฎของการอนุมานเป็นแม่แบบหรือแนวทางในการสร้างข้อโต้แย้งที่ถูกต้องจากข้อความที่เรามีอยู่แล้ว
ตารางกฎการอนุมาน
| กฎการอนุมาน | ชื่อ | กฎการอนุมาน | ชื่อ |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
ส่วนที่เพิ่มเข้าไป |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
Syllogism ที่ไม่สอดคล้องกัน |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
คำสันธาน |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
Syllogism สมมุติ |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
การทำให้เข้าใจง่าย |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
Constructive Dilemma |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
โมดัสพอนส์ |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
Dilemma ทำลายล้าง |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
Modus Tollens |
ส่วนที่เพิ่มเข้าไป
ถ้า P เป็นหลักฐานเราสามารถใช้กฎการเพิ่มเพื่อได้มา $ P \lor Q $.
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
ตัวอย่าง
ให้ P เป็นโจทย์ว่า“ เขาเรียนหนักมาก” เป็นเรื่องจริง
ดังนั้น - "ไม่ว่าเขาจะเรียนหนักมากหรือเขาเป็นนักเรียนที่แย่มาก" นี่คือโจทย์ Q "เขาเป็นนักเรียนที่แย่มาก"
คำสันธาน
ถ้า P และ Q เป็นสองสถานที่เราสามารถใช้กฎ Conjunction เพื่อให้ได้มา $ P \land Q $.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
ตัวอย่าง
ให้ P -“ เขาเรียนหนักมาก”
ให้ถาม -“ เขาเป็นเด็กดีที่สุดในชั้นเรียน”
ดังนั้น - "เขาเรียนหนักมากและเขาเป็นเด็กที่เก่งที่สุดในชั้นเรียน"
การทำให้เข้าใจง่าย
ถ้า $P \land Q$ เป็นหลักฐานเราสามารถใช้กฎการทำให้เข้าใจง่ายเพื่อให้ได้มาซึ่ง P.
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
ตัวอย่าง
"เขาเรียนหนักมากและเขาเป็นเด็กที่เก่งที่สุดในชั้นเรียน", $P \land Q$
ดังนั้น - "เขาเรียนหนักมาก"
โมดัสพอนส์
ถ้า P และ $P \rightarrow Q$ เป็นสองสถานที่เราสามารถใช้ Modus Ponens เพื่อรับ Q.
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
ตัวอย่าง
"หากคุณมีรหัสผ่านคุณสามารถเข้าสู่ Facebook ได้", $P \rightarrow Q$
"คุณมีรหัสผ่าน", P
ดังนั้น - "คุณสามารถเข้าสู่ระบบ facebook"
Modus Tollens
ถ้า $P \rightarrow Q$ และ $\lnot Q$ เป็นสองสถานที่เราสามารถใช้ Modus Tollens เพื่อรับ $\lnot P$.
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You cannot log on to facebook", $\lnot Q$
Therefore − "You do not have a password "
Disjunctive Syllogism
If $\lnot P$ and $P \lor Q$ are two premises, we can use Disjunctive Syllogism to derive Q.
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
Example
"The ice cream is not vanilla flavored", $\lnot P$
"The ice cream is either vanilla flavored or chocolate flavored", $P \lor Q$
Therefore − "The ice cream is chocolate flavored”
Hypothetical Syllogism
If $P \rightarrow Q$ and $Q \rightarrow R$ are two premises, we can use Hypothetical Syllogism to derive $P \rightarrow R$
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
Example
"If it rains, I shall not go to school”, $P \rightarrow Q$
"If I don't go to school, I won't need to do homework", $Q \rightarrow R$
Therefore − "If it rains, I won't need to do homework"
Constructive Dilemma
If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
Example
“If it rains, I will take a leave”, $( P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either it will rain or it is hot outside”, $P \lor R$
Therefore − "I will take a leave or I will go for a shower"
Destructive Dilemma
If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
Example
“If it rains, I will take a leave”, $(P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either I will not take a leave or I will not go for a shower”, $\lnot Q \lor \lnot S$
Therefore − "Either it does not rain or it is not hot outside"
Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.
In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −
“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”
In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.
Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.
A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.
The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −
Closure
A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.
Example
Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.
The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.
Associative Laws
A binary operator $\otimes$ on a set A is associative when it holds the following property −
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.
The operator minus $( - )$ is not associative since
$$( x - y ) - z \ne x - ( y - z )$$
Commutative Laws
A binary operator $\otimes$ on a set A is commutative when it holds the following property −
$x \otimes y = y \otimes x$, ที่ไหน $x, y \in A$
ตัวอย่าง
ปล่อย $A = \lbrace 1, 2, 3, 4 \rbrace$
ตัวดำเนินการบวก $( + )$ เป็นสับเปลี่ยนเพราะสำหรับสององค์ประกอบใด ๆ $x,y \in A$, ทรัพย์สิน $x + y = y + x$ ถือ
ตัวดำเนินการลบ $( - )$ ไม่เชื่อมโยงตั้งแต่
$$x - y \ne y - x$$
กฎหมายการจัดจำหน่าย
ตัวดำเนินการไบนารีสองตัว $\otimes$ และ $\circledast$ ในชุด A จะกระจายผ่านตัวดำเนินการ $\circledast$ เมื่อทรัพย์สินต่อไปนี้ถือ -
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, ที่ไหน $x, y, z \in A $
ตัวอย่าง
ปล่อย $A = \lbrace 1, 2, 3, 4 \rbrace$
ตัวดำเนินการเข้า $( * )$ และบวก $( + )$ มีการกระจายมากกว่าตัวดำเนินการ + เพราะสำหรับองค์ประกอบทั้งสาม $x,y,z \in A$, ทรัพย์สิน $x * ( y + z ) = ( x * y ) + ( x * z )$ ถือ
อย่างไรก็ตามตัวดำเนินการเหล่านี้ไม่ได้กระจายไป $*$ ตั้งแต่
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
องค์ประกอบประจำตัว
ชุด A มีองค์ประกอบประจำตัวที่เกี่ยวข้องกับการดำเนินการไบนารี $\otimes$ บน A หากมีองค์ประกอบ $e \in A$เพื่อให้ทรัพย์สินต่อไปนี้ถือ -
$e \otimes x = x \otimes e$, ที่ไหน $x \in A$
ตัวอย่าง
ปล่อย $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
องค์ประกอบที่ 1 เป็นองค์ประกอบเอกลักษณ์ที่เกี่ยวข้องกับการดำเนินการ $*$ ตั้งแต่สำหรับองค์ประกอบใด ๆ $x \in Z$,
$$1 * x = x * 1$$
ในทางกลับกันไม่มีองค์ประกอบเอกลักษณ์สำหรับการดำเนินการลบ $( - )$
ผกผัน
หากชุด A มีองค์ประกอบประจำตัว $e$ เกี่ยวกับตัวดำเนินการไบนารี $\otimes $กล่าวกันว่ามีการผกผันเมื่อใดก็ตามสำหรับทุกองค์ประกอบ $x \in A$มีองค์ประกอบอื่นอยู่ $y \in A$เพื่อให้ทรัพย์สินต่อไปนี้ถือ -
$$x \otimes y = e$$
ตัวอย่าง
ปล่อย $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
ให้การดำเนินการบวก $( + )$ และ $e = 0$ผกผันขององค์ประกอบ x คือ $(-x)$ ตั้งแต่ $x + (x) = 0$
กฎของเดอมอร์แกน
กฎของเดอมอร์แกนให้การเปลี่ยนแปลงระหว่างสหภาพและจุดตัดของสองชุด (หรือมากกว่า) ในแง่ของการเติมเต็ม กฎหมายคือ -
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
ตัวอย่าง
ปล่อย $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$และ
ชุดสากล $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
ดังนั้นเราจึงเห็นว่า $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
ดังนั้นเราจึงเห็นว่า $(A \cap B)' = A' \cup B'$
กลุ่มย่อย
เซต จำกัด หรือไม่สิ้นสุด $‘S’$ ด้วยการดำเนินการไบนารี $‘\omicron’$ (Composition) เรียกว่าเซมิกรุ๊ปหากมีสองเงื่อนไขพร้อมกัน -
Closure - สำหรับทุกคู่ $(a, b) \in S, \:(a \omicron b)$ จะต้องมีอยู่ในชุด $S$.
Associative - สำหรับทุกองค์ประกอบ $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ ต้องถือ
ตัวอย่าง
เซตของจำนวนเต็มบวก (ไม่รวมศูนย์) ที่มีการดำเนินการบวกคือเซมิกรุ๊ป ตัวอย่างเช่น,$ S = \lbrace 1, 2, 3, \dots \rbrace $
คุณสมบัติการปิดที่นี่ถือเป็นสำหรับทุกคู่ $(a, b) \in S, (a + b)$ มีอยู่ในเซต S ตัวอย่างเช่น $1 + 2 = 3 \in S]$
คุณสมบัติ Associative ยังถือสำหรับทุกองค์ประกอบ $a, b, c \in S, (a + b) + c = a + (b + c)$. ตัวอย่างเช่น,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
Monoid
monoid คือเซมิกรุ๊ปที่มีองค์ประกอบเอกลักษณ์ องค์ประกอบเอกลักษณ์ (แสดงโดย$e$ หรือ E) ของเซต S เป็นองค์ประกอบเช่นนั้น $(a \omicron e) = a$สำหรับทุกองค์ประกอบ $a \in S$. องค์ประกอบเอกลักษณ์เรียกอีกอย่างว่าไฟล์unit element. ดังนั้น monoid จึงมีคุณสมบัติสามอย่างพร้อมกัน -Closure, Associative, Identity element.
ตัวอย่าง
ชุดของจำนวนเต็มบวก (ไม่รวมศูนย์) ที่มีการดำเนินการคูณเป็น monoid $S = \lbrace 1, 2, 3, \dots \rbrace $
คุณสมบัติการปิดที่นี่ถือเป็นสำหรับทุกคู่ $(a, b) \in S, (a \times b)$ มีอยู่ในเซต S. [ตัวอย่างเช่น $1 \times 2 = 2 \in S$ และอื่น ๆ ]
คุณสมบัติ Associative ยังถือสำหรับทุกองค์ประกอบ $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [ตัวอย่างเช่น, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ และอื่น ๆ ]
คุณสมบัติประจำตัวยังถือสำหรับทุกองค์ประกอบ $a \in S, (a \times e) = a$ [ตัวอย่างเช่น, $(2 \times 1) = 2, (3 \times 1) = 3$และอื่น ๆ ] องค์ประกอบประจำตัวที่นี่คือ 1
กลุ่ม
กลุ่มคือ monoid ที่มีองค์ประกอบผกผัน องค์ประกอบผกผัน (แสดงโดย I) ของเซต S เป็นองค์ประกอบเช่นนั้น$(a \omicron I) = (I \omicron a) = a$สำหรับแต่ละองค์ประกอบ $a \in S$. ดังนั้นกลุ่มจึงมีคุณสมบัติสี่อย่างพร้อมกัน - i) การปิด, ii) การเชื่อมโยง, iii) องค์ประกอบประจำตัว, iv) องค์ประกอบผกผัน ลำดับของกลุ่ม G คือจำนวนองค์ประกอบใน G และลำดับขององค์ประกอบในกลุ่มเป็นจำนวนเต็มบวกน้อยที่สุด n ซึ่งเป็นองค์ประกอบเอกลักษณ์ของกลุ่ม G นั้น
ตัวอย่าง
ชุดของ $N \times N$ เมทริกซ์ที่ไม่ใช่เอกพจน์สร้างกลุ่มภายใต้การดำเนินการคูณเมทริกซ์
ผลคูณสอง $N \times N$ เมทริกซ์ที่ไม่ใช่เอกพจน์ยังเป็น $N \times N$ เมทริกซ์ที่ไม่ใช่เอกพจน์ซึ่งมีคุณสมบัติการปิด
การคูณเมทริกซ์นั้นเชื่อมโยงกัน ดังนั้นการถือครองทรัพย์สินที่เชื่อมโยงกัน
ชุดของ $N \times N$ เมทริกซ์ที่ไม่ใช่เอกพจน์ประกอบด้วยเมทริกซ์เอกลักษณ์ที่ถือคุณสมบัติองค์ประกอบเอกลักษณ์
เนื่องจากเมทริกซ์ทั้งหมดไม่เป็นเอกพจน์จึงมีองค์ประกอบผกผันซึ่งเป็นเมทริกซ์ที่ไม่เป็นเอกพจน์เช่นกัน ดังนั้นคุณสมบัติผกผันยังถือ
กลุ่มอาเบเลียน
กลุ่ม abelian G คือกลุ่มที่คู่องค์ประกอบ $(a,b) \in G$ถือกฎการสับเปลี่ยนเสมอ ดังนั้นกลุ่มจึงมีคุณสมบัติห้าอย่างพร้อมกัน - i) การปิด, ii) การเชื่อมโยง, iii) องค์ประกอบประจำตัว, iv) องค์ประกอบผกผัน, v) การสับเปลี่ยน
ตัวอย่าง
เซตของจำนวนเต็มบวก (รวมศูนย์) ที่มีการบวกคือกลุ่มเอเบเลียน $G = \lbrace 0, 1, 2, 3, \dots \rbrace$
คุณสมบัติการปิดที่นี่ถือเป็นสำหรับทุกคู่ $(a, b) \in S, (a + b)$ มีอยู่ในเซต S. [ตัวอย่างเช่น $1 + 2 = 2 \in S$ และอื่น ๆ ]
คุณสมบัติ Associative ยังถือสำหรับทุกองค์ประกอบ $a, b, c \in S, (a + b) + c = a + (b + c)$ [ตัวอย่างเช่น, $(1 +2) + 3 = 1 + (2 + 3) = 6$ และอื่น ๆ ]
คุณสมบัติประจำตัวยังถือสำหรับทุกองค์ประกอบ $a \in S, (a \times e) = a$ [ตัวอย่างเช่น, $(2 \times 1) = 2, (3 \times 1) = 3$และอื่น ๆ ] ที่นี่องค์ประกอบประจำตัวคือ 1
คุณสมบัติการสับเปลี่ยนยังถือสำหรับทุกองค์ประกอบ $a \in S, (a \times b) = (b \times a)$ [ตัวอย่างเช่น, $(2 \times 3) = (3 \times 2) = 3$ และอื่น ๆ ]
กลุ่มไซคลิกและกลุ่มย่อย
ก cyclic groupคือกลุ่มที่สามารถสร้างขึ้นโดยองค์ประกอบเดียว ทุกองค์ประกอบของกลุ่มวัฏจักรเป็นพลังขององค์ประกอบเฉพาะบางอย่างซึ่งเรียกว่าเครื่องกำเนิดไฟฟ้า กลุ่มวัฏจักรสามารถสร้างขึ้นโดยเครื่องกำเนิดไฟฟ้า 'g' ซึ่งองค์ประกอบอื่น ๆ ของกลุ่มสามารถเขียนเป็นพลังของเครื่องกำเนิดไฟฟ้า 'g' ได้
ตัวอย่าง
เซตของจำนวนเชิงซ้อน $\lbrace 1,-1, i, -i \rbrace$ ภายใต้การดำเนินการคูณเป็นกลุ่มวัฏจักร
มีเครื่องปั่นไฟสองเครื่อง - $i$ และ $–i$ เช่น $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ และนอกจากนี้ยังมี $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$ซึ่งครอบคลุมองค์ประกอบทั้งหมดของกลุ่ม ดังนั้นจึงเป็นกลุ่มวัฏจักร
Note - ก cyclic groupมักเป็นกลุ่ม abelian แต่ไม่ใช่ทุกกลุ่ม abelian ที่เป็นกลุ่มวัฏจักร ตัวเลขที่เป็นเหตุเป็นผลภายใต้การบวกไม่ได้เป็นแบบวนรอบ แต่เป็นแบบอะเบลเลียน
ก subgroup H เป็นส่วนย่อยของกลุ่ม G (แสดงโดย $H ≤ G$) หากตรงตามคุณสมบัติทั้งสี่พร้อมกัน - Closure, Associative, Identity elementและ Inverse.
กลุ่มย่อย H ของกลุ่ม G ที่ไม่รวมทั้งกลุ่ม G เรียกว่ากลุ่มย่อยที่เหมาะสม (แสดงโดย $H < G$). กลุ่มย่อยของกลุ่มวัฏจักรคือวัฏจักรและกลุ่มย่อยอาเบเลียนก็เป็นอาเบเลียนเช่นกัน
ตัวอย่าง
ให้กลุ่ม $G = \lbrace 1, i, -1, -i \rbrace$
จากนั้นกลุ่มย่อยบางกลุ่มคือ $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
นี่ไม่ใช่กลุ่มย่อย - $H_3 = \lbrace 1, i \rbrace$ เพราะนั่น $(i)^{-1} = -i$ ไม่ได้อยู่ใน $H_3$
ชุดที่สั่งซื้อบางส่วน (POSET)
ชุดที่สั่งซื้อบางส่วนประกอบด้วยชุดที่มีความสัมพันธ์แบบไบนารีซึ่งเป็นแบบรีเฟล็กซีฟแอนตีสเมตริกและสกรรมกริยา "ชุดที่สั่งซื้อบางส่วน" ย่อว่า POSET
ตัวอย่าง
ชุดของจำนวนจริงภายใต้การดำเนินการไบนารีน้อยกว่าหรือเท่ากับ $(\le)$ เป็น poset
ปล่อยให้ชุด $S = \lbrace 1, 2, 3 \rbrace$ และการดำเนินการคือ $\le$
ความสัมพันธ์จะเป็น $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
ความสัมพันธ์ R นี้สะท้อนกลับเป็น $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
ความสัมพันธ์ R นี้ต่อต้านสมมาตรเช่นเดียวกับ
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$
ความสัมพันธ์ R นี้ยังเป็นสกรรมกริยาเช่นกัน $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.
ดังนั้นจึงเป็น poset.
ชุดจุดยอดของกราฟ acyclic ที่กำหนดทิศทางภายใต้การดำเนินการ 'ความสามารถในการเข้าถึง' เป็นตำแหน่ง
แผนภาพ Hasse
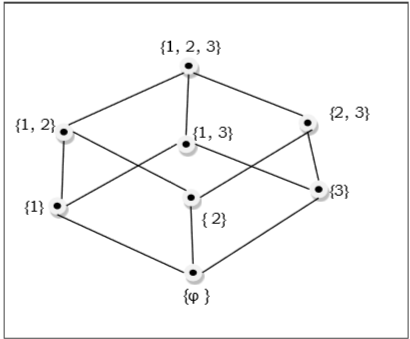
แผนภาพ Hasse ของโพเซ็ตคือกราฟกำกับซึ่งจุดยอดเป็นองค์ประกอบของโพเซตนั้นและส่วนโค้งจะครอบคลุมคู่ (x, y) ในโพเซต ถ้าอยู่ในตำแหน่ง$x < y$จากนั้นจุด x จะปรากฏต่ำกว่าจุด y ในแผนภาพ Hasse ถ้า$x<y<z$ ในตำแหน่งแล้วลูกศรจะไม่แสดงระหว่าง x และ z เนื่องจากเป็นนัย
ตัวอย่าง
ตำแหน่งของเซตย่อยของ $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ แสดงโดยแผนภาพ Hasse ต่อไปนี้ -
ชุดตามลำดับ
ชุดคำสั่งเชิงเส้นหรือชุดที่สั่งซื้อทั้งหมดคือชุดคำสั่งบางส่วนซึ่งทุกคู่ขององค์ประกอบสามารถเปรียบเทียบกันได้ องค์ประกอบ$a, b \in S$ กล่าวกันว่าเปรียบได้ถ้าอย่างใดอย่างหนึ่ง $a \le b$ หรือ $b \le a$ถือ กฎหมาย Trichotomy กำหนดชุดที่สั่งซื้อทั้งหมดนี้ ชุดที่สั่งซื้อทั้งหมดสามารถกำหนดได้ว่าเป็นตาข่ายแบบกระจายที่มีคุณสมบัติ$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ สำหรับค่าทั้งหมดของ a และ b ในชุด S
ตัวอย่าง
ชุดอำนาจของ $\lbrace a, b \rbrace$ เรียงลำดับโดย \ subseteq คือชุดที่เรียงลำดับโดยสิ้นเชิงเป็นองค์ประกอบทั้งหมดของชุดพลังงาน $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ เปรียบได้
ตัวอย่างชุดคำสั่งซื้อที่ไม่ใช่ยอดรวม
ชุด $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ ภายใต้การดำเนินการ x หาร y ไม่ใช่ชุดที่สั่งซื้อทั้งหมด
ที่นี่สำหรับทุกคน $(x, y) \in S, x | y$ต้องถือไว้ แต่ 2 3 เนื่องจาก 2 ไม่หาร 3 หรือ 3 ไม่หาร 2 ดังนั้นจึงไม่ใช่ชุดที่สั่งทั้งหมด
ตาข่าย
ตาข่ายเป็นเสา $(L, \le)$ ซึ่งทุกคู่ $\lbrace a, b \rbrace \in L$ มีขอบเขตบนน้อยที่สุด (แสดงโดย $a \lor b$) และขอบเขตล่างที่ยิ่งใหญ่ที่สุด (แสดงโดย $a \land b$). LUB$(\lbrace a,b \rbrace)$เรียกว่าการรวมของ a และ b GLB$(\lbrace a,b \rbrace )$ เรียกว่าการพบกันของ a และ b
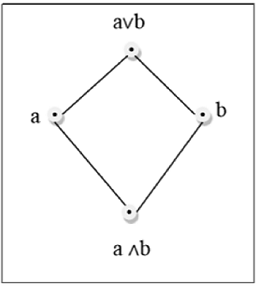
ตัวอย่าง
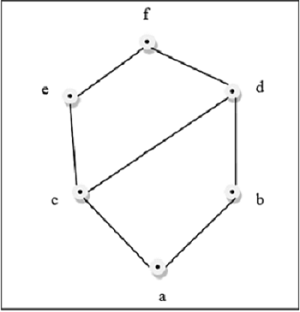
รูปด้านบนนี้เป็นโครงตาข่ายเพราะสำหรับทุกคู่ $\lbrace a, b \rbrace \in L$มี GLB และ LUB อยู่
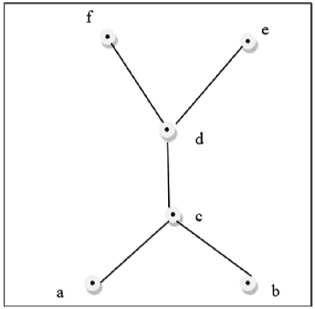
รูปด้านบนนี้ไม่ใช่โครงตาข่ายเพราะ $GLB (a, b)$ และ $LUB (e, f)$ ไม่ได้อยู่.
รายละเอียดอื่น ๆ มีการกล่าวถึงด้านล่าง -
ตาข่ายที่ถูกผูกไว้
ตาข่าย L จะกลายเป็นโครงตาข่ายที่มีขอบเขตถ้ามีองค์ประกอบที่ยิ่งใหญ่ที่สุด 1 และองค์ประกอบน้อยที่สุด 0
ตาข่ายเสริม
โครงตาข่าย L จะกลายเป็นโครงตาข่ายเสริมหากเป็นโครงตาข่ายที่มีขอบเขตและหากทุกองค์ประกอบในโครงตาข่ายมีส่วนประกอบ องค์ประกอบ x มีส่วนเติมเต็ม x 'if$\exists x(x \land x’=0 and x \lor x’ = 1)$
ตาข่ายกระจาย
ถ้าตาข่ายตรงตามคุณสมบัติการกระจายสองประการต่อไปนี้จะเรียกว่าตาข่ายการกระจาย
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
ตาข่ายโมดูลาร์
ถ้าตาข่ายตรงตามคุณสมบัติต่อไปนี้จะเรียกว่าตาข่ายแบบแยกส่วน
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
คุณสมบัติของคำโปรย
คุณสมบัติ Idempotent
$a \lor a = a$
$a \land a = a$
คุณสมบัติการดูดซึม
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
คุณสมบัติการสับเปลี่ยน
$a \lor b = b \lor a$
$a \land b = b \land a$
คุณสมบัติที่เกี่ยวข้อง
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
คู่ของ Lattice
คู่ของโครงตาข่ายได้มาจากการแลกเปลี่ยน '$\lor$'และ'$\land$'การดำเนินงาน.
ตัวอย่าง
คู่ของ $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$
ในชีวิตประจำวันหลายครั้งที่เราต้องการหาจำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมดสำหรับเหตุการณ์ต่างๆ ตัวอย่างเช่นสามารถเลือกคณะผู้พิพากษาที่ประกอบด้วยชาย 6 คนและหญิง 4 คนจากชาย 50 คนและหญิง 38 คนได้กี่วิธี สามารถสร้างตัวเลข PAN 10 ตัวอักษรที่แตกต่างกันได้กี่ตัวเพื่อให้ตัวอักษรห้าตัวแรกเป็นตัวพิมพ์ใหญ่สี่ตัวถัดไปเป็นตัวเลขและตัวสุดท้ายเป็นตัวพิมพ์ใหญ่อีกครั้ง สำหรับการแก้ปัญหาเหล่านี้จะใช้ทฤษฎีการนับทางคณิตศาสตร์Counting ส่วนใหญ่ครอบคลุมกฎการนับพื้นฐานกฎการเรียงสับเปลี่ยนและกฎการรวมกัน
กฎของผลรวมและผลิตภัณฑ์
Rule of Sum และ Rule of Product ใช้เพื่อแยกปัญหาการนับที่ยากให้กลายเป็นปัญหาง่ายๆ
The Rule of Sum - หากลำดับของงาน $T_1, T_2, \dots, T_m$ สามารถทำได้ใน $w_1, w_2, \dots w_m$ วิธีต่างๆตามลำดับ (เงื่อนไขคือไม่สามารถดำเนินการพร้อมกันได้) จำนวนวิธีในการทำงานอย่างใดอย่างหนึ่งเหล่านี้คือ $w_1 + w_2 + \dots +w_m$. ถ้าเราพิจารณาสองงาน A และ B ซึ่งไม่ปะติดปะต่อกัน (เช่น$A \cap B = \emptyset$) ตามด้วยคณิตศาสตร์ $|A \cup B| = |A| + |B|$
The Rule of Product - หากลำดับของงาน $T_1, T_2, \dots, T_m$ สามารถทำได้ใน $w_1, w_2, \dots w_m$ วิธีตามลำดับและทุกงานมาถึงหลังจากเกิดภารกิจก่อนหน้าแล้วก็มี $w_1 \times w_2 \times \dots \times w_m$วิธีการปฏิบัติงาน ในทางคณิตศาสตร์ถ้างาน B มาถึงหลังจากงาน A แล้ว$|A \times B| = |A|\times|B|$
ตัวอย่าง
Question- เด็กชายคนหนึ่งอาศัยอยู่ที่ X และต้องการไปโรงเรียนที่ Z จากบ้านของเขา X เขาต้องไปถึง Y ก่อนจากนั้น Y ไป Z เขาอาจไป X ถึง Y โดยรถประจำทาง 3 สายหรือ 2 เส้นทางรถไฟ จากนั้นเขาสามารถเลือกรถบัสได้ 4 เส้นทางหรือรถไฟ 5 เส้นทางเพื่อไปยัง Z มีวิธีการเดินทางจาก X ไป Z กี่วิธี?
Solution - จาก X ถึง Y เขาสามารถเข้าไปได้ $3 + 2 = 5$วิธี (กฎผลรวม) หลังจากนั้นเขาสามารถไป Y ถึง Z ได้$4 + 5 = 9$วิธี (กฎผลรวม) ดังนั้นจาก X ถึง Z เขาสามารถเข้าไปได้$5 \times 9 = 45$ วิธีการ (Rule of Product)
การเรียงสับเปลี่ยน
ก permutationเป็นการจัดเรียงองค์ประกอบบางอย่างที่ลำดับมีความสำคัญ กล่าวอีกนัยหนึ่งคือการเรียงสับเปลี่ยนเป็นการรวมองค์ประกอบตามลำดับ
ตัวอย่าง
จากชุด S = {x, y, z} โดยรับครั้งละสองชุดการเรียงสับเปลี่ยนทั้งหมดคือ -
$ xy, yx, xz, zx, yz, zy $.
เราต้องสร้างการเรียงสับเปลี่ยนของตัวเลขสามหลักจากชุดตัวเลข $S = \lbrace 1, 2, 3 \rbrace$. ตัวเลขสามหลักที่แตกต่างกันจะเกิดขึ้นเมื่อเราจัดเรียงตัวเลข การเรียงสับเปลี่ยนจะเป็น = 123, 132, 213, 231, 312, 321
จำนวนการเรียงลำดับ
จำนวนการเรียงสับเปลี่ยนของ 'n' สิ่งต่างๆที่นำมา 'r' ในแต่ละครั้งจะแสดงด้วย $n_{P_{r}}$
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
ที่ไหน $n! = 1.2.3. \dots (n - 1).n$
Proof - ให้มีองค์ประกอบที่แตกต่างกัน 'n'
มี n หลายวิธีในการเติมอันดับแรก หลังจากเติมองค์ประกอบที่หนึ่ง (n-1) แล้วจะเหลือจำนวนองค์ประกอบ ดังนั้นจึงมีวิธี (n-1) ในการเติมตำแหน่งที่สอง หลังจากเติมตำแหน่งที่หนึ่งและที่สองแล้วจะเหลือ (n-2) จำนวนองค์ประกอบ ดังนั้นจึงมี (n-2) วิธีในการเติมตำแหน่งที่สาม ตอนนี้เราสามารถสรุปหลายวิธีในการเติมตำแหน่ง r-th เป็น [n - (r – 1)] = n – r + 1
ดังนั้นจำนวนทั้งหมด วิธีการเติมจากที่หนึ่งถึง r-th-place -
$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$
$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$
ดังนั้น
$n_{ P_{ r } } = n! / (n-r)!$
สูตรที่สำคัญบางประการของการเปลี่ยนแปลง
หากมีองค์ประกอบnที่$a_1$ ก็เหมือนกัน $a_2$ มีลักษณะเหมือนกัน $a_3$ เป็นเหมือนประเภทที่สามและอื่น ๆ และ $a_r$ เป็นของ $r^{th}$ ชนิดที่ไหน $(a_1 + a_2 + ... a_r) = n$.
จากนั้นจำนวนการเรียงสับเปลี่ยนของวัตถุ n เหล่านี้คือ = $n! / [(a_1!(a_2!) \dots (a_r!)]$.
จำนวนการเรียงสับเปลี่ยนขององค์ประกอบที่แตกต่างกัน n การรับ n องค์ประกอบในแต่ละครั้ง = $n_{P_n} = n!$
จำนวนการเรียงสับเปลี่ยนขององค์ประกอบที่ไม่เหมือนกันที่รับองค์ประกอบ r ในแต่ละครั้งเมื่อ x สิ่งใดสิ่งหนึ่งครอบครองตำแหน่งที่แน่นอนเสมอ = $n-x_{p_{r-x}}$
จำนวนการเรียงสับเปลี่ยนของ n องค์ประกอบที่แตกต่างกันเมื่อ r สิ่งที่ระบุมารวมกันเสมอคือ - $r! (n−r+1)!$
จำนวนการเรียงสับเปลี่ยนของ n องค์ประกอบที่แตกต่างกันเมื่อ r สิ่งที่ระบุไม่เคยมารวมกันคือ - $n!–[r! (n−r+1)!]$
จำนวนการเรียงสับเปลี่ยนแบบวงกลมของ n องค์ประกอบที่แตกต่างกันที่ถ่าย x องค์ประกอบในเวลา = $^np_{x}/x$
จำนวนการเรียงสับเปลี่ยนแบบวงกลมของ n สิ่งต่างๆ = $^np_{n}/n$
ปัญหาบางอย่าง
Problem 1 - จากไพ่ 6 ใบที่แตกต่างกันเราจะอนุญาตมันได้กี่วิธี?
Solution - ในขณะที่เรารับไพ่ครั้งละ 6 ใบจากสำรับไพ่ 6 ใบการเรียงสับเปลี่ยนจะเป็น $^6P_{6} = 6! = 720$
Problem 2 - ตัวอักษรของคำว่า 'READER' สามารถจัดเรียงได้กี่วิธี?
Solution - มีตัวอักษร 6 คำ (2 E, 1 A, 1D และ 2R.) ในคำว่า 'READER'
การเปลี่ยนแปลงจะเป็น $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$
Problem 3 - วิธีการจัดเรียงตัวอักษรของคำว่า 'ORANGE' เพื่อให้พยัญชนะอยู่ในตำแหน่งคู่เท่านั้น?
Solution- มีสระ 3 ตัวและพยัญชนะ 3 ตัวในคำว่า 'ORANGE' จำนวนวิธีในการจัดเรียงพยัญชนะกันเอง$= ^3P_{3} = 3! = 6$. ตำแหน่งว่างที่เหลืออีก 3 แห่งจะถูกเติมด้วยเสียงสระ 3 ตัวใน$^3P_{3} = 3! = 6$วิธี ดังนั้นจำนวนการเปลี่ยนแปลงทั้งหมดคือ$6 \times 6 = 36$
ชุดค่าผสม
ก combination คือการเลือกองค์ประกอบที่กำหนดซึ่งลำดับไม่สำคัญ
จำนวนชุดค่าผสมทั้งหมดของ n สิ่งที่นำมาครั้งละ r คือ -
$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$
Problem 1
ค้นหาจำนวนชุดย่อยของชุด $\lbrace1, 2, 3, 4, 5, 6\rbrace$ มี 3 องค์ประกอบ
Solution
จำนวนสมาชิกของเซตคือ 6 และเราต้องเลือก 3 องค์ประกอบจากเซต ที่นี่การสั่งซื้อไม่สำคัญ ดังนั้นจำนวนส่วนย่อยจะเป็น$^6C_{3} = 20$.
Problem 2
มีผู้ชาย 6 คนและผู้หญิง 5 คนอยู่ในห้อง เราสามารถเลือกผู้ชาย 3 คนและผู้หญิง 2 คนจากห้องได้กี่วิธี?
Solution
จำนวนวิธีในการเลือกผู้ชาย 3 คนจากผู้ชาย 6 คนคือ $^6C_{3}$ และจำนวนวิธีในการเลือกผู้หญิง 2 คนจากผู้หญิง 5 คนคือ $^5C_{2}$
ดังนั้นจำนวนวิธีทั้งหมดคือ - $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$
Problem 3
คุณสามารถเลือกกลุ่มที่แตกต่างกัน 3 กลุ่มของนักเรียน 3 คนจากนักเรียนทั้งหมด 9 คนได้กี่วิธี?
Solution
ให้เรานับกลุ่มเป็น 1, 2 และ 3
สำหรับการเลือก 3 สำหรับนักเรียน 1 เซนต์กลุ่มจำนวนวิธีที่ -$^9C_{3}$
จำนวนของวิธีการเลือก 3 สำหรับนักเรียน 2 ครั้งกลุ่มหลังจากที่เลือกกลุ่มที่ 1 -$^6C_{3}$
จำนวนของวิธีการเลือก 3 สำหรับนักเรียน 3 ถกลุ่มหลังจากเลือก 1 เซนต์และ 2 ครั้งกลุ่ม -$^3C_{3}$
ดังนั้นจำนวนวิธีทั้งหมด $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$
เอกลักษณ์ของปาสคาล
ตัวตนของปาสคาลมาครั้งแรกโดย Blaise Pascal ใน 17 THศตวรรษที่ระบุว่าจำนวนของวิธีการที่จะเลือกองค์ประกอบ k จากองค์ประกอบ n มีค่าเท่ากับผลรวมของจำนวนของวิธีการที่จะเลือก (k-1) องค์ประกอบจาก (n-1) องค์ประกอบ และจำนวนวิธีในการเลือกองค์ประกอบจากองค์ประกอบ n-1
ทางคณิตศาสตร์สำหรับจำนวนเต็มบวก k และ n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$
Proof -
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$
$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$
$= (n-1)! \frac{ n } { k!(n-k)! }$
$= \frac{ n! } { k!(n-k)! }$
$= n_{ C_{ k } }$
หลักการ Pigeonhole
ในปีพ. ศ. 2377 ปีเตอร์กุสตาฟเลเจิร์นดิริชเล็ตนักคณิตศาสตร์ชาวเยอรมันได้กล่าวถึงหลักการที่เขาเรียกว่าหลักการลิ้นชัก ตอนนี้เรียกได้ว่าเป็นหลักการของนกพิราบ
Pigeonhole Principleระบุว่าหากมีรูของนกพิราบน้อยกว่าจำนวนนกพิราบทั้งหมดและนกพิราบแต่ละตัวถูกใส่ไว้ในหลุมของนกพิราบจะต้องมีหลุมนกพิราบอย่างน้อยหนึ่งหลุมที่มีนกพิราบมากกว่าหนึ่งตัว ถ้าใส่นกพิราบ n เข้าไปใน m pigeonholes โดยที่ n> m มีรูที่มีนกพิราบมากกว่าหนึ่งตัว
ตัวอย่าง
มีผู้ชายสิบคนอยู่ในห้องและพวกเขามีส่วนร่วมในการจับมือกัน หากแต่ละคนจับมือกันอย่างน้อยหนึ่งครั้งและไม่มีผู้ชายคนใดจับมือของชายคนเดียวกันมากกว่าหนึ่งครั้งแสดงว่ามีผู้ชายสองคนเข้าร่วมในจำนวนการจับมือเดียวกัน
ต้องมีอย่างน้อยสองคนในคลาส 30 คนที่ชื่อขึ้นต้นด้วยตัวอักษรเดียวกัน
หลักการรวม - การยกเว้น
Inclusion-exclusion principleคำนวณจำนวนที่สำคัญของการรวมกันของชุดที่ไม่ปะติดปะต่อกันหลายชุด สำหรับสองชุด A และ B หลักการระบุ -
$|A \cup B| = |A| + |B| - |A \cap B|$
สำหรับสามชุด A, B และ C หลักการระบุ -
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
สูตรทั่วไป -
$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$
Problem 1
จำนวนเต็ม 1 ถึง 50 เป็นจำนวนเต็มของ 2 หรือ 3 แต่ไม่ใช่ทั้งสองจำนวน
Solution
ตั้งแต่ 1 ถึง 100 มี $50/2 = 25$ ตัวเลขซึ่งเป็นทวีคูณของ 2
มี $50/3 = 16$ ตัวเลขซึ่งเป็นทวีคูณของ 3
มี $50/6 = 8$ ตัวเลขซึ่งเป็นทวีคูณของทั้ง 2 และ 3
ดังนั้น, $|A|=25$, $|B|=16$ และ $|A \cap B|= 8$.
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
Problem 2
ในกลุ่มนักเรียน 50 คน 24 คนชอบเครื่องดื่มเย็น ๆ และชอบดื่มร้อน 36 คนและนักเรียนแต่ละคนชอบเครื่องดื่มอย่างน้อยหนึ่งในสองแก้ว หลายคนชอบทั้งกาแฟและชา?
Solution
ให้ X เป็นชุดของนักเรียนที่ชอบเครื่องดื่มเย็นและ Y เป็นชุดของคนที่ชอบเครื่องดื่มร้อน
ดังนั้น, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$
ดังนั้นจึงมีนักเรียน 10 คนที่ชอบทั้งชาและกาแฟ
ที่เกี่ยวข้องอย่างใกล้ชิดกับแนวคิดของการนับคือความน่าจะเป็น เรามักจะพยายามเดาผลลัพธ์ของเกมแห่งโอกาสเช่นเกมไพ่สล็อตแมชชีนและลอตเตอรี่ กล่าวคือเราพยายามค้นหาความเป็นไปได้หรือความน่าจะเป็นที่จะได้ผลลัพธ์ที่เฉพาะเจาะจง
Probabilityสามารถกำหนดแนวความคิดได้ว่าเป็นการหาโอกาสที่จะเกิดเหตุการณ์ ในทางคณิตศาสตร์เป็นการศึกษากระบวนการสุ่มและผลลัพธ์ของมัน กฎแห่งความน่าจะเป็นมีผลบังคับใช้อย่างกว้างขวางในหลากหลายสาขาเช่นพันธุศาสตร์การพยากรณ์อากาศการสำรวจความคิดเห็นตลาดหุ้นเป็นต้น
แนวคิดพื้นฐาน
ทฤษฎีความน่าจะเป็นถูกคิดค้นขึ้นในศตวรรษที่ 17 โดยนักคณิตศาสตร์ชาวฝรั่งเศสสองคนคือเบลสปาสคาลและปิแอร์เดอแฟร์มาต์ซึ่งกำลังจัดการกับปัญหาทางคณิตศาสตร์เกี่ยวกับโอกาส
ก่อนที่จะดำเนินการต่อในรายละเอียดของความน่าจะเป็นให้เราเข้าใจแนวคิดของคำจำกัดความบางอย่าง
Random Experiment- การทดลองที่ทราบผลลัพธ์ที่เป็นไปได้ทั้งหมดและไม่สามารถคาดการณ์ผลลัพธ์ที่แน่นอนได้ล่วงหน้าเรียกว่าการทดลองแบบสุ่ม การโยนเหรียญยุติธรรมเป็นตัวอย่างของการทดลองแบบสุ่ม
Sample Space- เมื่อเราทำการทดลองชุด S ของผลลัพธ์ที่เป็นไปได้ทั้งหมดจะเรียกว่าพื้นที่ตัวอย่าง ถ้าเราโยนเหรียญช่องว่างตัวอย่าง$S = \left \{ H, T \right \}$
Event- ส่วนย่อยของพื้นที่ตัวอย่างใด ๆ เรียกว่าเหตุการณ์ หลังจากโยนเหรียญแล้วการที่ Head อยู่ด้านบนคือเหตุการณ์
คำว่า "ความน่าจะเป็น" หมายถึงโอกาสที่จะเกิดเหตุการณ์ใดเหตุการณ์หนึ่ง สิ่งที่ดีที่สุดที่เราสามารถพูดได้คือความเป็นไปได้ที่จะเกิดขึ้นโดยใช้แนวคิดเรื่องความน่าจะเป็น
$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$
เนื่องจากการเกิดเหตุการณ์ใด ๆ แตกต่างกันไประหว่าง 0% ถึง 100% ความน่าจะเป็นจึงแตกต่างกันไประหว่าง 0 ถึง 1
ขั้นตอนในการค้นหาความน่าจะเป็น
ขั้นตอนที่ 1 - คำนวณผลลัพธ์ที่เป็นไปได้ทั้งหมดของการทดสอบ
ขั้นตอนที่ 2 - คำนวณจำนวนผลลัพธ์ที่ดีของการทดสอบ
ขั้นตอนที่ 3 - ใช้สูตรความน่าจะเป็นที่สอดคล้องกัน
การโยนเหรียญ
หากมีการโยนเหรียญมีสองผลลัพธ์ที่เป็นไปได้ - หัว $(H)$ หรือหาง $(T)$
ดังนั้นจำนวนผลลัพธ์ทั้งหมด = 2
ดังนั้นความน่าจะเป็นที่จะได้หัวหน้า $(H)$ ด้านบนคือ 1/2 และความน่าจะเป็นที่จะได้ก้อย $(T)$ ด้านบนคือ 1/2
ทอยลูกเต๋า
เมื่อทอยลูกเต๋าผลลัพธ์ที่เป็นไปได้หกประการจะอยู่ด้านบน - $1, 2, 3, 4, 5, 6$.
ความน่าจะเป็นของตัวเลขใดตัวหนึ่งคือ 1/6
ความน่าจะเป็นที่จะได้เลขคู่คือ 3/6 = 1/2
ความน่าจะเป็นที่จะได้เลขคี่คือ 3/6 = 1/2
รับการ์ดจากเด็ค
จากสำรับไพ่ 52 ใบหากหยิบไพ่หนึ่งใบให้ค้นหาความน่าจะเป็นที่เอซจะถูกดึงออกมาและค้นหาความน่าจะเป็นของการดึงเพชร
จำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมด - 52
ผลลัพธ์ของการเป็นเอซ - 4
ความน่าจะเป็นของการเป็นเอซ = 4/52 = 1/13
ความน่าจะเป็นเพชร = 13/52 = 1/4
สัจพจน์ของความน่าจะเป็น
ความน่าจะเป็นของเหตุการณ์จะแตกต่างกันไปตั้งแต่ 0 ถึง 1 เสมอ $[0 \leq P(x) \leq 1]$
สำหรับเหตุการณ์ที่เป็นไปไม่ได้ความน่าจะเป็นคือ 0 และสำหรับเหตุการณ์หนึ่งความน่าจะเป็นคือ 1
หากการเกิดขึ้นของเหตุการณ์หนึ่งไม่ได้รับอิทธิพลจากเหตุการณ์อื่นพวกเขาจะเรียกว่าเหตุการณ์พิเศษซึ่งกันและกันหรือไม่ปะติดปะต่อกัน
ถ้า $A_1, A_2....A_n$ เป็นเหตุการณ์พิเศษ / ไม่ปะติดปะต่อกันจากนั้น $P(A_i \cap A_j) = \emptyset $ สำหรับ $i \ne j$ และ $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
คุณสมบัติของความน่าจะเป็น
หากมีสองเหตุการณ์ $x$ และ $\overline{x}$ซึ่งเป็นส่วนเสริมความน่าจะเป็นของเหตุการณ์เสริมคือ -
$$p(\overline{x}) = 1-p(x)$$
สำหรับสองเหตุการณ์ที่ไม่ปะติดปะต่อ A และ B ความน่าจะเป็นของการรวมกันของสองเหตุการณ์ -
$P(A \cup B) = P(A) + P(B)$
ถ้าเหตุการณ์ A เป็นส่วนย่อยของเหตุการณ์อื่น B (เช่น $A \subset B$) ดังนั้นความน่าจะเป็นของ A จะน้อยกว่าหรือเท่ากับความน่าจะเป็นของ B ดังนั้น $A \subset B$ หมายถึง $P(A) \leq p(B)$
ความน่าจะเป็นตามเงื่อนไข
ความน่าจะเป็นตามเงื่อนไขของเหตุการณ์ B คือความน่าจะเป็นที่เหตุการณ์จะเกิดขึ้นเนื่องจากเหตุการณ์ A ได้เกิดขึ้นแล้ว สิ่งนี้เขียนเป็น$P(B|A)$.
ทางคณิตศาสตร์ - $ P(B|A) = P(A \cap B)/ P(A)$
หากเหตุการณ์ A และ B ไม่รวมกันดังนั้นความน่าจะเป็นตามเงื่อนไขของเหตุการณ์ B หลังจากเหตุการณ์ A จะเป็นความน่าจะเป็นของเหตุการณ์ B ที่เป็น $P(B)$.
Problem 1
ในประเทศหนึ่ง ๆ 50% ของวัยรุ่นทั้งหมดเป็นเจ้าของจักรยานและ 30% ของวัยรุ่นทั้งหมดเป็นเจ้าของจักรยานและจักรยาน ความน่าจะเป็นที่วัยรุ่นเป็นเจ้าของจักรยานคืออะไรเนื่องจากวัยรุ่นเป็นเจ้าของวงจร?
Solution
สมมติว่า A คือเหตุการณ์ของวัยรุ่นที่เป็นเจ้าของจักรยานเท่านั้นและ B คือเหตุการณ์ของวัยรุ่นที่มีจักรยานเท่านั้น
ดังนั้น, $P(A) = 50/100 = 0.5$ และ $P(A \cap B) = 30/100 = 0.3$ จากปัญหาที่กำหนด
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
ดังนั้นความน่าจะเป็นที่วัยรุ่นเป็นเจ้าของจักรยานเนื่องจากวัยรุ่นเป็นเจ้าของวงจรคือ 60%
Problem 2
ในชั้นเรียน 50% ของนักเรียนทั้งหมดเล่นคริกเก็ตและ 25% ของนักเรียนทั้งหมดเล่นคริกเก็ตและวอลเลย์บอล ความน่าจะเป็นที่นักเรียนเล่นวอลเลย์บอลคืออะไรเนื่องจากนักเรียนเล่นคริกเก็ต
Solution
สมมติว่า A คือเหตุการณ์ของนักเรียนที่เล่นคริกเก็ตเท่านั้นและ B คือเหตุการณ์ของนักเรียนที่เล่นวอลเลย์บอลเท่านั้น
ดังนั้น, $P(A) = 50/100 =0.5$ และ $P(A \cap B) = 25/ 100 =0.25$ จากปัญหาที่กำหนด
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
ดังนั้นความน่าจะเป็นที่นักเรียนเล่นวอลเลย์บอลเนื่องจากนักเรียนเล่นคริกเก็ตคือ 50%
Problem 3
แล็ปท็อปที่ดีหกเครื่องและแล็ปท็อปที่มีข้อบกพร่องสามเครื่องผสมกัน หากต้องการค้นหาแล็ปท็อปที่มีข้อบกพร่องทั้งหมดจะได้รับการทดสอบแบบสุ่มทีละเครื่อง ความเป็นไปได้ที่จะพบแล็ปท็อปทั้งสองเครื่องที่มีข้อบกพร่องในการเลือกสองครั้งแรกเป็นอย่างไร
Solution
ให้ A เป็นเหตุการณ์ที่เราพบแล็ปท็อปที่มีข้อบกพร่องในการทดสอบครั้งแรกและ B เป็นเหตุการณ์ที่เราพบแล็ปท็อปที่มีข้อบกพร่องในการทดสอบครั้งที่สอง
ดังนั้น $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
ทฤษฎีบทของ Bayes
Theorem - ถ้า A และ B เป็นสองเหตุการณ์พิเศษโดยที่ $P(A)$ คือความน่าจะเป็นของ A และ $P(B)$ คือความน่าจะเป็นของ B $P(A | B)$ คือความน่าจะเป็นของ A ที่ระบุว่า B เป็นจริง $P(B | A)$ คือความน่าจะเป็นของ B เมื่อพิจารณาว่า A เป็นจริงแล้วสถานะของทฤษฎีบทของเบย์ -
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
การประยุกต์ใช้ทฤษฎีบทของเบย์
ในสถานการณ์ที่เหตุการณ์ทั้งหมดของพื้นที่ตัวอย่างเป็นเหตุการณ์พิเศษซึ่งกันและกัน
ในสถานการณ์ที่อย่างใดอย่างหนึ่ง $P( A_i \cap B )$ แต่ละ $A_i$ หรือ $P( A_i )$ และ $P(B|A_i)$ แต่ละ $A_i$ เป็นที่รู้จัก
Problem
พิจารณาสามปากกา แท่นวางปากการุ่นแรกประกอบด้วยปากกาสีแดง 2 ด้ามและปากกาสีน้ำเงิน 3 ด้าม อันที่สองมีปากกาสีแดง 3 ด้ามและปากกาสีน้ำเงิน 2 ด้าม ส่วนอันที่สามมีปากกาสีแดง 4 ด้ามและปากกาสีน้ำเงิน 1 ด้าม มีความเป็นไปได้ที่จะเลือกแท่นวางปากกาแต่ละอันเท่ากัน หากสุ่มจับปากกาหนึ่งด้ามความน่าจะเป็นที่จะเป็นปากกาสีแดงคืออะไร?
Solution
ปล่อย $A_i$เป็นเหตุการณ์ที่ฉันTHปากกายืนถูกเลือก
ที่นี่ผม = 1,2,3
เนื่องจากความน่าจะเป็นในการเลือกแท่นวางปากกามีค่าเท่ากัน $P(A_i) = 1/3$
ให้ B เป็นฝ่ายจับปากกาสีแดง
ความเป็นไปได้ที่จะมีการเลือกปากกาสีแดงในห้าปากกาของแท่นวางปากกาตัวแรก
$P(B|A_1) = 2/5$
ความน่าจะเป็นที่ปากกาสีแดงถูกเลือกระหว่างปากกาห้าด้ามของแท่นวางปากกาที่สอง
$P(B|A_2) = 3/5$
ความน่าจะเป็นที่ปากกาสีแดงถูกเลือกจากปากกาห้าด้ามของแท่นวางปากกาที่สาม
$P(B|A_3) = 4/5$
ตามทฤษฎีบทของ Bayes
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
Mathematical inductionเป็นเทคนิคในการพิสูจน์ผลลัพธ์หรือสร้างข้อความสำหรับจำนวนธรรมชาติ ส่วนนี้จะแสดงวิธีการผ่านตัวอย่างต่างๆ
คำจำกัดความ
Mathematical Induction เป็นเทคนิคทางคณิตศาสตร์ที่ใช้ในการพิสูจน์คำสั่งสูตรหรือทฤษฎีบทเป็นจริงสำหรับจำนวนธรรมชาติทุกตัว
เทคนิคนี้เกี่ยวข้องกับสองขั้นตอนในการพิสูจน์คำแถลงดังที่ระบุไว้ด้านล่าง -
Step 1(Base step) - พิสูจน์ได้ว่าคำสั่งนั้นเป็นจริงสำหรับค่าเริ่มต้น
Step 2(Inductive step)- มันพิสูจน์ให้เห็นว่าถ้าคำสั่งที่เป็นจริงสำหรับเอ็นTHซ้ำ (หรือจำนวนn ) แล้วมันยังเป็นจริงสำหรับ(n + 1) THซ้ำ (หรือหมายเลข1 + n )
ทำอย่างไร
Step 1- พิจารณาค่าเริ่มต้นที่ข้อความนั้นเป็นจริง จะต้องแสดงให้เห็นว่าคำสั่งเป็นจริงสำหรับ n = ค่าเริ่มต้น
Step 2- สมมติคำสั่งที่เป็นจริงสำหรับค่าของn = k แล้วพิสูจน์คำสั่งที่เป็นจริงสำหรับn = k + 1 เราแบ่งn = k + 1ออกเป็นสองส่วนส่วนหนึ่งคือn = k (ซึ่งพิสูจน์แล้ว) และพยายามพิสูจน์อีกส่วนหนึ่ง
ปัญหา 1
$3^n-1$ คือผลคูณของ 2 สำหรับ n = 1, 2, ...
Solution
Step 1 - สำหรับ $n = 1, 3^1-1 = 3-1 = 2$ ซึ่งเป็นผลคูณของ 2
Step 2 - ให้เราสมมติ $3^n-1$ เป็นจริงสำหรับ $n=k$, ดังนั้น $3^k -1$ เป็นความจริง (เป็นข้อสันนิษฐาน)
เราต้องพิสูจน์สิ่งนั้น $3^{k+1}-1$ ยังเป็นผลคูณของ 2
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
ส่วนแรก $(2 \times 3k)$ แน่นอนว่าเป็นผลคูณของ 2 และส่วนที่สอง $(3k -1)$ is also true as our previous assumption.
Hence, $3^{k+1} – 1$ is a multiple of 2.
So, it is proved that $3^n – 1$ is a multiple of 2.
Problem 2
$1 + 3 + 5 + ... + (2n-1) = n^2$ for $n = 1, 2, \dots $
Solution
Step 1 − For $n=1, 1 = 1^2$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$.
Hence, $1 + 3 + 5 + \dots + (2k-1) = k^2$ is true (It is an assumption)
We have to prove that $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ also holds
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
So, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ hold which satisfies the step 2.
Hence, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ is proved.
Problem 3
Prove that $(ab)^n = a^nb^n$ is true for every natural number $n$
Solution
Step 1 − For $n=1, (ab)^1 = a^1b^1 = ab$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$, Hence, $(ab)^k = a^kb^k$ is true (It is an assumption).
We have to prove that $(ab)^{k+1} = a^{k+1}b^{k+1}$ also hold
Given, $(ab)^k = a^k b^k$
Or, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Multiplying both side by 'ab']
Or, $(ab)^{k+1} = (aa^k) ( bb^k)$
Or, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
Hence, step 2 is proved.
So, $(ab)^n = a^nb^n$ is true for every natural number n.
Strong Induction
Strong Induction is another form of mathematical induction. Through this induction technique, we can prove that a propositional function, $P(n)$ is true for all positive integers, $n$, using the following steps −
Step 1(Base step) − It proves that the initial proposition $P(1)$ true.
Step 2(Inductive step) − It proves that the conditional statement $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ is true for positive integers $k$.
In this chapter, we will discuss how recursive techniques can derive sequences and be used for solving counting problems. The procedure for finding the terms of a sequence in a recursive manner is called recurrence relation. We study the theory of linear recurrence relations and their solutions. Finally, we introduce generating functions for solving recurrence relations.
Definition
A recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing $F_n$ as some combination of $F_i$ with $i < n$).
Example − Fibonacci series − $F_n = F_{n-1} + F_{n-2}$, Tower of Hanoi − $F_n = 2F_{n-1} + 1$
Linear Recurrence Relations
A linear recurrence equation of degree k or order k is a recurrence equation which is in the format $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ is a constant and $A_k \neq 0$) on a sequence of numbers as a first-degree polynomial.
These are some examples of linear recurrence equations −
| Recurrence relations | Initial values | Solutions |
|---|---|---|
| Fn = Fn-1 + Fn-2 | a1 = a2 = 1 | Fibonacci number |
| Fn = Fn-1 + Fn-2 | a1 = 1, a2 = 3 | Lucas Number |
| Fn = Fn-2 + Fn-3 | a1 = a2 = a3 = 1 | Padovan sequence |
| Fn = 2Fn-1 + Fn-2 | a1 = 0, a2 = 1 | Pell number |
How to solve linear recurrence relation
Suppose, a two ordered linear recurrence relation is − $F_n = AF_{n-1} +BF_{n-2}$ where A and B are real numbers.
The characteristic equation for the above recurrence relation is −
$$x^2 - Ax - B = 0$$
Three cases may occur while finding the roots −
Case 1 − If this equation factors as $(x- x_1)(x- x_1) = 0$ and it produces two distinct real roots $x_1$ and $x_2$, then $F_n = ax_1^n+ bx_2^n$ is the solution. [Here, a and b are constants]
Case 2 − If this equation factors as $(x- x_1)^2 = 0$ and it produces single real root $x_1$, then $F_n = a x_1^n+ bn x_1^n$ is the solution.
Case 3 − If the equation produces two distinct complex roots, $x_1$ and $x_2$ in polar form $x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta)$, then $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ is the solution.
Problem 1
Solve the recurrence relation $F_n = 5F_{n-1} - 6F_{n-2}$ where $F_0 = 1$ and $F_1 = 4$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 - 5x + 6 = 0,$$
So, $(x - 3) (x - 2) = 0$
Hence, the roots are −
$x_1 = 3$ and $x_2 = 2$
The roots are real and distinct. So, this is in the form of case 1
Hence, the solution is −
$$F_n = ax_1^n + bx_2^n$$
Here, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$
Therefore,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
Solving these two equations, we get $ a = 2$ and $b = -1$
Hence, the final solution is −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
Problem 2
Solve the recurrence relation − $F_n = 10F_{n-1} - 25F_{n-2}$ where $F_0 = 3$ and $F_1 = 17$
Solution
The characteristic equation of the recurrence relation is −
$$ x^2 - 10x -25 = 0$$
So $(x - 5)^2 = 0$
Hence, there is single real root $x_1 = 5$
As there is single real valued root, this is in the form of case 2
Hence, the solution is −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
Solving these two equations, we get $a = 3$ and $b = 2/5$
Hence, the final solution is − $F_n = 3.5^n +( 2/5) .n.2^n $
Problem 3
Solve the recurrence relation $F_n = 2F_{n-1} - 2F_{n-2}$ where $F_0 = 1$ and $F_1 = 3$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 -2x -2 = 0$$
Hence, the roots are −
$x_1 = 1 + i$ and $x_2 = 1 - i$
In polar form,
$x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta),$ where $r = \sqrt 2$ and $\theta = \frac{\pi}{4}$
The roots are imaginary. So, this is in the form of case 3.
Hence, the solution is −
$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
Solving these two equations we get $a = 1$ and $b = 2$
Hence, the final solution is −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
Non-Homogeneous Recurrence Relation and Particular Solutions
A recurrence relation is called non-homogeneous if it is in the form
$F_n = AF_{n-1} + BF_{n-2} + f(n)$ where $f(n) \ne 0$
Its associated homogeneous recurrence relation is $F_n = AF_{n–1} + BF_{n-2}$
The solution $(a_n)$ of a non-homogeneous recurrence relation has two parts.
First part is the solution $(a_h)$ of the associated homogeneous recurrence relation and the second part is the particular solution $(a_t)$.
$$a_n=a_h+a_t$$
Solution to the first part is done using the procedures discussed in the previous section.
To find the particular solution, we find an appropriate trial solution.
Let $f(n) = cx^n$ ; let $x^2 = Ax + B$ be the characteristic equation of the associated homogeneous recurrence relation and let $x_1$ and $x_2$ be its roots.
If $x \ne x_1$ and $x \ne x_2$, then $a_t = Ax^n$
If $x = x_1$, $x \ne x_2$, then $a_t = Anx^n$
If $x = x_1 = x_2$, then $a_t = An^2x^n$
Example
Let a non-homogeneous recurrence relation be $F_n = AF_{n–1} + BF_{n-2} + f(n)$ with characteristic roots $x_1 = 2$ and $x_2 = 5$. Trial solutions for different possible values of $f(n)$ are as follows −