คณิตศาสตร์ไม่ต่อเนื่อง - เซต

นักคณิตศาสตร์ชาวเยอรมัน G. Cantorแนะนำแนวคิดของชุด เขาได้กำหนดชุดให้เป็นชุดของวัตถุที่ชัดเจนและแยกแยะได้ซึ่งเลือกโดยกฎหรือคำอธิบายบางอย่าง

Setทฤษฎีเป็นพื้นฐานของการศึกษาสาขาอื่น ๆ เช่นทฤษฎีการนับความสัมพันธ์ทฤษฎีกราฟและเครื่องกำหนดสถานะ จำกัด ในบทนี้เราจะกล่าวถึงแง่มุมต่างๆของSet Theory.

ชุด - คำจำกัดความ

ชุดคือคอลเลกชันที่ไม่เรียงลำดับขององค์ประกอบต่างๆ ชุดสามารถเขียนอย่างชัดเจนโดยการระบุองค์ประกอบโดยใช้วงเล็บชุด หากลำดับขององค์ประกอบมีการเปลี่ยนแปลงหรือมีการทำซ้ำองค์ประกอบใด ๆ ของชุดจะไม่ทำการเปลี่ยนแปลงใด ๆ ในชุด

ตัวอย่างบางส่วนของชุด

ชุดของจำนวนเต็มบวกทั้งหมด
ชุดของดาวเคราะห์ทั้งหมดในระบบสุริยะ
ชุดของรัฐทั้งหมดในอินเดีย
ชุดตัวอักษรพิมพ์เล็กทั้งหมดของตัวอักษร

การเป็นตัวแทนของชุด

ชุดสามารถแสดงได้สองวิธี -

บัญชีรายชื่อหรือรูปแบบตาราง
ตั้งค่าสัญกรณ์ตัวสร้าง

บัญชีรายชื่อหรือรูปแบบตาราง

ชุดนี้แสดงโดยการแสดงรายการองค์ประกอบทั้งหมดที่ประกอบด้วยชุดนั้น องค์ประกอบจะอยู่ภายในวงเล็บปีกกาและคั่นด้วยเครื่องหมายจุลภาค

Example 1 - ชุดสระในตัวอักษรภาษาอังกฤษ $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 - ชุดเลขคี่น้อยกว่า 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

ตั้งค่าสัญกรณ์ตัวสร้าง

ชุดนี้กำหนดโดยการระบุคุณสมบัติที่องค์ประกอบของชุดมีเหมือนกัน ชุดนี้อธิบายว่า $ A = \ lbrace x: p (x) \ rbrace $

Example 1 - ชุด $ \ lbrace a, e, i, o, u \ rbrace $ เขียนเป็น -

$ A = \ lbrace x: \ text {x เป็นสระในตัวอักษรภาษาอังกฤษ} \ rbrace $

Example 2 - ชุด $ \ lbrace 1,3,5,7,9 \ rbrace $ เขียนเป็น -

$ B = \ lbrace x: 1 \ le x \ lt 10 \ และ \ (x \% 2) \ ne 0 \ rbrace $

หากองค์ประกอบ x เป็นสมาชิกของชุด S ใด ๆ จะแสดงด้วย $ x \ ใน S $ และถ้าองค์ประกอบ y ไม่ใช่สมาชิกของชุด S องค์ประกอบนั้นจะแสดงด้วย $ y \ not ใน S $

Example- ถ้า $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ ใน S $ แต่ $ 1.5 \ notin S $

ชุดที่สำคัญบางอย่าง

N - เซตของจำนวนธรรมชาติทั้งหมด = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z - เซตของจำนวนเต็มทั้งหมด = $ \ lbrace ..... , -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ - เซตของจำนวนเต็มบวกทั้งหมด

Q - ชุดของตัวเลขที่มีเหตุผลทั้งหมด

R - ชุดของจำนวนจริงทั้งหมด

W - ชุดของจำนวนเต็มทั้งหมด

Cardinality ของชุด

จำนวนองค์ประกอบของเซต S แสดงด้วย $ | S | $ คือจำนวนองค์ประกอบของเซต หมายเลขนี้เรียกอีกอย่างว่าหมายเลขคาร์ดินัล หากชุดมีจำนวนองค์ประกอบไม่ จำกัด จำนวนความสำคัญของมันคือ $ \ infty $

Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $

หากมีสองชุด X และ Y

$ | X | = | Y | $ หมายถึงสองชุด X และ Y ที่มีความสำคัญเท่ากัน เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X เท่ากับจำนวนองค์ประกอบใน Y ในกรณีนี้มีฟังก์ชัน bijective 'f' จาก X ถึง Y
$ | X | \ le | Y | $ หมายถึงว่าเซตคาร์ดินาลลิตี้ของ X น้อยกว่าหรือเท่ากับเซ็ตคาร์ดินาลลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่าหรือเท่ากับ Y ที่นี่มีฟังก์ชันฉีด 'f' จาก X ถึง Y
$ | X | \ lt | Y | $ หมายถึงว่าเซ็ตคาร์ดินาลลิตี้ของ X น้อยกว่าเซ็ตคาร์ดินาลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่า Y ในที่นี้ฟังก์ชัน 'f' จาก X ถึง Y เป็นฟังก์ชันแบบฉีด แต่ไม่ได้เป็น bijective
$ ถ้า \ | X | \ le | Y | $ และ $ | X | \ ge | Y | $ แล้ว $ | X | = | Y | $. ชุด X และ Y มักเรียกกันว่าเซตที่เท่ากัน

ประเภทของชุด

ชุดสามารถแบ่งออกเป็นหลายประเภท บางส่วนเป็นแบบ จำกัด ไม่สิ้นสุดเซตย่อยสากลเหมาะสมชุดซิงเกิลตัน ฯลฯ

ชุดไฟไนต์

ชุดที่มีจำนวนองค์ประกอบที่แน่นอนเรียกว่าเซต จำกัด

Example- $ S = \ lbrace x \: | \: x \ ใน N $ และ $ 70 \ gt x \ gt 50 \ rbrace $

ชุดไม่มีที่สิ้นสุด

ชุดที่มีองค์ประกอบจำนวนไม่ จำกัด เรียกว่าเซตไม่มีที่สิ้นสุด

Example- $ S = \ lbrace x \: | \: x \ ใน N $ และ $ x \ gt 10 \ rbrace $

ชุดย่อย

เซต X เป็นเซตย่อยของเซต Y (เขียนเป็น $ X \ subseteq Y $) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y

Example 1- ให้ $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ และ $ Y = \ lbrace 1, 2 \ rbrace $ ที่นี่เซ็ต Y เป็นเซตย่อยของเซต X เนื่องจากองค์ประกอบทั้งหมดของเซต Y อยู่ในเซต X ดังนั้นเราสามารถเขียน $ Y \ subseteq X $ ได้

Example 2- ให้ $ X = \ lbrace 1, 2, 3 \ rbrace $ และ $ Y = \ lbrace 1, 2, 3 \ rbrace $ ชุด Y เป็นส่วนย่อย (ไม่ใช่ชุดย่อยที่เหมาะสม) ของชุด X เนื่องจากองค์ประกอบทั้งหมดของชุด Y อยู่ในชุด X ดังนั้นเราสามารถเขียน $ Y \ subseteq X $ ได้

ชุดย่อยที่เหมาะสม

คำว่า "ชุดย่อยที่เหมาะสม" สามารถกำหนดเป็น "ชุดย่อย แต่ไม่เท่ากับ" เซต X เป็นเซตย่อยที่เหมาะสมของเซต Y (เขียนเป็น $ X \ เซตย่อย Y $) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y และ $ | X | \ lt | Y | $.

Example- ให้ $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ และ $ Y = \ lbrace 1, 2 \ rbrace $ ที่นี่ตั้งค่า $ Y \ subset X $ เนื่องจากองค์ประกอบทั้งหมดใน $ Y $ มีอยู่ใน $ X $ ด้วยและ $ X $ ก็มีอย่างน้อยหนึ่งองค์ประกอบที่มากกว่าตั้ง $ Y $

ชุดสากล

เป็นการรวบรวมองค์ประกอบทั้งหมดในบริบทหรือแอปพลิเคชันเฉพาะ ชุดทั้งหมดในบริบทหรือแอปพลิเคชันนั้นเป็นส่วนย่อยของชุดสากลนี้ ชุดสากลจะแสดงเป็น $ U $

Example- เราอาจกำหนด $ U $ เป็นชุดของสัตว์ทั้งหมดบนโลก ในกรณีนี้ชุดของสัตว์เลี้ยงลูกด้วยนมทั้งหมดเป็นชุดย่อยของ $ U $ ชุดของปลาทั้งหมดเป็นชุดย่อยของ $ U $ ชุดของแมลงทั้งหมดเป็นชุดย่อยของ $ U $ และอื่น ๆ

ชุดว่างหรือชุดค่าว่าง

ชุดว่างไม่มีองค์ประกอบ แสดงโดย $ \ emptyset $ เนื่องจากจำนวนองค์ประกอบในเซตว่างมีจำนวน จำกัด เซตว่างจึงเป็นเซต จำกัด จำนวนเต็มของเซตว่างหรือเซตว่างเป็นศูนย์

Example- $ S = \ lbrace x \: | \: x \ ใน N $ และ $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

Singleton Set หรือ Unit Set

ชุด Singleton หรือชุดหน่วยประกอบด้วยองค์ประกอบเดียว ชุดซิงเกิลตันแสดงด้วย $ \ lbrace s \ rbrace $

Example- $ S = \ lbrace x \: | \: x \ ใน N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

ชุดที่เท่ากัน

ถ้าสองชุดมีองค์ประกอบเดียวกันก็จะถือว่าเท่ากัน

Example - ถ้า $ A = \ lbrace 1, 2, 6 \ rbrace $ และ $ B = \ lbrace 6, 1, 2 \ rbrace $ ค่าเหล่านี้จะมีค่าเท่ากันทุกองค์ประกอบของเซต A คือองค์ประกอบของเซต B และทุกองค์ประกอบของเซต B เป็นองค์ประกอบของเซต A

ชุดที่เทียบเท่า

ถ้าความสำคัญของสองชุดเหมือนกันจะเรียกว่าชุดที่เท่ากัน

Example- ถ้า $ A = \ lbrace 1, 2, 6 \ rbrace $ และ $ B = \ lbrace 16, 17, 22 \ rbrace $ ค่าเหล่านี้จะเทียบเท่ากับคาร์ดินาลิตี้ของ A เท่ากับคาร์ดินาลลิตี้ของ B เช่น $ | A | = | B | = 3 $

ชุดที่ทับซ้อนกัน

สองชุดที่มีองค์ประกอบร่วมอย่างน้อยหนึ่งชุดเรียกว่าชุดที่ทับซ้อนกัน

กรณีชุดทับ -

$ n (A \ cup B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $

Example- ให้ $ A = \ lbrace 1, 2, 6 \ rbrace $ และ $ B = \ lbrace 6, 12, 42 \ rbrace $ มีองค์ประกอบทั่วไป '6' ดังนั้นชุดเหล่านี้จึงเป็นชุดที่ทับซ้อนกัน

ชุดไม่ปะติดปะต่อ

ชุด A และ B สองชุดเรียกว่าชุดที่ไม่ปะติดปะต่อกันหากไม่มีองค์ประกอบที่เหมือนกันแม้แต่ชิ้นเดียว ดังนั้นชุดที่ไม่ปะติดปะต่อจึงมีคุณสมบัติดังต่อไปนี้ -

$ n (A \ cap B) = \ emptyset $
$ n (A \ cup B) = n (A) + n (B) $

Example - ให้ $ A = \ lbrace 1, 2, 6 \ rbrace $ และ $ B = \ lbrace 7, 9, 14 \ rbrace $ ไม่มีองค์ประกอบร่วมเพียงองค์ประกอบเดียวดังนั้นชุดเหล่านี้จึงเป็นเซตที่ทับซ้อนกัน

เวนน์ไดอะแกรม

แผนภาพเวนน์ประดิษฐ์ขึ้นในปี พ.ศ. 2423 โดยจอห์นเวนน์เป็นแผนภาพที่แสดงความสัมพันธ์เชิงตรรกะที่เป็นไปได้ทั้งหมดระหว่างชุดทางคณิตศาสตร์ที่แตกต่างกัน

Examples

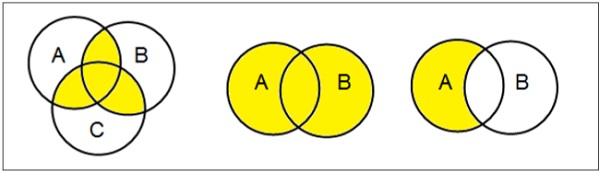
ตั้งค่าการทำงาน

การดำเนินการชุดประกอบด้วย Set Union, Set Intersection, Set Difference, Complement of Set และ Cartesian Product

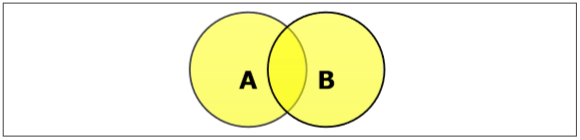
ตั้งสหภาพ

การรวมกันของชุด A และ B (แสดงโดย $ A \ cup B $) คือชุดขององค์ประกอบที่อยู่ใน A ใน B หรือทั้ง A และ B ดังนั้น $ A \ cup B = \ lbrace x \: | \: x \ ใน A \ OR \ x \ ใน B \ rbrace $.

Example- ถ้า $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ และ B = $ \ lbrace 13, 14, 15 \ rbrace $ แล้ว $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (องค์ประกอบร่วมเกิดขึ้นเพียงครั้งเดียว)

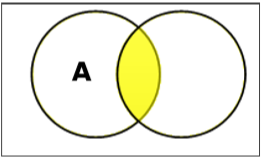
ตั้งค่าทางแยก

จุดตัดของชุด A และ B (แสดงโดย $ A \ cap B $) คือชุดขององค์ประกอบที่อยู่ในทั้ง A และ B ดังนั้น $ A \ cap B = \ lbrace x \: | \: x \ ใน A \ AND \ x \ ใน B \ rbrace $.

Example - ถ้า $ A = \ lbrace 11, 12, 13 \ rbrace $ และ $ B = \ lbrace 13, 14, 15 \ rbrace $ แล้ว $ A \ cap B = \ lbrace 13 \ rbrace $

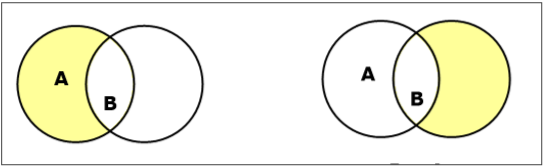
ตั้งค่าความแตกต่าง / ส่วนเสริมสัมพัทธ์

ความแตกต่างของเซต A และ B (แสดงโดย $ A - B $) คือชุดขององค์ประกอบที่อยู่ใน A เท่านั้น แต่ไม่ใช่ใน B ดังนั้น $ A - B = \ lbrace x \: | \: x \ ใน A \ AND \ x \ notin B \ rbrace $.

Example- ถ้า $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ และ $ B = \ lbrace 13, 14, 15 \ rbrace $ แล้ว $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ และ $ (B - A) = \ lbrace 14, 15 \ rbrace $ ที่นี่เราจะเห็น $ (A - B) \ ne (B - A) $

ส่วนเสริมของชุด

ส่วนประกอบของชุด A (แสดงโดย $ A '$) คือชุดขององค์ประกอบที่ไม่อยู่ในชุด A ดังนั้น $ A' = \ lbrace x | x \ notin A \ rbrace $.

โดยเฉพาะอย่างยิ่ง $ A '= (U - A) $ โดยที่ $ U $ เป็นชุดสากลที่มีวัตถุทั้งหมด

Example- ถ้า $ A = \ lbrace x \: | \: x \ \: {เป็นของ \: ถึง \: set \: of \: odd \: จำนวนเต็ม} \ rbrace $ แล้ว $ A '= \ lbrace y \: | \: y \ \: {does \: not \: belong \: to \: set \: of \: odd \: integers} \ rbrace $

ผลิตภัณฑ์คาร์ทีเซียน / ผลิตภัณฑ์ข้าม

ผลิตภัณฑ์คาร์ทีเซียนของ n จำนวนชุด $ A_1, A_2, \ dots A_n $ แสดงเป็น $ A_1 \ times A_2 \ dots \ times A_n $ สามารถกำหนดเป็นคู่คำสั่งที่เป็นไปได้ทั้งหมด $ (x_1, x_2, \ dots x_n) $ โดยที่ $ x_1 \ ใน A_1, x_2 \ ใน A_2, \ จุด x_n \ ใน A_n $

Example - ถ้าเราใช้สองชุด $ A = \ lbrace a, b \ rbrace $ และ $ B = \ lbrace 1, 2 \ rbrace $,

ผลคูณคาร์ทีเซียนของ A และ B เขียนเป็น - $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $

ผลคูณคาร์ทีเซียนของ B และ A เขียนเป็น - $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

ชุดไฟ

เซตกำลังของเซต S คือเซตของเซตย่อยทั้งหมดของ S รวมเซตว่าง คาร์ดินาลิตี้ของเซตกำลังของเซต S ของคาร์ดินาลิตี้ n คือ $ 2 ^ n $ ชุดไฟแสดงเป็น $ P (S) $

Example −

สำหรับชุด $ S = \ lbrace a, b, c, d \ rbrace $ ให้เราคำนวณชุดย่อย -

ชุดย่อยที่มีองค์ประกอบ 0 - $ \ lbrace \ emptyset \ rbrace $ (ชุดว่าง)
ชุดย่อยที่มี 1 องค์ประกอบ - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
ชุดย่อยที่มี 2 องค์ประกอบ - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
ชุดย่อยที่มี 3 องค์ประกอบ - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
ชุดย่อยที่มี 4 องค์ประกอบ - $ \ lbrace a, b, c, d \ rbrace $

ดังนั้น $ P (S) = $

$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 $

Note - ชุดไฟของชุดว่างก็เป็นชุดเปล่าเช่นกัน

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

การแบ่งส่วนของชุด

พาร์ติชันของชุดพูดSเป็นคอลเลกชันของnย่อยเคลื่อนพูด $ P_1, P_2, \ dots P_n $ ที่ตอบสนองความต่อไปนี้สามเงื่อนไข -

$ P_i $ ไม่มีชุดว่าง

$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
การรวมกันของส่วนย่อยต้องเท่ากับชุดเดิมทั้งหมด

$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
จุดตัดของชุดที่แตกต่างกันสองชุดว่างเปล่า

$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, สำหรับ \ a \ ne b \ ที่ไหน \ n \ ge a, \: b \ ge 0 \ rbrack $

Example

ให้ $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

การแบ่งพาร์ติชันที่เป็นไปได้อย่างหนึ่งคือ $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $

การแบ่งพาร์ติชันอื่นที่เป็นไปได้คือ $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $