การลดความซับซ้อนของฟังก์ชันบูลีน

การลดความซับซ้อนโดยใช้ฟังก์ชันพีชคณิต

ในวิธีนี้นิพจน์บูลีนหนึ่งนิพจน์จะถูกย่อให้เล็กลงเป็นนิพจน์ที่เท่ากันโดยใช้ข้อมูลประจำตัวบูลีน

ปัญหา 1

ลดนิพจน์บูลีนต่อไปนี้โดยใช้ข้อมูลประจำตัวบูลีน -

$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$

วิธีการแก้

ระบุ$ F (A, B, C) = A'B + BC '+ BC + AB'C' $

หรือ$ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$

[ตามกฎหมาย idempotent BC '= BC' + BC ']

หรือ$ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $

หรือ$ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $

[ตามกฎหมายการกระจาย]

หรือ$ F (A, B, C) = A'B + B.1 + C '(B + A) $

[(C '+ C) = 1 และกฎการดูดซึม (B + AB') = (B + A)]

หรือ$ F (A, B, C) = A'B + B + C '(B + A) $

[B.1 = B]

หรือ$ F (A, B, C) = B (A '+ 1) + C' (B + A) $

หรือ$ F (A, B, C) = B.1 + C '(B + A) $

[(A '+ 1) = 1]

หรือ$ F (A, B, C) = B + C '(B + A) $

[ณ B.1 = B]

หรือ$ F (A, B, C) = B + BC '+ AC' $

หรือ$ F (A, B, C) = B (1 + C ') + AC' $

หรือ$ F (A, B, C) = B.1 + AC '$

[เป็น (1 + C ') = 1]

หรือ$ F (A, B, C) = B + AC '$

[ณ B.1 = B]

ดังนั้น$ F (A, B, C) = B + AC '$ คือรูปแบบย่อขนาด

ปัญหา 2

ลดนิพจน์บูลีนต่อไปนี้โดยใช้ข้อมูลประจำตัวบูลีน -

$$ F (A, B, C) = (A + B) (A + C) $$

วิธีการแก้

ให้ $ F (A, B, C) = (A + B) (A + C) $

หรือ $ F (A, B, C) = AA + AC + BA + BC $ [การใช้กฎการกระจาย]

หรือ $ F (A, B, C) = A + AC + BA + BC $ [การบังคับใช้กฎหมาย Idempotent]

หรือ $ F (A, B, C) = A (1 + C) + BA + BC $ [การใช้กฎหมายการกระจาย]

หรือ $ F (A, B, C) = A + BA + BC $ [ใช้กฎหมายการครอบงำ]

หรือ $ F (A, B, C) = (A + 1) .A + BC $ [ใช้กฎหมายการกระจาย]

หรือ $ F (A, B, C) = 1.A + BC $ [ใช้กฎหมายการครอบงำ]

หรือ $ F (A, B, C) = A + BC $ [ใช้กฎหมายการครอบงำ]

ดังนั้น $ F (A, B, C) = A + BC $ คือรูปแบบย่อขนาด

แผนที่ Karnaugh

แผนที่คาร์นอห์ (K – map) ซึ่งนำเสนอโดยมอริซคาร์นอห์นในปี พ.ศ. 2496 เป็นการแสดงตารางความจริงแบบตารางซึ่งใช้เพื่อลดความซับซ้อนของนิพจน์พีชคณิตแบบบูลีน แผนที่ Karnaugh มีศูนย์และหนึ่งรายการในตำแหน่งที่ต่างกัน จัดให้มีการจัดกลุ่มนิพจน์บูลีนเข้าด้วยกันด้วยปัจจัยทั่วไปและกำจัดตัวแปรที่ไม่ต้องการออกจากนิพจน์ ในแผนที่ K การข้ามขอบเขตเซลล์ในแนวตั้งหรือแนวนอนเป็นการเปลี่ยนแปลงเพียงตัวแปรเดียวเสมอ

ตัวอย่าง 1

ตารางความจริงตามอำเภอใจอยู่ด้านล่าง -

ก	ข	การดำเนินการ B
0	0	ว
0	1	x
1	0	ย
1	1	z

ตอนนี้เราจะสร้าง k-map สำหรับตารางความจริงข้างต้น -

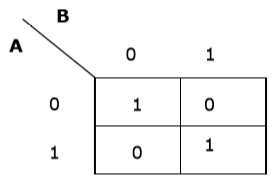
ตัวอย่าง 2

ตอนนี้เราจะสร้าง K-map สำหรับนิพจน์ - AB + A'B '

การทำให้ง่ายขึ้นโดยใช้ K-map

K-map ใช้กฎบางประการสำหรับการทำให้นิพจน์บูลีนง่ายขึ้นโดยการรวมเซลล์ที่อยู่ติดกันเข้าด้วยกันเป็นคำเดียว กฎอธิบายไว้ด้านล่าง -

Rule 1 - เซลล์ใด ๆ ที่มีศูนย์ไม่สามารถจัดกลุ่มได้

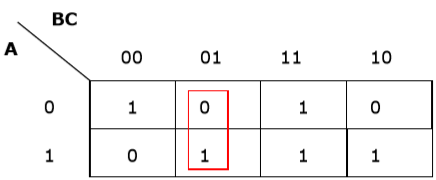
การจัดกลุ่มผิด

Rule 2 - กลุ่มต้องมี 2n เซลล์ (n เริ่มจาก 1)

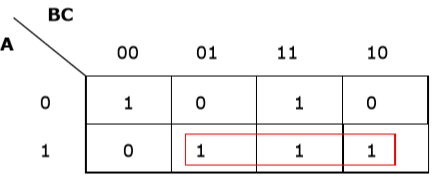
การจัดกลุ่มผิด

Rule 3 - การจัดกลุ่มต้องเป็นแนวนอนหรือแนวตั้ง แต่ต้องไม่เป็นแนวทแยง

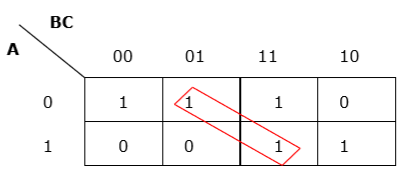
การจัดกลุ่มเส้นทแยงมุมไม่ถูกต้อง

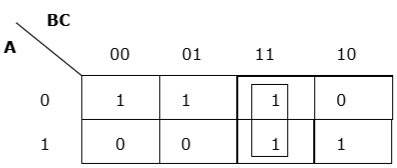
การจัดกลุ่มแนวตั้งที่เหมาะสม

การจัดกลุ่มแนวนอนที่เหมาะสม

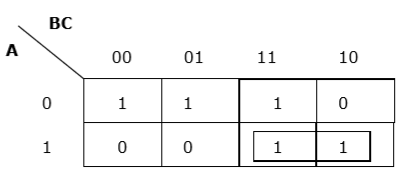
Rule 4 - กลุ่มต่างๆต้องได้รับการคุ้มครองให้มากที่สุด

การจัดกลุ่มไม่เพียงพอ

การจัดกลุ่มที่เหมาะสม

Rule 5 - ถ้า 1 ในเซลล์ใด ๆ ไม่สามารถจัดกลุ่มกับเซลล์อื่นได้เซลล์นั้นจะทำหน้าที่เป็นกลุ่มเอง

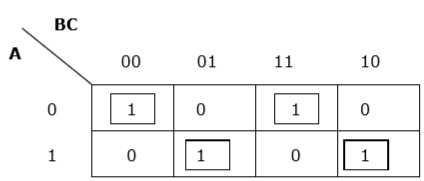
การจัดกลุ่มที่เหมาะสม

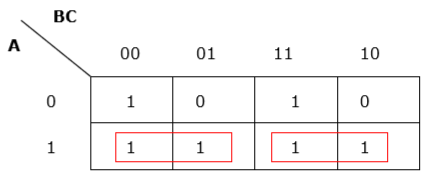
Rule 6 - กลุ่มอาจทับซ้อนกัน แต่ควรมีกลุ่มน้อยที่สุด

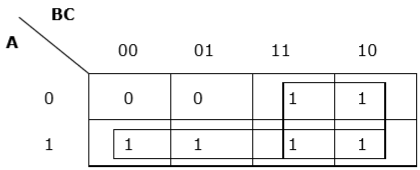
การจัดกลุ่มที่เหมาะสม

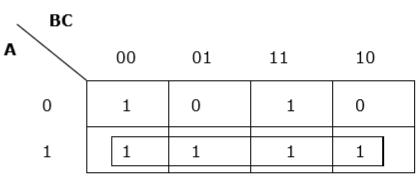
Rule 7 - เซลล์ / เซลล์ซ้ายสุดสามารถจัดกลุ่มด้วยเซลล์ / เซลล์ขวาสุดและเซลล์ / เซลล์บนสุดสามารถจัดกลุ่มด้วยเซลล์ / เซลล์ล่างสุด

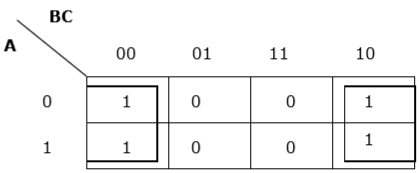
การจัดกลุ่มที่เหมาะสม

ปัญหา

ย่อนิพจน์บูลีนต่อไปนี้โดยใช้ K-map -

$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$

วิธีการแก้

แต่ละคำใส่ลงใน k-map และเราจะได้รับสิ่งต่อไปนี้ -

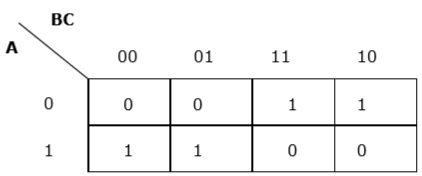
K-map สำหรับ F (A, B, C)

ตอนนี้เราจะจัดกลุ่มเซลล์ 1 ตามกฎที่ระบุไว้ข้างต้น -

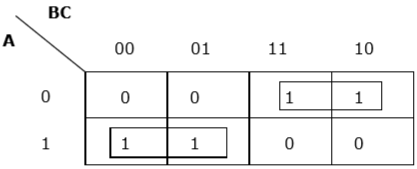
K-map สำหรับ F (A, B, C)

เรามีสองกลุ่มซึ่งเรียกว่า $ A'B $ และ $ AB '$ ดังนั้น $ F (A, B, C) = A'B + AB '= A \ oplus B $ เป็นรูปแบบย่อส่วน