คณิตศาสตร์ไม่ต่อเนื่อง - เพิ่มเติมเกี่ยวกับกราฟ

การระบายสีกราฟ

การระบายสีกราฟเป็นขั้นตอนของการกำหนดสีให้กับจุดยอดแต่ละจุดของกราฟ G เพื่อให้ไม่มีจุดยอดที่อยู่ติดกันได้สีเดียวกัน มีวัตถุประสงค์เพื่อลดจำนวนสีในขณะที่ระบายสีกราฟ จำนวนสีที่น้อยที่สุดที่ต้องใช้ในการระบายสีกราฟ G เรียกว่าจำนวนสีของกราฟนั้น ปัญหาการระบายสีกราฟเป็นปัญหา NP Complete

วิธีการระบายสีกราฟ

ขั้นตอนที่จำเป็นในการระบายสีกราฟ G ด้วยจำนวนจุดยอด n มีดังนี้ -

Step 1 - จัดเรียงจุดยอดของกราฟตามลำดับ

Step 2 - เลือกจุดยอดแรกและระบายสีด้วยสีแรก

Step 3- เลือกจุดยอดถัดไปและระบายสีด้วยสีที่มีตัวเลขต่ำสุดที่ไม่ได้ถูกระบายสีบนจุดยอดใด ๆ ที่อยู่ติดกับจุดยอดนั้น หากจุดยอดที่อยู่ติดกันทั้งหมดมีสีด้วยสีนี้ให้กำหนดสีใหม่ ทำซ้ำขั้นตอนนี้จนกว่าจุดยอดทั้งหมดจะเป็นสี

Example

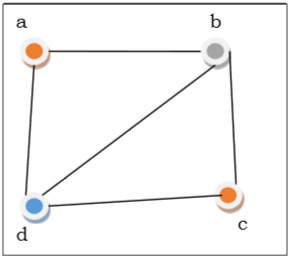
ในรูปด้านบนที่จุดยอดแรก $ a $ เป็นสีแดง เนื่องจากจุดยอดที่อยู่ติดกันของจุดยอด a อยู่ติดกันอีกครั้งจุดยอด $ b $ และจุดยอด $ d $ จึงมีสีต่างกันสีเขียวและสีน้ำเงินตามลำดับ จากนั้นจุดยอด $ c $ จะมีสีเป็นสีแดงเนื่องจากไม่มีจุดยอดที่อยู่ติดกันของ $ c $ เป็นสีแดง ดังนั้นเราสามารถระบายสีกราฟได้ 3 สี ดังนั้นจำนวนสีของกราฟคือ 3

การประยุกต์ใช้การระบายสีกราฟ

แอพพลิเคชั่นของการระบายสีกราฟ ได้แก่ -

• ลงทะเบียนการจัดสรร
• ระบายสีแผนที่
• การตรวจสอบกราฟ Bipartite
• การกำหนดความถี่วิทยุมือถือ
• ทำตารางเวลา ฯลฯ

กราฟ Traversal

การข้ามผ่านกราฟเป็นปัญหาในการเยี่ยมชมจุดยอดทั้งหมดของกราฟตามลำดับที่เป็นระบบ ส่วนใหญ่มีสองวิธีในการสำรวจกราฟ

• การค้นหาแรกกว้าง
• การค้นหาครั้งแรกเชิงลึก

การค้นหาแรกกว้าง

Breadth First Search (BFS) เริ่มต้นที่ระดับเริ่มต้น -0 จุดยอด $ X $ ของกราฟ $ G $ จากนั้นเราไปที่จุดยอดทั้งหมดที่เป็นเพื่อนบ้านของ $ X $ หลังจากเยี่ยมชมแล้วเราทำเครื่องหมายจุดยอดเป็น "เยี่ยมชม" และวางไว้ในระดับ -1 จากนั้นเราจะเริ่มจากจุดยอดระดับ 1 และใช้วิธีการเดียวกันกับทุกจุดยอดระดับ 1 และอื่น ๆ การข้ามผ่าน BFS จะสิ้นสุดเมื่อทุกจุดยอดของกราฟถูกเยี่ยมชม

BFS Algorithm

แนวคิดคือการเยี่ยมชมจุดยอดเพื่อนบ้านทั้งหมดก่อนที่จะเยี่ยมชมจุดยอดเพื่อนบ้านอื่น ๆ ของจุดยอดเพื่อนบ้าน

• เริ่มต้นสถานะของโหนดทั้งหมดเป็น“ พร้อม”

• ใส่จุดยอดต้นทางในคิวและเปลี่ยนสถานะเป็น "กำลังรอ"

• ทำซ้ำสองขั้นตอนต่อไปนี้จนกว่าคิวจะว่าง -

  • ลบจุดยอดแรกออกจากคิวและทำเครื่องหมายว่า "เยี่ยมแล้ว"

  • เพิ่มที่ด้านหลังของคิวเพื่อนบ้านทั้งหมดของจุดยอดที่ถูกลบซึ่งมีสถานะ "พร้อม" ทำเครื่องหมายสถานะเป็น "กำลังรอ"

Problem

ให้เราใช้กราฟ (จุดยอดต้นทางคือ 'a') และใช้อัลกอริทึม BFS เพื่อค้นหาลำดับการข้ามผ่าน

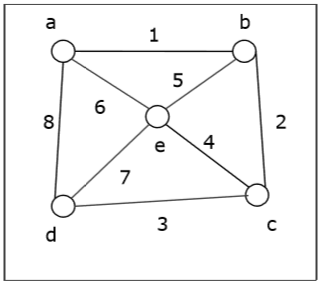
Solution -

• เริ่มต้นสถานะของจุดยอดทั้งหมดเป็น“ พร้อม”

• ใส่ในคิวและเปลี่ยนสถานะเป็น“รอ”

• นำจากคิวทำเครื่องหมายว่าเป็น“ผู้เข้าชม”

• เพิ่มเพื่อนบ้านใน ‘พร้อม’ รัฐB, DและEที่ส่วนท้ายของคิวและทำเครื่องหมายว่า ‘รอ’

• ลบbออกจากคิวทำเครื่องหมายว่า "เยี่ยมแล้ว" ใส่เพื่อนบ้าน "พร้อม" cที่ท้ายคิวและทำเครื่องหมายcเป็น "กำลังรอ"

• ลบdออกจากคิวและทำเครื่องหมายว่า "เยี่ยมแล้ว" ไม่มีเพื่อนบ้านอยู่ในสถานะ“ พร้อม”

• ลบeออกจากคิวและทำเครื่องหมายว่า "เยี่ยมแล้ว" ไม่มีเพื่อนบ้านอยู่ในสถานะ“ พร้อม”

• ลบcออกจากคิวและทำเครื่องหมายว่า "เยี่ยมแล้ว" ไม่มีเพื่อนบ้านอยู่ในสถานะ“ พร้อม”

• คิวว่างจึงหยุด

ดังนั้นลำดับการส่งผ่านคือ -

$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $

คำสั่งอื่นของการส่งผ่านคือ -

$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

หรือ$ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $

หรือ$ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $

หรือ$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

หรือ$ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Application of BFS

• ค้นหาเส้นทางที่สั้นที่สุด
• ต้นไม้ที่ครอบคลุมขั้นต่ำสำหรับกราฟที่ไม่มีการถ่วงน้ำหนัก
• ระบบนำทาง GPS
• การตรวจจับรอบในกราฟที่ไม่มีทิศทาง
• ค้นหาโหนดทั้งหมดภายในส่วนประกอบที่เชื่อมต่อกัน

Complexity Analysis

ให้ $ G (V, E) $ เป็นกราฟที่มี $ | V | $ จำนวนจุดยอดและ $ | E | $ จำนวนขอบ หากอัลกอริทึมการค้นหาแรกกว้างเข้าชมทุกจุดยอดในกราฟและตรวจสอบทุกขอบความซับซ้อนของเวลาจะเป็น -

$$ O (| V | + | E |). O (| E |) $$

อาจแตกต่างกันระหว่าง $ O (1) $ และ $ O (| V2 |) $

การค้นหาครั้งแรกเชิงลึก

อัลกอริธึม Depth First Search (DFS) เริ่มต้นจากจุดยอด $ v $ จากนั้นจะข้ามไปยังจุดยอดที่อยู่ติดกัน (พูด x) ที่ไม่เคยเยี่ยมชมมาก่อนและทำเครื่องหมายเป็น "เยี่ยมชม" และไปต่อด้วยจุดยอดที่อยู่ติดกันที่ $ x $ และ เป็นต้น.

หากอยู่ที่จุดยอดใดจุดยอดหนึ่งพบว่ามีการเยี่ยมชมจุดยอดที่อยู่ติดกันทั้งหมดจากนั้นจะย้อนกลับไปจนกว่าจะพบจุดยอดแรกที่มีจุดยอดที่อยู่ติดกันซึ่งยังไม่เคยข้ามผ่านมาก่อน จากนั้นมันจะเคลื่อนผ่านจุดยอดนั้นไปเรื่อย ๆ โดยมีจุดยอดที่อยู่ติดกันจนกว่ามันจะข้ามผ่านจุดยอดเยี่ยมทั้งหมดและต้องย้อนรอยอีกครั้ง ด้วยวิธีนี้มันจะข้ามจุดยอดทั้งหมดที่เข้าถึงได้จากจุดยอดเริ่มต้น $ v $

DFS Algorithm

แนวคิดคือการเยี่ยมชมจุดยอดเพื่อนบ้านทั้งหมดของจุดยอดเพื่อนบ้านก่อนที่จะไปเยี่ยมชมจุดยอดเพื่อนบ้านอื่น ๆ

• เริ่มต้นสถานะของโหนดทั้งหมดเป็น“ พร้อม”

• ใส่จุดยอดต้นทางในสแต็กและเปลี่ยนสถานะเป็น "กำลังรอ"

• ทำซ้ำสองขั้นตอนต่อไปนี้จนกว่าสแต็กจะว่างเปล่า -

  • นำจุดยอดบนสุดออกจากสแต็กและทำเครื่องหมายเป็น "เยี่ยมชม"

  • ดันไปที่ด้านบนสุดของสแต็กเพื่อนบ้านทั้งหมดของจุดยอดที่ถูกลบซึ่งมีสถานะ "พร้อม" ทำเครื่องหมายสถานะเป็น "กำลังรอ"

Problem

ให้เราใช้กราฟ (จุดยอดที่มาคือ 'a') และใช้อัลกอริทึม DFS เพื่อค้นหาลำดับการข้ามผ่าน

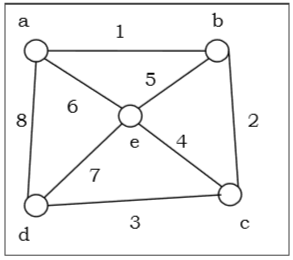
Solution

• เริ่มต้นสถานะของจุดยอดทั้งหมดเป็น“ พร้อม”

• ผลักดันในกองและเปลี่ยนสถานะเป็น“รอ”

• Pop และทำเครื่องหมายเป็น“ผู้เข้าชม”

• ผลักดันเพื่อนบ้าน ‘ใน‘พร้อม’รัฐE, DและBไปด้านบนของสแต็คและทำเครื่องหมายว่า‘รอ’

• ป๊อปbจากสแต็กทำเครื่องหมายเป็น "เยี่ยมแล้ว" ดันเพื่อนบ้าน "พร้อม" cลงบนสแต็ก

• ป๊อปcจากสแต็กและทำเครื่องหมายเป็น "เยี่ยมชม" ไม่มีเพื่อนบ้านที่“ พร้อม”

• ป๊อปdจากสแต็กและทำเครื่องหมายเป็น "เยี่ยมชม" ไม่มีเพื่อนบ้านที่“ พร้อม”

• ป๊อปeจากสแต็กและทำเครื่องหมายเป็น "เยี่ยมชม" ไม่มีเพื่อนบ้านที่“ พร้อม”

• สแต็คว่างเปล่า ดังนั้นหยุดเถอะ

ดังนั้นลำดับการส่งผ่านคือ -

$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $

คำสั่งอื่นของการส่งผ่านคือ -

$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $

หรือ$ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $

หรือ$ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

หรือ$ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $

หรือ$ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $

Complexity Analysis

ให้ $ G (V, E) $ เป็นกราฟที่มี $ | V | $ จำนวนจุดยอดและ $ | E | $ จำนวนขอบ หากอัลกอริทึม DFS เข้าชมทุกจุดยอดในกราฟและตรวจสอบทุกขอบความซับซ้อนของเวลาคือ -

$$ \ circleddash (| V | + | E |) $$

Applications

• การตรวจจับวงจรในกราฟ
• เพื่อค้นหาการเรียงลำดับโทโพโลยี
• เพื่อทดสอบว่ากราฟเป็นสองฝ่ายหรือไม่
• ค้นหาส่วนประกอบที่เชื่อมต่อ
• การหาสะพานของกราฟ
• ค้นหา bi-connectivity ในกราฟ
• การแก้ปัญหาทัวร์อัศวิน
• การแก้ปริศนาด้วยวิธีแก้ปัญหาเดียว