คณิตศาสตร์ไม่ต่อเนื่อง - ต้นไม้ที่ทอดยาว
ต้นไม้ที่ทอดของกราฟที่ไม่มีทิศทางที่เชื่อมต่อ $ G $ คือต้นไม้ที่รวมจุดยอดทั้งหมดของ $ G $ ไว้น้อยที่สุด กราฟอาจมีต้นไม้ที่ทอดยาวมากมาย
ตัวอย่าง
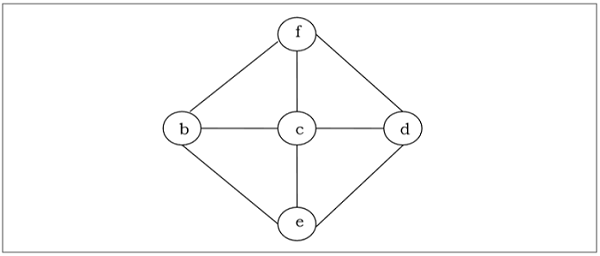
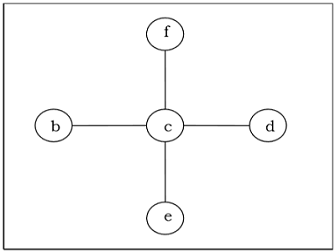
ต้นไม้ระยะขั้นต่ำ
ต้นไม้ทอดที่มีน้ำหนักที่กำหนดน้อยกว่าหรือเท่ากับน้ำหนักของกราฟที่มีน้ำหนักเชื่อมต่อและไม่ได้กำหนดทิศทาง $ G $ เรียกว่าต้นไม้ระยะต่ำสุด (MST) น้ำหนักของต้นไม้ทอดคือผลรวมของน้ำหนักทั้งหมดที่กำหนดให้กับขอบแต่ละด้านของต้นไม้ที่ทอด
ตัวอย่าง
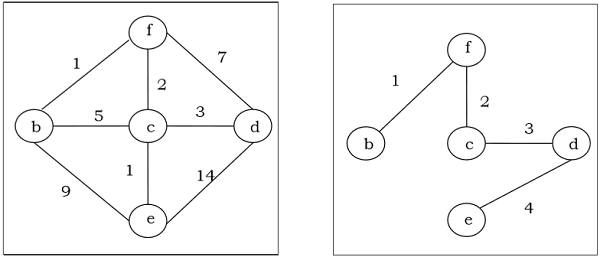
อัลกอริทึมของ Kruskal
อัลกอริทึมของ Kruskal เป็นอัลกอริธึมแบบละโมบที่ค้นหาต้นไม้ที่มีระยะเวลาขั้นต่ำสำหรับกราฟถ่วงน้ำหนักที่เชื่อมต่อ พบต้นไม้ของกราฟนั้นซึ่งรวมทุกจุดยอดและน้ำหนักรวมของขอบทั้งหมดในต้นไม้นั้นน้อยกว่าหรือเท่ากับต้นไม้ที่ทอดเป็นไปได้ทั้งหมด
อัลกอริทึม
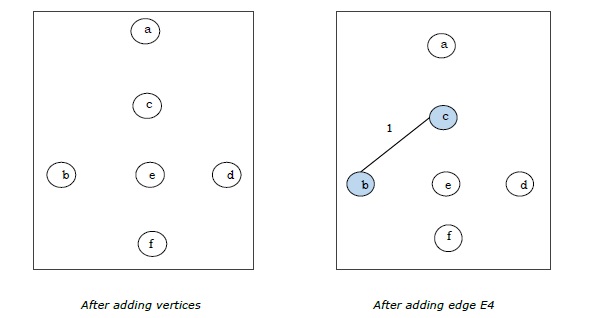
Step 1 - จัดเรียงขอบทั้งหมดของกราฟที่กำหนด $ G (V, E) $ จากน้อยไปมากตามน้ำหนักขอบ
Step 2 - เลือกขอบถ่วงน้ำหนักที่เล็กที่สุดจากกราฟและตรวจสอบว่ามันก่อตัวเป็นวัฏจักรโดยมีต้นไม้ทอดที่ก่อตัวขึ้นจนถึงตอนนี้หรือไม่
Step 3 - หากไม่มีรอบให้รวมขอบนี้เข้ากับต้นไม้ที่ทอดแล้วทิ้ง
Step 4 - ทำซ้ำขั้นตอนที่ 2 และขั้นตอนที่ 3 จนกว่า $ (V-1) $ จำนวนขอบจะเหลืออยู่ในต้นไม้ที่ทอด
Problem
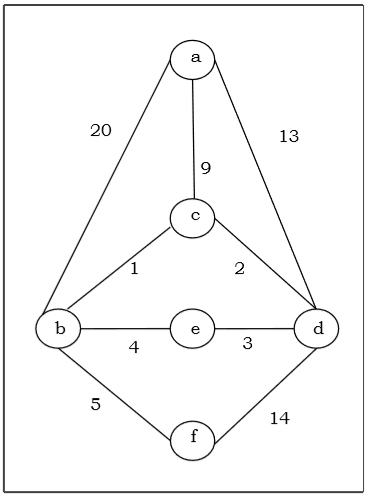
สมมติว่าเราต้องการหาโครงสร้างสแปนนิงขั้นต่ำสำหรับกราฟ G ต่อไปนี้โดยใช้อัลกอริทึมของ Kruskal
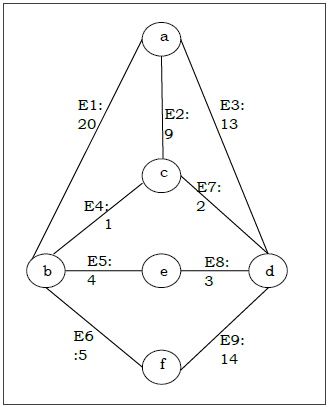
Solution
จากกราฟด้านบนเราสร้างตารางต่อไปนี้ -
| ขอบเลขที่ | คู่เวอร์เท็กซ์ | น้ำหนักขอบ |
|---|---|---|
| E1 | (ก, ข) | 20 |
| E2 | (ก, ค) | 9 |
| E3 | (ก, ง) | 13 |
| E4 | (ข, ค) | 1 |
| E5 | (ข, จ) | 4 |
| E6 | (ข, ฉ) | 5 |
| E7 | (ค, ง) | 2 |
| E8 | (ง, จ) | 3 |
| E9 | (ง, ฉ) | 14 |
ตอนนี้เราจะจัดเรียงตารางใหม่ตามลำดับจากน้อยไปหามากตามน้ำหนักขอบ -
| ขอบเลขที่ | คู่เวอร์เท็กซ์ | น้ำหนักขอบ |
|---|---|---|
| E4 | (ข, ค) | 1 |
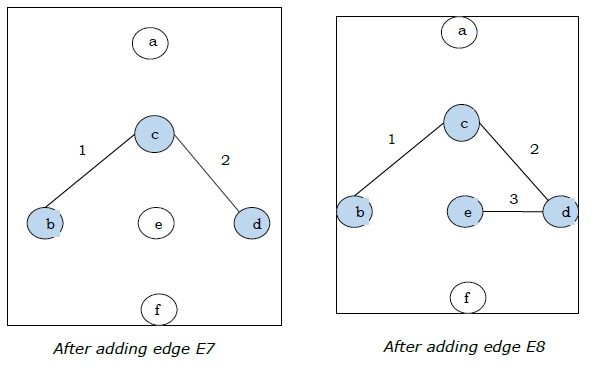
| E7 | (ค, ง) | 2 |
| E8 | (ง, จ) | 3 |
| E5 | (ข, จ) | 4 |
| E6 | (ข, ฉ) | 5 |
| E2 | (ก, ค) | 9 |
| E3 | (ก, ง) | 13 |
| E9 | (ง, ฉ) | 14 |
| E1 | (ก, ข) | 20 |
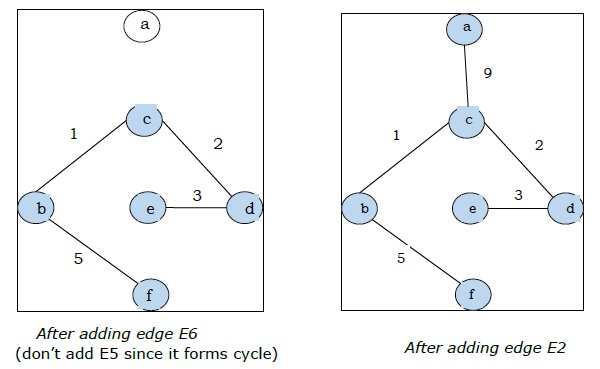
เนื่องจากเราได้ขอบทั้ง 5 ด้านในรูปสุดท้ายเราจึงหยุดอัลกอริทึมและนี่คือต้นไม้ที่มีการขยายน้อยที่สุดและน้ำหนักรวมคือ $ (1 + 2 + 3 + 5 + 9) = 20 $
อัลกอริทึมของ Prim
อัลกอริทึมของ Prim ค้นพบในปี 1930 โดยนักคณิตศาสตร์ Vojtech Jarnik และ Robert C. พบต้นไม้ของกราฟนั้นซึ่งรวมทุกจุดยอดและน้ำหนักรวมของขอบทั้งหมดในต้นไม้นั้นน้อยกว่าหรือเท่ากับต้นไม้ที่ทอดเป็นไปได้ทั้งหมด อัลกอริทึมของ Prim เร็วกว่าบนกราฟที่หนาแน่น
อัลกอริทึม
เริ่มต้นต้นไม้ที่ทอดน้อยที่สุดด้วยจุดยอดเดียวโดยสุ่มเลือกจากกราฟ
ทำซ้ำขั้นตอนที่ 3 และ 4 จนกว่าจุดยอดทั้งหมดจะรวมอยู่ในแผนภูมิ
เลือกขอบที่เชื่อมต่อต้นไม้กับจุดยอดที่ยังไม่ได้อยู่ในต้นไม้เพื่อให้น้ำหนักของขอบน้อยที่สุดและการรวมขอบจะไม่ก่อให้เกิดวัฏจักร
เพิ่มขอบที่เลือกและจุดยอดที่เชื่อมต่อกับต้นไม้
Problem
สมมติว่าเราต้องการหาโครงสร้างสแปนนิงขั้นต่ำสำหรับกราฟ G ต่อไปนี้โดยใช้อัลกอริทึมของ Prim
Solution
ที่นี่เราเริ่มต้นด้วยจุดยอด 'a' และดำเนินการต่อ
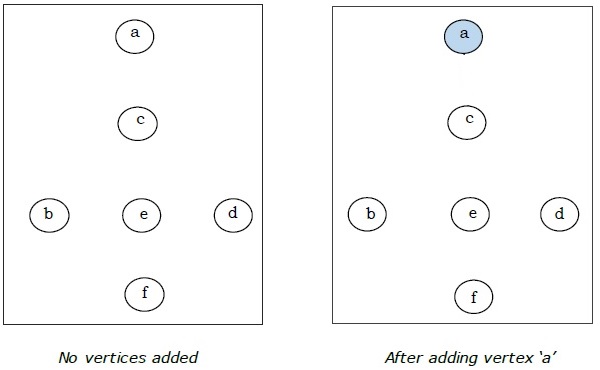
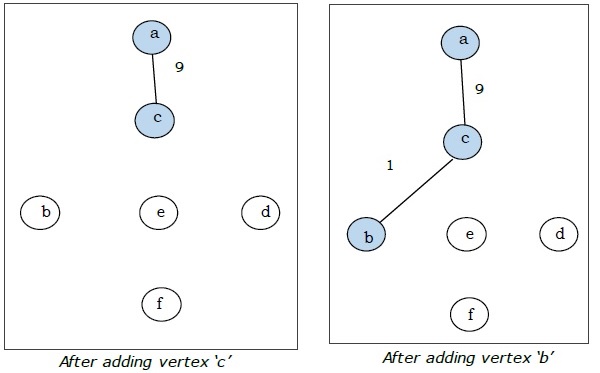
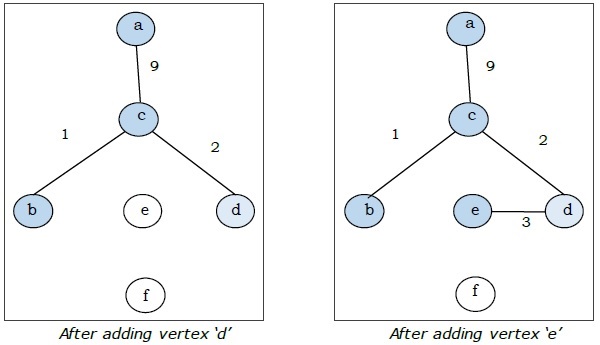
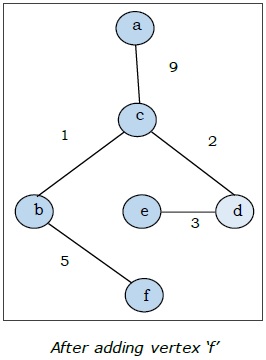
นี่คือต้นไม้ที่ทอดน้อยที่สุดและน้ำหนักรวมคือ $ (1 + 2 + 3 + 5 + 9) = 20 $