Digitale Schaltungen - Schwellenwertlogik
In den vorherigen Kapiteln haben wir verschiedene kombinatorische Schaltungen unter Verwendung von Logikgattern implementiert. Mit Ausnahme des NICHT-Gatters haben die verbleibenden alle Logikgatter mindestens zwei Eingänge und einen einzelnen Ausgang. Ebenso diethreshold gate enthält auch mindestens einen Eingang und nur einen Ausgang.
Zusätzlich enthält es die jeweiligen Gewichte für jeden Eingang und einen Schwellenwert. Die Werte dieser Gewichte und Schwellenwerte können eine beliebige endliche reelle Zahl sein.
Grundlagen des Schwellentors
Die Eingänge des Schwellenwertgatters seien X 1 , X 2 , X 3 ,…, X n . Die entsprechenden Gewichte dieser Eingänge sind W 1 , W 2 , W 3 ,…, W n . Dassymbol of Threshold Gate ist in der folgenden Abbildung dargestellt.
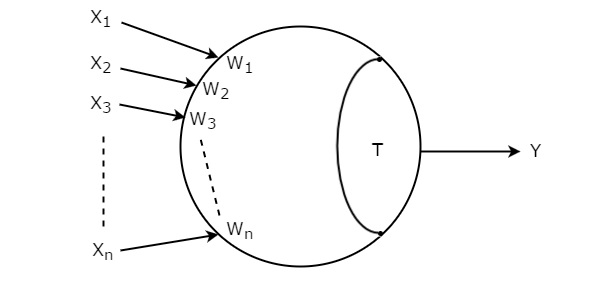
Threshold gatewird mit einem Kreis dargestellt und hat 'n' Eingänge, X 1 bis X n und einen einzelnen Ausgang, Y. Dieser Kreis besteht aus zwei Teilen. Ein Teil repräsentiert die den Eingaben entsprechenden Gewichte und der andere Teil repräsentiert den Schwellenwert T.
Die Summe der Produkte von Inputs mit entsprechenden Gewichten ist bekannt als weighted sum. Wenn diese gewichtete Summe größer oder gleich dem Schwellenwert T ist, ist nur die Ausgabe Y gleich eins. Andernfalls ist der Ausgang Y gleich Null.
Mathematicallykönnen wir diese Beziehung zwischen den Eingängen und dem Ausgang des Schwellenwertgatters wie folgt schreiben.
$$ Y = 1, wenn \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
Sonst = 0.
Daher können wir verschiedene Logikgatter und Boolesche Funktionen implementieren, indem wir einfach die Werte der Gewichte und / oder des Schwellenwerts T ändern.
Beispiel
Lassen Sie uns die finden simplified Boolean function für das folgende Schwellentor.

Dieses Schwellenwertgatter hat drei Eingänge X 1 , X 2 , X 3 und einen Ausgang Y.
Die den Eingaben X 1 , X 2 und X 3 entsprechenden Gewichte sind W 1 = 2, W 2 = 1 und W 3 = -4.
Der Wert des Schwellenwertgatters ist T = -1.
Das weighted sum des Schwellentors ist
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Ersetzen Sie die angegebenen Gewichte durch die obige Gleichung.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
Die Ausgabe des Schwellenwertgatters Y ist '1', wenn W ≥ –1 ist, andernfalls ist es '0'.
Folgende table zeigt die Beziehung zwischen Eingabe und Ausgabe für alle möglichen Kombinationen von Eingaben.
| Eingänge | Gewichtete Summe | Ausgabe | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Aus der obigen Tabelle können wir die schreiben Boolean function für die Ausgabe Y als
$$ Y = \ sum m \ left (0,2,4,6,7 \ right) $$
Die Vereinfachung dieser Booleschen Funktion mit 3 variable K-Map ist in der folgenden Abbildung dargestellt.

deshalb, die simplified Boolean function für ein gegebenes Schwellenwert-Gate ist $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Synthese von Schwellenfunktionen
Das Schwellentor wird auch als bezeichnet universal gateweil wir jede Boolesche Funktion mit Threshold Gate (s) implementieren können. Manchmal ist es möglicherweise nicht möglich, wenige Logikgatter und Boolesche Funktionen mithilfe eines einzelnen Schwellenwertgatters zu implementieren. In diesem Fall benötigen wir möglicherweise mehrere Threshold-Gates.
Folge diesen steps zum Implementieren einer Booleschen Funktion unter Verwendung eines einzelnen Schwellenwertgatters.
Step 1 - Formulieren Sie a Truth table für gegebene Boolesche Funktion.
Step 2 - Fügen Sie in der obigen Wahrheitstabelle eine weitere Spalte hinzu (schließen Sie sie ein), die die Beziehung zwischen angibt weighted sums und Threshold value.
Step 3 - Schreiben Sie die Beziehung zwischen gewichteten Summen und Schwellenwert für jede Kombination von Eingaben wie unten erwähnt.
Wenn die Ausgabe der Booleschen Funktion 1 ist, ist die gewichtete Summe größer oder gleich dem Schwellenwert für diese Kombination von Eingaben.
Wenn die Ausgabe der Booleschen Funktion 0 ist, ist die gewichtete Summe kleiner als der Schwellenwert für diese Kombination von Eingaben.
Step 4 - Wählen Sie die Werte für Gewicht und Schwellenwert so aus, dass sie alle in der letzten Spalte der obigen Tabelle vorhandenen Beziehungen erfüllen.
step 5 - Zeichne die symbol des Schwellenwerttors mit diesen Gewichten und dem Schwellenwert.
Beispiel
Lassen Sie uns Folgendes implementieren Boolean function mit Single Threshold Gate.
$$ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $$
Die angegebene Boolesche Funktion ist eine Funktion mit drei Variablen, die in Form von Min-Termen dargestellt wird. DasTruth table dieser Funktion ist unten gezeigt.
| Eingänge | Ausgabe | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Fügen wir nun eine weitere Spalte zur obigen Wahrheitstabelle hinzu (schließen Sie sie ein). Diese letzte Spalte enthält die Beziehungen zwischenweighted sums (W) and Threshold Wert (T) für jede Kombination von Eingängen.
| Eingänge | Ausgabe | Beziehungen zwischen W & T. | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T. |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T. |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T. |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T. |
Es folgen die Schlussfolgerungen aus der obigen Tabelle.
Der Wert von Threshold sollte basierend auf der ersten Beziehung entweder Null oder negativ sein.
Der Wert von W 3 sollte basierend auf der ersten und zweiten Beziehung negativ sein.
Die Werte von W 1 und W 2 sollten basierend auf der fünften und dritten Beziehung größer oder gleich dem Schwellenwert sein.
W 2 sollte basierend auf der vierten Beziehung größer als W 3 sein .
Basierend auf den obigen Schlussfolgerungen können wir die folgenden Werte für Gewichte und Schwellenwerte auswählen.
W 1 = 2, W 2 = 1, W 3 = -4 & T = -1
Das symbol des Schwellenwertgatters mit den obigen Werten ist unten gezeigt.

Daher implementiert dieses Schwellenwerttor das Gegebene Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $.