नेटवर्क सिद्धांत - डेल्टा से स्टार रूपांतरण
पिछले अध्याय में, हमने एक उदाहरण समस्या संबंधित समकक्ष प्रतिरोध पर चर्चा की। वहां, हमने गणना कीequivalent resistanceदिए गए विद्युत नेटवर्क के टर्मिनलों ए और बी के बीच आसानी से। क्योंकि, प्रत्येक चरण में, हमें प्रतिरोधों का संयोजन मिला है जो या तो श्रृंखला रूप या समानांतर रूप से जुड़े हुए हैं।
हालांकि, कुछ स्थितियों में, पिछले दृष्टिकोण का पालन करके नेटवर्क को सरल बनाना मुश्किल है। उदाहरण के लिए, डेल्टा (form) फॉर्म या स्टार फॉर्म में जुड़े प्रतिरोधक। ऐसी स्थितियों में, हमें करना होगाconvertश्रृंखला संयोजन या समानांतर संयोजन का उपयोग करके इसे और सरल बनाने के लिए एक रूप से दूसरे तक का नेटवर्क। इस अध्याय में, हम के बारे में चर्चा करते हैंDelta to Star Conversion।
डेल्टा नेटवर्क
निम्नलिखित को धयान मे रखते हुए delta network जैसा कि निम्नलिखित आकृति में दिखाया गया है।
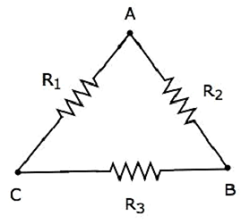
निम्नलिखित समीकरणों का प्रतिनिधित्व करते हैं equivalent resistance डेल्टा नेटवर्क के दो टर्मिनलों के बीच, जब तीसरा टर्मिनल खुला रखा जाता है।
$ $ R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $$
$ $ R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $$
$ $ R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $$
स्टार नेटवर्क
निम्नलिखित आंकड़ा दिखाता है equivalent star network उपरोक्त डेल्टा नेटवर्क के अनुरूप।
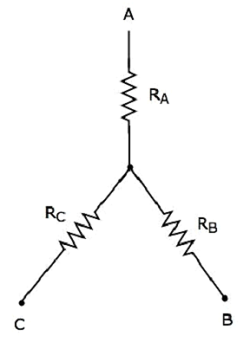
निम्नलिखित समीकरणों का प्रतिनिधित्व करते हैं equivalent resistance स्टार टर्मिनल के दो टर्मिनलों के बीच, जब तीसरा टर्मिनल खुला रखा जाता है।
$ $ R_ {AB} = R_A + R_B $ $
$$ R_ {BC} = R_B + R_C $$
$ $ R_ {CA} = R_C + R_A $$
डेल्टा नेटवर्क प्रतिरोधों के संदर्भ में स्टार नेटवर्क प्रतिरोध
हम उपरोक्त समीकरणों के दाएं हाथ की ओर के शब्दों को समान करते हुए निम्नलिखित समीकरण प्राप्त करेंगे, जिसके लिए बाएं हाथ की ओर की शर्तें समान हैं।
$ R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $ Equation 3
उपरोक्त तीन समीकरणों को जोड़कर हम प्राप्त करेंगे
$ $ 2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $ $
$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Equation 4
समीकरण 4 से समीकरण 2 को घटाएं।
$ R_A + R_B + R_C - (R_B + R_C) = \ frac {R_1 R_2 + R_2 + R_3 + R_3 R_1} {R_1 + R_2 + R_3} - \ f_1 {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $
$ $ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ $
समीकरण 4 से समीकरण 3 को घटाकर, हम प्राप्त करेंगे
$ $ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ $
समीकरण 4 से समीकरण 1 को घटाकर, हम प्राप्त करेंगे
$ $ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ $
उपरोक्त संबंधों का उपयोग करके, हम स्टार नेटवर्क के प्रतिरोध को डेल्टा नेटवर्क के प्रतिरोधों से पा सकते हैं। इस तरह, हम एक कन्वर्ट कर सकते हैंdelta network में star network।
उदाहरण
हमें गणना करते हैं resistances of star network, जो डेल्टा नेटवर्क के समतुल्य हैं जैसा कि निम्न आकृति में दिखाया गया है।
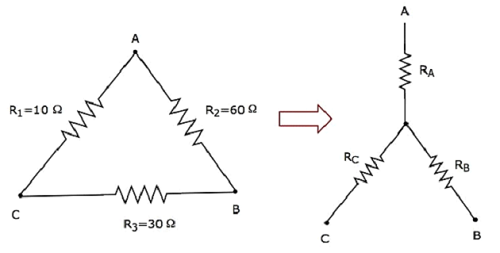
देखते हुए resistances of delta networkजैसा कि आर 1 = 10 Ω, आर 2 = 60 3 और आर 3 = 30 Ω।
हम डेल्टा नेटवर्क के प्रतिरोधों के संदर्भ में स्टार नेटवर्क के प्रतिरोधों के निम्नलिखित संबंधों को जानते हैं।
$ $ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ $
$ $ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ $
$ $ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ $
उपरोक्त समीकरणों में R 1 , R 2 और R 3 के मानों को बदलें।
$ $ R_A = \ frac {10 \ 60 बार} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$
$$ R_B = \ frac {60 \ गुना 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$
$ $ R_C = \ frac {30 \ गुना 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$
इसलिए, हमें स्टार नेटवर्क का प्रतिरोध मिला RA = 6 Ω, RB = 18 Ω तथा RC = 3 Ω, जो दिए गए डेल्टा नेटवर्क के प्रतिरोधों के बराबर हैं।