नेटवर्क टोपोलॉजी मैट्रिसेस
पिछले अध्याय में, हमने चर्चा की कि इलेक्ट्रिक सर्किट को समतुल्य ग्राफ में कैसे परिवर्तित किया जाए। अब, नेटवर्क टोपोलॉजी मेट्रिसेस पर चर्चा करते हैं जो किसी भी बिजली के सर्किट या नेटवर्क समस्या को उनके समतुल्य रेखांकन का उपयोग करके हल करने के लिए उपयोगी हैं।
नेटवर्क ग्राफ़ के साथ संबद्ध मैट्रिसेस
निम्नलिखित तीन मैट्रिक्स हैं जिनका उपयोग ग्राफ सिद्धांत में किया जाता है।
- घटना मैट्रिक्स
- मौलिक लूप मैट्रिक्स
- मौलिक कट सेट मैट्रिक्स
घटना मैट्रिक्स
एक घटना मैट्रिक्स किसी दिए गए विद्युत सर्किट या नेटवर्क के ग्राफ का प्रतिनिधित्व करता है। इसलिए, उसी इलेक्ट्रिक सर्किट या नेटवर्क के ग्राफ को खींचना संभव हैincidence matrix।
हम जानते हैं कि ग्राफ़ में नोड्स का एक सेट होता है और वे कुछ शाखाओं द्वारा जुड़े होते हैं। तो, शाखाओं को एक नोड से जोड़ने को घटना कहा जाता है। घटना मैट्रिक्स को अक्षर ए के साथ दर्शाया जाता है। इसे नोड से शाखा घटना मैट्रिक्स के रूप में भी कहा जाता हैnode incidence matrix।
यदि 'एन' नोड्स हैं और 'बी' शाखाएं मौजूद हैं directed graph, फिर घटना मैट्रिक्स में 'एन' पंक्तियां और 'बी' कॉलम होंगे। यहां, पंक्तियां और स्तंभ एक निर्देशित ग्राफ के नोड्स और शाखाओं के अनुरूप हैं। इसलिएorder घटना मैट्रिक्स की होगी n × b।
elements of incidence matrix इन तीन मूल्यों में से एक होगा, +1, -1 और 0।
यदि शाखा प्रवाह चयनित नोड से निकल रहा है, तो तत्व का मान +1 होगा।
यदि शाखा प्रवाह चयनित नोड की ओर प्रवेश कर रहा है, तो तत्व का मान -1 होगा।
यदि शाखा चालू न तो चयनित नोड में प्रवेश करती है और न ही चयनित नोड से निकलती है, तो तत्व का मान 0 होगा।
घटना मैट्रिक्स खोजने की प्रक्रिया
निर्देशित ग्राफ की घटना मैट्रिक्स को खोजने के लिए इन चरणों का पालन करें।
दिए गए निर्देशित ग्राफ़ के समय एक नोड का चयन करें और एक पंक्ति में उस नोड के अनुरूप घटना मैट्रिक्स के तत्वों के मूल्यों को भरें।
दिए गए निर्देशित ग्राफ के सभी नोड्स के लिए उपरोक्त चरण को दोहराएं।
उदाहरण
निम्नलिखित को धयान मे रखते हुए directed graph।

incidence matrix उपरोक्त निर्देशित ग्राफ के अनुसार होगा
$$ A = \ _ {bmatrix} -1 और 1 & 0 & -1 & 0 & 0 \\ 0 & -1 और 1 & 1 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & -1 और -1 एंड एंड {bmatrix} $$
उपरोक्त मैट्रिक्स की पंक्तियाँ और स्तंभ दिए गए निर्देशित ग्राफ के नोड्स और शाखाओं का प्रतिनिधित्व करते हैं। इस घटना मैट्रिक्स का क्रम 4 × 6 है।
उपरोक्त घटना मैट्रिक्स को देखकर, हम यह निष्कर्ष निकाल सकते हैं कि summationघटना मैट्रिक्स के स्तंभ तत्वों शून्य के बराबर है। इसका मतलब है, एक शाखा एक नोड से एक करंट छोड़ती है और केवल दूसरे एकल नोड में प्रवेश करती है।
Note- यदि दिया गया ग्राफ एक गैर-निर्देशित प्रकार है, तो इसे प्रत्येक शाखा पर तीर का प्रतिनिधित्व करके एक निर्देशित ग्राफ में परिवर्तित करें। हम प्रत्येक शाखा में वर्तमान प्रवाह की मनमानी दिशा पर विचार कर सकते हैं।
मौलिक लूप मैट्रिक्स
मौलिक पाश या f-loopएक लूप है, जिसमें केवल एक लिंक और एक या अधिक टहनियाँ होती हैं। तो, एफ-लूप की संख्या लिंक की संख्या के बराबर होगी। मौलिक लूप मैट्रिक्स को बी अक्षर से दर्शाया जाता हैfundamental circuit matrixऔर टाई-सेट मैट्रिक्स। यह मैट्रिक्स शाखा धाराओं और लिंक धाराओं के बीच संबंध देता है।
यदि 'एन' नोड्स हैं और 'बी' शाखाएं मौजूद हैं directed graph, फिर सह-वृक्ष में मौजूद लिंक की संख्या, जो दिए गए ग्राफ के चयनित पेड़ के अनुरूप है, b-n + 1 होगा।
तो, मौलिक लूप मैट्रिक्स में 'बी-एन + 1' पंक्तियां और 'बी' कॉलम होंगे। यहाँ, पंक्तियाँ और स्तंभ सह-वृक्ष के लिंक और दिए गए ग्राफ़ की शाखाओं के अनुरूप हैं। इसलिए, मौलिक लूप मैट्रिक्स का क्रम होगा(b - n + 1) × b।
elements of fundamental loop matrix इन तीन मूल्यों में से एक होगा, +1, -1 और 0।
चयनित एफ-लूप के लिंक के लिए तत्व का मूल्य +1 होगा।
शेष लिंक और टहनियों के लिए तत्वों का मूल्य 0 होगा, जो चयनित एफ-लूप का हिस्सा नहीं हैं।
यदि चयनित एफ-लूप की टहनी की दिशा एफ-लूप लिंक वर्तमान के समान है, तो तत्व का मान +1 होगा।
यदि चयनित एफ-लूप की टहनी की दिशा एफ-लूप लिंक वर्तमान के विपरीत है, तो तत्व का मूल्य -1 होगा।
मौलिक लूप मैट्रिक्स खोजने की प्रक्रिया
दिए गए ग्राफ़ के मूल लूप मैट्रिक्स को खोजने के लिए इन चरणों का पालन करें।
दिए गए निर्देशित ग्राफ के एक पेड़ का चयन करें।
एक समय में एक लिंक को शामिल करके, हम एक एफ-लूप प्राप्त करेंगे। मौलिक लूप मैट्रिक्स की एक पंक्ति में इस एफ-लूप के अनुरूप तत्वों के मूल्यों को भरें।
सभी लिंक के लिए उपरोक्त चरण को दोहराएं।
उदाहरण
निम्नलिखित पेड़ पर एक नज़र डालें directed graph, जिसे घटना मैट्रिक्स के लिए माना जाता है।

उपरोक्त ट्री में तीन शाखाएँ शामिल हैं d, e & f। इसलिए, शाखाएँ, b & c, उपरोक्त ट्री के अनुरूप Co-Tree की लिंक होंगी। उपरोक्त ट्री के लिए एक समय में एक लिंक को शामिल करके, हम एक प्राप्त करेंगेf-loop। तो, तीन होंगेf-loops, क्योंकि तीन लिंक हैं। ये तीन एफ-लूप निम्न आकृति में दिखाए गए हैं।
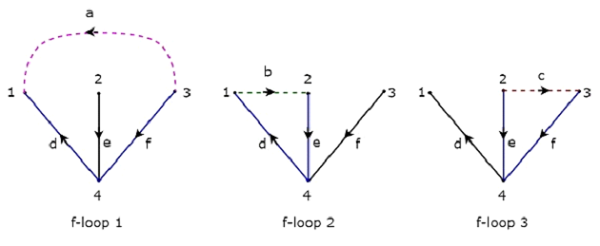
उपरोक्त आकृति में, शाखाओं, जिन्हें रंगीन रेखाओं के साथ दर्शाया जाता है, एफ-लूप बनाती हैं। हम प्रत्येक एफ-लूप से टाई-सेट मैट्रिक्स के पंक्ति वार तत्व मान प्राप्त करेंगे। ऐसाTieset matrix ऊपर माना पेड़ होगा
$$ B = \ start {bmatrix} 1 और 0 & -1 & 0 & -1 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \ _ अंत {bmatrix} $$
उपरोक्त मैट्रिक्स की पंक्तियाँ और स्तंभ दिए गए निर्देशित ग्राफ की लिंक और शाखाओं का प्रतिनिधित्व करते हैं। इस घटना मैट्रिक्स का क्रम 3 × 6 है।
number of Fundamental loop matricesएक निर्देशित ग्राफ, उस निर्देशित ग्राफ के पेड़ों की संख्या के बराबर होगा। क्योंकि, हर ट्री में एक फंडामेंटल लूप मैट्रिक्स होगा।
मौलिक कट-सेट मैट्रिक्स
मौलिक कटौती सेट या f-cut setशाखाओं की न्यूनतम संख्या है जो एक ग्राफ़ से इस तरह से हटा दी जाती है कि मूल ग्राफ़ दो अलग-अलग सबग्राफ बन जाएगा। एफ-कट सेट में ही होता हैone twigऔर एक या एक से अधिक लिंक। तो, एफ-कट सेट की संख्या टहनियों की संख्या के बराबर होगी।
Fundamental cut set matrix सी अक्षर के साथ प्रतिनिधित्व किया जाता है। यह मैट्रिक्स शाखा वोल्टेज और टहनी वोल्टेज के बीच संबंध देता है।
यदि 'एन' नोड्स हैं और 'बी' शाखाएं मौजूद हैं directed graph, तब दिए गए ग्राफ के एक चयनित ट्री में मौजूद टहनियों की संख्या n-1 होगी। तो, मूलभूत कट सेट मैट्रिक्स में 'n-1' पंक्तियाँ और 'b' कॉलम होंगे। यहां, पंक्तियां और स्तंभ चयनित पेड़ की टहनियों और दिए गए ग्राफ की शाखाओं के अनुरूप हैं। इसलिएorder मौलिक कट सेट मैट्रिक्स की होगी (n-1) × b।
elements of fundamental cut set matrix इन तीन मूल्यों में से एक होगा, +1, -1 और 0।
चयनित f-cutset की टहनी के लिए तत्व का मान +1 होगा।
शेष टहनियों और लिंक के लिए तत्वों का मूल्य 0 होगा, जो चयनित एफ-कटसेट का हिस्सा नहीं हैं।
यदि चयनित f-cut सेट की लिंक करंट की दिशा f-cutset twig current के समान है, तो तत्व का मान +1 होगा।
यदि चयनित f-cut सेट की लिंक करंट की दिशा f-cutset twig current के विपरीत है, तो तत्व का मान -1 होगा।
मौलिक कट-सेट मैट्रिक्स खोजने की प्रक्रिया
दिए गए ग्राफ़ के मूल कट सेट मैट्रिक्स को खोजने के लिए इन चरणों का पालन करें।
दिए गए ग्राफ़ के ट्री का चयन करें और बिंदीदार लाइनों के साथ लिंक का प्रतिनिधित्व करें।
एक समय में एक टहनी और आवश्यक लिंक को हटाकर, हम एक एफ-कट सेट प्राप्त करेंगे। मौलिक कट सेट मैट्रिक्स की एक पंक्ति में इस एफ-कट सेट के अनुरूप तत्वों के मूल्यों को भरें।
सभी टहनियों के लिए उपरोक्त चरण दोहराएं।
उदाहरण
उसी पर विचार करें directed graph , जो हमने घटना मैट्रिक्स के अनुभाग में चर्चा की। टहनियों के रूप में इस निर्देशित ग्राफ की शाखाओं d, e & f का चयन करें। तो, इस निर्देशित ग्राफ की शेष शाखाएं, बी और सी लिंक होंगी।
twigs डी, ई एंड एफ को ठोस लाइनों के साथ दर्शाया गया है और links ए, बी और सी को निम्न आकृति में बिंदीदार रेखाओं के साथ दर्शाया गया है।
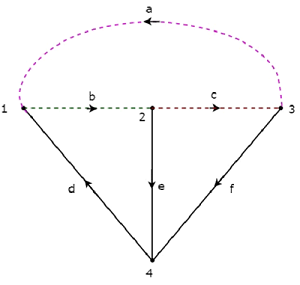
एक समय में एक टहनी और आवश्यक लिंक को हटाकर, हम एक एफ-कट सेट प्राप्त करेंगे। तो, तीन एफ-कट सेट होंगे, क्योंकि तीन टहनियाँ हैं। इन तीनf-cut sets निम्नलिखित आकृति में दिखाए गए हैं।

हमारे पास सी 1 , सी 2 और सी 3 के ट्विग और लिंक के एक सेट को हटाकर तीन एफ-कट सेट होंगे । हम प्रत्येक f-cut सेट से मूलभूत कट सेट मैट्रिक्स के पंक्ति वार तत्व मान प्राप्त करेंगे। ऐसाfundamental cut set matrix ऊपर माना पेड़ होगा
$$ C = \ start {bmatrix} 1 और -1 & 0 & 1 & 0 & \ _ 0 & -1 और 1 & 1 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 & अंत {bmatrix} $$
उपरोक्त मैट्रिक्स की पंक्तियाँ और स्तंभ दिए गए निर्देशित ग्राफ की टहनियों और शाखाओं का प्रतिनिधित्व करते हैं। इस मूलभूत कट सेट मैट्रिक्स का क्रम 3 × 6 है।
number of Fundamental cut set matricesएक निर्देशित ग्राफ, उस निर्देशित ग्राफ के पेड़ों की संख्या के बराबर होगा। क्योंकि, हर ट्री में एक फंडामेंटल कट सेट मैट्रिक्स होगा।