अधिकतम शक्ति हस्तांतरण प्रमेय
भार द्वारा प्राप्त शक्ति की मात्रा विद्युत और इलेक्ट्रॉनिक अनुप्रयोगों में एक महत्वपूर्ण पैरामीटर है। डीसी सर्किट में, हम आर एल ओम के प्रतिरोध वाले प्रतिरोध के साथ लोड का प्रतिनिधित्व कर सकते हैं । इसी तरह, एसी सर्किट में, हम जेड एल ओम के प्रतिबाधा वाले जटिल भार के साथ इसका प्रतिनिधित्व कर सकते हैं ।
Maximum power transfer theorem बताता है कि डीसी वोल्टेज स्रोत चर लोड रोकनेवाला को अधिकतम शक्ति तभी प्रदान करेगा जब लोड प्रतिरोध स्रोत प्रतिरोध के बराबर हो।
इसी तरह, Maximum power transfer theorem बताता है कि एसी वोल्टेज स्रोत केवल वैरिएबल कॉम्प्लेक्स लोड को अधिकतम शक्ति प्रदान करेगा, जब लोड प्रतिबाधा स्रोत प्रतिबाधा के जटिल संयुग्म के बराबर हो।
इस अध्याय में, डीसी सर्किट के लिए अधिकतम शक्ति हस्तांतरण प्रमेय के बारे में चर्चा करते हैं।
अधिकतम शक्ति हस्तांतरण प्रमेय का प्रमाण
किसी भी दो टर्मिनल लीनियर नेटवर्क या सर्किट को वेरिएबल लोड रेसिस्टर के बाईं ओर स्थित करें, जिसमें एक एल्विन के समकक्ष सर्किट के साथ R L ओम का प्रतिरोध हो । हम जानते हैं कि थेवेन के समतुल्य सर्किट एक व्यावहारिक वोल्टेज स्रोत के समान है।
यह अवधारणा निम्नलिखित आंकड़ों में सचित्र है।
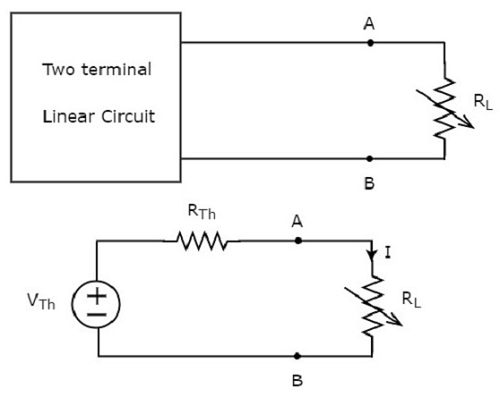
लोड प्रतिरोधक में विघटित शक्ति की मात्रा है
$ $ P_L = I ^ 2 R_L $ $
उपर्युक्त समीकरण में $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $।
$ $ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$
$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Equation 1
अधिकतम पावर ट्रांसफर के लिए शर्त
अधिकतम या न्यूनतम के लिए, पहला व्युत्पन्न शून्य होगा। इसलिए, R L के संबंध में समीकरण 1 को अलग करें और इसे शून्य के बराबर करें।
$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ 1 बार - R_L \ गुना 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $ $
$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $ $
$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = $ $
$$ \ Rightarrow (R_ {Th} - R_L) = 0 $ $
$$ \ Rightarrow R_ {Th} = R_L \: या \: R_L = R_ {Th} $ $
इसलिए condition for maximum powerलोड भर में अपव्यय $ R_L = R_ {Th} $ है। इसका मतलब है, यदि लोड प्रतिरोध का मान स्रोत प्रतिरोध के सिद्धांत के बराबर है, थ्वेनिन का प्रतिरोध, तो लोड भर में फैली शक्ति अधिकतम मूल्य की होगी।
अधिकतम पावर ट्रांसफर का मूल्य
$ $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ समीकरण 1 में।
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$
$ $ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \ _: \ _ R_ {L} = R_ {Th} $ $
इसलिए maximum amount of power भार को हस्तांतरित किया जाता है
$ $ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $ $
अधिकतम बिजली हस्तांतरण की क्षमता
हम निम्नलिखित सूत्र का उपयोग करके अधिकतम शक्ति हस्तांतरण, $ \ eta_ {Max} $ की दक्षता की गणना कर सकते हैं।
$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Equation 2
कहाँ पे,
$ P_ {L, Max} $ लोड को हस्तांतरित शक्ति की अधिकतम राशि है।
$ P_S $ स्रोत द्वारा उत्पन्न शक्ति की राशि है।
amount of power generated स्रोत से है
$ $ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$
$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \ _ से: \ _ R_ {L} = R_ {Th} $ $
उपर्युक्त समीकरण में $ I = \ frac {V_ {Th}} {2 R_ {Th}} $।
$ $ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $ $
$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $ $
$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th} $$
समीकरण 2 में $ P_ {L, Max} $ और $ P_S $ के मूल्यों को प्रतिस्थापित करें।
$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} {} 2R_ {गु}} \ rgroup} $$
$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $ $
हम अधिकतम बिजली हस्तांतरण की दक्षता का प्रतिनिधित्व कर सकते हैं percentage निम्नानुसार है -
$$ \% \ eta_ {Max} = \ eta_ {Max} \ 100 बार $ \ $ $
$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ गुना 100 \% $ $
$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $ $
इसलिए, अधिकतम बिजली हस्तांतरण की दक्षता है 50 %।
उदाहरण
खोजो maximum powerजिसे निम्न चित्र में दिखाए गए सर्किट के लोड रेसिस्टर R L तक पहुंचाया जा सकता है ।
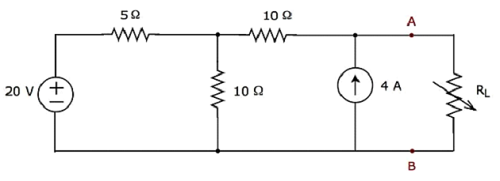
Step 1- Thevenin के प्रमेय अध्याय में, हमने Thevenin के समतुल्य परिपथ की गणना बायीं ओर के टर्मिनलों A & B से की है। अब हम इस परिपथ का उपयोग कर सकते हैं। इसे निम्नलिखित आकृति में दिखाया गया है।
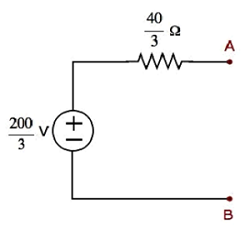
यहाँ, थेवेनिन के वोल्टेज $ V_ {Th} = \ frac {200} {3} V $ और थेविन के प्रतिरोध $ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2- सर्किट के उस हिस्से को बदलें, जो ऊपर दिए गए थेविन के समकक्ष सर्किट के साथ दिए गए सर्किट के टर्मिनलों ए एंड बी के बाईं ओर है। परिणामी सर्किट आरेख निम्न आकृति में दिखाया गया है।

Step 3- हम निम्नलिखित सूत्र का उपयोग करके अधिकतम शक्ति पा सकते हैं जो लोड रोकनेवाला, आर एल तक पहुंचाई जाएगी।
$ $ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th} $$
उपर्युक्त सूत्र में $ V_ {Th} = \ frac {200} {3} V $ और $ R_ {Th} = \ frac {40} {3} \ Omega $।
$ $ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$
$ $ P_ {L, Max} = \ frac {250} {3} W $ $
इसलिए maximum power जो दिए गए सर्किट के लोड रेसिस्टर RL को दिया जाएगा, वह $ \ mathbf {\ frac {250} {{}} $ है W