नेटवर्क थ्योरी - नेटवर्क टोपोलॉजी
नेटवर्क टोपोलॉजी विद्युत सर्किट का एक चित्रमय प्रतिनिधित्व है। यह जटिल इलेक्ट्रिक सर्किटों का विश्लेषण करके उन्हें नेटवर्क ग्राफ में परिवर्तित करने के लिए उपयोगी है। नेटवर्क टोपोलॉजी को भी कहा जाता हैGraph theory।
नेटवर्क टोपोलॉजी की बुनियादी शब्दावली
अब, इस नेटवर्क टोपोलॉजी में शामिल बुनियादी शब्दावली के बारे में चर्चा करते हैं।
ग्राफ़
नेटवर्क ग्राफ बस के रूप में कहा जाता है graph। इसमें शाखाओं द्वारा जुड़े नोड्स का एक सेट होता है। रेखांकन में, एक नोड दो या दो से अधिक शाखाओं का एक सामान्य बिंदु है। कभी-कभी, केवल एक ही शाखा नोड से जुड़ सकती है। एक शाखा एक लाइन खंड है जो दो नोड्स को जोड़ता है।
किसी भी विद्युत सर्किट या नेटवर्क को इसके समकक्ष में परिवर्तित किया जा सकता है graphशॉर्ट सर्किट के साथ निष्क्रिय तत्वों और वोल्टेज स्रोतों की जगह और खुले सर्किट के साथ वर्तमान स्रोत। इसका मतलब है, ग्राफ में लाइन सेगमेंट या तो निष्क्रिय तत्वों या विद्युत सर्किट के वोल्टेज स्रोतों के अनुरूप शाखाओं का प्रतिनिधित्व करते हैं।
उदाहरण
आइए हम निम्नलिखित पर विचार करें electric circuit।
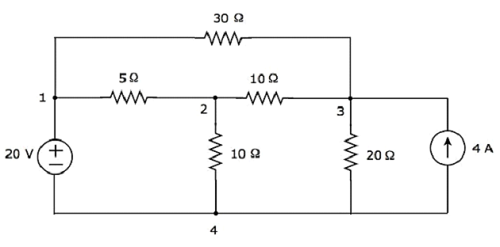
उपरोक्त सर्किट में, हैं four principal nodes और उन पर 1, 2, 3 और 4 का लेबल लगाया जाता है seven branches उपरोक्त सर्किट में, जिसके बीच में एक शाखा में 20 वी वोल्टेज स्रोत होता है, दूसरी शाखा में एक 4 ए वर्तमान स्रोत होता है और शेष पांच शाखाओं में क्रमशः 30 Ω, 5 Ω, 10 among, 10 Ω और 20 contain के प्रतिरोध वाले प्रतिरोध होते हैं।
एक समकक्ष graph उपरोक्त विद्युत सर्किट के अनुरूप निम्नलिखित आकृति में दिखाया गया है।
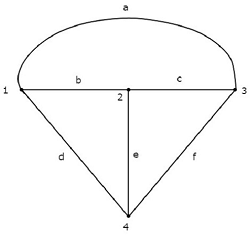
उपरोक्त ग्राफ में, हैं four nodesऔर उन पर क्रमशः 1, 2, 3 और 4 का लेबल लगाया जाता है। ये विद्युत परिपथ में मुख्य नोड्स के समान हैं। वहांsix branches उपरोक्त ग्राफ में और उन पर क्रमशः ए, बी, सी, डी, ई और एफ के साथ लेबल लगाए गए हैं।
इस मामले में, हमें मिला one branch less ग्राफ में क्योंकि विद्युत परिपथ को उसके समतुल्य ग्राफ में परिवर्तित करते हुए 4 A वर्तमान स्रोत को ओपन सर्किट बनाया जाता है।
इस उदाहरण से, हम निम्नलिखित बिंदुओं का निष्कर्ष निकाल सकते हैं -
number of nodes एक ग्राफ में मौजूद एक इलेक्ट्रिक सर्किट में मौजूद प्रमुख नोड्स के बराबर होगा।
number of branches एक ग्राफ में मौजूद विद्युत परिपथ में मौजूद शाखाओं की संख्या की तुलना में कम या बराबर होगी।
रेखांकन के प्रकार
निम्नलिखित रेखांकन के प्रकार हैं -
- जुड़ा हुआ ग्राफ
- असंबद्ध ग्राफ
- निर्देशित आलेख
- अप्रत्यक्ष ग्राफ़
अब, एक-एक करके इन ग्राफ पर चर्चा करते हैं।
जुड़ा हुआ ग्राफ
यदि ग्राफ़ के किसी भी दो नोड्स के बीच कम से कम एक शाखा मौजूद है, तो इसे ए कहा जाता है connected graph। इसका मतलब है, जुड़े हुए ग्राफ में प्रत्येक नोड में एक या अधिक शाखाएँ होंगी जो इससे जुड़ी हैं। तो, कोई नोड पृथक या पृथक के रूप में प्रस्तुत नहीं करेगा।
पिछले उदाहरण में दिखाया गया ग्राफ एक है connected graph। यहां, सभी नोड्स तीन शाखाओं द्वारा जुड़े हुए हैं।
असंबद्ध ग्राफ
यदि ग्राफ़ में कम से कम एक नोड मौजूद है जो एकल शाखा द्वारा भी असंबद्ध रहता है, तो इसे ए कहा जाता है unconnected graph। तो, एक असंबद्ध ग्राफ में एक या अधिक पृथक नोड्स होंगे।
निम्नलिखित आकृति में दिखाए गए ग्राफ पर विचार करें।
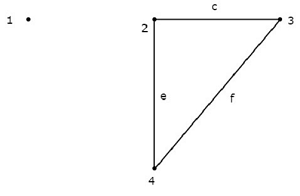
इस ग्राफ में, नोड्स 2, 3 और 4 प्रत्येक दो शाखाओं द्वारा जुड़े हुए हैं। लेकिन, एक भी शाखा से जुड़ा नहीं हैnode 1। तो, नोड 1 बन जाता हैisolated node। इसलिए, उपरोक्त ग्राफ एक हैunconnected graph।
निर्देशित आलेख
यदि किसी ग्राफ की सभी शाखाओं को तीरों से दर्शाया जाता है, तो उस ग्राफ को एक कहा जाता है directed graph। ये तीर प्रत्येक शाखा में वर्तमान प्रवाह की दिशा को इंगित करते हैं। इसलिए, इस ग्राफ को भी कहा जाता हैoriented graph।
निम्नलिखित आकृति में दिखाए गए ग्राफ पर विचार करें।
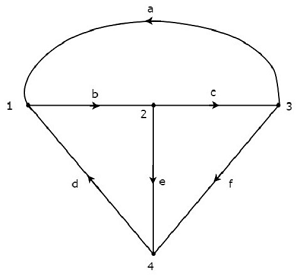
उपरोक्त ग्राफ में, वर्तमान प्रवाह की दिशा को प्रत्येक शाखा में एक तीर के साथ दर्शाया गया है। इसलिए, यह एक हैdirected graph।
अप्रत्यक्ष ग्राफ़
यदि किसी ग्राफ की शाखाओं को तीरों के साथ नहीं दर्शाया जाता है, तो उस ग्राफ को एक कहा जाता है undirected graph। चूंकि, वर्तमान प्रवाह की कोई दिशा नहीं है, इसलिए इस ग्राफ को ए भी कहा जाता हैunoriented graph।
इस अध्याय के पहले उदाहरण में दिखाया गया ग्राफ एक है unoriented graph, क्योंकि उस ग्राफ की शाखाओं पर कोई तीर नहीं हैं।
सबग्राफ और इसके प्रकार
ग्राफ के एक भाग को एक कहा जाता है subgraph। हम दिए गए ग्राफ के कुछ नोड्स और / या शाखाओं को हटाकर सबग्राफ प्राप्त करते हैं। इसलिए, सबग्राफ की शाखाओं और / या नोड्स की संख्या मूल ग्राफ से कम होगी। इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि एक सबग्राफ एक ग्राफ का सबसेट है।
निम्नलिखित हैं two types सबग्राफ के।
- Tree
- Co-Tree
पेड़
ट्री एक दिए गए ग्राफ का एक जुड़ा हुआ सबग्राफ है, जिसमें एक ग्राफ के सभी नोड्स होते हैं। लेकिन, उस सबग्राफ में कोई लूप नहीं होना चाहिए। एक पेड़ की शाखाओं को कहा जाता हैtwigs।
निम्नलिखित को धयान मे रखते हुए connected subgraph ग्राफ, जो इस अध्याय की शुरुआत के उदाहरण में दिखाया गया है।
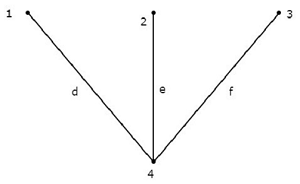
इस जुड़े सबग्राफ में दिए गए ग्राफ़ के सभी चार नोड्स होते हैं और कोई लूप नहीं होता है। इसलिए, यह एक हैTree।
इस ट्री में दिए गए ग्राफ की छह शाखाओं में से केवल तीन शाखाएँ हैं। क्योंकि, अगर हम ग्राफ की शेष शाखाओं की एक भी शाखा पर विचार करते हैं, तो उपरोक्त जुड़े हुए सबग्राफ में एक लूप होगा। फिर, परिणामी जुड़ा उपसमूह ट्री नहीं होगा।
उपरोक्त वृक्ष से, हम यह निष्कर्ष निकाल सकते हैं कि number of branches एक पेड़ में मौजूद हैं कि बराबर होना चाहिए n - 1 जहाँ 'n' दिए गए ग्राफ के नोड्स की संख्या है।
सह-ट्री
को-ट्री एक सबग्राफ है, जो उन शाखाओं के साथ बनता है जिन्हें ट्री बनाते समय हटा दिया जाता है। इसलिए, इसे कहा जाता हैComplementएक पेड़ की। प्रत्येक ट्री के लिए, एक सह-ट्री होगा और इसकी शाखाओं को कहा जाता हैlinksया राग। सामान्य तौर पर, लिंक को बिंदीदार रेखाओं के साथ दर्शाया जाता है।
Co-Tree उपरोक्त ट्री से संबंधित निम्नलिखित आकृति में दिखाया गया है।
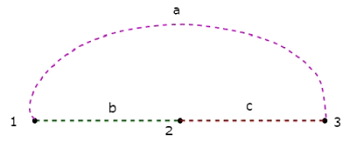
इस को-ट्री में दिए गए ग्राफ के चार नोड्स के बजाय केवल तीन नोड्स हैं, क्योंकि नोड 4 को ऊपर के ट्री से अलग किया गया है। इसलिए, को-ट्री को कनेक्टेड सबग्राफ की आवश्यकता नहीं है। इस सह-वृक्ष की तीन शाखाएँ हैं और वे एक लूप बनाते हैं।
number of branchesसह-वृक्ष में मौजूद हैं, किसी दिए गए ग्राफ की शाखाओं की संख्या और टहनियों की संख्या के बीच के अंतर के बराबर होंगे। गणितीय रूप से, इसे लिखा जा सकता है
$ $ एल = बी - (एन - 1) $ $
$ $ एल = बी - एन + 1 $ $
कहाँ पे,
- l लिंक की संख्या है।
- b किसी दिए गए ग्राफ में मौजूद शाखाओं की संख्या है।
- n किसी दिए गए ग्राफ़ में मौजूद नोड्स की संख्या है।
यदि हम एक ट्री और इसके संगत को-ट्री को मिलाते हैं, तो हम इसे प्राप्त करेंगे original graph जैसा की नीचे दिखाया गया।
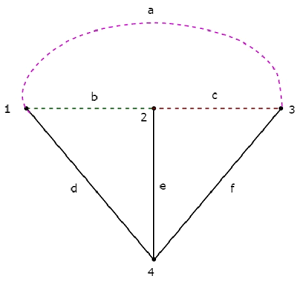
वृक्ष की शाखाएँ d, e & f को ठोस रेखाओं से दर्शाया गया है। सह-वृक्ष शाखाएं ए, बी और सी को धराशायी लाइनों के साथ दर्शाया गया है।