नेटवर्क थ्योरी - एसी सर्किट की प्रतिक्रिया
पिछले अध्याय में, हमने डीसी सर्किट की क्षणिक प्रतिक्रिया और स्थिर राज्य प्रतिक्रिया पर चर्चा की। इस अध्याय में, आइए चर्चा करते हैंresponse of AC circuit। क्षणिक प्रतिक्रिया और स्थिर राज्य प्रतिक्रिया दोनों की अवधारणाएं, जिनके बारे में हमने पिछले अध्याय में चर्चा की थी, यहाँ भी उपयोगी होगी।
श्रृंखला आरएल सर्किट की प्रतिक्रिया खोजना
निम्नलिखित को धयान मे रखते हुए series RL circuit आरेख।

उपरोक्त सर्किट में, switch रखा गया था openअप करने के लिए t = 0 और यह बंद हो गया पर t = 0 । तो, V m वोल्ट के पीक वोल्टेज वाले AC वोल्टेज स्रोत श्रृंखला RL सर्किट से इस तत्काल तक जुड़ा नहीं है। इसलिए, वहाँ हैno initial current प्रारंभ करनेवाला के माध्यम से बहती है।
सर्किट आरेख, जब switch में है closed स्थिति, निम्न आकृति में दिखाई गई है।
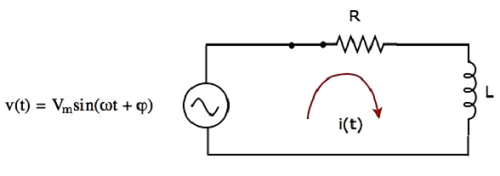
अब, वर्तमान मैं (टी) , पूरे सर्किट में बहती है के बाद से एसी वोल्टेज स्रोत के पीक वोल्टेज होने वी मीटर वोल्ट श्रृंखला आर एल सर्किट से जुड़ा है।
हम जानते हैं कि उपरोक्त सर्किट से बहने वाली वर्तमान i (t) में दो पद होंगे, एक जो क्षणिक भाग का प्रतिनिधित्व करता है और दूसरा शब्द स्थिर अवस्था का प्रतिनिधित्व करता है।
गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1
कहाँ पे,
$ i_ {Tr} (t) $ सर्किट के माध्यम से बहने वाली वर्तमान की क्षणिक प्रतिक्रिया है।
$ i_ {ss} (t) $ सर्किट के माध्यम से बहने वाली वर्तमान स्थिति की स्थिर स्थिति है।
पिछले अध्याय में, हमें श्रृंखला आरएल सर्किट के माध्यम से बहने वाले वर्तमान की क्षणिक प्रतिक्रिया मिली। यह $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ के रूप में है।
$ $ I_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ समीकरण 1 में।
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $Equation 2
स्थिर राज्य की गणना
यदि एक साइनसॉइडल सिग्नल को रैखिक इलेक्ट्रिक सर्किट के इनपुट के रूप में लागू किया जाता है, तो यह एक स्थिर राज्य आउटपुट का उत्पादन करता है, जो कि एक भी है sinusoidal signal। इनपुट और आउटपुट दोनों साइनसॉइडल सिग्नल एक ही आवृत्ति वाले होंगे, लेकिन विभिन्न आयाम और चरण कोण।
हम एक विद्युत सर्किट की स्थिर स्थिति प्रतिक्रिया की गणना कर सकते हैं, जब यह एक साइनसॉइडल वोल्टेज स्रोत का उपयोग करके उत्साहित होता है Laplace Transform approach।
एस-डोमेन सर्किट आरेख, जब switch में है closed स्थिति, निम्न आकृति में दिखाई गई है।
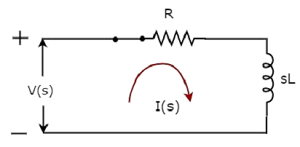
उपरोक्त सर्किट में, सभी मात्राओं और मापदंडों का प्रतिनिधित्व किया जाता है s-domain। ये टाइम-डोमेन मात्रा और मापदंडों के लाप्लास रूपांतर हैं।
Transfer function उपरोक्त सर्किट का है
$ $ H (s) = \ frac {I (s)} {V (s)} $ $
$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $ $
$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $ $
उपरोक्त समीकरण में $ s = j \ omega $ को स्थान दें।
$$ H (j \ _ omega) = \ frac {1} {R + j \ omega L} $$
Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ है
$ $ | एच (j \ omega) = \ frac {1} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2} L ^ 2} $ $
Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ है
$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$
हमें मिलेगा steady state current $ i_ {ss} (t) $ निम्नलिखित दो चरण करके -
इनपुट साइनसोइडल वोल्टेज के शिखर वोल्टेज और $ H (j \ omega) $ के परिमाण को गुणा करें।
इनपुट साइनसॉइडल वोल्टेज और $ H (j \ omega) $ के चरण कोणों को जोड़ें।
steady state current $ i_ {ss} (t) $ होगा
$ $ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $ $
समीकरण 2 में $ i_ {ss} (t) $ के मूल्य को प्रतिस्थापित करें।
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 ^ ^ 2}} पाप \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3
हम जानते हैं कि सर्किट में कोई प्रारंभिक प्रवाह नहीं है। इसलिए, स्थिरांक का मान ज्ञात करने के लिए, समीकरण 3 में t = 0 और i (t) = 0 को प्रतिस्थापित करें ।
$ $ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L = 2}} sin \ lgroup \ _ ओमेगा (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} / lgroup \ frac {\ _ ओमेगा एल} {आर} \ rgroup \ rgroup $ $
$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} / lgroup \ frac {\ _ omega L} {R} \ rgroup \ rgroup $$
समीकरण 3 में K के मान को प्रतिस्थापित करें ।
$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup / frac {\ _ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4
समीकरण 4 श्रृंखला आरएल सर्किट के माध्यम से बहने वाले वर्तमान का प्रतिनिधित्व करता है, जब यह एक साइनसोइडल वोल्टेज स्रोत द्वारा उत्साहित होता है। इसकी दो शर्तें हैं। पहले और दूसरे शब्द क्रमशः क्षणिक प्रतिक्रिया और वर्तमान की स्थिर राज्य प्रतिक्रिया का प्रतिनिधित्व करते हैं।
हम कर सकते हैं neglect the first termसमीकरण 4 क्योंकि इसका मूल्य एक से बहुत कम होगा। तो, सर्किट के माध्यम से बहने वाला परिणामी प्रवाह होगा
$ $ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ _ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {1} \ lgroup \ _ frac {\ _ omega L} {R} \ rgroup \ rgroup $$
इसमें केवल शामिल है steady state term। इसलिए, हम केवल एसी सर्किट की स्थिर स्थिति प्रतिक्रिया और इसके बारे में क्षणिक प्रतिक्रिया की उपेक्षा कर सकते हैं।