इलेक्ट्रिकल क्वांटिटी डिवीजन सिद्धांत
इस अध्याय में, हम विद्युत मात्रा के निम्नलिखित दो विभाजन सिद्धांतों के बारे में चर्चा करते हैं।
- वर्तमान डिवीजन सिद्धांत
- वोल्टेज डिवीजन सिद्धांत
वर्तमान डिवीजन सिद्धांत
जब दो या दो से अधिक निष्क्रिय तत्व समानांतर में जुड़े होते हैं, तो प्रत्येक तत्व से प्रवाहित होने वाली धारा की मात्रा हो जाती है divided (साझा) नोड में प्रवेश करने वाले वर्तमान से आपस में।
निम्नलिखित को धयान मे रखते हुए circuit diagram।
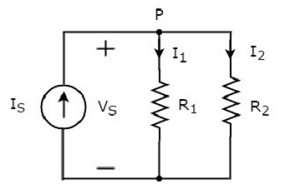
उपरोक्त सर्किट आरेख में एक इनपुट वर्तमान स्रोत होता है IS दो प्रतिरोधों के साथ समानांतर में R1 तथा R2। प्रत्येक तत्व में वोल्टेज हैVS। प्रतिरोधों के माध्यम से बहने वाली धाराएंR1 तथा R2 कर रहे हैं I1 तथा I2 क्रमशः।
KCL equation नोड पर P होगा
$ $ I_S = I_1 + I_2 $ $
उपर्युक्त समीकरण में $ I_1 = \ frac {V_S} {R_1} $ और $ I_2 = \ frac {V_S} {R_2} $।
$ $ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} / Agroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
$ I_1 = \ frac {V_S} {R_1} $ में V S के मूल्य को प्रतिस्थापित करें ।
$ $ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
$ I_2 = \ frac {V_S} {R_2} $ में V S के मूल्य को प्रतिस्थापित करें ।
$ $ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
I 1 और I 2 के समीकरणों से , हम यह सामान्य कर सकते हैं कि किसी भी निष्क्रिय तत्व के माध्यम से बहने वाले वर्तमान को निम्न सूत्र का उपयोग करके पाया जा सकता है।
$ $ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgert $$
इस रूप में जाना जाता है current division principle और यह तब लागू होता है, जब दो या अधिक निष्क्रिय तत्व समानांतर में जुड़े होते हैं और केवल एक वर्तमान नोड में प्रवेश करता है।
कहाँ पे,
I N , N वें शाखा के निष्क्रिय तत्व से प्रवाहित होने वाली धारा है ।
I S इनपुट करंट है, जो नोड में प्रवेश करता है।
जेड 1 , जेड 2 ,…, जेड एन क्रमशः 1 सेंट शाखा, 2 एनडी शाखा,…, एन वें शाखा के प्रतिबाधा हैं।
वोल्टेज डिवीजन सिद्धांत
जब दो या अधिक निष्क्रिय तत्व श्रृंखला में जुड़े होते हैं, तो प्रत्येक तत्व में मौजूद वोल्टेज की मात्रा मिलती है divided (साझा) उस पूरे संयोजन में उपलब्ध वोल्टेज से आपस में।
निम्नलिखित को धयान मे रखते हुए circuit diagram।
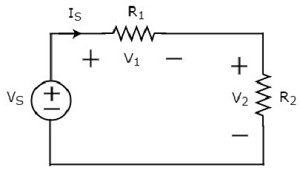
उपरोक्त सर्किट आरेख में एक वोल्टेज स्रोत होता है, दो प्रतिरोधों आर 1 और आर 2 के साथ श्रृंखला में वी एस । इन तत्वों के माध्यम से बहने वाली वर्तमान I S है । प्रतिरोध आर 1 और आर 2 में वोल्टेज क्रमशः वी 1 और वी 2 हैं।
KVL equation चारों ओर लूप होगा
$ $ V_S = V_1 + V_2 $$
स्थानापन्न वी 1 = मैं एस आर 1 और वी 2 = मैं एस आर 2 उपर्युक्त समीकरण में
$ $ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $ $
$ $ I_S = \ frac {V_S} {R_1 + R_2} $ $
V 1 = I S R 1 में I S का मान रखें ।
$ $ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1% =
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
V 2 = I S R 2 में I S का मान रखें ।
$ $ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2% $
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
वी 1 और वी 2 के समीकरणों से , हम सामान्य कर सकते हैं कि किसी भी निष्क्रिय तत्व के पार वोल्टेज निम्नलिखित सूत्र का उपयोग करके पाया जा सकता है।
$ $ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
इस रूप में जाना जाता है voltage division principle और यह तब लागू होता है, जब दो या दो से अधिक निष्क्रिय तत्व श्रृंखला में जुड़े होते हैं और पूरे संयोजन में केवल एक वोल्टेज उपलब्ध होता है।
कहाँ पे,
V N , N वें निष्क्रिय तत्व में वोल्टेज है।
वी एस इनपुट वोल्टेज है, जो श्रृंखला निष्क्रिय तत्वों के पूरे संयोजन में मौजूद है।
जेड 1 , जेड 2 ,…, जेड 3 क्रमशः 1 सेंट निष्क्रिय तत्व, 2 एन डी निष्क्रिय तत्व,…, एन वें निष्क्रिय तत्व के प्रतिबाधा हैं।