नेटवर्क थ्योरी - मेष विश्लेषण
मेष विश्लेषण में, हम प्रत्येक जाल के माध्यम से बहने वाली धाराओं पर विचार करेंगे। इसलिए, मेष विश्लेषण भी कहा जाता हैMesh-current method।
ए branchएक ऐसा मार्ग है जो दो नोड्स को जोड़ता है और इसमें एक सर्किट तत्व होता है। यदि एक शाखा केवल एक जाल से संबंधित है, तो शाखा धारा मेष वर्तमान के बराबर होगी।
यदि एक शाखा दो मेषों के लिए आम है, तो शाखा प्रवाह दो मेष धाराओं के योग (या अंतर) के बराबर होगा, जब वे एक ही (या विपरीत) दिशा में होते हैं।
मेष विश्लेषण की प्रक्रिया
मेष विश्लेषण का उपयोग करके किसी भी विद्युत नेटवर्क या सर्किट को हल करते समय इन चरणों का पालन करें।
Step 1 - पहचानें meshes और घड़ी की दिशा या विरोधी घड़ी की दिशा में जाल धाराओं को लेबल करें।
Step 2 - मेष धाराओं के संदर्भ में प्रत्येक तत्व के माध्यम से बहने वाली वर्तमान की मात्रा का निरीक्षण करें।
Step 3 - लिखो mesh equationsसभी जालों को। मेष समीकरण पहले KVL और फिर ओम के नियम को लागू करके प्राप्त किया जाता है।
Step 4 - चरण 3 में प्राप्त मेष समीकरणों को हल करने के क्रम में mesh currents।
अब, हम किसी भी तत्व के माध्यम से बहने वाले वर्तमान और किसी भी तत्व में वोल्टेज को पा सकते हैं, जो कि जाल धाराओं का उपयोग करके दिए गए नेटवर्क में मौजूद है।
उदाहरण
उपयोग करने वाले 30 voltage अवरोधक के पार वोल्टेज का पता लगाएं Mesh analysis।
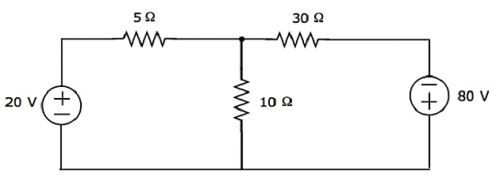
Step 1- उपरोक्त सर्किट में दो मेष हैं। mesh currentsI 1 और I 2 को दक्षिणावर्त दिशा में माना जाता है। इन जाली धाराओं को निम्न आकृति में दिखाया गया है।
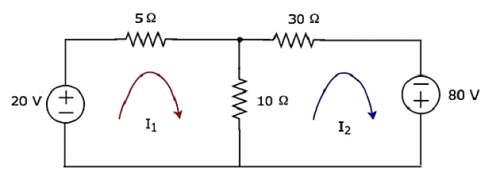
Step 2- मेष वर्तमान I 1 20 V वोल्टेज स्रोत और 5 current अवरोधक के माध्यम से बहता है। इसी तरह, मेष वर्तमान I 2 30 and रोकनेवाला और -80 वी वोल्टेज स्रोत से बहता है। लेकिन, दो मेष धाराओं, I 1 और I 2 का अंतर, 10, अवरोधक से होकर बहता है, क्योंकि यह दो मेषों की सामान्य शाखा है।
Step 3 - इस मामले में, हम प्राप्त करेंगे two mesh equationsचूंकि दिए गए सर्किट में दो मेष हैं। जब हम मेष समीकरण लिखते हैं, तो सर्किट के अन्य सभी मेष धाराओं की तुलना में उस विशेष मेष के मेष वर्तमान को मान लें।
mesh equation पहला जाल है
$ $ 20 - 5I_1 -10 (I_1 - I_2) = 0 $ $
$$ \ Rightarrow 20 - 15I_1 + 10I_2 = 0 $ $
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $ $
उपरोक्त समीकरण को 5 से विभाजित करें।
$ $ 2I_2 = 3I_1 - 4 $ $
उपरोक्त समीकरण को 2 से गुणा करें।
$ 4I_2 = 6I_1 - 8 $ Equation 1
mesh equation दूसरी जाली है
$ $ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $ $
उपरोक्त समीकरण को 10 से विभाजित करें।
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $ $
$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $ $
$ 4I_2 = I_1 + 8 $ Equation 2
Step 4- समीकरण 1 और समीकरण 2 हल करके मेष धाराओं I 1 और I 2 का पता लगाना ।
समीकरण 1 और समीकरण 2 के बाएँ हाथ की शर्तें समान हैं। इसलिए, समीकरण 1 और समीकरण 2 के दाईं ओर के शब्दों को समान करें । I 1 का मान ज्ञात करें ।
$ $ 6I_1 - 8 = I_1 + 8 $ $
$$ \ Rightarrow 5I_1 = 16 $ $
$$ \ Rightarrow I_1 = \ frac {16} {5} एक $ $
समीकरण 2 में स्थानापन्न I 1 मान।
$ $ 4I_2 = \ frac {16} {5} + 8 $ $
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $ $
$$ \ Rightarrow I_2 = \ frac {14} {5} एक $ $
तो, हम जाल धाराओं मिल गया मैं 1 और मैं 2 के रूप में $ \ mathbf {\ frac {16} {5}} $A और $ \ mathbf {\ frac {14} {5}} $ A क्रमशः।
Step 5- 30 or अवरोधक के माध्यम से बहने वाली धारा कुछ नहीं है, लेकिन मेष वर्तमान I 2 और यह $ \ frac {14} {5} $ A. के बराबर है। अब, हम ओम के नियम का उपयोग करके 30 or अवरोधक के पार वोल्टेज पा सकते हैं।
$ $ V_ {30 \ Omega} = I_2 R $ $
उपरोक्त समीकरण में I 2 और R के मानों को बदलें।
$ $ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $ $
$$ \ Rightarrow V_ {30 \ Omega} = 84V $ $
इसलिए, दिए गए सर्किट के 30 30 रोकने वाला वोल्टेज है 84 V।
Note 1- उपरोक्त उदाहरण से, हम यह निष्कर्ष निकाल सकते हैं कि हमें 'm' मेष समीकरणों को हल करना है, यदि विद्युत सर्किट में 'm' मेष हैं। इसलिए हम मेष विश्लेषण का चयन कर सकते हैं, जब किसी विद्युत सर्किट के मूल नोड्स (संदर्भ नोड को छोड़कर) की संख्या से कम मेषों की संख्या होती है।
Note 2 - हम या तो नोडल विश्लेषण या मेष विश्लेषण का चयन कर सकते हैं, जब किसी भी विद्युत सर्किट में मेषों की संख्या प्रिंसिपल नोड्स (संदर्भ नोड को छोड़कर) की संख्या के बराबर होती है।