नेटवर्क थ्योरी - डीसी सर्किट का जवाब
यदि किसी इनपुट के लिए इलेक्ट्रिक सर्किट का आउटपुट समय के साथ बदलता रहता है, तो इसे कहा जाता है time response। समय प्रतिक्रिया में दो भाग होते हैं।
- अस्थायी प्रतिसाद
- स्थिर राज्य प्रतिक्रिया
इस अध्याय में, पहले इन दो प्रतिक्रियाओं के बारे में चर्चा करते हैं और फिर एक श्रृंखला आरएल सर्किट में इन दो प्रतिक्रियाओं का निरीक्षण करते हैं, जब यह डीसी वोल्टेज स्रोत द्वारा उत्साहित होता है।
अस्थायी प्रतिसाद
इलेक्ट्रिक सर्किट में इनपुट लगाने के बाद, आउटपुट को स्थिर स्थिति तक पहुंचने में निश्चित समय लगता है। इसलिए, आउटपुट क्षणिक स्थिति में होगा जब तक कि यह स्थिर स्थिति में नहीं जाता है। इसलिए, क्षणिक स्थिति के दौरान विद्युत सर्किट की प्रतिक्रिया के रूप में जाना जाता हैtransient response।
क्षणिक प्रतिक्रिया 'टी' के बड़े मूल्यों के लिए शून्य होगी। आदर्श रूप से, 't' का यह मान अनंत होना चाहिए। लेकिन, व्यावहारिक रूप सेfive time constants पर्याप्त हैं
ग्राहकों की उपस्थिति या अनुपस्थिति
के कारण प्रतिक्रिया में ग्राहक आते हैं sudden changeविद्युत सर्किट और / या स्विचिंग कार्रवाई के कारण लागू होने वाले स्रोतों में। दो संभव स्विचिंग क्रियाएं हैं। वे स्विच खोल रहे हैं और स्विच बंद कर रहे हैं।
transient भाग जाएगा not presentएक विद्युत सर्किट या नेटवर्क की प्रतिक्रिया में, यदि इसमें केवल प्रतिरोध होते हैं। चूंकिresistor वोल्टेज और करंट की किसी भी राशि को समायोजित करने की क्षमता रखता है।
transient part occurs ऊर्जा भंडारण तत्वों की उपस्थिति के कारण विद्युत सर्किट या नेटवर्क की प्रतिक्रिया में inductor and capacitor। क्योंकि वे उन तत्वों में संग्रहीत ऊर्जा को तुरंत नहीं बदल सकते हैं।
प्रेरक व्यवहार
मान लें कि स्विचिंग क्रिया t = 0 पर होती है।Inductor currentजब स्विचिंग एक्शन होता है, तो तुरंत नहीं बदलता है। इसका मतलब है, स्विचिंग एक्शन के ठीक बाद प्रारंभ करनेवाला का मान स्विचिंग एक्शन से ठीक पहले जैसा होगा।
गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ $ i_L (0 ^ +) = i_L (0 ^ -) $ $
संधारित्र व्यवहार
capacitor voltageस्विचिंग एक्शन होने पर, इंस्ट्रक्टर करंट के समान तुरंत नहीं बदलता है। इसका मतलब है कि, स्विचिंग एक्शन के ठीक बाद कैपेसिटर वोल्टेज का मान स्विचिंग एक्शन से ठीक पहले जैसा होगा।
गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ $ v_c (0 ^ +) = v_c (0 ^ -) $ $
स्थिर राज्य प्रतिक्रिया
क्षणिक प्रतिक्रिया होने के बाद भी बनी रहने वाली समय प्रतिक्रिया का हिस्सा 'टी' के बड़े मूल्यों के लिए शून्य मान बन जाता है steady state response। इसका मतलब है, स्थिर स्थिति के दौरान प्रतिक्रिया में कोई क्षणिक हिस्सा नहीं होगा।
प्रेरक व्यवहार
यदि स्वतंत्र स्रोत लंबे समय तक एक या एक से अधिक प्रेरक और प्रतिरोधक (वैकल्पिक) वाले इलेक्ट्रिक सर्किट या नेटवर्क से जुड़ा है, तो उस विद्युत सर्किट या नेटवर्क को स्थिर स्थिति में कहा जाता है। इसलिए, उस विद्युत परिपथ के प्रारंभकर्ता (ओं) में संग्रहित ऊर्जा अधिकतम और स्थिर होती है।
गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ अधिकतम और स्थिर
$ \ Rightarrow i_L = $ अधिकतम और स्थिर
इसलिए, प्रारंभ करनेवाला एक के रूप में कार्य करता है constant current source स्थिर अवस्था में।
प्रारंभ करनेवाला में वोल्टेज होगा
$ $ V_L = L \ frac {di_ {L}} {dt} = 0V $$
तो, प्रारंभ करनेवाला एक के रूप में कार्य करता है short circuit स्थिर अवस्था में।
संधारित्र व्यवहार
यदि स्वतंत्र स्रोत एक लंबे समय के लिए एक या अधिक कैपेसिटर और प्रतिरोधक (वैकल्पिक) वाले इलेक्ट्रिक सर्किट या नेटवर्क से जुड़ा है, तो उस विद्युत सर्किट या नेटवर्क को स्थिर स्थिति में कहा जाता है। इसलिए, उस विद्युत परिपथ के संधारित्र (एस) में संग्रहित ऊर्जा अधिकतम और स्थिर होती है।
गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ अधिकतम और स्थिर
$ \ Rightarrow v_c = $ अधिकतम और स्थिर
इसलिए, संधारित्र एक के रूप में कार्य करता है constant voltage source स्थिर अवस्था में।
संधारित्र के माध्यम से बहने वाला वर्तमान होगा
$ $ i_c = C \ frac {DV_c} {dt} = 0A $$
तो, संधारित्र एक के रूप में कार्य करता है open circuit स्थिर अवस्था में।
श्रृंखला आरएल सर्किट की प्रतिक्रिया खोजना
निम्नलिखित को धयान मे रखते हुए series RL circuit आरेख।
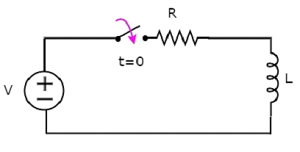
उपरोक्त सर्किट में, switch रखा गया था opent = 0 तक और इसे t = 0. पर बंद कर दिया गया था, इसलिए V वोल्ट्स वाले DC वोल्टेज स्रोत श्रृंखला RL सर्किट से इस तत्काल तक जुड़ा नहीं है। इसलिए, वहाँ हैno initial current प्रारंभ करनेवाला के माध्यम से बहती है।
सर्किट आरेख, जब switch में है closed स्थिति निम्न आकृति में दिखाई गई है।
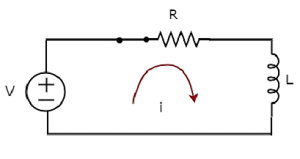
अब, वर्तमान i डीसी वोल्टेज स्रोत होने के बाद से पूरे सर्किट में प्रवाहित होता है V वोल्ट श्रृंखला आरएल सर्किट से जुड़ा हुआ है।
अब, आवेदन करें KVL पाश के आसपास।
$ $ V = Ri + L \ frac {di} {dt} $ $
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
उपरोक्त समीकरण एक प्रथम क्रम विभेदक समीकरण है और यह के रूप में है
$ \ frac {डाई} {dt} + Py = Q $Equation 2
द्वारा comparing समीकरण 1 और समीकरण 2, हमें निम्नलिखित संबंध मिलेंगे।
$ $ x = t $ $
$ $ य = मैं $ $
$ $ P = \ frac {R} {L} $ $
$ $ Q = \ frac {V} {L} $ $
solution समीकरण 2 होगा
$ तु ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
कहाँ पे, k निरंतर है।
स्थान, समीकरण 3 में x, y, P & Q के मान।
$ यानी ^ {\ int {lgroup \ frac {R} {L} \ rgroup} dt} = = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ _ lgroup / frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow यानी ^ {\ lgroup \ frac {R} {L} \ rgroup t} = = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} / Agroup t} dt + कश्मीर $
$ \ Rightarrow अर्थात ^ {\ lgroup \ frac {R} {L} \ rgroup t} = = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ "frac [{}} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
हम जानते हैं कि सर्किट में कोई प्रारंभिक प्रवाह नहीं है। इसलिए, स्थानापन्न, t = 0 और = 0 स्थिरांक का मान ज्ञात करने के लिए समीकरण 4 में k।
$ $ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $ $
$ $ 0 = \ frac {V} {R} + k (1) $ $
$ $ k = - \ frac {V} {R} $ $
स्थान, समीकरण 4 में k का मान।
$ $ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
$ $ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
इसलिए current सर्किट के माध्यम से बह रहा है
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
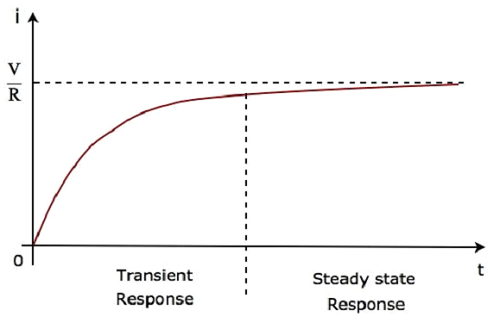
इसलिए, श्रृंखला आरएल सर्किट की प्रतिक्रिया, जब यह डीसी वोल्टेज स्रोत द्वारा उत्साहित होती है, तो निम्नलिखित दो शब्द होते हैं।
पहला शब्द $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ के साथ मेल खाता है transient response।
दूसरा शब्द $ \ frac {V} {R} $ के साथ मेल खाता है steady state response। इन दो प्रतिक्रियाओं को निम्न आकृति में दिखाया गया है।
हम समीकरण 5 को इस प्रकार फिर से लिख सकते हैं -
$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
कहाँ पे, τ है time constant और इसका मूल्य $ \ frac {L} {R} $ के बराबर है।
समीकरण 5 और समीकरण 6 दोनों समान हैं। लेकिन, हम कुछ मानों को प्रतिस्थापित करके समीकरण 6 से सर्किट के माध्यम से बहने वाली वर्तमान तरंग के उपरोक्त तरंग को आसानी से समझ सकते हैंt जैसे 0, τ, 2τ, 5τ, आदि।
सर्किट के माध्यम से बहने वाली वर्तमान तरंग के उपरोक्त तरंग में, क्षणिक प्रतिक्रिया शून्य से पांच समय स्थिरांक पेश करेगी, जबकि स्थिर राज्य प्रतिक्रिया पांच समय स्थिरांक से प्रस्तुत करेगी।