नेटवर्क सिद्धांत - निष्क्रिय तत्व
इस अध्याय में, हम रेजिस्टर, इंडक्टर और कैपेसिटर जैसे निष्क्रिय तत्वों के बारे में विस्तार से चर्चा करेंगे। हमें प्रतिरोधों के साथ शुरू करते हैं।
अवरोध
रेसिस्टर की मुख्य कार्यक्षमता या तो विरोध करती है या विद्युत प्रवाह के प्रवाह को प्रतिबंधित करती है। इसलिए, वर्तमान प्रवाह और / या विभाजन (साझा) वोल्टेज की मात्रा को सीमित करने के लिए प्रतिरोधों का उपयोग किया जाता है।
प्रतिरोधक के माध्यम से बहने वाली धारा I एम्पीयर है और इसके पार वोल्टेज V वोल्ट है। symbol वर्तमान, I और वोल्टेज के साथ रोकनेवाला, V को निम्न आकृति में दिखाया गया है।
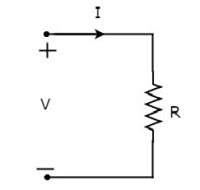
इसके अनुसार Ohm’s lawप्रतिरोधक के पार वोल्टेज, इसके माध्यम से बहने वाली विद्युत धारा और उस प्रतिरोधक का प्रतिरोध है। Mathematically, यह के रूप में प्रतिनिधित्व किया जा सकता है
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
कहाँ पे, R एक प्रतिरोधक का प्रतिरोध है।
समीकरण 2 से, हम यह निष्कर्ष निकाल सकते हैं कि प्रतिरोधक के माध्यम से प्रवाहित धारा प्रतिरोधक के पार लागू वोल्टेज के सीधे आनुपातिक होती है और प्रतिरोधक के प्रतिरोध के व्युत्क्रमानुपाती होती है।
Power एक विद्युत सर्किट तत्व के रूप में प्रतिनिधित्व किया जा सकता है
$ P = VI $Equation 3
स्थान, समीकरण ३ समीकरण ३ में।
$ पी = (आईआर) मैं $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
स्थानापन्न, समीकरण २ समीकरण ३ में।
$ P = V \ lgroup \ frac {V} {R} \ rgroup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
इसलिए, हम समीकरण 3 से 5 में उल्लिखित सूत्रों में से किसी एक का उपयोग करके रोकनेवाला में विस्थापित शक्ति की मात्रा की गणना कर सकते हैं।
प्रारंभ करनेवाला
सामान्य तौर पर, इंडिकेटर्स में कई मोड़ होंगे। इसलिए, वे चुंबकीय प्रवाह का उत्पादन करते हैं जब इसके माध्यम से प्रवाह होता है। इसलिए, एक प्रारंभ करनेवाला द्वारा उत्पादित कुल चुंबकीय प्रवाह की मात्रा वर्तमान पर निर्भर करती है, मैं इसके माध्यम से बहता हूं और उनके पास रैखिक संबंध हैं।
Mathematically, यह लिखा जा सकता है
$ $ \ Psi \: \ Alpha \: मैं $ $
$$ \ Rightarrow \ Psi = LI $$
कहाँ पे,
Ψ कुल चुंबकीय प्रवाह है
L एक प्रारंभ करनेवाला की प्रेरण है
प्रारंभ करनेवाला के माध्यम से बहने वाला I I एम्पीयर है और इसके पार वोल्टेज V वोल्ट है। symbolवर्तमान I और वोल्टेज V के साथ प्रारंभ करनेवाला निम्न आकृति में दिखाए गए हैं।
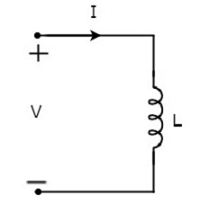
इसके अनुसार Faraday’s law, प्रारंभ में वोल्टेज को इस प्रकार लिखा जा सकता है
$ $ V = \ frac {d \ psi} {dt} $ $
उपर्युक्त समीकरण में स्थानापन्न Ψ = LI ।
$ $ V = \ frac {d (LI)} {dt} $ $
$$ \ Rightarrow V = L \ frac {dI} {dt} $ $
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $ $
उपरोक्त समीकरणों से, हम यह निष्कर्ष निकाल सकते हैं कि वहाँ मौजूद है linear relationship वोल्टेज से प्रारंभ करनेवाला और इसके माध्यम से बहने वाले वर्तमान के बीच।
हम जानते हैं कि power एक विद्युत सर्किट तत्व के रूप में प्रतिनिधित्व किया जा सकता है
$ $ पी = VI $ $
उपरोक्त समीकरण में $ V = L \ frac {dI} {dt} $ सब्स्टीट्यूट।
$ $ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $ $
उपरोक्त समीकरण को एकीकृत करके, हम प्राप्त करेंगे energy एक प्रारंभ करनेवाला के रूप में संग्रहीत
$ $ W = \ frac {1} {2} LI ^ 2 $ $
तो, प्रारंभ करनेवाला ऊर्जा को चुंबकीय क्षेत्र के रूप में संग्रहीत करता है।
संधारित्र
सामान्य तौर पर, एक संधारित्र में दो चालन प्लेट होते हैं, जो एक ढांकता हुआ माध्यम से अलग होते हैं। यदि संधारित्र में सकारात्मक वोल्टेज लागू किया जाता है, तो यह सकारात्मक चार्ज को संग्रहीत करता है। इसी प्रकार, यदि संधारित्र के पार ऋणात्मक वोल्टेज लगाया जाता है, तो यह ऋणात्मक आवेश को संग्रहीत करता है।
तो, संधारित्र में संग्रहीत चार्ज की मात्रा लागू वोल्टेज पर निर्भर करती है Vइसके पार और उनके बीच रैखिक संबंध हैं। गणितीय रूप से, इसे लिखा जा सकता है
$ $ Q \: \ Alpha \: V $$
$$ \ Rightarrow Q = CV $ $
कहाँ पे,
Q संधारित्र में संग्रहित आवेश होता है।
C संधारित्र का समाई है।
संधारित्र के माध्यम से बहने वाला वर्तमान I एम्पीयर है और इसके पार वोल्टेज V वोल्ट है। वर्तमान I और वोल्टेज V के साथ संधारित्र का प्रतीक निम्नलिखित आकृति में दिखाया गया है।
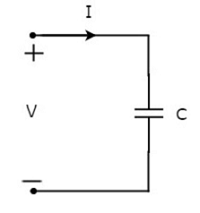
हम जानते हैं कि current इसके अलावा कुछ नहीं है time rate of flow of charge। गणितीय रूप से, इसका प्रतिनिधित्व किया जा सकता है
$ $ I = \ frac {dQ} {dt} $ $
उपरोक्त समीकरण में $ Q = CV $ को प्रतिस्थापित करें।
$ $ I = \ frac {d (CV)} {dt} $ $
$$ \ Rightarrow I = C \ frac {dV} {dt} $ $
$$ \ Rightarrow V = \ frac {1} {C} \ int मैं $ $ d
उपरोक्त समीकरणों से, हम यह निष्कर्ष निकाल सकते हैं कि वहाँ मौजूद है linear relationship संधारित्र के बीच वोल्टेज और इसके माध्यम से प्रवाहित धारा के बीच।
हम जानते हैं कि power एक विद्युत सर्किट तत्व के रूप में प्रतिनिधित्व किया जा सकता है
$ $ पी = VI $ $
उपर्युक्त समीकरण में $ I = C \ frac {dV} {dt} $।
$ $ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $ $
उपरोक्त समीकरण को एकीकृत करके, हम प्राप्त करेंगे energy के रूप में संधारित्र में संग्रहीत
$ $ W = \ frac {1} {2} CV ^ 2 $ $
तो, संधारित्र ऊर्जा को विद्युत क्षेत्र के रूप में संग्रहीत करता है।