नेटवर्क सिद्धांत - समतुल्य सर्किट
यदि एक सर्किट में दो या अधिक समान निष्क्रिय तत्व होते हैं और विशेष रूप से श्रृंखला प्रकार या समानांतर प्रकार से जुड़े होते हैं, तो हम उन्हें एक समान निष्क्रिय तत्व से बदल सकते हैं। इसलिए, इस सर्किट को एक कहा जाता हैequivalent circuit।
इस अध्याय में, हम निम्नलिखित दो समतुल्य सर्किटों के बारे में चर्चा करते हैं।
- श्रृंखला बराबर सर्किट
- समानांतर समतुल्य सर्किट
श्रृंखला बराबर सर्किट
यदि समान निष्क्रिय तत्व जुड़े हुए हैं series, फिर वही करंट इन सभी तत्वों से होकर बहेगा। लेकिन, वोल्टेज प्रत्येक तत्व में विभाजित हो जाता है।
निम्नलिखित को धयान मे रखते हुए circuit diagram।
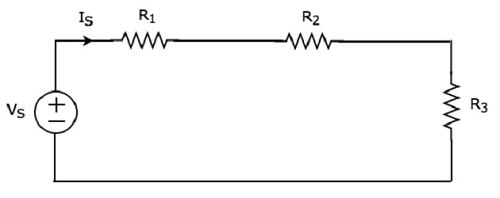
इसमें एक वोल्टेज स्रोत (वी एस ) और तीन प्रतिरोधों में आर 1 , आर 2 और आर 3 के प्रतिरोध हैं । ये सभी तत्व श्रृंखला में जुड़े हुए हैं। इन सभी तत्वों के माध्यम से वर्तमान आईएस बहता है।
उपरोक्त सर्किट में केवल एक जाल है। KVL equation इस जाल के आसपास है
$ $ V_S = V_1 + V_2 + V_3 $$
उपर्युक्त समीकरण में $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ और $ V_3 = I_S R_3 $।
$ $ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$
उपरोक्त समीकरण $ V_S = I_S R_ {Eq} $ के रूप में है, जहां
$ $ R_ {Eq} = R_1 + R_2 + R_3 $$
equivalent circuit diagram दिए गए सर्किट को निम्न आकृति में दिखाया गया है।
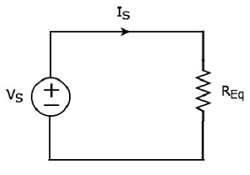
इसका मतलब है, यदि कई प्रतिरोधों को श्रृंखला में जोड़ा जाता है, तो हम उन्हें एक के साथ बदल सकते हैं equivalent resistor। इस समतुल्य प्रतिरोधक का प्रतिरोध उन सभी कई प्रतिरोधों के प्रतिरोधों के योग के बराबर होता है।
Note 1- यदि 'N' में L 1 , L 2 , ..., L N के इंडक्शन वाले इंडिकेटर्स श्रृंखला में जुड़े हैं, तो एequivalent inductance होगा
$$ L_ {Eq} = L_1 + L_2 + ... + L_N $ $
Note 2- यदि 'N' कैपेसिटर में C 1 , C 2 , ..., C N की कैपेसिटेंस हैं, तो श्रृंखला में जुड़े हुए हैं, तो एequivalent capacitance होगा
$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $ $
समानांतर समतुल्य सर्किट
यदि समान निष्क्रिय तत्व जुड़े हुए हैं parallel, फिर एक ही वोल्टेज प्रत्येक तत्व में बनाए रखा जाएगा। लेकिन, प्रत्येक तत्व के माध्यम से प्रवाहित धारा विभाजित हो जाती है।
निम्नलिखित को धयान मे रखते हुए circuit diagram।

इसका एक ही वर्तमान स्रोत (I S ) और तीन प्रतिरोधक हैं जिनमें R 1 , R 2 और R 3 के प्रतिरोध हैं । ये सभी तत्व समानांतर में जुड़े हुए हैं। इन सभी तत्वों में वोल्टेज (V S ) उपलब्ध है।
ग्राउंड नोड को छोड़कर उपरोक्त सर्किट में केवल एक प्रमुख नोड (पी) है। KCL equation इस मूल नोड (P) पर है
$ $ I_S = I_1 + I_2 + I_3 $ $
उपर्युक्त समीकरण में $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ और $ I_3 = \ frac {V_S} {R_3} $।
$ $ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $ $
$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $ $
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} [{_3} \ rgroup} \ right] $$
उपरोक्त समीकरण V S = I S R E Eq के रूप में है,
$ $ R_ {Eq} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup: $$
$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $ $
equivalent circuit diagram दिए गए सर्किट को निम्न आकृति में दिखाया गया है।
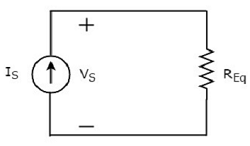
इसका मतलब है, यदि कई प्रतिरोधों को समानांतर में जोड़ा जाता है, तो हम उन्हें एक समान प्रतिरोधक के साथ बदल सकते हैं। इसका प्रतिरोध कियाequivalent resistor उन सभी प्रतिरोधों के प्रत्येक प्रतिरोध के पारस्परिक योग के योग के बराबर है।
Note 1- यदि 'N' में L 1 , L 2 , ..., L N के इंडक्शन वाले इंडिकेटर्स समानांतर में जुड़े हैं, तो aequivalent inductance होगा
$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $ $
Note 2- यदि 'N' कैपेसिटर में C 1 , C 2 , ..., C N की कैपेसिटेंस हैं, तो समानांतर में जुड़े हुए हैं, तो aequivalent capacitance होगा
$ $ C_ {Eq} = C_1 + C_2 + ... + C_N $ $