ऊंचाई और दूरी - हल उदाहरण

क्यू 1 - एक टॉवर के पैर से 375 मीटर की दूरी पर, टॉवर का शीर्ष 45 ° की ऊंचाई के कोण पर मनाया जाता है, फिर टॉवर की ऊंचाई (मीटर में) है?

A - 375

बी - 450

सी - 225

डी - 250

Answer - A

Explanation

From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

Q 2 - किसी बिंदु से किसी मीनार की ऊँचाई का कोण 90 मीटर है जो कि खाट ^-1 (4/5) है। तब मीनार की ऊँचाई कितनी होती है

A - 45

बी - 90

सी - 112.5

डी - 150

Answer - C

Explanation

Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

क्यू 3 - स्तर की जमीन पर, एक टॉवर के शीर्ष के कोण का कोण 30 ° है। 20 मीटर के करीब बढ़ते हुए, ऊंचाई का कोण 45 ° है। टॉवर की ऊंचाई।

A - 10

बी - √3

सी - 10√3

डी - 20√3

Answer - C

Explanation

Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

क्यू 4 - दो ऊर्ध्वाधर टावरों के शीर्ष की ऊंचाई के कोणों को टावरों के पैर से जुड़ने वाली रेखाओं के मध्य बिंदु से देखा जाता है 45 ° और 60 °। टावरों की ऊंचाई का अनुपात।

ए - :3: 2

बी - :3: 1

सी - 2: √3

डी - 2: 1

Answer - B

Explanation

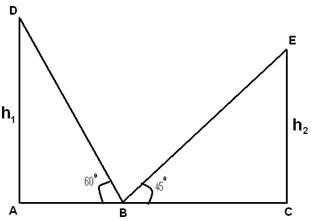
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

क्यू 5 - दो टावरों की ऊंचाई 90 मीटर और 45 मीटर है। उनके शीर्ष से जुड़ने वाली रेखा क्षैतिज के साथ एक कोण 450 बनाती है फिर दो टावरों के बीच की दूरी होती है

A - 22.5 मी

बी - 45 मीटर

सी - 60 मीटर

डी - 30 मीटर

Answer - B

Explanation

Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

क्यू 6 - एक स्तर पी पर एक बिंदु पी से, शीर्ष टॉवर के उत्थान का कोण 60 ° है। यदि टॉवर 180 मीटर ऊंचा है, तो टॉवर के पैर से बिंदु P की दूरी है

A - 60√3

बी - 40√3

सी - 30√3

डी - 20√3

Answer - A

Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

क्यू 7 - 25 मीटर ऊंचे टॉवर का शीर्ष बिजली के खंभे के निचले भाग के साथ 450 की ऊंचाई और कोण के शीर्ष के साथ 30 डिग्री की ऊंचाई के कोण बनाता है। विद्युत पोल की ऊंचाई ज्ञात कीजिए।

A - 25√3

बी - २५ ((√3-1) / √3)

सी - 25 / √3

डी - 25 ((1-)3) / 13)

Answer - B

Explanation

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

क्यू 8 - एक पर्यवेक्षक 1.4 मीटर लंबा एक टॉवर से 10 away3 दूर है। टावर के शीर्ष पर उसकी आंख से ऊंचाई का कोण 60 ° है। मीनार की ऊँचाई है

ए - 12.4 मीटर

बी - 6.2 मीटर

सी - 11.4√3 मीटर

डी - 11.4 मीटर

Answer - D

Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

क्यू 9 - एक आदमी टॉवर से सबसे ऊपर एक नाव को देख रहा है जो टावर से दूर है। जब नाव टॉवर से 75 मीटर की दूरी पर होती है, तो नाव 60 ° के अवसाद का कोण बनाती है। 10 सेकंड के बाद अवसाद का कोण 45 ° हो जाता है। नाव की अनुमानित गति क्या है, यह मानते हुए कि यह अभी भी पानी में चल रहा है?

A - 54 किमी प्रति घंटे

बी - 64 किमी प्रति घंटे

सी - 24 किमी प्रति घंटे

डी - 19.8 किमी प्रति घंटे

Answer - D

Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

क्यू 10 - दो टावरों के बीच क्षैतिज दूरी 90 मीटर है। पहले शीर्ष के कोणीय अवसाद को दूसरे के शीर्ष से देखा जाता है जो 180 मीटर ऊंचा है। 450 पहले की ऊंचाई है

ए - 90 m3 मीटर

बी - 45 मीटर

सी - 90 मीटर

डी - 150 मीटर

Answer - C

Explanation