Region of Convergence (ROC)
Variasi kisaran σ yang konvergen transformasi Laplace disebut daerah konvergensi.
Properti ROC Transformasi Laplace
ROC berisi garis-garis strip yang sejajar dengan sumbu jω pada bidang s.

Jika x (t) benar-benar integral dan berdurasi terbatas, maka ROC adalah seluruh bidang-s.
Jika x (t) adalah sekuens sisi kanan maka ROC: Re {s}> σ o .
Jika x (t) adalah deret sisi kiri maka ROC: Re {s} <σ o .
Jika x (t) adalah urutan dua sisi maka ROC adalah kombinasi dari dua daerah.
ROC dapat dijelaskan dengan menggunakan contoh-contoh yang diberikan di bawah ini:
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$L.T[x(t)] = L.T[e-^{at}u(t)] = {1 \over S+a}$
$ Re{} \gt -a $
$ ROC:Re{s} \gt >-a$

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ L.T[x(t)] = L.T[e^{at}u(t)] = {1 \over S-a} $
$ Re{s} < a $
$ ROC: Re{s} < a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$L.T[x(t)] = L.T[e^{-at}u(t)+e^{at}u(-t)] = {1 \over S+a} + {1 \over S-a}$
Untuk ${1 \over S+a} Re\{s\} \gt -a $
Untuk ${1 \over S-a} Re\{s\} \lt a $

Mengacu pada diagram di atas, daerah kombinasi terletak dari –a sampai a. Karenanya,
$ ROC: -a < Re{s} < a $
Kausalitas dan Stabilitas
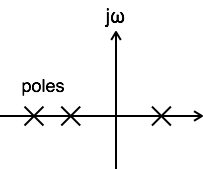
Agar sistem menjadi kausal, semua kutub fungsi transfernya harus separuh kanan bidang-s.

Suatu sistem dikatakan stabil ketika semua kutub dari fungsi transfernya terletak pada separuh kiri bidang-s.

Suatu sistem dikatakan tidak stabil ketika setidaknya satu kutub dari fungsi transfernya bergeser ke bagian kanan bidang-s.
Suatu sistem dikatakan stabil secara marginal bila setidaknya satu kutub dari fungsi transfernya terletak pada sumbu jω bidang s.

ROC dari Fungsi Dasar
| f (t) | F (s) | ROC |
|---|---|---|
| $u(t)$ | $${1\over s}$$ | KOP: Re {s}> 0 |
| $ t\, u(t) $ | $${1\over s^2} $$ | KOP: Re {s}> 0 |
| $ t^n\, u(t) $ | $$ {n! \over s^{n+1}} $$ | KOP: Re {s}> 0 |
| $ e^{at}\, u(t) $ | $$ {1\over s-a} $$ | ROC: Re {s}> a |
| $ e^{-at}\, u(t) $ | $$ {1\over s+a} $$ | ROC: Re {s}> -a |
| $ e^{at}\, u(t) $ | $$ - {1\over s-a} $$ | ROC: Re {s} <a |
| $ e^{-at}\, u(-t) $ | $$ - {1\over s+a} $$ | ROC: Re {s} <-a |
| $ t\, e^{at}\, u(t) $ | $$ {1 \over (s-a)^2} $$ | ROC: Re {s}> a |
| $ t^{n} e^{at}\, u(t) $ | $$ {n! \over (s-a)^{n+1}} $$ | ROC: Re {s}> a |
| $ t\, e^{-at}\, u(t) $ | $$ {1 \over (s+a)^2} $$ | ROC: Re {s}> -a |
| $ t^n\, e^{-at}\, u(t) $ | $${n! \over (s+a)^{n+1}} $$ | ROC: Re {s}> -a |
| $ t\, e^{at}\, u(-t) $ | $$ - {1 \over (s-a)^2} $$ | ROC: Re {s} <a |
| $ t^n\, e^{at}\, u(-t) $ | $$ - {n! \over (s-a)^{n+1}} $$ | ROC: Re {s} <a |
| $ t\, e^{-at}\,u(-t) $ | $$ - {1 \over (s+a)^2} $$ | ROC: Re {s} <-a |
| $ t^n\, e^{-at}\, u(-t) $ | $$ - {n! \over (s+a)^{n+1}} $$ | ROC: Re {s} <-a |
| $ e^{-at} \cos \, bt $ | $$ {s+a \over (s+a)^2 + b^2 } $$ | |
| $ e^{-at} \sin\, bt $ | $$ {b \over (s+a)^2 + b^2 } $$ |