Properti Z-Transforms
Z-Transform memiliki properti berikut:
Properti Linearitas
Jika $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
dan $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Kemudian properti linieritas menyatakan itu
$a\, x (n) + b\, y (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} a\, X(Z) + b\, Y(Z)$
Properti Pergeseran Waktu
Jika $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Kemudian properti Time shifting menyatakan itu
$x (n-m) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} z^{-m} X(Z)$
Perkalian dengan Properti Urutan Eksponensial
Jika $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Kemudian perkalian dengan properti urutan eksponensial menyatakan bahwa
$a^n\, . x(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z/a)$
Properti Pembalikan Waktu
Jika $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Kemudian properti pembalikan waktu menyatakan itu
$x (-n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(1/Z)$
Diferensiasi dalam Z-Domain ATAU Perkalian dengan n Properti
Jika $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Kemudian perkalian dengan n atau diferensiasi pada properti domain-z menyatakan bahwa
$ n^k x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} [-1]^k z^k{d^k X(Z) \over dZ^K} $
Properti Konvolusi
Jika $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
dan $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Kemudian properti konvolusi menyatakan itu
$x(n) * y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z)$
Properti Korelasi
Jika $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
dan $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Kemudian properti korelasi menyatakan itu
$x(n) \otimes y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z^{-1})$
Nilai Awal dan Nilai Akhir Teorema
Teorema nilai awal dan nilai akhir transformasi-z ditentukan untuk sinyal kausal.
Teorema Nilai Awal
Untuk sinyal kausal x (n), teorema nilai awal menyatakan bahwa
$ x (0) = \lim_{z \to \infty }X(z) $
Ini digunakan untuk mencari nilai awal sinyal tanpa melakukan invers z-transform
Teorema Nilai Akhir
Untuk sinyal kausal x (n), teorema nilai akhir menyatakan bahwa
$ x ( \infty ) = \lim_{z \to 1} [z-1] X(z) $
Ini digunakan untuk mencari nilai akhir dari sinyal tanpa melakukan invers z-transform.
Region of Convergence (ROC) dari Z-Transform
Kisaran variasi z yang konvergensi transformasi-z disebut wilayah konvergensi transformasi-z.
Properti ROC dari Z-Transforms
ROC transformasi-z ditandai dengan lingkaran pada bidang-z.
ROC tidak mengandung kutub apapun.
Jika x (n) adalah urutan sebab akibat durasi terbatas atau urutan sisi kanan, maka ROC adalah seluruh bidang-z kecuali pada z = 0.
Jika x (n) adalah urutan anti-sebab akibat berdurasi terbatas atau urutan sisi kiri, maka ROC adalah seluruh bidang-z kecuali pada z = ∞.
Jika x (n) adalah urutan sebab akibat durasi tak terhingga, ROC berada di luar lingkaran dengan jari-jari aie | z | > a.
Jika x (n) adalah urutan anti-sebab akibat berdurasi tak terhingga, ROC adalah interior lingkaran dengan jari-jari aie | z | <a.
Jika x (n) adalah durasi terbatas urutan dua sisi, maka ROC adalah seluruh bidang-z kecuali pada z = 0 & z = ∞.
Konsep ROC dapat dijelaskan dengan contoh berikut:
Example 1: Temukan z-transform dan ROC dari $a^n u[n] + a^{-}nu[-n-1]$
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z \over Z-a} + {Z \over Z {-1 \over a}}$
$$ ROC: |z| \gt a \quad\quad ROC: |z| \lt {1 \over a} $$
Plot ROC memiliki dua kondisi sebagai a> 1 dan a <1, karena Anda tidak mengetahui a.

Dalam hal ini, tidak ada kombinasi ROC.
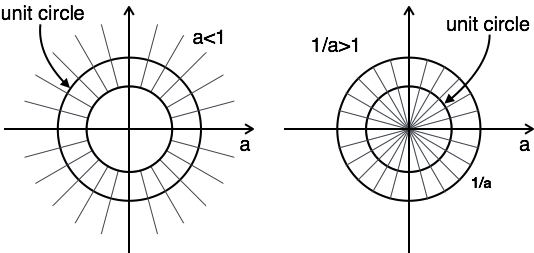
Di sini, kombinasi ROC berasal $a \lt |z| \lt {1 \over a}$
Karenanya untuk masalah ini, transformasi-z dimungkinkan jika a <1.
Kausalitas dan Stabilitas
Kondisi kausalitas untuk sistem LTI waktu diskrit adalah sebagai berikut:
Sistem LTI waktu diskrit adalah kausal kapan
KOP berada di luar kutub terluar.
Dalam Fungsi transfer H [Z], urutan pembilang tidak boleh lebih kecil dari urutan penyebut.
Kondisi Stabilitas untuk Sistem LTI Waktu Diskrit
Sistem LTI waktu diskrit stabil saat
fungsi sistemnya H [Z] termasuk lingkaran satuan | z | = 1.
semua kutub dari fungsi transfer terletak di dalam lingkaran satuan | z | = 1.
Z-Transformasi Sinyal Dasar
| x (t) | X [Z] |
|---|---|
| $\delta$ | 1 |
| $u(n)$ | ${Z\over Z-1}$ |
| $u(-n-1)$ | $ -{Z\over Z-1}$ |
| $\delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z \over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z \over Z-a}$ |
| $n\,a^n u[n]$ | ${aZ \over |Z-a|^2}$ |
| $n\,a^n u[-n-1] $ | $- {aZ \over |Z-a|^2}$ |
| $a^n \cos \omega n u[n] $ | ${Z^2-aZ \cos \omega \over Z^2-2aZ \cos \omega +a^2}$ |
| $a^n \sin \omega n u[n] $ | $ {aZ \sin \omega \over Z^2 -2aZ \cos \omega +a^2 } $ |