Teknik Sampling Sinyal
Ada tiga jenis teknik pengambilan sampel:
Pengambilan sampel impuls.
Pengambilan sampel alami.
Pengambilan sampel Flat Top.
Pengambilan Sampel Impuls
Pengambilan sampel impuls dapat dilakukan dengan mengalikan sinyal input x (t) dengan rangkaian impuls $ \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $ periode 'T'. Di sini, amplitudo impuls berubah sehubungan dengan amplitudo sinyal input x (t). Output dari sampler diberikan oleh
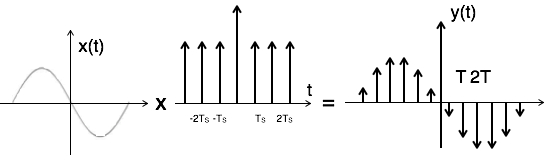
$ y (t) = x (t) × $ kereta impuls
$ = x (t) × \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $
$ y (t) = y _ {\ delta} (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} x (nt) \ delta (t-nT) \, ... \, ... 1 $
Untuk mendapatkan spektrum sinyal sampel, pertimbangkan Transformasi Fourier persamaan 1 di kedua sisi
$ Y (\ omega) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s) $
Ini disebut pengambilan sampel ideal atau pengambilan sampel impuls. Anda tidak dapat menggunakan ini secara praktis karena lebar pulsa tidak boleh nol dan pembangkitan rangkaian impuls secara praktis tidak dimungkinkan.
Pengambilan Sampel Alami
Pengambilan sampel natural mirip dengan pengambilan sampel impuls, kecuali rangkaian impuls diganti dengan rangkaian pulsa periode T. yaitu Anda mengalikan sinyal input x (t) ke rangkaian pulsa $ \ Sigma_ {n = - \ infty} ^ {\ infty} P ( t-nT) $ seperti yang ditunjukkan di bawah ini

Output dari sampler adalah
$ y (t) = x (t) \ times \ text {pulsa kereta} $
$ = x (t) \ kali p (t) $
$ = x (t) \ times \ Sigma_ {n = - \ infty} ^ {\ infty} P (t-nT) \, ... \, ... (1) $
Representasi deret Fourier eksponensial dari p (t) dapat diberikan sebagai
$ p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {jn \ omega_s t} \, ... \, ... (2) $
$ = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {j 2 \ pi nf_s t} $
Di mana $ F_n = {1 \ over T} \ int _ {- T \ over 2} ^ {T \ over 2} p (t) e ^ {- jn \ omega_s t} dt $
$ = {1 \ di atas TP} (n \ omega_s) $
Gantikan nilai F n dalam persamaan 2
$ \ oleh karena itu p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} {1 \ over T} P (n \ omega_s) e ^ {jn \ omega_s t} $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) e ^ {jn \ omega_s t} $
Gantikan p (t) dalam persamaan 1
$ y (t) = x (t) \ kali p (t) $
$ = x (t) \ times {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, e ^ {jn \ omega_s t} $
$ y (t) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ {jn \ omega_s t} $
Untuk mendapatkan spektrum sinyal sampel, pertimbangkan transformasi Fourier di kedua sisi.
$ FT \, [y (t)] = FT [{1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ { jn \ omega_s t}] $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, FT \, [x (t) \, e ^ {jn \ omega_s t}] $
Menurut properti pergeseran frekuensi
$ FT \, [x (t) \, e ^ {jn \ omega_s t}] = X [\ omega-n \ omega_s] $
$ \ oleh karena itu \, Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, X [\ omega-n \ omega_s] $
Pengambilan Sampel Flat Top
Selama transmisi, noise diperkenalkan di bagian atas pulsa transmisi yang dapat dengan mudah dihilangkan jika pulsa dalam bentuk flat top. Di sini, bagian atas sampel datar yaitu amplitudo konstan. Oleh karena itu, ini disebut sebagai sampling atas rata atau sampling praktis. Pengambilan sampel flat top menggunakan rangkaian sampel dan tahan.

Secara teoritis, sinyal sampel dapat diperoleh dengan konvolusi pulsa persegi panjang p (t) dengan sinyal sampel ideal katakanlah y δ (t) seperti yang ditunjukkan pada diagram:
yaitu $ y (t) = p (t) \ times y_ \ delta (t) \, ... \, ... (1) $

Untuk mendapatkan spektrum sampel, pertimbangkan transformasi Fourier di kedua sisi untuk persamaan 1
$ Y [\ omega] = KAKI \, [P (t) \ kali y_ \ delta (t)] $
Dengan pengetahuan tentang properti konvolusi,
$ Y [\ omega] = P (\ omega) \, Y_ \ delta (\ omega) $
Di sini $ P (\ omega) = T Sa ({\ omega T \ over 2}) = 2 \ sin \ omega T / \ omega $
Tingkat Nyquist
Ini adalah laju pengambilan sampel minimum di mana sinyal dapat diubah menjadi sampel dan dapat dipulihkan kembali tanpa distorsi.
Laju nyquist f N = 2f m hz
Interval Nyquist = $ {1 \ over fN} $ = $ {1 \ over 2fm} $ detik.
Sampling Sinyal Band Pass
Dalam hal sinyal band pass, spektrum sinyal band pass X [ω] = 0 untuk frekuensi di luar rentang f 1 ≤ f ≤ f 2 . Frekuensi f 1 selalu lebih besar dari nol. Plus, tidak ada efek aliasing jika f s > 2f 2 . Tetapi itu memiliki dua kelemahan:
Tingkat pengambilan sampel sebanding dengan f 2 . Ini memiliki batasan praktis.
Spektrum sinyal sampel memiliki celah spektral.
Untuk mengatasi hal ini, teorema band pass menyatakan bahwa sinyal input x (t) dapat diubah menjadi sampelnya dan dapat dipulihkan kembali tanpa distorsi saat frekuensi sampling f s <2f 2 .
Juga,
$$ f_s = {1 \ over T} = {2f_2 \ over m} $$
Di mana m adalah bilangan bulat terbesar <$ {f_2 \ over B} $
dan B adalah bandwidth sinyal. Jika f 2 = KB, maka
$$ f_s = {1 \ over T} = {2KB \ over m} $$
Untuk sinyal band pass bandwidth 2f m dan laju sampling minimum f s = 2 B = 4f m ,
spektrum sinyal sampel diberikan oleh $ Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} \, X [\ omega - 2nB] $