Ragionamento - Sillogismo
Il significato del sillogismo dato dai greci è Deduction. È una specie di argomentazione logica.
Definizione di alcuni termini importanti
Ci sono alcuni termini indicati di seguito che hanno un ruolo importante nella risoluzione dei problemi sul sillogismo.
Proposition- la proposizione è una frase che fa dichiarazioni. La proposizione consiste di 3 parti che sono a) soggetto, b) predicato ec) la relazione tra soggetto e predicato. Di seguito vengono fornite alcune proposizioni.
- Tutte le coste sono spiagge.
- Nessuno studente è onesto.
- Alcuni documenti sono segreti.
Subject and Predicate- Il soggetto è quella parte di cui si dice qualcosa. D'altra parte, il predicato è la parte correlata al soggetto. Ad esempio, dalle proposizioni precedenti le coste, gli studenti, i documenti sono soggetti mentre le spiagge, l'onesto e il segreto sono predicati.
Tipi di proposizioni categoriali
Universal Proposition- La proposizione universale è quella che include completamente il soggetto o lo esclude completamente. Ad esempio: nessuno studente è intelligente. La proposizione universale è ulteriormente classificata come segue:
Universal positive proposition - Quando il modulo è all X are Yallora si chiama proposizione positiva. È generalmente indicato con una letteraA.
Universal negative proposition - Quando il modulo è no X are T, allora si chiama proposizione negativa. È indicato daE.
Particular proposition- È la proposizione che mostra il soggetto parzialmente o lo esclude in parte ma non completamente. Ad esempio, alcuni gatti sono di cotone. È anche suddiviso nelle seguenti tipologie:
Particular positive proposition - Forme come some X are Usono chiamate proposizioni positive particolari. Sono codificati comeI.
Particular negative proposition - Forme come Some T are not P per esempio, some cats are not coils è chiamata proposizione negativa particolare e codificata come O.
Mediate inference- Qui la conclusione è tratta da due affermazioni. Esempio: "tutte le labbra sono bobine" e "tutte le palle sono mazze". Quindi la conclusione sarà "tutte le labbra sono spire".
Immediate inference- Qui la conclusione sarà presa da una sola proposizione. Ad esempio, se l'affermazione è "tutti gli insegnanti sono dio", la conclusione sarà "alcuni insegnanti sono dio".
Due importanti metodi di inferenza immediata
Questi metodi includono conversione, contrapposizione ecc.
Implications- Supponiamo che, dato che "tutti i gatti sono spiagge", sia vero che la conclusione "alcuni gatti sono spiagge". Quindi, se una data proposizione è di categoria A, allora mostra anche che la conclusione di tipo I deve essere vera.
Conversion - Consiste di 2 passaggi.
Step 1 - Il soggetto verrà convertito in predicato e viceversa.
Step 2 - La proposta che viene data verrà modificata di conseguenza.
For Example −
Statements- Tutti i gatti sono rastrelliere. Tutte le borse sono scaffali. Alcune borse sono borse.
Conclusions -
1. Alcuni gatti sono borse.
2. Alcuni rack sono gatti.
3. Alcuni rack sono borse.
A - Solo 1
B - Solo 2 e 3
C - Solo 1 e 2
D - Solo 1 e 3
Solution −
Risposta - Opzione B
Il modo pittorico di rappresentare le proposizioni è formulato da Eulero. Ci sono quattro modi in cui la relazione potrebbe essere stabilita secondo quattro proposizioni.
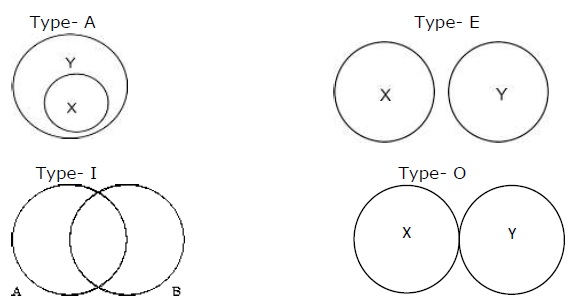
Tipo - A sta per "All X are Y", Type - E sta per "No X are Y", Type - I sta per "Some A are B" e Type - O sta per "Some X are not Y".
For Example −
Statements −Alcune fotocamere sono laptop.
Alcuni laptop sono telefoni.
Alcuni telefoni sono tablet.
Conclusions −
I - Almeno alcuni tablet sono fotocamere
II - Esiste la possibilità che tutti i tablet siano laptop
III - Nessuno dei tablet è un laptop
Solution −
Diagramma del cerchio -
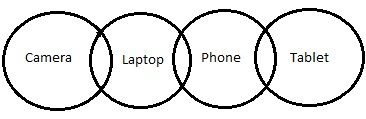
Secondo il diagramma sopra,
Segue la conclusione III. Ma la parola "possibilità" è stata menzionata nella dichiarazione. Quindi controlliamo le possibilità.
Il nuovo diagramma sarà:
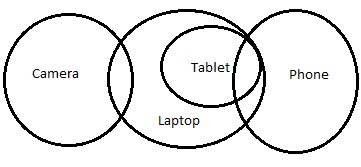
Ma in questo caso, la conclusione III non segue. Segue la conclusione II o la conclusione III.