適切な分数の乗算のモデリング

前書き

面積モデルを使用して分数を乗算してみましょう。面積モデルは、2つの分数を乗算したときに何が起こるかをよく示しています。問題は2次元で見られます。高さを1つの分数で表し、幅を別の分数で表します。この種のつながりを数学で見ることが重要です。

問題1：

面積モデル$ \ frac {1} {3} $ × $ \ frac {1} {3} $を使用して分数を乗算します

解決

Step 1:

この問題では、$ \ frac {1} {3} $の$ \ frac {1} {3} $を見つけたいと思います

Step 2:

まず、長方形の高さを3つの等しい部分に分割します。

Step 3:

$ \ frac {1} {3} $を表すために1つの部分に陰影を付けます

Step 4:

次に、幅を3つの等しい部分に分割し、1つの部分をシェーディングして$ \ frac {1} {3} $にします。

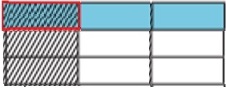
Step 5:

これで、製品を理解できます。陰影が重なる部分が分子を表します。部品の総数は分母を表します。合計9つのパーツがあり、パーツの1つがオーバーラップしています。

Step 6:

したがって、積は$ \ frac {1} {9} $です。

$ \ frac {1} {3} $ × $ \ frac {1} {3} $ = $ \ frac {1} {9} $

問題2：

面積モデル$ \ frac {2} {3} $ × $ \ frac {1} {3} $を使用して分数を乗算します

解決

Step 1:

この問題では、$ \ frac {1} {3} $の$ \ frac {2} {3} $を見つけたいと思います

Step 2:

まず、長方形の高さを3つの等しい部分に分割します。

Step 3:

$ \ frac {1} {3} $を表すために1つの部分に陰影を付けます

Step 4:

次に、幅を3つの等しい部分に分割し、2つの部分をシェーディングして、$ \ frac {2} {3} $にします。

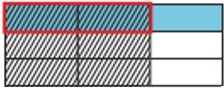
Step 5:

これで、製品を理解できます。陰影が重なる部分が分子を表します。部品の総数は分母を表します。合計9つのパーツがあり、2つのパーツがオーバーラップしています。

Step 6:

したがって、積は$ \ frac {2} {9} $です。

$ \ frac {2} {3} $ × $ \ frac {1} {3} $ = $ \ frac {2} {9} $

問題3：

面積モデルを使用して分数を乗算します$ \ frac {1} {2} $ × $ \ frac {1} {3} $

解決

Step 1:

この問題では、$ \ frac {1} {3} $の$ \ frac {1} {2} $を見つけたいと思います。

Step 2:

まず、長方形の高さを3つの等しい部分に分割します。

Step 3:

$ \ frac {1} {3} $を表すために1つの部分に陰影を付けます

Step 4:

次に、幅を2つの等しい部分に分割し、1つの部分に陰影を付けて$ \ frac {1} {2} $にします。

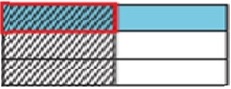
Step 5:

これで、製品を理解できます。陰影が重なる部分が分子を表します。部品の総数は分母を表します。合計6つのパーツがあり、パーツの1つがオーバーラップしています。

Step 6:

したがって、積は$ \ frac {1} {6} $です。

$ \ frac {1} {2} $ × $ \ frac {1} {3} $ = $ \ frac {1} {6} $