컨볼 루션 정리
마지막 튜토리얼에서 주파수 영역의 이미지에 대해 논의했습니다. 이 튜토리얼에서는 주파수 영역과 이미지 (공간 영역) 간의 관계를 정의합니다.
예를 들면
이 예를 고려하십시오.

주파수 영역에서 동일한 이미지를 다음과 같이 표현할 수 있습니다.

이제 이미지 또는 공간 영역과 주파수 영역 간의 관계는 무엇입니까? 이 관계는 Convolution 정리라고하는 정리로 설명 할 수 있습니다.
컨볼 루션 정리
공간 영역과 주파수 영역 간의 관계는 컨볼 루션 정리에 의해 설정 될 수 있습니다.
컨볼 루션 정리는 다음과 같이 나타낼 수 있습니다.
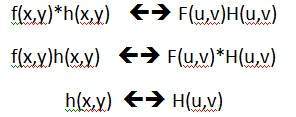
공간 영역의 컨볼 루션은 주파수 영역의 필터링과 같고 그 반대의 경우도 마찬가지입니다.
주파수 도메인의 필터링은 다음과 같이 나타낼 수 있습니다.

The steps in filtering are given below.
첫 번째 단계에서는 공간 영역에서 이미지를 사전 처리해야합니다. 이는 대비 또는 밝기를 증가시키는 것을 의미합니다.
그런 다음 이미지의 이산 푸리에 변환을 수행합니다.
그런 다음 이산 푸리에 변환을 중앙에 배치합니다. 이산 푸리에 변환을 모서리에서 중앙으로 가져옵니다.
그런 다음 필터링을 적용합니다. 즉, 푸리에 변환에 필터 함수를 곱합니다.
그런 다음 다시 DFT를 중앙에서 모서리로 이동합니다.
마지막 단계는 역 이산 푸리에 변환을 수행하여 결과를 주파수 영역에서 공간 영역으로 되 돌리는 것입니다.
이 후 처리 단계는 이미지의 모양을 높이는 전처리와 마찬가지로 선택 사항입니다.
필터
주파수 영역의 필터 개념은 컨볼 루션의 마스크 개념과 동일합니다.
이미지를 주파수 영역으로 변환 한 후 필터링 과정에서 일부 필터를 적용하여 이미지에 대해 다른 종류의 처리를 수행합니다. 처리에는 이미지 흐림, 이미지 선명 화 등이 포함됩니다.
이러한 목적을위한 일반적인 필터 유형은 다음과 같습니다.
- 이상적인 고역 통과 필터
- 이상적인 저역 통과 필터
- 가우스 고역 통과 필터
- 가우스 저역 통과 필터
다음 자습서에서는 필터에 대해 자세히 설명합니다.