관점 변환
인간의 눈은 가까이있는 사물을 볼 때 멀리있는 사물에 비해 더 크게 보입니다. 이를 일반적인 방식으로 관점이라고합니다. 변형은 한 상태에서 다른 상태로 객체 등을 전송하는 것입니다.
따라서 전반적으로 원근 변환은 3D 세계를 2D 이미지로 변환하는 작업을 처리합니다. 인간의 시각이 작동하는 원리와 카메라가 작동하는 원리가 같습니다.
왜 이런 일이 발생하는지, 가까이있는 물체는 더 크게 보이지만 멀리있는 물체는 도달하면 더 크게 보이지만 작아 보입니다.
이 토론은 참조 프레임의 개념으로 시작합니다.
참조 프레임 :
기준 프레임은 기본적으로 우리가 무언가를 측정하는 것과 관련된 일련의 값입니다.
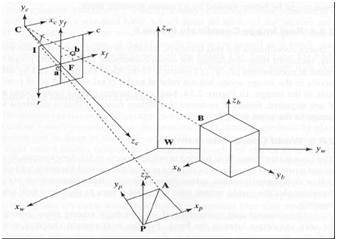
5 개의 기준 프레임
3 차원 세계 / 이미지 / 장면을 분석하기 위해서는 5 개의 서로 다른 참조 프레임이 필요합니다.
- Object
- World
- Camera
- Image
- Pixel
개체 좌표 프레임
객체 좌표 프레임은 객체 모델링에 사용됩니다. 예를 들어, 특정 개체가 다른 개체와 관련하여 적절한 위치에 있는지 확인합니다. 3D 좌표계입니다.
세계 좌표 프레임
세계 좌표 프레임은 3 차원 세계에서 객체를 상호 연관시키는 데 사용됩니다. 3D 좌표계입니다.
카메라 좌표 프레임
카메라 좌표 프레임은 카메라를 기준으로 개체를 연결하는 데 사용됩니다. 3D 좌표계입니다.
이미지 좌표 프레임
3D 좌표계가 아니라 2D 시스템입니다. 2D 이미지 평면에서 3D 점이 매핑되는 방식을 설명하는 데 사용됩니다.
픽셀 좌표 프레임
또한 2D 좌표계입니다. 각 픽셀에는 픽셀 좌표 값이 있습니다.
이 5 개의 프레임 사이의 변형

이것이 3D 장면이 픽셀 이미지와 함께 2D로 변환되는 방법입니다.
이제이 개념을 수학적으로 설명하겠습니다.
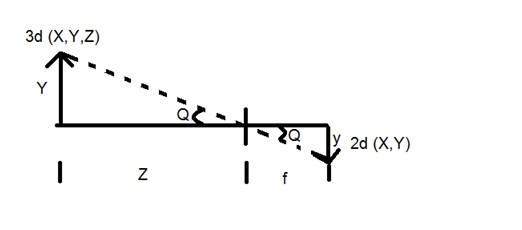
어디
Y = 3D 객체
y = 2d 이미지
f = 카메라의 초점 거리
Z = 물체와 카메라 사이의 거리
이제이 변환에는 Q로 표시되는 두 개의 다른 각도가 형성됩니다.
첫 번째 각도는
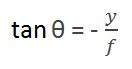
마이너스는 이미지가 반전되었음을 나타냅니다. 형성되는 두 번째 각도는 다음과 같습니다.

이 두 방정식을 비교하면

이 방정식에서 우리는 빛의 광선이 물체에서 부딪친 후 반사되어 카메라에서 통과하면 반전 이미지가 형성됨을 알 수 있습니다.
이 예를 통해이를 더 잘 이해할 수 있습니다.
예를 들면
형성된 이미지의 크기 계산
키가 5m이고 카메라에서 50m 떨어진 사람의 이미지를 촬영했다고 가정하고 초점 거리의 카메라를 사용하여 그 사람의 이미지 크기가 50mm라고 말해야합니다.
해결책:
초점 거리가 밀리미터이기 때문에 우리는 그것을 계산하기 위해 모든 것을 밀리미터 단위로 변환해야합니다.
그래서,
Y = 5000mm.
f = 50mm.
Z = 50000mm.
공식에 값을 입력하면
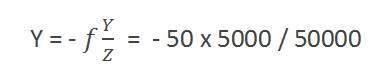
= -5mm.
다시 마이너스 기호는 이미지가 반전되었음을 나타냅니다.