DIP-퀵 가이드
소개
신호 처리는 아날로그 및 디지털 신호의 분석 및 처리를 다루고 신호에 대한 저장, 필터링 및 기타 작업을 다루는 전기 공학 및 수학 분야의 분야입니다. 이러한 신호에는 전송 신호, 사운드 또는 음성 신호, 이미지 신호 및 기타 신호 등이 포함됩니다.
이러한 모든 신호 중에서 입력이 이미지이고 출력도 이미지 인 신호 유형을 다루는 필드가 이미지 처리에서 수행됩니다. 이름에서 알 수 있듯이 이미지 처리를 다룹니다.
아날로그 이미지 처리와 디지털 이미지 처리로 더 나눌 수 있습니다.
아날로그 이미지 처리
아날로그 이미지 처리는 아날로그 신호에서 수행됩니다. 여기에는 2 차원 아날로그 신호 처리가 포함됩니다. 이 유형의 처리에서 이미지는 전기 신호를 변경하여 전기적 수단으로 조작됩니다. 일반적인 예는 텔레비전 이미지입니다.
디지털 이미지 처리는 광범위한 응용 분야로 인해 시간이 지남에 따라 아날로그 이미지 처리를 지배했습니다.
디지털 이미지 처리
디지털 이미지 처리는 디지털 이미지에 대한 작업을 수행하는 디지털 시스템 개발을 다룹니다.
이미지 란?
이미지는 2 차원 신호에 지나지 않습니다. 수학 함수 f (x, y)에 의해 정의됩니다. 여기서 x와 y는 수평 및 수직 두 좌표입니다.
임의의 지점에서 f (x, y) 값은 이미지의 해당 지점에서 픽셀 값을 제공합니다.

위의 그림은 현재 컴퓨터 화면에서보고있는 디지털 이미지의 예입니다. 그러나 실제로이 이미지는 0에서 255 사이의 숫자로 구성된 2 차원 배열 일뿐입니다.
| 128 | 30 | 123 |
| 232 | 123 | 321 |
| 123 | 77 | 89 |
| 80 | 255 | 255 |
각 숫자는 임의의 지점에서 함수 f (x, y)의 값을 나타냅니다. 이 경우 값 128, 230, 123은 각각 개별 픽셀 값을 나타냅니다. 그림의 차원은 실제로이 2 차원 배열의 차원입니다.
디지털 이미지와 신호의 관계
이미지가 2 차원 배열이면 신호와 어떤 관계가 있습니까? 이를 이해하려면 먼저 신호가 무엇인지 이해해야합니다.
신호
물리적 세계에서는 공간 또는 더 높은 차원에서 시간을 통해 측정 할 수있는 모든 양을 신호로 받아 들일 수 있습니다. 신호는 수학적 함수이며 일부 정보를 전달합니다. 신호는 1 차원 또는 2 차원 또는 더 높은 차원의 신호일 수 있습니다. 1 차원 신호는 시간이 지남에 따라 측정되는 신호입니다. 일반적인 예는 음성 신호입니다. 2 차원 신호는 다른 물리량에 대해 측정 된 신호입니다. 2 차원 신호의 예는 디지털 이미지입니다. 1 차원 또는 2 차원 신호와 더 높은 신호가 어떻게 형성되고 해석되는지에 대한 다음 튜토리얼에서 더 자세히 살펴볼 것입니다.
관계
두 관찰자 사이에서 정보를 전달하거나 물리적 세계에서 메시지를 방송하는 것은 신호이기 때문입니다. 여기에는 음성 또는 (인간의 음성) 또는 신호로서의 이미지가 포함됩니다. 우리가 말할 때부터 우리의 목소리는 음파 / 신호로 변환되고 우리가 말하는 사람과의 시간에 따라 변형됩니다. 뿐만 아니라 디지털 카메라의 작동 방식은 디지털 카메라에서 이미지를 수집하는 동안 시스템의 한 부분에서 다른 부분으로 신호를 전송하는 것과 관련이 있습니다.
디지털 이미지가 형성되는 방법
카메라에서 이미지를 캡처하는 것은 물리적 프로세스이기 때문입니다. 햇빛은 에너지 원으로 사용됩니다. 이미지 획득을 위해 센서 어레이가 사용됩니다. 따라서 햇빛이 물체에 떨어지면 해당 물체에서 반사 된 빛의 양이 센서에 의해 감지되고 감지 된 데이터의 양에 따라 연속 전압 신호가 생성됩니다. 디지털 이미지를 생성하려면이 데이터를 디지털 형식으로 변환해야합니다. 여기에는 샘플링 및 양자화가 포함됩니다. (나중에 논의됩니다). 샘플링 및 양자화의 결과로 디지털 이미지에 불과한 2 차원 배열 또는 숫자 행렬이 생성됩니다.
겹치는 필드
기계 / 컴퓨터 비전
머신 비전 또는 컴퓨터 비전은 입력이 이미지이고 출력이 일부 정보 인 시스템 개발을 다룹니다. 예 : 사람의 얼굴을 스캔하고 모든 종류의 자물쇠를 여는 시스템 개발. 이 시스템은 다음과 같습니다.

컴퓨터 그래픽
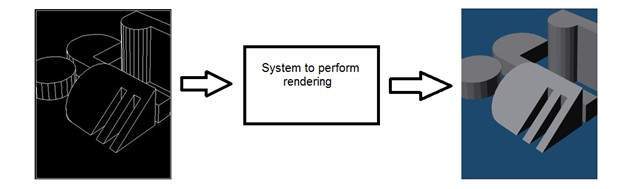
컴퓨터 그래픽은 일부 장치에서 이미지를 캡처하는 대신 개체 모델의 이미지 형성을 처리합니다. 예 : 개체 렌더링. 개체 모델에서 이미지 생성. 이러한 시스템은 다음과 같습니다.
인공 지능
인공 지능은 인간 지능을 기계에 넣는 연구입니다. 인공 지능은 이미지 처리에 많은 응용 분야를 가지고 있습니다. 예 : 의사가 X 선, MRI 등의 이미지를 해석하는 데 도움이되는 컴퓨터 보조 진단 시스템을 개발 한 다음 의사가 검사 할 눈에 띄는 부분을 강조 표시합니다.
신호 처리
신호 처리는 우산이며 이미지 처리는 그 밑에 있습니다. 물리적 세계 (3D 세계)에서 물체에 반사 된 빛의 양은 카메라의 렌즈를 통과하여 2D 신호가되어 이미지가 형성됩니다. 이 이미지는 신호 처리 방법을 사용하여 디지털화되고이 디지털 이미지는 디지털 이미지 처리에서 조작됩니다.
이 튜토리얼에서는 디지털 이미지 처리의 개념을 이해하는 데 필요한 신호 및 시스템의 기본 사항을 다룹니다. 세부 개념으로 이동하기 전에 먼저 간단한 용어를 정의하겠습니다.
신호
전기 공학에서 일부 정보를 나타내는 기본적인 양을 신호라고합니다. 정보가 무엇인지 즉, 아날로그 또는 디지털 정보는 중요하지 않습니다. 수학에서 신호는 일부 정보를 전달하는 기능입니다. 실제로 공간 또는 더 높은 차원에서 시간을 통해 측정 할 수있는 모든 양은 신호로 받아 들여질 수 있습니다. 신호는 모든 차원이 될 수 있으며 모든 형태가 될 수 있습니다.
아날로그 신호
신호는 시간과 관련하여 정의 된 아날로그 양일 수 있습니다. 연속적인 신호입니다. 이러한 신호는 연속 독립 변수를 통해 정의됩니다. 그들은 엄청난 수의 가치를 가지고 있기 때문에 분석하기가 어렵습니다. 값의 큰 샘플로 인해 매우 정확합니다. 이러한 신호를 저장하려면 실제 라인에서 무한 값을 얻을 수 있기 때문에 무한 메모리가 필요합니다. 아날로그 신호는 사인파로 표시됩니다.
예를 들면 :
인성
인간의 음성은 아날로그 신호의 예입니다. 당신이 말할 때 생성되는 음성은 압력 파의 형태로 공기를 통해 이동하므로 공간과 시간의 독립 변수와 기압에 해당하는 값을 갖는 수학 함수에 속합니다.
또 다른 예는 아래 그림에 표시된 sin wave입니다.
Y = sin (x) 여기서 x는 무의미합니다.

디지털 신호
아날로그 신호에 비해 디지털 신호는 분석하기가 매우 쉽습니다. 불연속 신호입니다. 그것들은 아날로그 신호의 전유입니다.
디지털이라는 단어는 이산 값을 나타내므로 특정 값을 사용하여 정보를 나타냅니다. 디지털 신호에서는 1과 0 (이진 값)을 나타내는 데 두 개의 값만 사용됩니다. 디지털 신호는 일정 기간 동안 취해진 아날로그 신호의 개별 샘플이기 때문에 아날로그 신호보다 정확도가 떨어집니다. 그러나 디지털 신호에는 노이즈가 없습니다. 그래서 그들은 오래 지속되고 해석하기 쉽습니다. 디지털 신호는 사각 파로 표시됩니다.
예를 들면 :
컴퓨터 키보드
키보드에서 키를 누를 때마다 해당 키의 ASCII 값을 포함하는 적절한 전기 신호가 키보드 컨트롤러로 전송됩니다. 예를 들어, 키보드 키 a를 눌렀을 때 생성되는 전기 신호는 문자 a의 ASCII 값인 0과 1의 형태로 97 자리 정보를 전달합니다.
아날로그와 디지털 신호의 차이점
| 비교 요소 | 아날로그 신호 | 디지털 신호 |
|---|---|---|
| 분석 | 어려운 | 분석 가능 |
| 대표 | 마디 없는 | 끊어진 |
| 정확성 | 더 정확한 | 덜 정확함 |
| 저장 | 무한한 기억 | 쉽게 저장 |
| 소음이 발생할 수 있음 | 예 | 아니 |
| 녹음 기법 | 원래 신호가 보존됩니다. | 신호 샘플을 수집하고 보존합니다. |
| 예 | 인간의 목소리, 온도계, 아날로그 전화 등 | 컴퓨터, 디지털 전화, 디지털 펜 등 |
시스템
시스템은 처리하는 입력 및 출력 유형에 의해 정의됩니다. 우리가 신호를 다루기 때문에 우리의 경우 우리 시스템은 수학적 모델, 코드 / 소프트웨어 또는 물리적 장치이거나 입력이 신호이고 해당 신호에 대해 처리를 수행하는 블랙 박스가 될 것입니다. 출력은 신호입니다. 입력을 여기라고하고 출력을 응답이라고합니다.

위 그림에서는 입력과 출력이 모두 신호이지만 입력이 아날로그 신호 인 시스템이 표시되었습니다. 그리고 출력은 디지털 신호입니다. 그것은 우리 시스템이 실제로 아날로그 신호를 디지털 신호로 변환하는 변환 시스템이라는 것을 의미합니다.
이 블랙 박스 시스템의 내부를 살펴 보겠습니다.
아날로그를 디지털 신호로 변환
이 아날로그에서 디지털로의 변환과 관련된 많은 개념이 있기 때문에 그 반대도 마찬가지입니다. 우리는 디지털 이미지 처리와 관련된 것에 대해서만 논의 할 것입니다. 커버에 관련된 두 가지 주요 개념이 있습니다.
Sampling
Quantization
견본 추출
이름에서 알 수 있듯이 샘플링은 샘플 채취로 정의 할 수 있습니다. x 축에서 디지털 신호 샘플을 가져옵니다. 샘플링은 독립 변수에서 수행됩니다. 이 수학 방정식의 경우 :
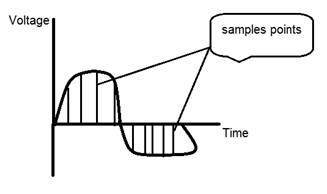
샘플링은 x 변수에서 수행됩니다. 또한 x 축 (무한 값)을 디지털로 변환하는 것은 샘플링에서 수행된다고 말할 수 있습니다.
샘플링은 업 샘플링과 다운 샘플링으로 더 나뉩니다. x 축의 값 범위가 작 으면 값 샘플을 늘립니다. 이를 업 샘플링이라고하고 그 반대의 경우는 다운 샘플링이라고합니다.
양자화
이름에서 알 수 있듯이 양자화는 양자 (파티션)로 나누는 것으로 정의 할 수 있습니다. 양자화는 종속 변수에서 수행됩니다. 샘플링과 반대입니다.
이 수학 방정식의 경우 y = sin (x)
양자화는 Y 변수에서 수행됩니다. Y 축에서 이루어집니다. y 축 무한 값을 1, 0, -1 (또는 다른 수준)으로 변환하는 것을 양자화라고합니다.
다음은 아날로그 신호를 디지털 신호로 변환하는 동안 관련된 두 가지 기본 단계입니다.
신호의 양자화는 아래 그림에 나와 있습니다.
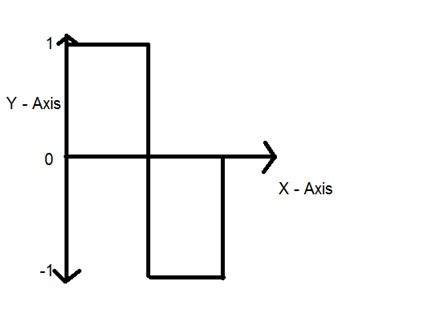
아날로그 신호를 디지털 신호로 변환해야하는 이유는 무엇입니까?
첫 번째 분명한 이유는 디지털 이미지 처리가 디지털 신호 인 디지털 이미지를 처리하기 때문입니다. 따라서 이미지가 캡처 될 때마다 디지털 형식으로 변환 된 다음 처리됩니다.
두 번째이자 중요한 이유는 디지털 컴퓨터로 아날로그 신호에 대한 작업을 수행하려면 해당 아날로그 신호를 컴퓨터에 저장해야한다는 것입니다. 그리고 아날로그 신호를 저장하기 위해서는이를 저장하기 위해 무한한 메모리가 필요합니다. 그리고 그것이 가능하지 않기 때문에 우리는 그 신호를 디지털 형식으로 변환 한 다음 디지털 컴퓨터에 저장 한 다음 작업을 수행합니다.
연속 시스템 vs 개별 시스템
연속 시스템
입력과 출력이 모두 연속 신호이거나 아날로그 신호 인 시스템 유형을 연속 시스템이라고합니다.
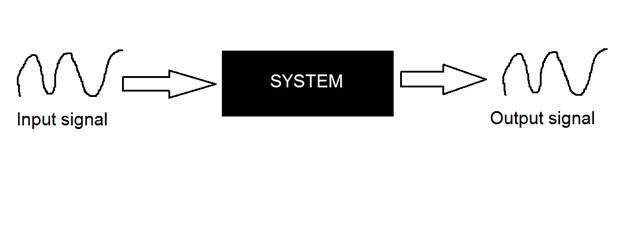
이산 시스템
입력과 출력이 모두 이산 신호이거나 디지털 신호 인 시스템 유형을 디지털 시스템이라고합니다.
카메라의 기원
카메라와 사진의 역사는 정확히 같지 않습니다. 카메라의 개념은 사진 개념 이전에 많이 소개되었습니다.
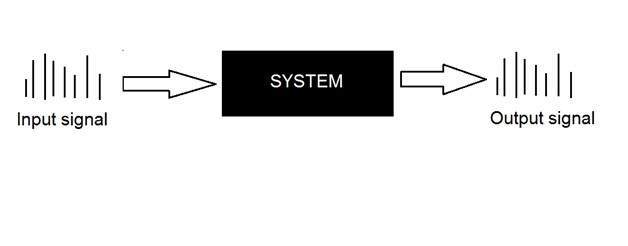
카메라 옵스큐라
카메라의 역사는 아시아에 있습니다. 카메라의 원리는 중국 철학자 MOZI에 의해 처음 소개되었습니다. 카메라 옵스큐라라고합니다. 카메라는이 원리에서 진화했습니다.
카메라 옵스큐라는 두 개의 다른 단어에서 진화했습니다. 카메라와 옵스큐라. 카메라라는 단어의 의미는 방 또는 일종의 금고이며 Obscura는 어둠을 의미합니다.
중국 철학자가 소개 한 개념은 벽에 주변의 이미지를 투영하는 장치로 구성됩니다. 그러나 그것은 중국인에 의해 지어지지 않았습니다.
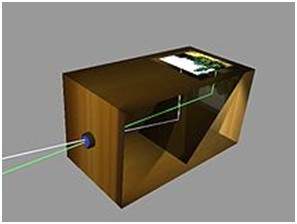
카메라 옵스큐라 생성
중국어의 개념은 일반적으로 Ibn al-Haitham으로 알려진 이슬람 과학자 Abu Ali Al-Hassan Ibn al-Haitham에 의해 현실화되었습니다. 그는 최초의 카메라 옵스큐라를 만들었습니다. 그의 카메라는 핀홀 카메라의 원리를 따릅니다. 그는이 장치를 약 1000 년에 만들었습니다.
휴대용 카메라
1685 년에 Johann Zahn이 최초의 휴대용 카메라를 제작했습니다. 이 장치가 출현하기 전에 카메라는 공간 크기로 구성되어 휴대용이 아니 었습니다. 아일랜드 과학자 로버트 보일과 로버트 훅이 만든 장치는 운반 가능한 카메라 였지만 여전히 그 장치는 한곳에서 다른 곳으로 옮기기에 매우 컸습니다.
사진의 기원
카메라 옵스 쿠라는 1000 년 무슬림 과학자에 의해 만들어졌습니다. 그러나 최초의 실제 사용은 영국 철학자 Roger Bacon이 13 세기에 설명했습니다. Roger는 일식 관찰을 위해 카메라 사용을 제안했습니다.
다 빈치
15 세기 이전에는 많은 개선이 있었지만 Leonardo di ser Piero da Vinci의 개선과 결과는 놀랍습니다. 다빈치는 위대한 예술가, 음악가, 해부학자, 전쟁의 시작가였습니다. 그는 많은 발명품으로 유명합니다. 그의 가장 유명한 그림 중 하나는 모나리자의 그림입니다.

다빈치는 핀홀 카메라의 원리에 따라 카메라 옵스큐라를 만들었을뿐만 아니라 그의 작품을위한 드로잉 보조 도구로도 사용합니다. Codex Atlanticus에 기술 된 그의 작업에서 카메라 옵스큐라의 많은 원칙이 정의되었습니다.
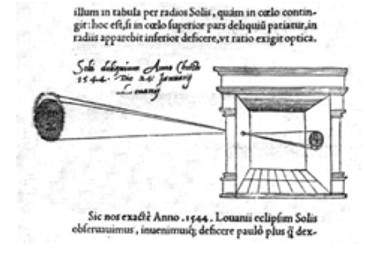
그의 카메라는 다음과 같이 설명 할 수있는 핀홀 카메라의 원리를 따릅니다.
조명 된 물체의 이미지가 작은 구멍을 통해 매우 어두운 방으로 침투하면 [반대쪽 벽에서] 이러한 물체를 적절한 형태와 색상으로 볼 수 있으며 광선의 교차로 인해 반대 위치에서 크기가 줄어 듭니다.
첫 번째 사진
첫 번째 사진은 1814 년 프랑스 발명가 Joseph Nicephore Niepce가 찍은 것입니다. 그는 백랍 판에 역청을 코팅 한 후 그 판을 빛에 노출시켜 르 그라의 창문에서 바라본 풍경의 첫 번째 사진을 찍습니다.

최초의 수중 사진
첫 번째 수중 사진은 영국 수학자 William Thomson이 방수 상자를 사용하여 촬영했습니다. 이것은 1856 년에 이루어졌습니다.

영화의 기원
영화의 기원은 미국 발명가이자 사진의 선구자로 여겨지는 조지 이스트만 (George Eastman)으로 알려진 자선가에 의해 소개되었습니다.
그는 영화 개발로 유명한 Eastman Kodak이라는 회사를 설립했습니다. 이 회사는 1885 년에 종이 필름 제조를 시작했습니다. 그는 처음에는 Kodak 카메라를 만든 다음 나중에 Brownie를 만들었습니다. 브라우니는 박스 카메라였으며 스냅 샷 기능으로 인기를 얻었습니다.

영화의 출현 이후, 카메라 산업은 다시 한번 붐을 일으켰고 하나의 발명이 다른 것으로 이어졌습니다.
라이카와 아르 거스
Leica와 argus는 각각 1925 년과 1939 년에 개발 된 두 개의 아날로그 카메라입니다. 카메라 라이카는 35mm 영화 필름을 사용하여 제작되었습니다.

Argus는 35mm 포맷을 사용하는 또 다른 카메라 아날로그 카메라였으며 라이카에 비해 다소 저렴했고 매우 인기가있었습니다.

아날로그 CCTV 카메라
1942 년 독일 엔지니어 Walter Bruch는 아날로그 CCTV 카메라의 최초 시스템을 개발하고 설치했습니다. 그는 1960 년에 컬러 TV를 발명 한 공로도 인정 받았습니다.
포토 팩
최초의 일회용 카메라는 1949 년 Photo Pac에 의해 소개되었습니다. 이 카메라는 필름 롤이 이미 포함 된 일회용 카메라였습니다. 이후 버전의 Photo pac은 방수 기능이 있으며 플래시도 있습니다.

디지털 카메라
Mavica by Sony
Mavica (마그네틱 비디오 카메라)는 1981 년 Sony가 출시 한 디지털 카메라 세계의 첫 번째 게임 체인저였습니다. 이미지는 플로피 디스크에 기록되었으며 나중에 모든 모니터 화면에서 볼 수 있습니다.
순수한 디지털 카메라가 아니라 아날로그 카메라였습니다. 그러나 플로피 디스크에 이미지를 저장하는 용량 때문에 인기를 얻었습니다. 이는 이제 이미지를 오래 지속될 수 있으며, 플로피에 많은 사진을 저장할 수 있으며 꽉 차면 새 공 디스크로 교체됩니다. Mavica는 디스크에 25 개의 이미지를 저장할 수 있습니다.
마비카가 소개 한 또 하나의 중요한 것은 0.3 메가 픽셀의 사진 캡처 용량이었습니다.

디지털 카메라
Fuji DS-1P camera 후지 필름 1988은 최초의 진정한 디지털 카메라였습니다.
Nikon D1 2.74 메가 픽셀 카메라이자 Nikon이 개발 한 최초의 상업용 디지털 SLR 카메라였으며 전문가들이 매우 저렴했습니다.

오늘날 디지털 카메라는 매우 높은 해상도와 품질로 휴대폰에 포함되어 있습니다.
디지털 이미지 처리는 매우 광범위한 응용 프로그램을 가지고 있으며 거의 모든 기술 분야가 DIP의 영향을 받기 때문에 DIP의 주요 응용 프로그램 중 일부만 논의하겠습니다.
디지털 이미지 처리는 카메라로 캡처 한 일상적인 이미지의 공간 해상도를 조정하는 데만 국한되지 않습니다. 사진의 밝기 등을 높이는 데 국한된 것이 아니라 그 이상입니다.
전자기파는 각 입자가 빛의 속도로 움직이는 입자의 흐름으로 생각할 수 있습니다. 각 입자에는 에너지 묶음이 포함되어 있습니다. 이 에너지 묶음을 광자라고합니다.
광자의 에너지에 따른 전자기 스펙트럼은 다음과 같습니다.

이 전자기 스펙트럼에서는 가시 스펙트럼 만 볼 수 있습니다. 가시 스펙트럼은 주로 일반적으로 (VIBGOYR)로 불리는 7 가지 색상을 포함합니다. VIBGOYR는 보라색, 남색, 파란색, 녹색, 주황색, 노란색 및 빨간색을 나타냅니다.
그러나 그것은 스펙트럼에서 다른 물질의 존재를 무효화하지 않습니다. 인간의 눈은 우리가 모든 물체를 본 보이는 부분 만 볼 수 있습니다. 그러나 카메라는 육안으로는 볼 수없는 다른 것들을 볼 수 있습니다. 예를 들어 : x 광선, 감마 광선 등 따라서 모든 분석도 디지털 이미지 처리에서 수행됩니다.
이 토론은 또 다른 질문으로 이어집니다.
왜 우리는 EM 스펙트럼의 다른 모든 것들을 분석해야합니까?
이 질문에 대한 답은 사실에 있습니다. XRay와 같은 다른 것들이 의료 분야에서 널리 사용 되었기 때문입니다. 감마선의 분석은 핵 의학 및 천문 관측에 널리 사용되기 때문에 필요합니다. EM 스펙트럼의 나머지 부분도 마찬가지입니다.
디지털 이미지 처리의 응용
디지털 이미지 처리가 널리 사용되는 주요 분야는 다음과 같습니다.
이미지 선명 화 및 복원
의료 분야
원격 감지
전송 및 인코딩
기계 / 로봇 비전
색상 처리
패턴 인식
비디오 처리
현미경 이미징
Others
이미지 선명 화 및 복원
여기에서 이미지 선명 화 및 복원은 최신 카메라에서 캡처 한 이미지를 처리하여 더 나은 이미지로 만들거나 원하는 결과를 얻기 위해 해당 이미지를 조작하는 것을 말합니다. Photoshop에서 일반적으로 수행하는 작업을 나타냅니다.
여기에는 확대 / 축소, 블러 링, 선명하게하기, 그레이 스케일에서 색상으로 변환, 가장자리 감지 및 그 반대로, 이미지 검색 및 이미지 인식이 포함됩니다. 일반적인 예는 다음과 같습니다.
원본 이미지

확대 된 이미지

흐릿한 이미지

선명한 이미지

가장자리

의료 분야
의료 분야에서 DIP의 일반적인 응용은 다음과 같습니다.
감마선 이미징
PET 스캔
X 레이 이미징
의료용 CT
UV 이미징
UV 이미징
원격 탐사 분야에서는 위성이나 매우 높은 지대에서 지구 영역을 스캔 한 후 분석하여 정보를 얻습니다. 원격 감지 분야에서 디지털 이미지 처리의 특정 응용 분야 중 하나는 지진으로 인한 인프라 손상을 감지하는 것입니다.
심각한 피해가 집중 되더라도 파악하는 데 시간이 오래 걸리기 때문입니다. 지진의 영향을받는 지역은 때때로 너무 넓기 때문에 사람의 눈으로 조사하여 피해를 추정 할 수 없습니다. 라고해도 매우 바쁘고 시간이 많이 걸리는 절차입니다. 이에 대한 해결책은 디지털 이미지 처리에서 찾을 수 있습니다. 영향을받은 지역의 이미지를 지상에서 캡처 한 다음 분석하여 지진으로 인한 다양한 유형의 피해를 감지합니다.
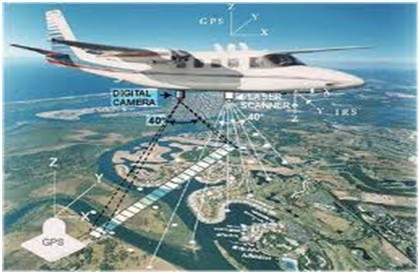
분석에 포함되는 주요 단계는 다음과 같습니다.
가장자리 추출
다양한 유형의 모서리 분석 및 향상
전송 및 인코딩
전선을 통해 전송 된 최초의 이미지는 해저 케이블을 통해 런던에서 뉴욕으로 전송되었습니다. 전송 된 사진은 아래와 같습니다.

전송 된 사진은 한 곳에서 다른 곳으로 도달하는 데 3 시간이 걸렸습니다.
이제 우리는 단 몇 초만에 한 대륙에서 다른 대륙으로 라이브 비디오 피드 또는 라이브 CCTV 영상을 볼 수 있다고 상상해보십시오. 이는이 분야에서도 많은 작업이 수행되었음을 의미합니다. 이 필드는 전송뿐만 아니라 인코딩에도 중점을 둡니다. 사진을 인코딩 한 다음 인터넷 등을 통해 스트리밍하기 위해 높거나 낮은 대역폭을 위해 다양한 형식이 개발되었습니다.
기계 / 로봇 비전
오늘날 로봇이 직면하고있는 많은 과제를 제외하고 여전히 가장 큰 과제 중 하나는 로봇의 비전을 높이는 것입니다. 로봇이 사물을보고, 식별하고, 장애물을 식별 할 수 있도록합니다.이 분야에서 많은 작업이 기여했으며 컴퓨터 비전의 완전한 다른 분야가 도입되었습니다.
장애물 감지
허들 감지는 이미지에서 다른 유형의 물체를 식별 한 다음 로봇과 허들 사이의 거리를 계산하여 이미지 처리를 통해 수행되는 일반적인 작업 중 하나입니다.

라인 추종자 로봇
오늘날 대부분의 로봇은 라인을 따라 작동하므로 라인 팔로워 로봇이라고합니다. 이것은 로봇이 경로를 따라 이동하고 일부 작업을 수행하는 데 도움이됩니다. 이것은 또한 이미지 처리를 통해 달성되었습니다.

색상 처리
색상 처리에는 사용되는 색상 이미지 및 다양한 색상 공간 처리가 포함됩니다. 예를 들어 RGB 색상 모델, YCbCr, HSV. 또한 이러한 컬러 이미지의 전송, 저장 및 인코딩을 연구합니다.
패턴 인식
패턴 인식에는 이미지 처리 및 기계 학습 (인공 지능의 한 분야)을 포함하는 다양한 다른 분야의 연구가 포함됩니다. 패턴 인식에서 이미지 처리는 이미지의 객체를 식별하는 데 사용되며 기계 학습은 패턴의 변화에 대해 시스템을 훈련시키는 데 사용됩니다. 패턴 인식은 컴퓨터 보조 진단, 필기 인식, 이미지 인식 등에 사용됩니다.
비디오 처리
비디오는 사진의 매우 빠른 움직임 일뿐입니다. 비디오 품질은 분당 프레임 / 사진 수와 사용중인 각 프레임의 품질에 따라 달라집니다. 비디오 처리에는 노이즈 감소, 디테일 향상, 모션 감지, 프레임 속도 변환, 종횡비 변환, 색 공간 변환 등이 포함됩니다.
차원의 개념을 이해하기 위해이 예를 살펴 보겠습니다.
달에 사는 친구가 있는데 그는 생일 선물로 선물을 보내려고합니다. 그는 당신의 지구상의 거주지에 대해 묻습니다. 유일한 문제는 달의 택배 서비스가 알파벳 주소를 이해하지 못하고 숫자 좌표 만 이해한다는 것입니다. 그럼 어떻게 그에게 지구상의 위치를 보내나요?
그것이 차원의 개념이 오는 곳입니다. 치수는 공간 내에서 특정 개체의 위치를 가리키는 데 필요한 최소 포인트 수를 정의합니다.
그러니 다시 지구상의 위치를 달의 친구에게 보내야하는 예로 돌아가 보겠습니다. 당신은 그에게 세 쌍의 좌표를 보냅니다. 첫 번째는 경도, 두 번째는 위도, 세 번째는 고도라고합니다.
이 세 좌표는 지구에서의 위치를 정의합니다. 처음 두 개는 사용자의 위치를 정의하고 세 번째는 해수면 위의 높이를 정의합니다.
즉, 지구상의 위치를 정의하는 데 3 개의 좌표 만 필요합니다. 그것은 당신이 3 차원적인 세상에 살고 있다는 것을 의미합니다. 따라서 이것은 차원에 대한 질문에 답할뿐만 아니라 우리가 3D 세계에 사는 이유에 대한 답이기도합니다.
디지털 이미지 처리와 관련하여이 개념을 연구하고 있으므로 이제이 차원 개념을 이미지와 연관 시키려고합니다.
이미지의 치수
따라서 우리가 3D 세계에 살고 있다면 3 차원 세계를 의미하고 캡처 한 이미지의 크기는 얼마입니까? 이미지는 2 차원이므로 이미지를 2 차원 신호로 정의하기도합니다. 이미지에는 높이와 너비 만 있습니다. 이미지에는 깊이가 없습니다. 아래 이미지를보세요.
위의 그림을 보면 높이와 너비 축인 두 개의 축만 있음을 알 수 있습니다. 이 이미지에서 깊이를 인식 할 수 없습니다. 이것이 이미지가 2 차원 신호라고 말하는 이유입니다. 그러나 우리의 눈은 3 차원 물체를 인식 할 수 있지만, 이것은 카메라가 어떻게 작동하고 이미지가 인식되는지에 대한 다음 튜토리얼에서 더 자세히 설명 될 것입니다.
이 토론은 3 차원 시스템이 2 차원에서 어떻게 형성되는지에 대한 몇 가지 다른 질문으로 이어집니다.
텔레비전은 어떻게 작동합니까?
위의 이미지를 보면 2 차원 이미지임을 알 수 있습니다. 3 차원으로 변환하려면 다른 차원이 필요합니다. 3 차원으로 시간을 가져 보겠습니다.이 경우 3 차원 시간에 걸쳐이 2 차원 이미지를 이동합니다. 텔레비전에서 발생하는 것과 동일한 개념으로 화면에있는 다른 물체의 깊이를 인식하는 데 도움이됩니다. 그것은 TV에 나오는 것이나 우리가 텔레비전 화면에서 보는 것이 3D라는 것을 의미합니까? 그럼 우리는 할 수 있습니다. 그 이유는 TV의 경우에는 동영상을 재생하기 때문입니다. 그러면 비디오는 다른 것이 아니라 2 차원 그림이 시간 차원에 따라 움직입니다. 2 차원 물체가 시간 인 3 차원 위로 움직이기 때문에 우리는 그것이 3 차원이라고 말할 수 있습니다.
신호의 다른 차원
1 차원 신호
1 차원 신호의 일반적인 예는 파형입니다. 수학적으로 다음과 같이 나타낼 수 있습니다.
F (x) = 파형
여기서 x는 독립 변수입니다. 1 차원 신호이므로 변수 x가 하나만 사용됩니다.
1 차원 신호의 그림 표현은 다음과 같습니다.
위 그림은 1 차원 신호를 보여줍니다.
이제 이것은 또 다른 질문으로 이어집니다. 즉, 1 차원 신호 임에도 불구하고 왜 두 개의 축이 있습니까? 이 질문에 대한 답은 그것이 1 차원 신호 임에도 불구하고 우리는 그것을 2 차원 공간에서 그리고 있다는 것입니다. 또는 우리가이 신호를 나타내는 공간이 2 차원이라고 말할 수 있습니다. 이것이 2 차원 신호처럼 보이는 이유입니다.
아래 그림을 보면 1 차원의 개념을 더 잘 이해할 수있을 것입니다.

이제 차원에 대한 초기 논의를 다시 참조하십시오. 위의 그림을 한 지점에서 다른 지점으로 양수로 된 실제 선을 고려하십시오. 이제이 선에있는 어떤 점의 위치를 설명해야한다면 하나의 숫자 만 필요합니다. 즉, 하나의 차원 만 의미합니다.
2 차원 신호
2 차원 신호의 일반적인 예는 이미 위에서 논의한 이미지입니다.

이미 살펴본 것처럼 이미지는 2 차원 신호입니다. 즉, 2 차원이 있습니다. 수학적으로 다음과 같이 나타낼 수 있습니다.
F (x, y) = 이미지
여기서 x와 y는 두 개의 변수입니다. 2 차원의 개념은 수학적으로 다음과 같이 설명 할 수도 있습니다.
이제 위 그림에서 사각형의 네 모서리에 각각 A, B, C 및 D로 레이블을 지정합니다. , 그림 AB의 한 선분과 다른 CD를 호출하면이 두 개의 평행선이 합쳐져 정사각형을 이루는 것을 볼 수 있습니다. 각 선분은 1 차원에 해당하므로이 두 선분은 2 차원에 해당합니다.
3 차원 신호
이름 그대로 3 차원 신호는 3 차원 신호를 의미합니다. 가장 일반적인 예는 처음에 우리 세계에서 논의되었습니다. 우리는 3 차원 세계에 살고 있습니다. 이 예제는 매우 정교하게 논의되었습니다. 3 차원 신호의 또 다른 예는 큐브 또는 체적 데이터이거나 가장 일반적인 예는 애니메이션 또는 3D 만화 캐릭터입니다.
3 차원 신호의 수학적 표현은 다음과 같습니다.
F (x, y, z) = 애니메이션 캐릭터.
또 다른 축 또는 차원 Z는 깊이의 환상을 제공하는 3 차원에 포함됩니다. 데카르트 좌표계에서는 다음과 같이 볼 수 있습니다.

4 차원 신호
4 차원 신호에는 4 차원이 포함됩니다. 처음 세 개는 (X, Y, Z)의 3 차원 신호와 동일하며, 여기에 추가되는 네 번째 신호는 T (시간)입니다. 시간은 종종 변화를 측정하는 방법 인 시간적 차원이라고합니다. 수학적으로 4 차원 신호는 다음과 같이 나타낼 수 있습니다.
F (x, y, z, t) = 애니메이션 영화.
4 차원 신호의 일반적인 예는 애니메이션 3D 영화 일 수 있습니다. 각각의 캐릭터가 3D 캐릭터이기 때문에 시간에 따라 움직이기 때문에 현실 세계와 같은 입체 영화의 환상을 보았습니다.
즉, 실제로 애니메이션 영화는 4 차원입니다. 즉, 4 차원 시간 동안 3D 캐릭터의 움직임입니다.
인간의 눈은 어떻게 작동합니까?
아날로그 및 디지털 카메라의 이미지 형성에 대해 논의하기 전에 먼저 인간의 눈에서 이미지 형성에 대해 논의해야합니다. 카메라가 따르는 기본 원리는 길에서 가져 왔기 때문에 인간의 눈은 작동합니다.
빛이 특정 물체에 떨어지면 물체를 비춘 후 다시 반사됩니다. 눈의 수정체를 통과 할 때 빛의 광선은 특정한 각도를 형성하고 벽의 뒷면 인 망막에 이미지가 형성됩니다. 형성된 이미지가 반전됩니다. 이 이미지는 뇌에 의해 해석되어 우리가 사물을 이해할 수있게합니다. 각도 형성으로 인해 우리는 우리가보고있는 물체의 높이와 깊이를인지 할 수 있습니다. 이것은 원근 변환 튜토리얼에서 더 자세히 설명되었습니다.
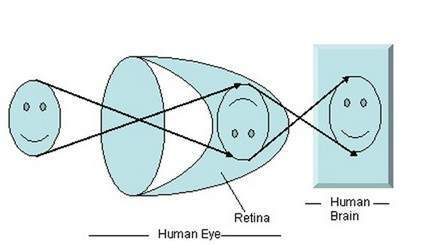
위의 그림에서 볼 수 있듯이 태양 광이 물체 (이 경우 물체가 얼굴)에 떨어지면 반사되어 렌즈를 통과 할 때 다른 광선이 다른 각도를 형성하고 물체가 뒷벽에 형성되었습니다. 그림의 마지막 부분은 대상이 뇌에 의해 해석되고 다시 반전되었음을 나타냅니다.
이제 아날로그 및 디지털 카메라의 이미지 형성에 대해 다시 논의하겠습니다.
아날로그 카메라에서 이미지 형성
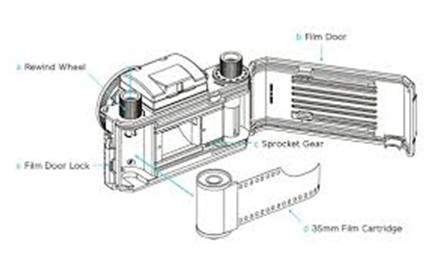
아날로그 카메라에서 이미지 형성은 이미지 형성에 사용되는 스트립에서 발생하는 화학 반응으로 인해 발생합니다.
아날로그 카메라에는 35mm 스트립이 사용됩니다. 그림에서 35mm 필름 카트리지로 표시됩니다. 이 스트립은 할로겐화은 (화학 물질)으로 코팅되어 있습니다.

아날로그 카메라에는 35mm 스트립이 사용됩니다. 그림에서 35mm 필름 카트리지로 표시됩니다. 이 스트립은 할로겐화은 (화학 물질)으로 코팅되어 있습니다.
빛은 광자 입자로 알려진 작은 입자 일 뿐이므로 이러한 광자 입자가 카메라를 통과하면 스트립의 할로겐화은 입자와 반응하여 이미지의 네거티브 인 은이됩니다.
더 잘 이해하려면이 방정식을 살펴보십시오.
광자 (가벼운 입자) + 할로겐화은? 은? 이미지 네거티브.

이미지 형성에는 내부의 빛 통과, 셔터 및 셔터 속도, 조리개 및 개방 개념과 관련된 다른 많은 개념이 포함되지만 지금은 다음 부분으로 넘어가겠습니다. 이러한 개념의 대부분은 셔터 및 조리개 튜토리얼에서 논의되었습니다.
이미지 형성에는 내부의 빛 통과, 셔터 및 셔터 속도, 조리개 및 개방 개념과 관련된 다른 많은 개념이 포함되지만 지금은 다음 부분으로 넘어가겠습니다. 이러한 개념의 대부분은 셔터 및 조리개 튜토리얼에서 논의되었습니다.
디지털 카메라의 이미지 형성
디지털 카메라에서 이미지 형성은 일어나는 화학 반응으로 인한 것이 아니라 이것보다 조금 더 복잡합니다. 디지털 카메라에서는 CCD 센서 어레이가 이미지 형성에 사용됩니다.
CCD 어레이를 통한 이미지 형성

CCD는 전하 결합 장치를 나타냅니다. 이미지 센서이며 다른 센서와 마찬가지로 값을 감지하여 전기 신호로 변환합니다. CCD의 경우 영상을 감지하여 전기 신호 등으로 변환
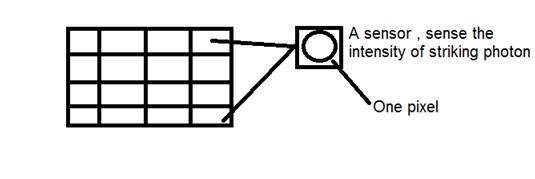
이 CCD는 실제로 배열 또는 직사각형 격자 모양입니다. 매트릭스의 각 셀이 광자의 강도를 감지하는 검열 관을 포함하는 매트릭스와 같습니다.
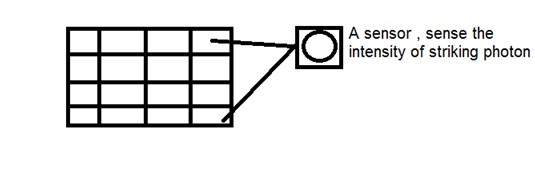
아날로그 카메라와 마찬가지로 디지털의 경우에도 빛이 물체에 떨어지면 빛이 물체에 닿은 후 반사되어 카메라 내부로 들어갑니다.
CCD 어레이 자체의 각 센서는 아날로그 센서입니다. 빛의 광자가 칩에 부딪히면 각 포토 센서에서 작은 전하로 유지됩니다. 각 센서의 반응은 센서 표면에 닿는 빛 또는 (광자) 에너지의 양과 직접적으로 같습니다.
이미 이미지를 2 차원 신호로 정의했고 CCD 어레이의 2 차원 형성으로 인해이 CCD 어레이에서 완전한 이미지를 얻을 수 있습니다.
제한된 수의 센서를 가지고 있으며 제한된 세부 사항을 캡처 할 수 있음을 의미합니다. 또한 각 센서는 그것에 부딪히는 각 광자 입자에 대해 하나의 값만 가질 수 있습니다.
따라서 충돌하는 광자의 수 (현재)가 계산되고 저장됩니다. 이를 정확하게 측정하기 위해 외부 CMOS 센서도 CCD 어레이와 함께 부착됩니다.
픽셀 소개
CCD 어레이의 각 센서 값은 개별 픽셀의 값을 각각 나타냅니다. 센서 수 = 픽셀 수. 이는 또한 각 센서가 하나의 값만 가질 수 있음을 의미합니다.
이미지 저장
CCD 어레이에 의해 저장된 전하는 한 번에 한 픽셀의 전압으로 변환됩니다. 추가 회로의 도움으로이 전압은 디지털 정보로 변환 된 다음 저장됩니다.
디지털 카메라를 제조하는 각 회사는 자체 CCD 센서를 만듭니다. 여기에는 Sony, Mistubishi, Nikon, Samsung, Toshiba, FujiFilm, Canon 등이 포함됩니다.
다른 요소 외에도 캡처 된 이미지의 품질은 사용 된 CCD 어레이의 유형과 품질에 따라 달라집니다.
이 튜토리얼에서는 조리개, 셔터, 셔터 속도, ISO와 같은 몇 가지 기본 카메라 개념에 대해 논의하고 좋은 이미지를 캡처하기위한 이러한 개념의 집합 적 사용에 대해 논의 할 것입니다.
구멍
조리개는 빛이 카메라 내부로 이동할 수있는 작은 구멍입니다. 여기 조리개 사진이 있습니다.

조리개 안에 물건과 같은 작은 칼날이 보일 것입니다. 이 블레이드는 닫혀서 열 수있는 팔각형 모양을 만듭니다. 따라서 더 많은 블레이드가 열릴수록 빛이 통과해야하는 구멍이 더 커질 것입니다. 구멍이 클수록 더 많은 빛이 들어갈 수 있습니다.
효과
조리개의 효과는 이미지의 밝기와 어두움과 직접적으로 일치합니다. 조리개 개구부가 넓 으면 더 많은 빛이 카메라로 통과 할 수 있습니다. 더 많은 빛은 더 많은 광자를 생성하여 궁극적으로 더 밝은 이미지를 만듭니다.
이에 대한 예가 아래에 나와 있습니다.
이 두 사진을 고려하십시오


오른쪽에있는 것이 더 밝아 보인다는 것은 카메라로 촬영했을 때 조리개가 활짝 열려 있음을 의미합니다. 왼쪽에있는 다른 사진과 비교하면 첫 번째 사진과 비교할 때 매우 어둡습니다.이 사진은 해당 이미지를 캡처했을 때 조리개가 크게 열리지 않았 음을 보여줍니다.
크기
이제 조리개 뒤에있는 수학에 대해 논의하겠습니다. 조리개의 크기는 f 값으로 표시됩니다. 그리고 이것은 조리개 개방에 반비례합니다.
다음은이 개념을 가장 잘 설명하는 두 가지 방정식입니다.
큰 조리개 크기 = 작은 f 값
작은 조리개 크기 = 더 큰 f 값
그림으로 다음과 같이 표현할 수 있습니다.
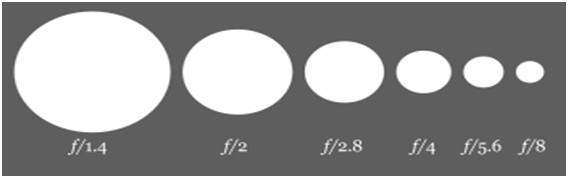
셔터
조리개 후 셔터가 나옵니다. 조리개를 통과 할 때 빛은 셔터로 직접 떨어집니다. 셔터는 실제로 덮개, 닫힌 창 또는 커튼으로 생각할 수 있습니다. 이미지가 형성되는 CCD 어레이 센서에 대해 이야기 할 때를 기억하십시오. 셔터 뒤에는 센서가 있습니다. 따라서 셔터는 조리개에서 통과 할 때 이미지 형성과 빛 사이에있는 유일한 것입니다.
셔터가 열리 자마자 빛이 이미지 센서에 떨어지고 이미지가 어레이에 형성됩니다.
효과
셔터를 사용하여 빛이 조금 더 오래 통과하면 이미지가 더 밝아집니다. 마찬가지로 셔터가 매우 빠르게 움직여서 통과 할 수있는 빛의 광자가 매우 적고 CCD 어레이 센서에 형성된 이미지가 매우 어두워지면 더 어두운 사진이 생성됩니다.
셔터에는 두 가지 주요 개념이 있습니다.
셔터 속도
셔터 시간
셔터 속도
셔터 속도는 셔터가 열리거나 닫히는 횟수라고 할 수 있습니다. 셔터가 얼마나 오래 열리거나 닫히는 지에 대해 말하는 것이 아닙니다.
셔터 시간
셔터 시간은 다음과 같이 정의 할 수 있습니다.
셔터가 열렸을 때 닫힐 때까지 걸리는 대기 시간을 셔터 시간이라고합니다.
이 경우 우리는 셔터가 몇 번 열리거나 닫혔는지에 대해 말하는 것이 아니라 얼마나 많은 시간이 활짝 열려 있는지에 대해 이야기하고 있습니다.
예를 들면 :
이런 식으로이 두 가지 개념을 더 잘 이해할 수 있습니다. 즉, 셔터가 15 번 열렸다가 닫히고 매번 1 초 동안 열렸다가 닫힙니다. 이 예에서 15는 셔터 속도이고 1 초는 셔터 시간입니다.
관계
셔터 속도와 셔터 시간 사이의 관계는 둘 다 서로 반비례한다는 것입니다.
이 관계는 아래 방정식에서 정의 할 수 있습니다.
더 빠른 셔터 속도 = 더 적은 셔터 시간
더 적은 셔터 속도 = 더 많은 셔터 시간.
설명:
필요한 시간이 적을수록 속도가 빨라집니다. 그리고 필요한 시간이 길수록 속도는 줄어 듭니다.
응용
이 두 개념은 함께 다양한 응용 프로그램을 만듭니다. 그들 중 일부는 아래에 나와 있습니다.
빠르게 움직이는 물체 :
빠르게 움직이는 물체의 이미지를 캡처하는 경우 자동차 등이 될 수 있습니다. 셔터 속도와 시간 조정은 많은 영향을 미칩니다.
따라서 이와 같은 이미지를 캡처하기 위해 두 가지 수정 사항을 적용합니다.
셔터 속도 높이기
셔터 시간 줄이기
일어나는 일은 우리가 셔터 속도를 높이면 셔터가 더 많이 열리거나 닫히는 것입니다. 이는 다른 빛의 샘플이 통과 할 수 있음을 의미합니다. 그리고 셔터 시간을 줄이면 즉시 장면을 캡처하고 셔터 게이트를 닫을 것입니다.
이렇게하면 빠르게 움직이는 물체의 선명한 이미지를 얻을 수 있습니다.
이해하기 위해이 예를 살펴 보겠습니다. 빠르게 움직이는 물이 떨어지는 이미지를 캡처한다고 가정합니다.
셔터 속도를 1 초로 설정하고 사진을 캡처합니다. 이것은 당신이 얻는 것입니다

그런 다음 셔터 속도를 더 빠른 속도로 설정하면 얻을 수 있습니다.

그런 다음 다시 셔터 속도를 더 빠르게 설정하면 얻을 수 있습니다.

마지막 사진에서 볼 수 있습니다. 셔터 속도가 매우 빠르다는 것을 알 수 있습니다. 즉, 셔터가 1 초의 200 분의 1 초에 열리거나 닫혀서 선명한 이미지를 얻었습니다.
ISO
ISO 계수는 숫자로 측정됩니다. 카메라에 대한 빛의 감도를 나타냅니다. ISO 수치가 낮 으면 카메라가 빛에 덜 민감하다는 의미이고 ISO 수치가 높으면 감도가 높다는 뜻입니다.
효과
ISO가 높을수록 사진이 더 밝아집니다. ISO를 1600으로 설정하면 사진이 매우 밝아지고 그 반대의 경우도 마찬가지입니다.
부작용
ISO가 증가하면 이미지의 노이즈도 증가합니다. 오늘날 대부분의 카메라 제조 회사는 ISO가 더 높은 속도로 설정 될 때 이미지에서 노이즈를 제거하기 위해 노력하고 있습니다.
픽셀
픽셀은 이미지에서 가장 작은 요소입니다. 각 픽셀은 하나의 값에 해당합니다. 8 비트 그레이 스케일 이미지에서 0에서 255 사이의 픽셀 값입니다. 어느 지점에서나 픽셀의 값은 해당 지점에서 치는 광자의 강도에 해당합니다. 각 픽셀은 특정 위치의 빛 강도에 비례하는 값을 저장합니다.
PEL
픽셀은 PEL이라고도합니다. 아래 그림에서 픽셀에 대해 더 많이 이해할 수 있습니다.
위의 그림에는이 이미지를 구성하는 수천 개의 픽셀이있을 수 있습니다. 픽셀 분할을 볼 수있을 정도로 이미지를 확대합니다. 아래 이미지에 나와 있습니다.

위의 그림에는이 이미지를 구성하는 수천 개의 픽셀이있을 수 있습니다. 픽셀 분할을 볼 수있을 정도로 이미지를 확대합니다. 아래 이미지에 나와 있습니다.
CCD 어레이와의 관계 제공
CCD 어레이에서 이미지가 어떻게 형성되는지 살펴 보았습니다. 따라서 픽셀은 다음과 같이 정의 할 수도 있습니다.
CCD 배열의 최소 분할은 픽셀이라고도합니다.
CCD 배열의 각 분할에는 해당 배열에 부딪히는 광자의 강도에 대한 값이 포함됩니다. 이 값은 픽셀이라고도합니다.
총 픽셀 수 계산
이미지를 2 차원 신호 또는 행렬로 정의했습니다. 그런 다음이 경우 PEL의 수는 행 수와 열 수를 곱한 것과 같습니다.
이것은 다음과 같이 수학적으로 표현 될 수 있습니다.
총 픽셀 수 = 행 수 (X) 열 수
또는 (x, y) 좌표 쌍의 수가 총 픽셀 수를 구성한다고 말할 수 있습니다.
컬러 이미지에서 픽셀을 계산하는 방법에 대한 자세한 내용은 이미지 유형 자습서에서 살펴볼 것입니다.
그레이 레벨
어느 지점에서나 픽셀의 값은 해당 위치의 이미지 강도를 나타내며 그레이 레벨이라고도합니다.
이미지 저장소의 픽셀 값과 픽셀 당 비트 자습서에 대해 자세히 살펴 보 겠지만 지금은 픽셀 값이 하나뿐이라는 개념 만 살펴 보겠습니다.
픽셀 값. (0)
이 튜토리얼의 시작 부분에서 이미 정의했듯이 각 픽셀은 하나의 값만 가질 수 있으며 각 값은 이미지의 해당 지점에서 빛의 강도를 나타냅니다.
이제 매우 고유 한 값 0을 살펴 보겠습니다. 값 0은 빛이 없음을 의미합니다. 이는 0이 어둡다는 것을 의미하고, 픽셀이 0의 값을 가질 때마다 그 지점에서 검은 색이 형성됨을 의미합니다.
이 이미지 매트릭스를보세요
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
이제이 이미지 행렬은 모두 0으로 채워져 있습니다. 모든 픽셀의 값은 0입니다.이 행렬을 구성하는 총 픽셀 수를 계산하려면 이렇게해야합니다.
총 픽셀 수 = 총 픽셀 수 행 수 X 총 수 열 수
= 3 X 3
= 9.
이는 이미지가 9 픽셀로 구성되고 해당 이미지의 차원이 3 행 3 열이며 가장 중요한 것은 이미지가 검정색임을 의미합니다.
만들어 질 결과 이미지는 다음과 같습니다.

이제 왜이 이미지가 모두 검은 색입니다. 이미지의 모든 픽셀 값이 0이기 때문입니다.
인간의 눈은 가까이있는 사물을 볼 때 멀리있는 사물에 비해 더 크게 보입니다. 이를 일반적인 방식으로 관점이라고합니다. 변형은 한 상태에서 다른 상태로 객체 등을 전송하는 것입니다.
따라서 전반적으로 원근 변환은 3D 세계를 2D 이미지로 변환하는 작업을 처리합니다. 인간의 시각이 작동하는 원리와 카메라가 작동하는 원리가 같습니다.
왜 이런 일이 발생하는지, 가까이있는 물체는 더 크게 보이며, 멀리있는 물체는 도달했을 때 더 크게 보이지만 더 작아 보입니다.
이 토론은 참조 프레임의 개념으로 시작합니다.
참조 프레임 :
기준 프레임은 기본적으로 우리가 무언가를 측정하는 것과 관련된 일련의 값입니다.
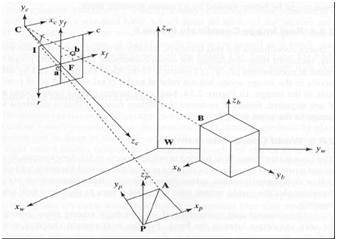
5 개의 기준 프레임
3 차원 세계 / 이미지 / 장면을 분석하기 위해서는 5 개의 서로 다른 참조 프레임이 필요합니다.
Object
World
Camera
Image
Pixel
개체 좌표 프레임
객체 좌표 프레임은 객체 모델링에 사용됩니다. 예를 들어, 특정 개체가 다른 개체와 관련하여 적절한 위치에 있는지 확인합니다. 3D 좌표계입니다.
세계 좌표 프레임
세계 좌표 프레임은 3 차원 세계에서 객체를 상호 연관시키는 데 사용됩니다. 3D 좌표계입니다.
카메라 좌표 프레임
카메라 좌표 프레임은 카메라를 기준으로 개체를 연결하는 데 사용됩니다. 3D 좌표계입니다.
이미지 좌표 프레임
3D 좌표계가 아니라 2D 시스템입니다. 2D 이미지 평면에서 3D 점이 매핑되는 방식을 설명하는 데 사용됩니다.
픽셀 좌표 프레임
또한 2D 좌표계입니다. 각 픽셀에는 픽셀 좌표 값이 있습니다.
이 5 개의 프레임 사이의 변형

이것이 3D 장면이 픽셀 이미지와 함께 2d로 변환되는 방법입니다.
이제이 개념을 수학적으로 설명하겠습니다.
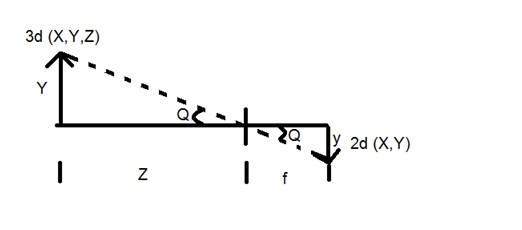
Y = 3D 객체
y = 2d 이미지
f = 카메라의 초점 거리
Z = 이미지와 카메라 사이의 거리
이제이 변환에는 Q로 표시되는 두 개의 다른 각도가 형성됩니다.
첫 번째 각도는
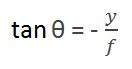
마이너스는 이미지가 반전되었음을 나타냅니다. 형성되는 두 번째 각도는 다음과 같습니다.

이 두 방정식을 비교하면

이 방정식에서 우리는 빛의 광선이 물체에서 쳐진 후 반사되어 카메라에서지나 가면 반전 이미지가 형성됨을 알 수 있습니다.
이 예제를 통해이를 더 잘 이해할 수 있습니다.
예를 들면
형성된 이미지의 크기 계산
키가 5m이고 카메라에서 50m 떨어진 곳에 서있는 사람의 이미지를 촬영했다고 가정하고 초점 거리의 카메라를 사용하여 그 사람의 이미지 크기가 50mm라고 알려야합니다.
해결책:
초점 거리는 mm 단위이므로 계산하려면 모든 것을 mm 단위로 변환해야합니다.
그래서,
Y = 5000mm.
f = 50mm.
Z = 50000mm.
수식에 값을 넣으면
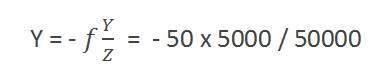
= -5mm.
다시 마이너스 기호는 이미지가 반전되었음을 나타냅니다.
Bpp 또는 픽셀 당 비트는 픽셀 당 비트 수를 나타냅니다. 이미지의 다양한 색상 수는 색상의 깊이 또는 픽셀 당 비트에 따라 다릅니다.
수학의 비트 :
바이너리 비트를 가지고 노는 것과 같습니다.
1 비트로 표현할 수있는 숫자 수입니다.
0
1
얼마나 많은 2 비트 조합을 만들 수 있습니까?
00
01
10
11
bit에서 만들 수있는 총 조합 수를 계산하는 공식을 고안하면 다음과 같습니다.
여기서 bpp는 픽셀 당 비트를 나타냅니다. 2를 얻은 공식에 1을 넣고 2를 공식에 넣으면 4를 얻습니다. 그것은 기하 급수적으로 커집니다.
다른 색상의 수 :
이제 처음에 말했듯이 다른 색상의 수는 픽셀 당 비트 수에 따라 달라집니다.
일부 비트 및 색상에 대한 표는 아래에 나와 있습니다.
| 픽셀 당 비트 | 색상 수 |
|---|---|
| 1bpp | 2 색 |
| 2bpp | 4 색 |
| 3bpp | 8 색 |
| 4bpp | 16 색 |
| 5bpp | 32 색 |
| 6bpp | 64 색 |
| 7bpp | 128 색 |
| 8bpp | 256 색 |
| 10bpp | 1024 색 |
| 16bpp | 65536 색 |
| 24bpp | 16777216 색 (1670 만색) |
| 32bpp | 4294967296 색 (4294 만색) |
이 표는 픽셀 당 다른 비트와 포함 된 색상의 양을 보여줍니다.
음영
지수 성장 패턴을 쉽게 알아 차릴 수 있습니다. 유명한 그레이 스케일 이미지는 8bpp입니다. 즉, 256 가지 색상 또는 256 가지 음영이 있습니다.
음영은 다음과 같이 나타낼 수 있습니다.
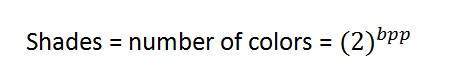
컬러 이미지는 일반적으로 24bpp 형식 또는 16bpp입니다.
이미지 유형 튜토리얼에서 다른 색상 형식 및 이미지 유형에 대해 자세히 알아볼 것입니다.
색상 값 :
검은 색:
화이트 색상 :
흰색을 나타내는 값은 다음과 같이 계산할 수 있습니다.
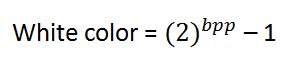
1 bpp의 경우 0은 검정, 1은 흰색을 나타냅니다.
8 bpp 인 경우 0은 검정색, 255는 흰색을 나타냅니다.
회색 색상 :
흑백 색상 값을 계산할 때 회색 색상의 픽셀 값을 계산할 수 있습니다.
회색은 실제로 흑백의 중간 점입니다. 즉,
8bpp의 경우 회색을 나타내는 픽셀 값은 127 또는 128bpp입니다 (0이 아닌 1부터 세는 경우).
이미지 저장 요구 사항
픽셀 당 비트에 대해 논의한 후 이제 이미지의 크기를 계산하는 데 필요한 모든 것이 있습니다.
이미지 크기
이미지의 크기는 세 가지에 따라 달라집니다.
행 수
열 수
픽셀 당 비트 수
크기 계산 공식은 다음과 같습니다.
이미지 크기 = 행 * 열 * bpp
이미지가 있다면 다음과 같이 말하세요.

1024 개의 행과 1024 개의 열이 있다고 가정합니다. 그리고 그것은 회색조 이미지이기 때문에 256 개의 다른 회색 음영이 있거나 픽셀 당 비트 수를가집니다. 그런 다음이 값을 공식에 넣으면
이미지 크기 = 행 * 열 * bpp
= 1024 * 1024 * 8
= 8388608 비트.
그러나 우리가 인식하는 표준 답변이 아니기 때문에 우리의 형식으로 변환 할 것입니다.
그것을 바이트 = 8388608/8 = 1048576 바이트로 변환합니다.
킬로 바이트로 변환 = 1048576 / 1024 = 1024kb.
메가 바이트로 변환 = 1024/1024 = 1Mb.
이것이 이미지 크기가 계산되고 저장되는 방법입니다. 이제 공식에서 이미지의 크기와 픽셀 당 비트 수가 주어지면 이미지가 정사각형 (동일한 행과 동일한 열) 인 경우 이미지의 행과 열을 계산할 수도 있습니다.
다양한 유형의 이미지가 있으며 다양한 유형의 이미지와 색상 분포에 대해 자세히 살펴 보겠습니다.
이진 이미지
이진 이미지는 이름에서 알 수 있듯이 두 개의 픽셀 값만 포함합니다.
0과 1
픽셀 당 비트에 대한 이전 튜토리얼에서 픽셀 값을 각 색상으로 표현하는 방법에 대해 자세히 설명했습니다.
여기서 0은 검은 색을, 1은 흰색을 의미합니다. 모노크롬이라고도합니다.
흑백 이미지 :
따라서 형성된 결과 이미지는 흑백 이미지로만 구성되므로 흑백 이미지라고도합니다.

그레이 레벨 없음
이 바이너리 이미지에 대한 흥미로운 점 중 하나는 그레이 레벨이 없다는 것입니다. 검은 색과 흰색의 두 가지 색상 만 발견됩니다.
체재
바이너리 이미지의 형식은 PBM (Portable bit map)입니다.
2, 3, 4,5,6 비트 색상 형식
색상 형식이 2, 3, 4, 5 및 6 비트 인 이미지는 오늘날 널리 사용되지 않습니다. 그들은 옛날에 오래된 TV 디스플레이 또는 모니터 디스플레이에 사용되었습니다.
그러나 이러한 각 색상은 두 개 이상의 회색 수준을 가지므로 바이너리 이미지와 달리 회색 색상을 갖습니다.
2 비트 4, 3 비트 8, 4 비트 16, 5 비트 32, 6 비트 64에서 서로 다른 색상이 존재합니다.
8 비트 색상 형식
8 비트 색상 형식은 가장 유명한 이미지 형식 중 하나입니다. 256 가지 색상이 있습니다. 일반적으로 그레이 스케일 이미지라고합니다.
8 비트 색상의 범위는 0-255입니다. 여기서 0은 검정, 255는 흰색, 127은 회색을 나타냅니다.
이 형식은 초기에 UNIX 운영 체제의 초기 모델과 초기 컬러 Macintosh에서 사용되었습니다.
아인슈타인의 회색조 이미지는 다음과 같습니다.

체재
이러한 이미지의 형식은 PGM (Portable Gray Map)입니다.
이 형식은 Windows에서 기본적으로 지원되지 않습니다. 그레이 스케일 이미지를 보려면 이미지 뷰어 또는 Matlab과 같은 이미지 처리 도구 상자가 있어야합니다.
그레이 스케일 이미지 뒤에 :
이전 튜토리얼에서 여러 번 설명했듯이 이미지는 2 차원 함수일 뿐이며 2 차원 배열 또는 행렬로 표현할 수 있습니다. 따라서 위에 표시된 아인슈타인 이미지의 경우 뒤에 0에서 255 사이의 값을 갖는 2 차원 행렬이 있습니다.
그러나 그것은 컬러 이미지의 경우가 아닙니다.
16 비트 색상 형식
컬러 이미지 형식입니다. 65,536 가지 색상이 있습니다. 하이 컬러 형식이라고도합니다.
Microsoft에서 8 비트 이상의 색상 형식을 지원하는 시스템에서 사용되었습니다. 이제이 16 비트 형식과 다음 형식에서 24 비트 형식이 모두 색상 형식인지 논의 할 것입니다.
컬러 이미지의 색상 분포는 회색조 이미지만큼 간단하지 않습니다.
16 비트 형식은 실제로 Red, Green 및 Blue의 세 가지 추가 형식으로 나뉩니다. 유명한 (RGB) 형식입니다.
아래 이미지에 그림으로 표현되어 있습니다.
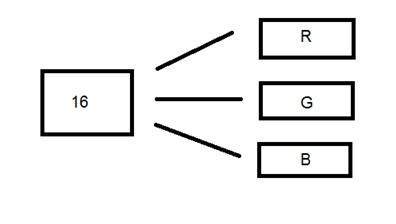
이제 질문이 생깁니다. 16 개를 3 개로 어떻게 분배할까요? 이렇게하면
R의 경우 5 비트, G의 경우 5 비트, B의 경우 5 비트
그런 다음 끝에 하나의 비트가 남아 있습니다.
그래서 16 비트의 분배는 이렇게 이루어졌습니다.
R의 경우 5 비트, G의 경우 6 비트, B의 경우 5 비트.
남겨진 추가 비트가 녹색 비트에 추가됩니다. 녹색은이 세 가지 색상 모두에서 가장 눈을 진정시키는 색상이기 때문입니다.
이것은 배포가 모든 시스템에 뒤 따르는 것은 아닙니다. 일부는 16 비트로 알파 채널을 도입했습니다.
16 비트 형식의 또 다른 분포는 다음과 같습니다.
R의 경우 4 비트, G의 경우 4 비트, B의 경우 4 비트, 알파 채널의 경우 4 비트.
또는 일부는 이렇게 배포합니다
R의 경우 5 비트, G의 경우 5 비트, B의 경우 5 비트, 알파 채널의 경우 1 비트.
24 비트 색상 형식
트루 컬러 형식이라고도하는 24 비트 컬러 형식. 16 비트 색상 형식과 마찬가지로 24 비트 색상 형식에서 24 비트는 Red, Green 및 Blue의 세 가지 다른 형식으로 다시 배포됩니다.
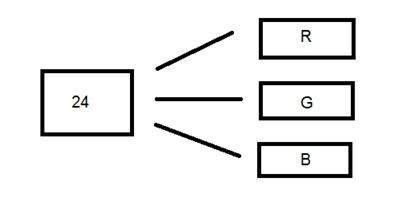
24는 8에서 균등하게 나뉘므로 세 개의 다른 색상 채널간에 균등하게 분배되었습니다.
그들의 분포는 다음과 같습니다.
R의 경우 8 비트, G의 경우 8 비트, B의 경우 8 비트.
24 비트 이미지 뒤에 있습니다.
뒤에 하나의 행렬이있는 8 비트 회색조 영상과 달리 24 비트 영상에는 R, G, B의 3 가지 다른 행렬이 있습니다.

체재
가장 일반적으로 사용되는 형식입니다. 형식은 Linux 운영 체제에서 지원하는 PPM (Portable pixMap)입니다. 유명한 창에는 BMP (Bitmap)라는 자체 형식이 있습니다.
이 튜토리얼에서는 다른 색상을 만들기 위해 다른 색상 코드를 결합하는 방법과 RGB 색상 코드를 16 진수로 또는 그 반대로 변환하는 방법을 알아 봅니다.
다른 색상 코드
여기의 모든 색상은 24 비트 형식입니다. 즉, 각 색상에는 8 비트의 빨간색, 8 비트의 녹색, 8 비트의 파란색이 있습니다. 또는 각 색상에 세 부분이 있다고 말할 수 있습니다. 색상을 만들기 위해이 세 부분의 양을 변경하기 만하면됩니다.
이진 색상 형식
검정색
영상:

소수점 코드 :
(0,0,0)
설명:
이전 자습서에서 설명했듯이 8 비트 형식에서 0은 검정색을 나타냅니다. 그래서 순수한 검은 색을 만들어야한다면 R, G, B의 세 부분을 모두 0으로 만들어야합니다.
색상 : 화이트
영상:

소수점 코드 :
(255,255,255)
설명:
R, G, B의 각 부분은 8 비트 부분이기 때문에. 따라서 8 비트에서 흰색은 255로 구성됩니다. 픽셀 튜토리얼에서 설명합니다. 따라서 흰색을 만들기 위해 각 부분을 255로 설정하고 흰색을 얻었습니다. 각 값을 255로 설정하면 전체 값이 255이며, 이는 색상을 흰색으로 만듭니다.
RGB 색상 모델 :
색상 : 레드
영상:

소수점 코드 :
(255,0,0)
설명:
red color 만 필요하기 때문에 green과 blue 인 나머지 두 부분을 0으로 만들고 red 부분을 최대 값 인 255로 설정합니다.
색상 : 녹색
영상:

소수점 코드 :
(0,255,0)
설명:
녹색 만 필요하므로 나머지 두 부분 인 red 및 blue를 0으로 설정하고 녹색 부분을 최대 값 인 255로 설정합니다.
파란색
영상:

소수점 코드 :
(0,0,255)
설명:
파란색 만 필요하므로 나머지 두 부분 (빨간색과 녹색)을 0으로 설정하고 파란색 부분을 최대 값 인 255로 설정합니다.
회색 색상 :
색깔 : 회색
영상:

소수점 코드 :
(128,128,128)
설명:
pixel 튜토리얼에서 이미 정의했듯이 회색이 실제로 중간 지점입니다. 8 비트 형식에서 중간 지점은 128 또는 127입니다.이 경우에는 128을 선택합니다. 따라서 각 부분을 중간 지점 인 128로 설정하면 전체 중간 값이되고 회색을 얻습니다.
CMYK 색상 모델 :
CMYK는 c는 청록색, m은 자홍색, y는 노란색, k는 검정색을 나타내는 또 다른 색상 모델입니다. CMYK 모델은 일반적으로 두 개의 컬러 카터가 사용되는 컬러 프린터에서 사용됩니다. 하나는 CMY로 구성되고 다른 하나는 검정색으로 구성됩니다.
CMY의 색상은 빨강, 녹색 및 파랑의 양이나 부분을 변경하여 만들 수도 있습니다.
색깔 : 청록색
영상:

소수점 코드 :
(0,255,255)
설명:
청록색은 녹색과 파란색의 두 가지 색상 조합으로 형성됩니다. 그래서 우리는이 두 가지를 최대로 설정하고 빨간색 부분을 0으로 만듭니다. 그리고 우리는 청록색을 얻습니다.
색상 : 마젠타
영상:

소수점 코드 :
(255,0,255)
설명:
마젠타 색상은 빨간색과 파란색의 두 가지 색상 조합으로 형성됩니다. 그래서 우리는이 두 가지를 최대로 설정하고 녹색 부분을 0으로 만듭니다. 그리고 우리는 자홍색을 얻습니다.
색깔 : 황색
영상:

소수점 코드 :
(255,255,0)
설명:
노란색은 빨간색과 녹색의 두 가지 색상의 조합으로 형성됩니다. 그래서 우리는이 두 가지를 최대로 설정하고 파란색 부분을 0으로 만듭니다. 그리고 우리는 노란색을 얻습니다.
변환
이제 색상이 한 형식에서 다른 형식으로 변환되는 방식을 볼 수 있습니다.
RGB에서 16 진 코드로 변환 :
16 진수에서 rgb 로의 변환은 다음 방법을 통해 수행됩니다.
색상을 선택하십시오. 예 : 흰색 = (255, 255, 255).
첫 번째 부분 (예 : 255)을 가져옵니다.
16으로 나눕니다. 이렇게 :
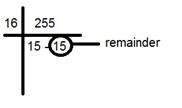
line 아래에있는 두 숫자, factor 및 나머지를 가져옵니다. 이 경우 FF는 15 15입니다.
다음 두 부분에 대해 2 단계를 반복합니다.
모든 16 진 코드를 하나로 결합하십시오.
답변 : #FFFFFF
Hex에서 RGB로 변환 :
16 진 코드에서 rgb 십진 형식으로의 변환은 이런 방식으로 수행됩니다.
16 진수를 가져옵니다. 예 : #FFFFFF
이 숫자를 세 부분으로 나누십시오. FF FF FF
첫 번째 부분을 가져 와서 구성 요소를 분리합니다. FF
각 부분을 개별적으로 바이너리로 변환합니다. (1111) (1111)
이제 개별 바이너리를 하나로 결합합니다. 11111111
이 바이너리를 10 진수로 변환 : 255
이제 2 단계를 두 번 더 반복합니다.
첫 번째 단계의 값은 R, 두 번째 단계는 G, 세 번째 단계는 B에 속합니다.
답 : (255, 255, 255)
일반적인 색상과 16 진수 코드가이 표에 나와 있습니다.
| 색깔 | 16 진수 코드 |
|---|---|
| 검정 | # 000000 |
| 하얀 | #FFFFFF |
| 회색 | # 808080 |
| 빨간 | # FF0000 |
| 초록 | # 00FF00 |
| 푸른 | # 0000FF |
| 청록색 | # 00FFFF |
| 마젠타 | # FF00FF |
| 노랑 | # FFFF00 |
평균 방법
가중 방법 또는 광도 방법
평균 방법
평균 방법이 가장 간단한 방법입니다. 평균 세 가지 색상을 취하면됩니다. RGB 이미지이기 때문에 g와 함께 r을 b에 더한 다음 원하는 회색조 이미지를 얻기 위해 3으로 나눈다는 의미입니다.
이런 식으로 수행됩니다.
그레이 스케일 = (R + G + B) / 3
예를 들면 :

위에 표시된 이미지와 같은 컬러 이미지가 있고 평균 방법을 사용하여 그레이 스케일로 변환하려는 경우. 다음 결과가 나타납니다.

설명
확실히해야 할 한 가지는 원본 작품에 어떤 일이 발생한다는 것입니다. 그것은 우리의 평균적인 방법이 작동한다는 것을 의미합니다. 그러나 결과는 예상과 다릅니다. 이미지를 그레이 스케일로 변환하고 싶었지만 이것은 다소 검은 이미지로 판명되었습니다.
문제
이 문제는 세 가지 색상의 평균을 취한다는 사실 때문에 발생합니다. 세 가지 다른 색상은 세 가지 파장을 가지고 있으며 이미지 형성에 자체 기여도가 있기 때문에 평균 방법을 사용하여 평균적으로 수행하는 것이 아니라 기여도에 따라 평균을 취해야합니다. 지금 우리가하는 것은 이것입니다.
레드 33 %, 그린 33 %, 블루 33 %
우리는 각각의 33 %를 취하고 있습니다. 즉, 각 부분이 이미지에 동일한 기여를합니다. 그러나 실제로는 그렇지 않습니다. 이에 대한 해결책은 광도법에 의해 주어졌습니다.
가중 방법 또는 광도 방법
평균 방법에서 발생하는 문제를 확인했습니다. 가중 방법에는 그 문제에 대한 해결책이 있습니다. 붉은 색은 세 가지 색상 중 파장이 더 많고 녹색은 붉은 색보다 파장이 적을뿐만 아니라 녹색도 눈에 진정 효과를주는 색상입니다.
그것은 우리가 빨간색의 기여도를 줄이고 녹색의 기여도를 높이고이 둘 사이에 파란색 기여도를 넣어야한다는 것을 의미합니다.
따라서 형성되는 새로운 방정식은 다음과 같습니다.
새 회색조 이미지 = ((0.3 * R) + (0.59 * G) + (0.11 * B)).
이 방정식에 따르면 빨간색은 30 %, 녹색은 세 가지 색상 모두에서 더 큰 59 %, 파란색은 11 %를 기여했습니다.
이 방정식을 이미지에 적용하면
원본 이미지 :

그레이 스케일 이미지 :

설명
여기에서 볼 수 있듯이 이미지가 가중치 적용 방법을 사용하여 회색조로 올바르게 변환되었습니다. 평균 방법의 결과에 비해이 이미지는 더 밝습니다.
아날로그 신호를 디지털 신호로 변환 :
대부분의 이미지 센서의 출력은 아날로그 신호이며 저장할 수 없기 때문에 디지털 처리를 적용 할 수 없습니다. 무한한 값을 가질 수있는 신호를 저장하려면 무한한 메모리가 필요하기 때문에 저장할 수 없습니다.
그래서 우리는 아날로그 신호를 디지털 신호로 변환해야합니다.
디지털 이미지를 만들려면 연속 데이터를 디지털 형식으로 은폐해야합니다. 완료되는 두 단계가 있습니다.
Sampling
Quantization
지금 샘플링에 대해 논의하고 양자화는 나중에 논의 할 것이지만 지금은이 두 단계의 차이점과이 두 단계의 필요성에 대해 조금만 논의 할 것입니다.
기본 아이디어 :
아날로그 신호를 디지털 신호로 변환하는 기본 아이디어는

두 축 (x, y)을 모두 디지털 형식으로 변환합니다.
이미지는 좌표 (x 축)뿐만 아니라 진폭 (y 축)에서도 연속적이기 때문에 좌표의 디지털화를 처리하는 부분을 샘플링이라고합니다. 진폭을 디지털화하는 부분을 양자화라고합니다.
견본 추출.
샘플링은 신호 및 시스템 소개 튜토리얼에서 이미 소개되었습니다. 그러나 우리는 여기서 더 논의 할 것입니다.
여기서 우리는 샘플링에 대해 논의했습니다.
샘플링이라는 용어는 샘플을 채취하는 것을 말합니다.
샘플링에서 x 축을 디지털화합니다.
독립 변수에 대해 수행됩니다.
방정식 y = sin (x)의 경우 x 변수에 대해 수행됩니다.
업 샘플링과 다운 샘플링의 두 부분으로 더 나뉩니다.

위의 그림을 보면 신호에 임의의 변동이 있음을 알 수 있습니다. 이러한 변화는 소음 때문입니다. 샘플링에서 우리는 샘플을 취하여이 노이즈를 줄입니다. 더 많은 샘플을 수집하고 이미지의 품질이 더 좋아지고 노이즈가 더 많이 제거되고 그 반대의 경우도 마찬가지입니다.
그러나 x 축에서 샘플링을 수행하면 양자화라고하는 y 축도 샘플링하지 않는 한 신호가 디지털 형식으로 변환되지 않습니다. 더 많은 샘플은 결국 더 많은 데이터를 수집하고 있음을 의미하며 image의 경우 더 많은 픽셀을 의미합니다.
픽셀과의 관계 배
픽셀은 이미지에서 가장 작은 요소이기 때문입니다. 이미지의 총 픽셀 수는 다음과 같이 계산할 수 있습니다.
픽셀 = 총 행 수 * 총 열 수.
총 25 개의 픽셀이 있다고 가정 해 봅시다. 즉, 5 X 5의 정사각형 이미지가 있다는 것을 의미합니다. 그런 다음 위에서 샘플링에서 논의했듯이 더 많은 샘플이 결국 더 많은 픽셀을 생성합니다. 즉, 연속 신호의 x 축에서 25 개의 샘플을 취했습니다. 이는이 이미지의 25 픽셀을 나타냅니다.
이것은 픽셀이 CCD 어레이의 가장 작은 분할이기 때문에 또 다른 결론으로 이어집니다. 그래서 그것은 CCD 배열과도 관계가 있다는 것을 의미합니다. 이것은 이렇게 설명 될 수 있습니다.
CCD 어레이와의 관계
CCD 어레이의 센서 수는 픽셀 수와 직접적으로 동일합니다. 그리고 픽셀 수가 샘플 수와 직접적으로 동일하다는 결론을 내렸기 때문에 샘플 수는 CCD 어레이의 센서 수와 직접적으로 동일합니다.
오버 샘플링.
처음에는 샘플링이 두 가지 유형으로 더 분류된다는 것을 정의했습니다. 업 샘플링과 다운 샘플링입니다. 업 샘플링은 오버 샘플링이라고도합니다.
오버 샘플링은 Zooming으로 알려진 이미지 처리에 매우 깊은 응용 프로그램을 가지고 있습니다.
확대
다음 자습서에서 공식적으로 확대 / 축소를 소개 할 것이지만 지금은 확대 / 축소에 대해 간단히 설명하겠습니다.
확대 / 축소는 픽셀 수를 늘리는 것을 의미하므로 이미지를 확대 할 때 더 자세히 볼 수 있습니다.
픽셀 수의 증가는 오버 샘플링을 통해 이루어집니다. 줌하는 한 가지 방법 또는 샘플을 늘리는 방법은 렌즈의 모터 움직임을 통해 광학적으로 줌한 다음 이미지를 캡처하는 것입니다. 하지만 일단 이미지가 캡처되면해야합니다.
확대 / 축소와 샘플링에는 차이가 있습니다.
개념은 동일합니다. 즉, 샘플을 늘리는 것입니다. 그러나 주요 차이점은 샘플링이 신호에서 수행되는 동안 디지털 이미지에서 확대 / 축소가 수행된다는 것입니다.
픽셀 해상도를 정의하기 전에 픽셀을 정의해야합니다.
픽셀
우리는 픽셀 개념 튜토리얼에서 이미 픽셀을 이미지의 가장 작은 요소로 정의하는 픽셀을 정의했습니다. 또한 픽셀이 특정 위치의 빛 강도에 비례하는 값을 저장할 수 있다고 정의했습니다.
이제 픽셀을 정의 했으므로 해상도를 정의 할 것입니다.
해결
해상도는 여러 가지 방법으로 정의 할 수 있습니다. 픽셀 해상도, 공간 해상도, 시간 해상도, 스펙트럼 해상도 등. 그 중에서 우리는 픽셀 해상도에 대해 논의 할 것입니다.
자신의 컴퓨터 설정에서 모니터 해상도가 800 x 600, 640 x 480 등임을 보셨을 것입니다.
픽셀 해상도에서 해상도라는 용어는 디지털 이미지의 총 픽셀 수를 나타냅니다. 예를 들면. 이미지에 M 개의 행과 N 개의 열이있는 경우 해상도를 MX N으로 정의 할 수 있습니다.
해상도를 총 픽셀 수로 정의하면 픽셀 해상도는 두 숫자 세트로 정의 할 수 있습니다. 첫 번째 숫자는 사진의 너비 또는 열의 픽셀이고 두 번째 숫자는 사진의 높이 또는 너비의 픽셀입니다.
픽셀 해상도가 높을수록 이미지의 품질이 더 높다고 말할 수 있습니다.
이미지의 픽셀 해상도를 4500 X 5500으로 정의 할 수 있습니다.
메가 픽셀
픽셀 해상도를 사용하여 카메라의 메가 픽셀을 계산할 수 있습니다.
열 픽셀 (너비) X 행 픽셀 (높이) / 1 백만.
이미지의 크기는 픽셀 해상도로 정의 할 수 있습니다.
크기 = 픽셀 해상도 X bpp (픽셀 당 비트)
카메라의 메가 픽셀 계산
2500 X 3192 크기의 이미지가 있다고 가정 해 보겠습니다.
픽셀 해상도 = 2500 * 3192 = 7982350 바이트.
100 만 = 7.9 = 8 메가 픽셀 (대략)로 나눕니다.
종횡비
픽셀 해상도의 또 다른 중요한 개념은 종횡비입니다.
종횡비는 이미지 너비와 이미지 높이 사이의 비율입니다. 일반적으로 콜론으로 구분 된 두 숫자 (8 : 9)로 설명됩니다. 이 비율은 이미지와 화면에 따라 다릅니다. 일반적인 종횡비는 다음과 같습니다.
1.33 : 1, 1.37 : 1, 1.43 : 1, 1.50 : 1, 1.56 : 1, 1.66 : 1, 1.75 : 1, 1.78 : 1, 1.85 : 1, 2.00 : 1 등
이점:
가로 세로 비율은 화면에 나타나는 이미지의 균형을 유지합니다. 즉, 가로 및 세로 픽셀 간의 비율을 유지합니다. 종횡비가 증가해도 이미지가 왜곡되지 않습니다.
예를 들면 :
이것은 100 개의 행과 100 개의 열이있는 샘플 이미지입니다. 더 작게 만들고 싶은 경우 품질이 동일하게 유지되거나 다른 방식으로 이미지가 왜곡되지 않는 조건이있는 경우 여기에서 어떻게 발생합니다.
원본 이미지 :

MS 그림판에서 종횡비를 유지하여 행과 열을 변경합니다.
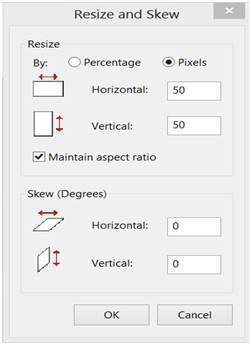
결과

작은 이미지이지만 균형은 동일합니다.
화면 해상도에 따라 비디오를 조정할 수있는 비디오 플레이어에서 종횡비를 보았을 것입니다.
종횡비에서 이미지의 치수 찾기 :
종횡비는 우리에게 많은 것을 알려줍니다. 종횡비를 사용하면 이미지 크기와 함께 이미지 크기를 계산할 수 있습니다.
예를 들면
480000 픽셀의 픽셀 해상도 이미지의 가로 세로 비율이 6 : 2 인 이미지가 주어진 경우 이미지는 그레이 스케일 이미지입니다.
그리고 두 가지를 계산해야합니다.
픽셀 해상도를 해결하여 이미지 크기 계산
이미지의 크기를 계산
해결책:
주어진:
종횡비 : c : r = 6 : 2
픽셀 해상도 : c * r = 480000
픽셀 당 비트 : 회색조 이미지 = 8bpp
찾기:
행 수 =?
열 수 =?
첫 번째 부분 해결 :
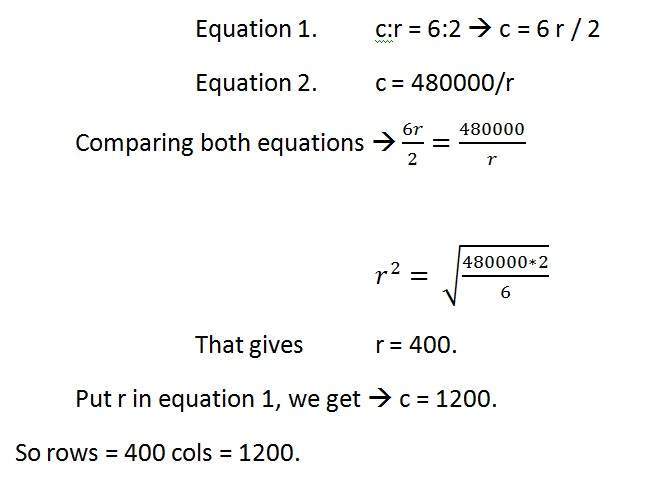
두 번째 부분 해결 :
크기 = 행 * 열 * bpp
이미지 크기 (비트) = 400 * 1200 * 8 = 3840000 비트
이미지 크기 (바이트) = 480000 바이트
이미지 크기 (KB) = 48kb (대략).
이 자습서에서는 확대 / 축소 개념과 이미지 확대 / 축소에 사용되는 일반적인 기술을 소개합니다.
확대
확대 / 축소는 단순히 이미지의 세부 사항이 더 잘 보이고 선명 해졌다는 의미에서 사진을 확대하는 것을 의미합니다. 이미지 확대 / 축소는 카메라 렌즈를 통한 확대 / 축소에서 인터넷에서 이미지 확대 / 축소에 이르기까지 다양한 응용 분야가 있습니다
예를 들면

확대됩니다

두 단계로 확대 할 수 있습니다.
첫 번째 단계는 특정 이미지를 촬영하기 전에 확대 / 축소하는 것입니다. 이를 전처리 줌이라고합니다. 이 확대 / 축소에는 하드웨어 및 기계적 움직임이 포함됩니다.
두 번째 단계는 이미지가 캡처되면 확대 / 축소하는 것입니다. 필요한 부분을 확대하기 위해 픽셀을 조작하는 다양한 알고리즘을 통해 수행됩니다.
다음 튜토리얼에서 자세히 설명하겠습니다.
광학 줌 대 디지털 줌
이 두 가지 유형의 줌이 카메라에서 지원됩니다.
광학 줌 :
광학 줌은 카메라 렌즈의 움직임을 사용하여 이루어집니다. 광학 줌은 실제로 진정한 줌입니다. 광학 줌의 결과는 디지털 줌의 결과보다 훨씬 좋습니다. 광학 줌에서는 이미지의 물체가 카메라에 더 가깝게 보이도록 렌즈에 의해 이미지가 확대됩니다. 광학 줌에서 렌즈는 물리적으로 확장되어 물체를 줌 또는 확대합니다.
전자식 확대:
디지털 줌은 기본적으로 카메라 내의 이미지 처리입니다. 디지털 줌 중에는 이미지의 중앙이 확대되고 사진의 가장자리가 잘립니다. 확대 된 중심으로 인해 물체가 당신에게 더 가까이있는 것처럼 보입니다.
디지털 줌 중에 픽셀이 확장되어 이미지 품질이 저하됩니다.
Photoshop과 같은 이미지 처리 도구 상자 / 소프트웨어를 사용하여 컴퓨터를 통해 이미지를 촬영 한 후에도 동일한 디지털 줌 효과를 볼 수 있습니다.
아래 그림은 아래의 줌 방식 중 하나를 통해 디지털 줌을 한 결과입니다.

이제 우리는 디지털 이미지 처리를 기울이고 있기 때문에 렌즈 나 다른 것을 사용하여 이미지를 광학적으로 확대하는 방법에 초점을 맞추지 않을 것입니다. 오히려 우리는 디지털 이미지를 확대 할 수있는 방법에 초점을 맞출 것입니다.
확대 방법 :
이 작업을 수행하는 많은 방법이 있지만 여기서는 가장 일반적인 방법에 대해 논의 할 것입니다.
아래에 나열되어 있습니다.
픽셀 복제 또는 (최근 접 이웃 보간)
제로 오더 보류 방법
K 배 확대
이 세 가지 방법은 모두 다음 자습서에서 공식적으로 소개됩니다.
이 자습서에서는 확대 / 축소 소개 자습서에서 소개 한 세 가지 확대 / 축소 방법을 공식적으로 소개합니다.
행동 양식
픽셀 복제 또는 (최근 접 이웃 보간)
제로 오더 보류 방법
K 배 확대
각 방법에는 고유 한 장점과 단점이 있습니다. 먼저 픽셀 복제에 대해 설명하겠습니다.
방법 1 : 픽셀 복제 :
소개:
최근 접 이웃 보간이라고도합니다. 이름에서 알 수 있듯이이 방법에서는 인접 픽셀 만 복제합니다. Sampling 튜토리얼에서 이미 논의했듯이 확대 / 축소는 샘플 또는 픽셀의 양을 늘릴뿐입니다. 이 알고리즘은 동일한 원리로 작동합니다.
일:
이 방법에서 우리는 이미 주어진 픽셀로부터 새로운 픽셀을 생성합니다. 각 픽셀은이 방법으로 n 번 행과 열로 복제되며 확대 된 이미지를 얻습니다. 그것만큼 간단합니다.
예를 들면 :
2 행과 2 열의 이미지가 있고 픽셀 복제를 사용하여 두 번 또는 두 번 확대하려면 여기에서 어떻게 할 수 있습니다.
더 나은 이해를 위해 이미지는 이미지의 픽셀 값과 함께 매트릭스 형태로 촬영되었습니다.
| 1 | 2 |
| 삼 | 4 |
위의 이미지에는 두 개의 행과 두 개의 열이 있습니다. 먼저 행으로 확대합니다.
행 현명한 확대 :
row wise를 확대하면 행 픽셀을 인접한 새 셀에 간단히 복사합니다.
여기에서 어떻게되는지.
| 1 | 1 | 2 | 2 |
| 삼 | 삼 | 4 | 4 |
위의 행렬에서 할 수 있듯이 각 픽셀은 행에서 두 번 복제됩니다.
열 크기 확대 :
다음 단계는 각 픽셀 열을 현명하게 복제하는 것입니다. 열 픽셀을 인접한 새 열이나 그 아래에 간단히 복사합니다.
여기에서 어떻게되는지.
| 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 2 |
| 삼 | 삼 | 4 | 4 |
| 삼 | 삼 | 4 | 4 |
새 이미지 크기 :
위의 예에서 알 수 있듯이 2 행 2 열의 원본 이미지는 확대 / 축소 후 4 행 4 열로 변환되었습니다. 즉, 새 이미지의 크기는
(원본 이미지 행 * 확대 / 축소 비율, 원본 이미지 열 * 확대 / 축소 비율)
장점과 단점 :
이 확대 / 축소 기술의 장점 중 하나는 매우 간단하다는 것입니다. 픽셀 만 복사하면됩니다.
이 기술의 단점은 이미지가 확대되었지만 출력이 매우 흐릿하다는 것입니다. 확대 / 축소 비율이 증가함에 따라 이미지가 점점 더 흐려졌습니다. 결국 이미지가 완전히 흐려집니다.
방법 2 : 0 주문 보류
소개
0 차 유지 방법은 확대 / 축소의 또 다른 방법입니다. 두 번 확대 / 축소라고도합니다. 두 번만 확대 할 수 있기 때문입니다. 아래 예제에서 그 이유를 알 수 있습니다.
일
0 차 유지 방법에서는 행에서 인접한 두 요소를 각각 선택한 다음 추가하고 결과를 2로 나누고 그 결과를 두 요소 사이에 배치합니다. 먼저이 행을 현명하게 수행 한 다음이 열을 현명하게 수행합니다.
예를 들면
2 행 2 열의 치수 이미지를 가져 와서 0 차 유지를 사용하여 두 번 확대 해 보겠습니다.
| 1 | 2 |
| 삼 | 4 |
먼저 행 방향으로 확대 한 다음 열 방향으로 확대합니다.
행 현명한 확대
| 1 | 1 | 2 |
| 삼 | 삼 | 4 |
(2 + 1) = 3의 처음 두 숫자를 취한 다음 2로 나누면 1에 가까운 1.5가됩니다. 동일한 방법이 행 2에 적용됩니다.
컬럼 단위 확대
| 1 | 1 | 2 |
| 2 | 2 | 삼 |
| 삼 | 삼 | 4 |
우리는 1과 3 인 두 개의 인접한 열 픽셀 값을 취합니다. 우리는 그것들을 더하고 4를 얻었습니다. 그런 다음 4를 2로 나누고 2를 얻습니다. 모든 열에 동일한 방법이 적용됩니다.
새로운 이미지 크기
보시다시피 새 이미지의 크기는 3 x 3이고 원본 이미지 크기는 2 x 2입니다. 따라서 새 이미지의 크기는 다음 공식을 기반으로합니다.
(2 (행 수)-1) X (2 (열 수)-1)
장점과 단점.
이 확대 / 축소 기술의 장점 중 하나는 가장 가까운 이웃 보간 방법에 비해 흐릿한 그림을 만들지 않는다는 것입니다. 그러나 2의 거듭 제곱으로 만 실행할 수 있다는 단점도 있습니다. 여기서 설명 할 수 있습니다.
두 번 확대 / 축소하는 이유 :
위의 2 행 2 열 이미지를 고려하십시오. 제로 오더 홀드 방법을 사용하여 6 배 확대해야한다면 할 수 없습니다. 공식에서 알 수 있듯이.
2 2,4,8,16,32 등의 거듭 제곱 만 확대 할 수 있습니다.
줌을 시도해도 할 수 없습니다. 처음에 두 번 확대하면 결과는 3x3 크기의 열 현명 확대에 표시된 것과 동일하기 때문입니다. 그런 다음 다시 확대하면 5 x 5와 같은 크기가됩니다. 이제 다시 수행하면 9 x 9와 같은 크기가됩니다.
당신의 공식에 따르면 대답은 11x11이어야합니다. (6 (2)-1) X (6 (2)-1)은 11 x 11을 제공합니다.
방법 3 : K-Times 확대
소개:
K 배는 우리가 논의 할 세 번째 확대 / 축소 방법입니다. 지금까지 논의 된 가장 완벽한 확대 / 축소 알고리즘 중 하나입니다. 두 배 확대 및 픽셀 복제 문제를 모두 해결합니다. 이 확대 / 축소 알고리즘에서 K는 확대 / 축소 계수를 나타냅니다.
일:
이런 식으로 작동합니다.
우선 확대 / 축소에서 두 번했던 것처럼 인접한 두 픽셀을 가져와야합니다. 그런 다음 큰 것에서 작은 것을 빼야합니다. 이 출력 (OP)이라고합니다.
출력 (OP)을 줌 계수 (K)로 나눕니다. 이제 결과를 더 작은 값에 추가하고 결과를 두 값 사이에 넣어야합니다.
방금 입력 한 값에 OP 값을 다시 추가하고 이전에 입력 한 값 옆에 다시 놓습니다. k-1 값을 넣을 때까지해야합니다.
모든 행과 열에 대해 동일한 단계를 반복하면 확대 된 이미지가 표시됩니다.
예를 들면 :
아래에 2 행 3 열의 이미지가 있다고 가정합니다. 그리고 세 번 또는 세 번 확대해야합니다.
| 15 | 30 | 15 |
| 30 | 15 | 30 |
이 경우 K는 3입니다. K = 3.
삽입해야하는 값의 수는 k-1 = 3-1 = 2입니다.
행 현명한 확대
처음 두 개의 인접한 픽셀을 가져옵니다. 15와 30입니다.
30에서 15를 뺍니다. 30-15 = 15.
15를 k로 나눕니다. 15 / k = 15/3 = 5. 우리는 그것을 OP라고 부릅니다. (여기서 op는 이름 일뿐입니다)
낮은 숫자에 OP를 추가합니다. 15 + OP = 15 + 5 = 20.
OP를 20에 다시 추가하십시오. 20 + OP = 20 + 5 = 25.
k-1 값을 삽입해야하므로 두 번 수행합니다.
이제 다음 두 개의 인접한 픽셀에 대해이 단계를 반복합니다. 첫 번째 표에 나와 있습니다.
값을 삽입 한 후 삽입 된 값을 오름차순으로 정렬해야하므로 둘 사이에 대칭이 유지됩니다.
두 번째 표에 나와 있습니다.
1 번 테이블.
| 15 | 20 | 25 | 30 | 20 | 25 | 15 |
| 30 | 20 | 25 | 15 | 20 | 25 | 30 |
표 2.

컬럼 단위 확대
동일한 절차를 컬럼 단위로 수행해야합니다. 절차에는 인접한 두 픽셀 값을 취한 다음 큰 값에서 작은 값을 뺍니다. 그 후에는 그것을 k로 나누어야합니다. 결과를 OP로 저장합니다. 더 작은 OP에 OP를 추가 한 다음 OP에 처음 추가되는 값에 OP를 다시 추가합니다. 새 값을 삽입하십시오.
여기에 당신이 얻은 것이 있습니다.
| 15 | 20 | 25 | 30 | 25 | 20 | 15 |
| 20 | 21 | 21 | 25 | 21 | 21 | 20 |
| 25 | 22 | 22 | 20 | 22 | 22 | 25 |
| 30 | 25 | 20 | 15 | 20 | 25 | 30 |
새로운 이미지 크기
새 이미지의 치수에 대한 공식을 계산하는 가장 좋은 방법은 원본 이미지와 최종 이미지의 치수를 비교하는 것입니다. 원본 이미지의 크기는 2X3이고 새 이미지의 크기는 4x7입니다.
따라서 공식은 다음과 같습니다.
(K (행 수 빼기 1) + 1) X (K (열 수 빼기 1) + 1)
장점과 단점
k time zooming 알고리즘의 분명한 장점 중 하나는 픽셀 복제 알고리즘의 힘이었던 모든 요소의 줌을 계산할 수 있다는 것입니다. 또한 0 차 유지 방법의 힘인 향상된 결과 (덜 흐릿함)를 제공합니다. 따라서 두 알고리즘의 힘을 구성합니다.
이 알고리즘의 유일한 어려움은 마지막에 정렬해야한다는 점입니다. 이는 추가 단계이므로 계산 비용이 증가합니다.
이미지 해상도
이미지 해상도는 다양한 방법으로 정의 할 수 있습니다. 픽셀 해상도 및 종횡비 자습서에서 논의한 픽셀 해상도 중 하나입니다.
이 튜토리얼에서는 공간 해상도라는 또 다른 유형의 해상도를 정의 할 것입니다.
공간 해상도:
공간 해상도는 이미지의 선명도를 픽셀 해상도로 결정할 수 없음을 나타냅니다. 이미지의 픽셀 수는 중요하지 않습니다.
공간 해상도는 다음과 같이 정의 할 수 있습니다.
이미지에서 식별 가능한 가장 작은 세부 사항. (디지털 이미지 처리-Gonzalez, Woods-2nd Edition)
또는 다른 방법으로 공간 해상도를 인치당 독립 픽셀 값의 수로 정의 할 수 있습니다.
요컨대 공간 해상도가 의미하는 것은 두 가지 유형의 이미지를 비교하여 어떤 이미지가 명확한 지 또는 어떤 이미지가 아닌지 확인할 수 없다는 것입니다. 두 이미지를 비교해야한다면 어떤 이미지가 더 선명하거나 공간 해상도가 더 높은지 확인하려면 같은 크기의 두 이미지를 비교해야합니다.
예를 들면 :
이 두 이미지를 비교하여 이미지의 선명도를 확인할 수 없습니다.


두 이미지가 같은 사람이지만 그것이 우리가 판단하는 조건은 아닙니다. 왼쪽 사진은 227 x 222 크기로 축소 된 아인슈타인 사진입니다. 반면 오른쪽 사진은 980 X 749 크기이며 확대 된 이미지입니다. 어느 것이 더 명확한 지 비교하기 위해 비교할 수 없습니다. 이 조건에서는 확대 / 축소 비율이 중요하지 않다는 점을 기억하십시오. 중요한 것은이 두 사진이 동일하지 않다는 것입니다.
따라서 공간 해상도를 측정하기 위해 아래 그림이 목적을 제공합니다.


이제이 두 사진을 비교할 수 있습니다. 두 사진의 크기는 227 X 222입니다. 이제 비교해 보면 왼쪽 사진의 공간 해상도가 더 높거나 오른쪽 사진보다 더 선명하다는 것을 알 수 있습니다. 오른쪽 그림이 흐릿한 이미지이기 때문입니다.
공간 해상도 측정 :
공간 해상도는 선명도를 의미하므로 다른 장치에 대해이를 측정하기 위해 다른 측정이 이루어졌습니다.
예를 들면 :
인치당 도트 수
인치당 라인
인치당 픽셀
이에 대해서는 다음 튜토리얼에서 더 자세히 설명하지만 아래에 간략한 소개 만 있습니다.
인치당 도트 수:
인치당 도트 수 또는 DPI는 일반적으로 모니터에 사용됩니다.
인치당 라인 :
인치당 라인 수 또는 LPI는 일반적으로 레이저 프린터에 사용됩니다.
인치당 픽셀 :
인치당 픽셀 또는 PPI는 태블릿, 휴대 전화 등과 같은 다양한 기기에서 측정됩니다.
공간 해상도에 대한 이전 튜토리얼에서 PPI, DPI, LPI에 대한 간략한 소개에 대해 논의했습니다. 이제 우리는 공식적으로 그들 모두를 논의 할 것입니다.
인치당 픽셀.
픽셀 밀도 또는 인치당 픽셀은 태블릿, 휴대 전화를 포함하는 다양한 기기의 공간 해상도 측정 값입니다.
PPI가 높을수록 품질이 높아집니다. 그것을 더 이해하기 위해 그것이 어떻게 계산되었는지. 휴대폰의 PPI를 계산해 보겠습니다.
삼성 갤럭시 S4의 인치당 픽셀 (PPI) 계산 :

삼성 갤럭시 s4의 PPI 또는 픽셀 밀도는 441입니다. 어떻게 계산할까요?
우선 우리는 픽셀 단위의 대각선 해상도를 계산하기 위해 피타고라스 정리를 할 것입니다.
다음과 같이 주어질 수 있습니다.
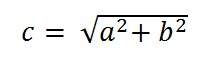
여기서 a와 b는 픽셀 단위의 높이 및 너비 해상도이고 c는 픽셀 단위의 대각선 해상도입니다.
Samsung galaxy s4의 경우 1080 x 1920 픽셀입니다.
따라서 이러한 값을 방정식에 넣으면
C = 2202.90717
이제 우리는 PPI를 계산합니다
PPI = c / 대각선 크기 (인치)
삼선 갤럭시 s4의 대각선 크기는 5.0 인치로 어디에서나 확인할 수 있습니다.
PPI = 2202.90717 / 5.0
PPI = 440.58
PPI = 441 (대략)
즉, 삼성 갤럭시 s4의 픽셀 밀도는 441PPI입니다.
인치당 도트 수.
dpi는 종종 PPI와 관련이 있지만이 둘 사이에는 차이가 있습니다. DPI 또는 dpi는 프린터의 공간 해상도를 측정 한 것입니다. 프린터의 경우 dpi는 프린터에서 이미지가 인쇄 될 때 인치당 인쇄되는 잉크 도트 수를 의미합니다.
각 인치당 픽셀이 인치당 하나의 도트로 인쇄 될 필요는 없습니다. 하나의 픽셀을 인쇄하는 데 사용되는 인치당 도트 수가 많을 수 있습니다. 대부분의 컬러 프린터가 CMYK 모델을 사용하는 이유입니다. 색상이 제한되어 있습니다. 프린터는 픽셀의 색상을 만들기 위해 이러한 색상 중에서 선택해야하는 반면 pc에서는 수십만 색상을 사용할 수 있습니다.
프린터의 dpi가 높을수록 종이에 인쇄 된 문서 또는 이미지의 품질이 높아집니다.
일반적으로 일부 레이저 프린터는 dpi가 300이고 일부는 600 이상입니다.
인치당 라인.
dpi가 인치당 도트 수를 나타내는 경우 인치당 라이너는 인치당 도트 수를 나타냅니다. 하프 톤 스크린의 해상도는 인치당 라인 수로 측정됩니다.
다음 표는 프린터의 인치당 라인 용량 중 일부를 보여줍니다.
| 인쇄기 | LPI |
|---|---|
| 스크린 인쇄 | 45 ~ 65lpi |
| 레이저 프린터 (300dpi) | 65lpi |
| 레이저 프린터 (600dpi) | 85 ~ 105lpi |
| 오프셋 프레스 (신문 용지) | 85lpi |
| 오프셋 프레스 (코팅지) | 85 ~ 185lpi |
이미지 해상도 :
그레이 레벨 해상도 :
그레이 레벨 해상도는 이미지의 음영 또는 그레이 레벨에서 예측 가능하거나 결정적인 변화를 나타냅니다.
짧은 그레이 레벨 해상도는 픽셀 당 비트 수와 같습니다.
픽셀 당 비트 및 이미지 저장 요구 사항에 대한 자습서에서 픽셀 당 비트에 대해 이미 논의했습니다. 여기서는 bpp를 간단히 정의하겠습니다.
BPP :
이미지의 다양한 색상 수는 색상의 깊이 또는 픽셀 당 비트에 따라 다릅니다.
수학적으로 :
그레이 레벨 해상도와 픽셀 당 비트 사이에 설정 될 수있는 수학적 관계는 다음과 같이 주어질 수 있습니다.

이 방정식에서 L은 그레이 레벨의 수를 나타냅니다. 회색 음영으로 정의 할 수도 있습니다. 그리고 k는 bpp 또는 픽셀 당 비트를 나타냅니다. 따라서 픽셀 당 비트 수의 2 승은 그레이 레벨 해상도와 같습니다.
예를 들면 :

위의 아인슈타인 이미지는 그레이 스케일 이미지입니다. 이는 픽셀 당 8 비트 또는 8bpp의 이미지임을 의미합니다.
이제 그레이 레벨 해상도를 계산하려면 여기서 어떻게해야합니다.
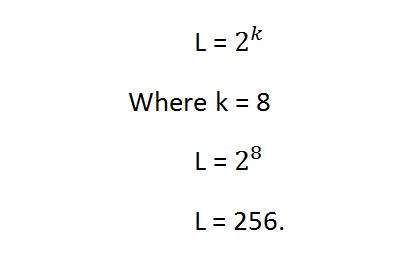
이것은 그레이 레벨 해상도가 256이라는 것을 의미합니다. 또는 다른 방법으로이 이미지에 256 개의 다른 그레이 음영이 있다고 말할 수 있습니다.
이미지의 픽셀 당 비트 수가 많을수록 회색 수준 해상도가 높아집니다.
bpp로 그레이 레벨 해상도 정의 :
그레이 레벨 해상도는 레벨로만 정의 할 필요는 없습니다. 픽셀 당 비트로 정의 할 수도 있습니다.
예를 들면 :
4bpp 이미지가 주어지고 그레이 레벨 해상도를 계산하라는 메시지가 표시됩니다. 그 질문에 대한 답은 두 가지입니다.
첫 번째 대답은 16 단계입니다.
두 번째 대답은 4 비트입니다.
그레이 레벨 해상도에서 bpp 찾기 :
주어진 그레이 레벨 해상도에서 픽셀 당 비트 수를 찾을 수도 있습니다. 이를 위해 우리는 공식을 약간 비틀면됩니다.
방정식 1.

이 공식은 레벨을 찾습니다. 이제 우리가 픽셀 당 비트 또는이 경우 k를 찾으려면 간단히 이렇게 변경합니다.
K = log base 2 (L) 방정식 (2)
첫 번째 방정식에서 레벨 (L)과 픽셀 당 비트 (k) 사이의 관계는 지수 적이기 때문입니다. 이제 우리는 그것을 되돌려 야합니다. 따라서 지수의 역은 로그입니다.
그레이 레벨 해상도에서 픽셀 당 비트를 찾는 예를 들어 보겠습니다.
예를 들면 :
256 레벨의 이미지가 제공되는 경우. 필요한 픽셀 당 비트 수는 얼마입니까?
방정식에 256을 넣으면 얻을 수 있습니다.
K = 밑이 2 인 로그 (256)
K = 8.
따라서 답은 픽셀 당 8 비트입니다.
그레이 레벨 해상도 및 양자화 :
양자화는 다음 튜토리얼에서 공식적으로 소개 될 것이지만 여기서는 그레이 레벨 해상도와 양자화 사이의 관계를 설명 할 것입니다.
그레이 레벨 해상도는 신호의 y 축에서 찾을 수 있습니다. 신호 및 시스템 소개 튜토리얼에서 아날로그 신호를 디지털화하려면 두 단계가 필요하다는 것을 연구했습니다. 샘플링 및 양자화.

샘플링은 x 축에서 수행됩니다. 그리고 양자화는 Y 축에서 이루어집니다.
즉, 이미지의 그레이 레벨 해상도를 디지털화하는 것은 양자화로 수행됩니다.
신호 및 시스템 자습서에서 양자화를 도입했습니다. 이 튜토리얼에서는 공식적으로이를 디지털 이미지와 연관시킬 것입니다. 먼저 양자화에 대해 조금 살펴 보겠습니다.
신호 디지털화.
이전 튜토리얼에서 살펴본 것처럼 아날로그 신호를 디지털로 디지털화하려면 두 가지 기본 단계가 필요합니다. 샘플링 및 양자화. 샘플링은 x 축에서 수행됩니다. x 축 (무한 값)을 디지털 값으로 변환하는 것입니다.
아래 그림은 신호 샘플링을 보여줍니다.

디지털 이미지와 관련된 샘플링 :
샘플링의 개념은 확대 / 축소와 직접 관련이 있습니다. 더 많은 샘플을 취할수록 더 많은 픽셀을 얻을 수 있습니다. 오버 샘플링은 확대 / 축소라고도합니다. 이것은 샘플링 및 확대 / 축소 자습서에서 논의되었습니다.
그러나 신호를 디지털화하는 이야기는 샘플링에서 끝나지 않습니다. 양자화라고하는 또 다른 단계가 있습니다.
양자화 란 무엇입니까?
양자화는 샘플링과 반대입니다. Y 축에서 이루어집니다. 이미지를 qunaitizing 할 때 실제로 신호를 퀀타 (파티션)로 나눕니다.
신호의 x 축에는 좌표 값이 있고 y 축에는 진폭이 있습니다. 따라서 진폭을 디지털화하는 것을 양자화라고합니다.
여기에서 어떻게하는지

이 이미지에서 신호가 세 가지 레벨로 정량화되었음을 알 수 있습니다. 즉, 이미지를 샘플링 할 때 실제로 많은 값을 수집하고 양자화에서 이러한 값으로 레벨을 설정합니다. 이것은 아래 이미지에서 더 명확 할 수 있습니다.
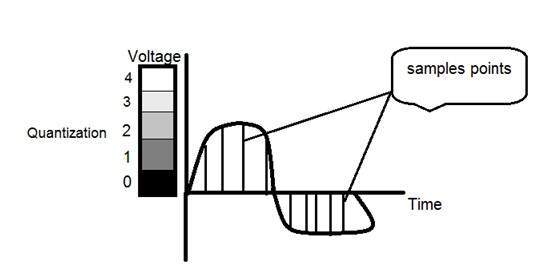
샘플링에 표시된 그림에서는 샘플이 취해졌지만 여전히 연속적인 그레이 레벨 값 범위까지 수직으로 확장되었습니다. 위의 그림에서 이러한 수직 범위 값은 5 개의 다른 레벨 또는 파티션으로 양자화되었습니다. 0 블랙에서 4 화이트까지 다양합니다. 이 수준은 원하는 이미지 유형에 따라 다를 수 있습니다.
그레이 레벨과 양자화의 관계는 아래에서 더 논의되었습니다.
그레이 레벨 해상도와 양자화의 관계 :
위에 표시된 양자화 된 그림에는 5 가지 수준의 회색이 있습니다. 이는이 신호에서 형성된 이미지가 5 가지 색상 만 가질 수 있음을 의미합니다. 약간의 회색 색상이있는 흑백 이미지입니다. 이제 이미지의 품질을 더 좋게 만들려면 여기서 할 수있는 한 가지가 있습니다. 즉, 레벨을 높이거나 그레이 레벨 해상도를 높입니다. 이 수준을 256으로 늘리면 회색조 이미지가 있음을 의미합니다. 단순한 흑백 이미지보다 훨씬 낫습니다.
이제 256 또는 5 또는 선택한 수준을 회색 수준이라고합니다. 이전 그레이 레벨 해상도 튜토리얼에서 논의한 공식을 기억하십시오.

그레이 레벨은 두 가지 방법으로 정의 할 수 있습니다. 이 둘은 어느 것입니다.
그레이 레벨 = 픽셀 당 비트 수 (BPP) (방정식에서 k)
그레이 레벨 = 픽셀 당 레벨 수.
이 경우 그레이 레벨은 256입니다. 비트 수를 계산해야한다면 방정식에 값을 입력하면됩니다. 256levels의 경우 256 개의 다른 회색 음영과 픽셀 당 8 비트가 있으므로 이미지는 회색조 이미지가됩니다.
그레이 레벨 줄이기
이제 이미지에 미치는 영향을보기 위해 이미지의 회색 수준을 줄입니다.
예를 들면 :
256 개의 서로 다른 레벨을 가진 8bpp의 이미지가 있다고 가정 해 보겠습니다. 회색조 이미지이며 이미지는 다음과 같습니다.
256 그레이 레벨

이제 그레이 레벨을 줄이기 시작합니다. 먼저 회색 수준을 256에서 128로 줄입니다.
128 그레이 레벨

그레이 레벨을 절반으로 줄인 후에는 이미지에 큰 영향을주지 않습니다. 좀 더 줄 이겠습니다.
64 그레이 레벨

여전히 효과가 많지 않은 경우 레벨을 더 낮출 수 있습니다.
32 그레이 레벨

여전히 약간의 효과가 있다는 것을보고 놀랐습니다. 이유 때문일 수 있습니다. 그것이 아인슈타인의 그림이기 때문일 수 있지만 수준을 더 낮출 수 있습니다.
16 그레이 레벨

여기 붐, 우리가 간다. 이미지는 마침내 레벨에 의해 영향을 받는다는 것을 드러낸다.
8 그레이 레벨

4 그레이 레벨

이제 축소하기 전에 2 단계를 더 추가하면 회색 수준을 줄임으로써 이미지가 심하게 왜곡되었음을 쉽게 확인할 수 있습니다. 이제 우리는 단순한 흑백 레벨에 불과한 2 레벨로 줄일 것입니다. 이미지가 단순한 흑백 이미지임을 의미합니다.
2 그레이 레벨

이것이 우리가 달성 할 수있는 마지막 수준입니다. 더 줄이면 해석 할 수없는 단순한 검은 색 이미지가되기 때문입니다.
윤곽 :
여기에 흥미로운 관찰이 있습니다. 그레이 레벨 수를 줄이면 이미지에 특별한 유형의 효과 시작이 나타나며, 이는 16 그레이 레벨 사진에서 명확하게 볼 수 있습니다. 이 효과를 컨투어링이라고합니다.
ISO 기본 설정 곡선 :
이 효과에 대한 답, 그것이 나타나는 이유는 Iso 선호도 곡선에 있습니다. Contouring 및 Iso 기본 설정 곡선에 대한 다음 자습서에서 설명합니다.
컨투어링이란?
이미지의 회색 수준 수를 줄이면 일부 잘못된 색상 또는 가장자리가 이미지에 나타나기 시작합니다. 이것은 양자화의 마지막 튜토리얼에서 보여졌습니다.
한번 살펴 보겠습니다.
256 개의 다른 음영 또는 회색 레벨을 가진 8bpp (회색조 이미지)의 이미지가 있다고 가정 해 보겠습니다.

위의 사진에는 256 가지의 회색 음영이 있습니다. 이제 128로 줄이고 64로 더 줄이면 이미지가 거의 동일합니다. 하지만 다시 32 단계로 줄이면 다음과 같은 그림이 나옵니다.

자세히 살펴보면 이미지에 효과가 나타나기 시작하는 것을 알 수 있습니다. 이러한 효과는 16 단계로 더 줄이면 더 잘 보입니다.

이 이미지에 나타나기 시작하는 이러한 선은 위 이미지에서 매우 잘 보이는 윤곽선으로 알려져 있습니다.
컨투어링 증가 및 감소
컨투어링의 효과는 그레이 레벨의 수를 줄이면 증가하고 그레이 레벨의 수를 늘리면 효과가 감소합니다. 둘 다 그 반대입니다.

VS

이는 더 많은 양자화를 의미하고 더 많은 컨투어링에 영향을 미치며 그 반대도 마찬가지입니다. 하지만 항상 그렇습니다. 대답은 아니오입니다. 이는 아래에서 설명하는 다른 사항에 따라 다릅니다.
등위 곡선
그레이 레벨과 컨투어링의이 효과에 대해 수행 된 연구 결과는 Iso 선호 곡선으로 알려진 곡선 형태로 그래프에 표시되었습니다.
Isopreference 곡선의 현상은 윤곽선의 효과가 그레이 레벨 해상도 감소뿐만 아니라 이미지 세부 사항에도 의존한다는 것을 보여줍니다.
연구의 본질은 다음과 같습니다.
이미지의 디테일이 더 많으면 그레이 레벨이 양자화 될 때 디테일이 덜한 이미지와 비교하여 윤곽 효과가 나중에이 이미지에 나타나기 시작합니다.
원래 연구에 따르면 연구원들은이 세 가지 이미지를 촬영했으며 세 이미지 모두에서 그레이 레벨 해상도를 변경했습니다.
이미지는



디테일의 정도:
첫 번째 이미지에는 얼굴 만 있으므로 세부 정보가 매우 적습니다. 두 번째 이미지에는 카메라맨, 그의 카메라, 카메라 스탠드 및 배경 개체 등과 같은 이미지의 다른 개체도 포함되어 있지만 세 번째 이미지에는 다른 모든 이미지보다 더 많은 세부 정보가 있습니다.
실험:
그레이 레벨 해상도는 모든 이미지에서 다양했으며 청중은이 세 이미지를 주관적으로 평가하도록 요청 받았습니다. 평가 후 결과에 따라 그래프가 그려졌습니다.
결과:
결과는 그래프에 그려졌습니다. 그래프의 각 곡선은 하나의 이미지를 나타냅니다. x 축의 값은 그레이 레벨의 수를 나타내고 y 축의 값은 픽셀 당 비트 (k)를 나타냅니다.
그래프는 아래와 같습니다.
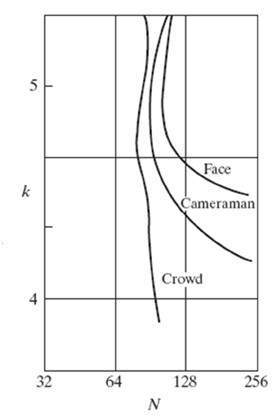
이 그래프에 따르면 얼굴이었던 첫 번째 이미지가 다른 두 이미지보다 일찍 윤곽이 잡 혔음을 알 수 있습니다. 카메라맨의 두 번째 이미지는 첫 번째 이미지의 그레이 레벨이 감소한 후 약간 윤곽이 잡혔습니다. 첫 번째 이미지보다 더 많은 세부 정보가 있기 때문입니다. 그리고 세 번째 이미지는 처음 두 이미지, 즉 4bpp 이후에 많은 윤곽을 잡았습니다. ,이 이미지에 자세한 내용이 있기 때문입니다.
결론:
따라서 더 자세한 이미지의 경우 등위 곡선이 점점 더 수직이됩니다. 또한 디테일이 많은 이미지의 경우 그레이 레벨이 거의 필요하지 않습니다.
Quantization 및 Contouring의 마지막 두 자습서에서 이미지의 회색 수준을 줄이면 이미지를 표시하는 데 필요한 색상 수가 줄어드는 것을 확인했습니다. 그레이 레벨이 2 2 감소하면 나타나는 이미지가 공간 해상도가 많지 않거나 그다지 매력적이지 않습니다.
디더링 :
디더링은 실제로 존재하지 않는 색상의 환상을 만드는 과정입니다. 이것은 임의의 픽셀 배열로 이루어집니다.
예를 들면. 이 이미지를 고려하십시오.

흑백 픽셀 만있는 이미지입니다. 픽셀은 아래에 표시된 다른 이미지를 형성하기 위해 순서대로 배열됩니다. 픽셀 배열이 변경되었지만 픽셀 수는 변경되지 않았습니다.

왜 디더링인가?
디더링이 필요한 이유는 양자화와의 관계에 있습니다.
양자화를 통한 디더링.
양자화를 수행하면 마지막 수준까지 마지막 수준 (수준 2)에 들어오는 이미지가 다음과 같은 것을 볼 수 있습니다.

이제 여기 이미지에서 볼 수 있듯이 그림이 명확하지 않습니다. 특히 아인슈타인 이미지의 왼쪽 팔과 뒷면을 보면 더욱 그렇습니다. 또한이 사진에는 아인슈타인에 대한 정보 나 세부 사항이 많지 않습니다.
이제이 이미지를 좀 더 세부적인 이미지로 변경하려면 디더링을 수행해야합니다.
디더링을 수행합니다.
우선, 우리는 임계 값에 대해 작업 할 것입니다. 디더링은 일반적으로 임계 값을 개선하기 위해 작동합니다. 임계 값을 설정하는 동안 이미지에서 그라디언트가 부드러운 곳에 날카로운 가장자리가 나타납니다.
임계 값에서 우리는 단순히 상수 값을 선택합니다. 해당 값 위의 모든 픽셀은 1로 간주되고 그 아래의 모든 값은 0으로 간주됩니다.
임계 값 이후에이 이미지를 얻었습니다.

이 이미지의 값은 이미 0과 1 또는 흑백이므로 이미지에 큰 변화가 없기 때문입니다.
이제 임의의 디더링을 수행합니다. 임의의 픽셀 배열.

우리는 더 많은 세부 사항을 조금 더 제공하는 이미지를 얻었지만 그 대비가 매우 낮습니다.
그래서 우리는 콘트라스트를 증가시킬 더 많은 디더링을합니다. 우리가 얻은 이미지는 다음과 같습니다.

이제 임의 디더링 개념과 임계 값을 혼합하여 이와 같은 이미지를 얻었습니다.

이제 보시다시피 이미지의 픽셀을 다시 정렬하여 모든 이미지를 얻었습니다. 이 재 배열은 임의적이거나 일부 측정에 따를 수 있습니다.
이미지 처리에서 히스토그램 사용에 대해 논의하기 전에 먼저 히스토그램이 무엇인지, 어떻게 사용되는지 살펴본 다음 히스토그램의 예를 살펴보면서 히스토그램을 더 잘 이해할 수 있습니다.
히스토그램 :
히스토그램은 그래프입니다. 어떤 것의 빈도를 보여주는 그래프. 일반적으로 히스토그램에는 전체 데이터 세트에서 데이터 발생 빈도를 나타내는 막대가 있습니다.
히스토그램에는 x 축과 y 축의 두 축이 있습니다.
x 축에는 빈도를 계산해야하는 이벤트가 포함됩니다.
y 축은 주파수를 포함합니다.
막대의 높이가 다르면 데이터 발생 빈도가 다릅니다.
일반적으로 히스토그램은 다음과 같습니다.
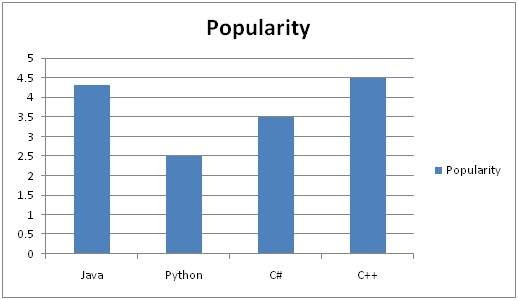
이제이 히스토그램의 예가 build
예:
프로그래밍 학생 클래스를 고려하고 당신은 그들에게 파이썬을 가르치고 있습니다.
학기 말에 표에 표시된 결과를 얻었습니다. 그러나 그것은 매우 지저분하고 수업의 전반적인 결과를 보여주지 않습니다. 따라서 결과에 대한 히스토그램을 작성하여 수업에서 전체 성적 발생 빈도를 표시해야합니다. 여기서 어떻게 할 것인가.
결과 지 :
| 이름 | 등급 |
|---|---|
| 남자 | ㅏ |
| 잭 | 디 |
| 카터 | 비 |
| 나사 돌리개 | ㅏ |
| 리사 | C + |
| 데릭 | ㅏ- |
| 톰 | B + |
결과 시트의 히스토그램 :
이제 여러분이하려는 것은 x와 y 축에 무엇이 오는지 찾아야한다는 것입니다.
확실히해야 할 것은 y 축에 주파수가 포함되어 있다는 것입니다. X 축에는 빈도를 계산해야하는 이벤트가 포함됩니다. 이 경우 x 축에는 등급이 포함됩니다.
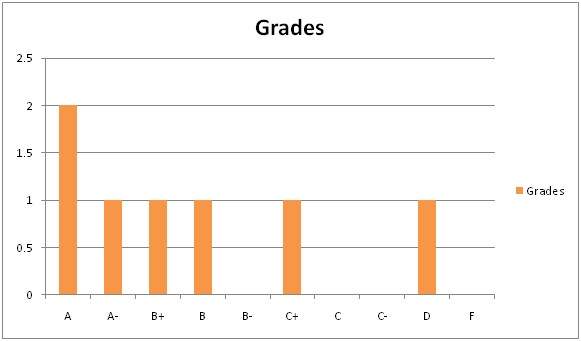
이제 이미지에서 히스토그램을 어떻게 사용합니까?
이미지의 히스토그램
다른 히스토그램과 마찬가지로 이미지의 히스토그램도 빈도를 보여줍니다. 그러나 이미지 히스토그램은 픽셀 강도 값의 빈도를 보여줍니다. 이미지 히스토그램에서 x 축은 그레이 레벨 강도를 나타내고 y 축은 이러한 강도의 빈도를 나타냅니다.
예를 들면 :

위의 아인슈타인 사진의 히스토그램은 다음과 같습니다.
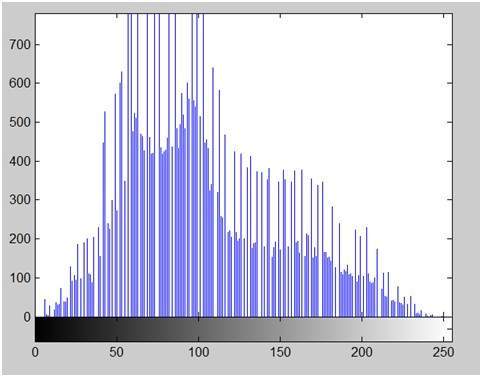
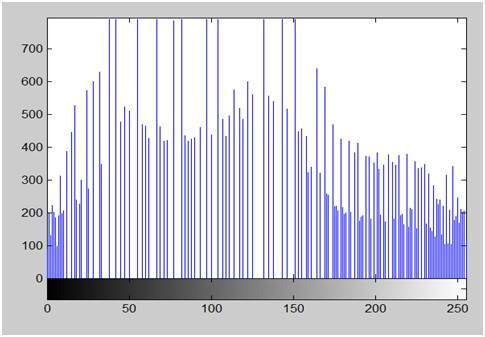
히스토그램의 x 축은 픽셀 값의 범위를 보여줍니다. 8bpp 이미지이므로 256 단계의 회색 또는 회색 음영이 있음을 의미합니다. 이것이 x 축의 범위가 0에서 시작하여 255에서 50의 간격으로 끝나는 이유입니다. 반면에 y 축은 이러한 강도의 개수입니다.
그래프에서 볼 수 있듯이, 빈도가 높은 막대의 대부분은 더 어두운 부분 인 전반부에 있습니다. 그것은 우리가 얻은 이미지가 더 어둡다는 것을 의미합니다. 그리고 이것은 이미지에서도 증명 될 수 있습니다.
히스토그램의 응용 :
히스토그램은 이미지 처리에 많이 사용됩니다. 위에서 논의한 첫 번째 용도는 이미지 분석입니다. 히스토그램 만보고 이미지에 대해 예측할 수 있습니다. 몸의 뼈의 엑스레이를 보는 것과 같습니다.
히스토그램의 두 번째 용도는 밝기 목적입니다. 히스토그램은 이미지 밝기에 광범위하게 적용됩니다. 밝기뿐만 아니라 히스토그램도 이미지의 대비를 조정하는 데 사용됩니다.
히스토그램의 또 다른 중요한 용도는 이미지를 균등화하는 것입니다.
마지막으로 히스토그램은 임계 값에 광범위하게 사용됩니다. 이것은 주로 컴퓨터 비전에서 사용됩니다.
명도:
밝기는 상대적인 용어입니다. 그것은 당신의 시각적 인식에 달려 있습니다. 밝기는 상대적인 용어이므로 밝기는 우리가 비교하는 광원에 대한 광원의 에너지 출력량으로 정의 할 수 있습니다. 어떤 경우에는 이미지가 밝고 어떤 경우에는 인식하기 쉽지 않다고 쉽게 말할 수 있습니다.
예를 들면 :
이 두 이미지를 모두 살펴보고 어느 것이 더 밝은 지 비교하십시오.

왼쪽 이미지에 비해 오른쪽 이미지가 더 밝다는 것을 쉽게 알 수 있습니다.
그러나 오른쪽 이미지가 첫 번째 이미지보다 더 어둡게 만들어지면 왼쪽 이미지가 왼쪽 이미지보다 더 밝다고 말할 수 있습니다.
이미지를 더 밝게 만드는 방법.
밝기는 이미지 매트릭스에 간단한 더하기 또는 빼기로 간단히 늘리거나 줄일 수 있습니다.
5 행 5 열의 검은 색 이미지를 생각해보세요

이미 알고 있으므로 각 이미지에는 픽셀 값을 포함하는 행렬이 뒤에 있습니다. 이 이미지 매트릭스는 아래와 같습니다.
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
전체 행렬이 0으로 채워지고 이미지가 훨씬 더 어둡기 때문입니다.
이제 다른 동일한 검은 색 이미지와 비교하여이 이미지가 더 밝아 졌는지 여부를 확인합니다.

여전히 두 이미지가 동일합니다. 이제 image1에 대해 몇 가지 작업을 수행하여 두 번째 이미지보다 더 밝아집니다.
우리가 할 일은 단순히 이미지 1의 각 행렬 값에 1의 값을 추가하는 것입니다. 이미지 1을 추가 한 후에는 다음과 같습니다.

이제 다시 이미지 2와 비교하여 차이점을 확인합니다.

두 이미지가 똑같이 보이기 때문에 어느 이미지가 더 밝은 지 알 수 없습니다.
이제 우리가 할 것은 이미지 1의 각 행렬 값에 50을 더하고 이미지가 어떻게되었는지 확인하는 것입니다.
출력은 다음과 같습니다.

이제 다시 이미지 2와 비교할 것입니다.
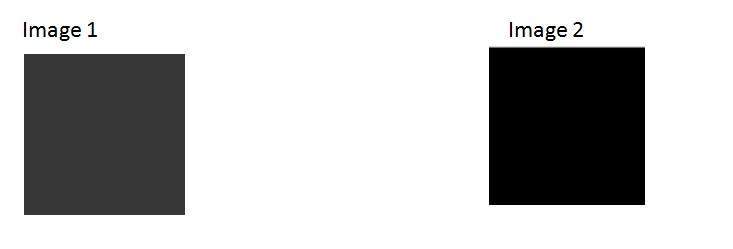
이제 이미지 1이 이미지 2보다 약간 더 밝다는 것을 알 수 있습니다. 계속해서 이미지 1 매트릭스에 45 값을 더하고 이번에는 두 이미지를 다시 비교합니다.

이제 비교해 보면이 이미지 1이 이미지 2보다 분명히 더 밝다는 것을 알 수 있습니다.
예전 이미지보다 더 밝다 1. 이 시점에서 image1의 행렬은 먼저 5를 더한 다음 50, 45를 더할 때 각 인덱스에 100을 포함합니다. 따라서 5 + 50 + 45 = 100입니다.
대조
대비는 이미지의 최대 픽셀 강도와 최소 픽셀 강도의 차이로 간단히 설명 할 수 있습니다.
예를 들면.
밝기의 최종 이미지 1를 고려하십시오.

이 이미지의 매트릭스는 다음과 같습니다.
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
이 행렬의 최대 값은 100입니다.
이 행렬의 최소값은 100입니다.
대비 = 최대 픽셀 강도 (빼기) 최소 픽셀 강도
= 100 (빼기) 100
= 0
0은이 이미지의 대비가 0임을 의미합니다.
논의하기 전에 이미지 변환이 무엇인지, 변환이 무엇인지 논의 할 것입니다.
변환.
변환은 기능입니다. 일부 작업을 수행 한 후 한 세트를 다른 세트로 매핑하는 기능입니다.
디지털 이미지 처리 시스템 :
우리는 이미 입문 튜토리얼에서 디지털 이미지 처리에서 입력이 이미지이고 출력이 이미지가되는 시스템을 개발할 것임을 이미 보았습니다. 그리고 시스템은 입력 이미지에 대해 일부 처리를 수행하고 처리 된 이미지로 출력을 제공합니다. 아래와 같습니다.
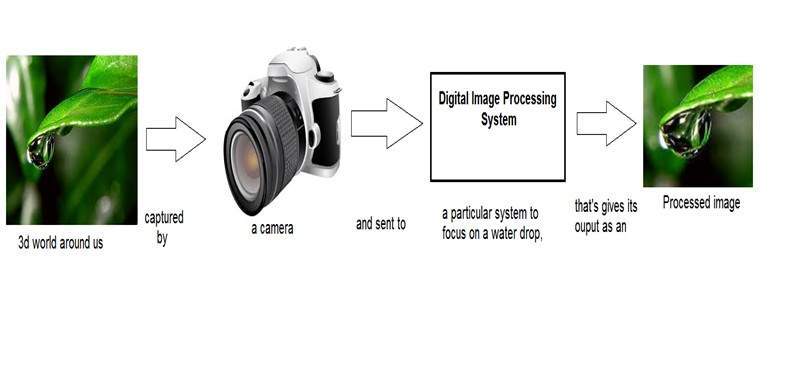
이제이 디지털 시스템 내부에 적용된 이미지를 처리하여 출력으로 변환하는 기능을 변환 기능이라고 할 수 있습니다.
변환 또는 관계를 보여 주므로 image1이 image2로 변환되는 방식입니다.
이미지 변환.
이 방정식을 고려하십시오
G (x, y) = T {f (x, y)}
이 방정식에서
F (x, y) = 변환 함수를 적용해야하는 입력 이미지.
G (x, y) = 출력 이미지 또는 처리 된 이미지.
T는 변환 함수입니다.
입력 이미지와 처리 된 출력 이미지 간의 이러한 관계는 다음과 같이 나타낼 수도 있습니다.
s = T (r)
여기서 r은 실제로 모든 지점에서 f (x, y)의 픽셀 값 또는 회색 수준 강도입니다. 그리고 s는 어느 지점에서나 g (x, y)의 픽셀 값 또는 그레이 레벨 강도입니다.
기본 그레이 레벨 변환은 기본 그레이 레벨 변환 튜토리얼에서 논의되었습니다.
이제 우리는 매우 기본적인 변형 함수에 대해 논의 할 것입니다.
예 :
이 변환 함수를 고려하십시오.
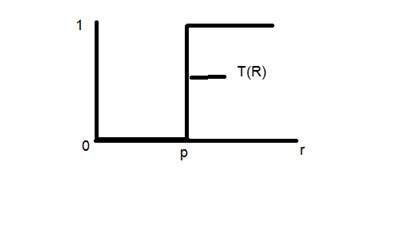
포인트 r을 256으로, 포인트 p를 127로 설정합니다.이 이미지를 1bpp 이미지로 간주합니다. 즉, 0과 1 인 두 수준의 강도 만 있습니다. 따라서이 경우 그래프에 표시된 변환은 다음과 같이 설명 될 수 있습니다.
127 (포인트 p) 미만의 모든 픽셀 강도 값은 0이며 검은 색을 의미합니다. 그리고 127보다 큰 모든 픽셀 강도 값은 1입니다. 즉, 흰색을 의미합니다. 하지만 정확한 127 점에서 갑작스런 전송 변화가 있기 때문에 정확한 지점에서 값이 0 또는 1이 될 것이라고 말할 수 없습니다.
수학적으로이 변환 함수는 다음과 같이 표시 될 수 있습니다.
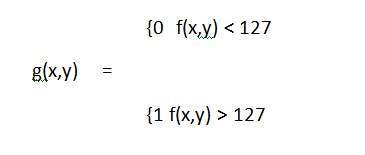
다음과 같은 또 다른 변환을 고려하십시오.
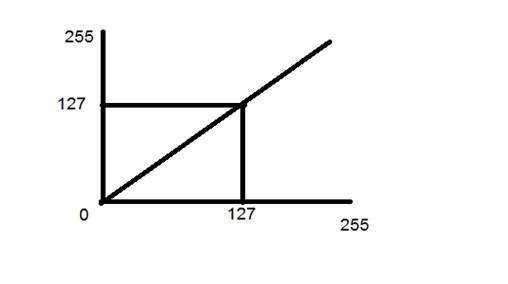
이제이 특정 그래프를 보면 입력 이미지와 출력 이미지 사이에 직선 전환선이 표시됩니다.
각 픽셀 또는 입력 이미지의 강도 값에 대해 출력 이미지의 강도 값이 동일 함을 보여줍니다. 이는 출력 이미지가 입력 이미지의 정확한 복제본임을 의미합니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
g (x, y) = f (x, y)
이 경우 입력 및 출력 이미지는 아래와 같습니다.

히스토그램의 기본 개념은 히스토그램 소개 튜토리얼에서 논의되었습니다. 그러나 여기서는 히스토그램을 간략하게 소개하겠습니다.
히스토그램 :
히스토그램은 데이터 발생 빈도를 보여주는 그래프 일뿐입니다. 히스토그램은 이미지 처리에 많이 사용되며 여기서 히스토그램 슬라이딩이라고하는 한 사용자에 대해 논의 할 것입니다.
히스토그램 슬라이딩.
히스토그램 슬라이딩에서는 전체 히스토그램을 오른쪽 또는 왼쪽으로 간단히 이동합니다. 히스토그램이 오른쪽 또는 왼쪽으로 이동하거나 미끄러지기 때문에 이미지에서 명확한 변화를 볼 수 있습니다.이 자습서에서는 밝기를 조작하기 위해 히스토그램 슬라이딩을 사용합니다.
용어 즉 : 밝기는 밝기 및 대비에 대한 소개 튜토리얼에서 논의되었습니다. 그러나 우리는 여기서 간단히 정의 할 것입니다.
명도:
밝기는 상대적인 용어입니다. 밝기는 특정 광원에서 방출되는 빛의 강도로 정의 할 수 있습니다.
대조:
대비는 이미지의 최대 픽셀 강도와 최소 픽셀 강도의 차이로 정의 할 수 있습니다.
슬라이딩 히스토그램
히스토그램 슬라이딩을 사용하여 밝기 증가

이 이미지의 히스토그램은 아래와 같습니다.
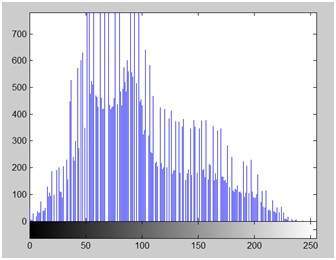
이 히스토그램의 y 축에는 빈도 또는 개수가 있습니다. 그리고 x 축에는 그레이 레벨 값이 있습니다. 위의 히스토그램에서 볼 수 있듯이 카운트가 700 이상인 그레이 레벨 강도는 전반부 부분에 있으며 더 검은 부분을 의미합니다. 그래서 우리는 좀 더 어두운 이미지를 얻었습니다.
밝기를 높이기 위해 히스토그램을 오른쪽 또는 흰색 부분으로 슬라이드합니다. 이렇게하려면이 이미지에 최소한 50의 값을 추가해야합니다. 위의 히스토그램에서 볼 수 있기 때문에이 이미지에는 순수한 검정색 인 0 픽셀 강도가 있습니다. 따라서 0에서 50을 더하면 0 강도에있는 모든 값을 50 강도로 이동하고 나머지 모든 값은 그에 따라 이동합니다.
해보자.
여기에 각 픽셀 강도에 50을 더한 결과가 있습니다.
이미지는 아래와 같습니다.

그리고 그 히스토그램은 아래와 같습니다.
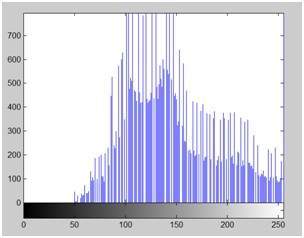
이 두 이미지와 히스토그램을 비교하여 어떤 변화가 있는지 살펴 보겠습니다.
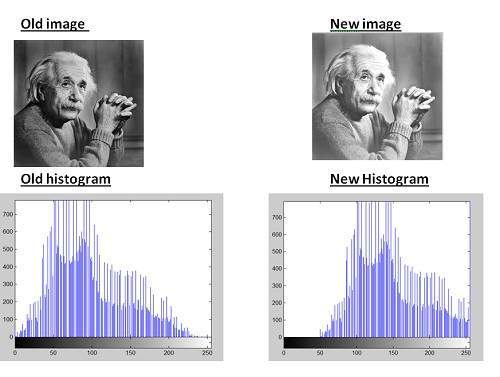
결론:
새 히스토그램에서 알 수 있듯이 모든 픽셀 값이 오른쪽으로 이동했으며 그 효과는 새 이미지에서 볼 수 있습니다.
히스토그램 슬라이딩을 사용하여 밝기 감소
이제 이전 이미지가 더 밝게 보일 정도로 새 이미지의 밝기를 줄이려면 새 이미지의 모든 매트릭스에서 일부 값을 빼야합니다. 뺄 값은 80입니다. 이미 원본 이미지에 50을 더하고 더 밝은 이미지를 얻었으므로 이제 더 어둡게 만들려면 적어도 50 개 이상을 빼야합니다.
그리고 이것은 우리가 새로운 이미지에서 80을 뺀 후에 얻은 것입니다.
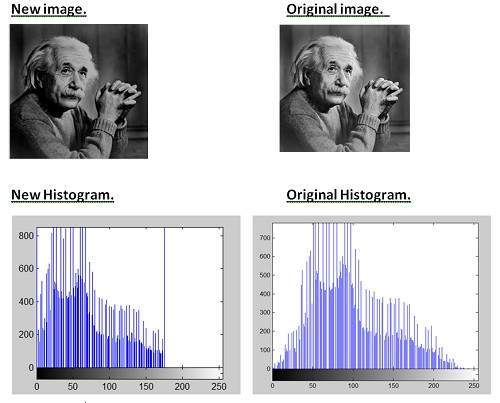
결론:
새 이미지의 히스토그램에서 모든 픽셀 값이 오른쪽으로 이동했음을 알 수 있으므로 새 이미지가 더 어둡고 이제 원본 이미지가이 새 이미지와 비교하여 더 밝게 보이는 이미지에서 확인할 수 있습니다.
히스토그램 소개 튜토리얼에서 논의한 히스토그램의 다른 장점 중 하나는 대비 향상입니다.
대비를 높이는 방법에는 두 가지가 있습니다. 첫 번째는 대비를 높이는 히스토그램 스트레칭입니다. 두 번째는 대비를 강화하는 히스토그램 이퀄라이제이션이라고하며 히스토그램 이퀄라이제이션 튜토리얼에서 논의되었습니다.
대비를 높이기위한 히스토그램 확장에 대해 논의하기 전에 대비를 간략하게 정의하겠습니다.
대조.
대비는 최대 픽셀 강도와 최소 픽셀 강도의 차이입니다.
이 이미지를 고려하십시오.

이 이미지의 히스토그램은 아래와 같습니다.
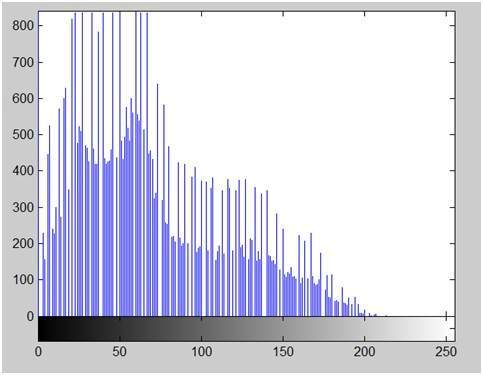
이제이 이미지에서 대비를 계산합니다.
대비 = 225.
이제 이미지의 대비를 높입니다.
이미지의 대비 증가 :
대비를 높이기 위해 이미지의 히스토그램을 늘리는 공식은 다음과 같습니다.
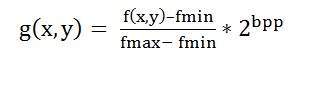
이 공식은 최소 및 최대 픽셀 강도에 회색 수준을 곱해야합니다. 우리의 경우 이미지는 8bpp이므로 회색 수준은 256입니다.
최소값은 0이고 최대 값은 225입니다. 따라서 우리의 경우 공식은 다음과 같습니다.
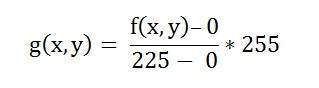
여기서 f (x, y)는 각 픽셀 강도의 값을 나타냅니다. 이미지의 각 f (x, y)에 대해이 공식을 계산합니다.
이렇게하면 대비를 향상시킬 수 있습니다.
히스토그램 스트레칭을 적용하면 다음 이미지가 나타납니다.

이 이미지의 늘어난 히스토그램은 아래와 같습니다.
히스토그램의 모양과 대칭에 유의하십시오. 이제 히스토그램이 늘어나거나 다른 방식으로 확장됩니다. 그것을보세요.
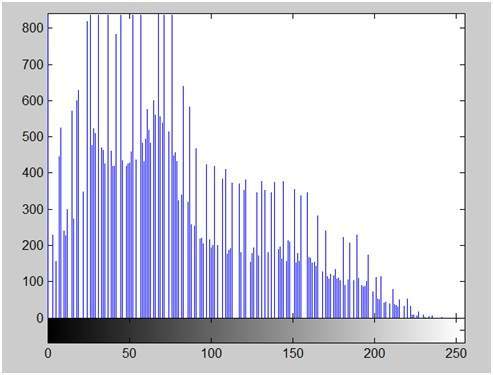
이 경우 이미지의 대비는 다음과 같이 계산할 수 있습니다.
대비 = 240
따라서 이미지의 대비가 증가한다고 말할 수 있습니다.
참고 :이 대비 증가 방법이 항상 작동하는 것은 아니지만 일부 경우에는 실패합니다.
히스토그램 스트레칭 실패
논의했듯이 알고리즘이 일부 경우에 실패합니다. 이러한 경우에는 픽셀 강도가 0이고 이미지에 255가있는 이미지가 포함됩니다.
픽셀 강도 0과 255가 이미지에 존재할 때,이 경우 최소 및 최대 픽셀 강도가되어 이와 같은 공식을 파괴합니다.
원래 공식
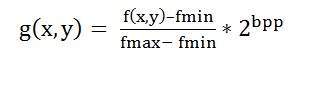
공식에 실패 사례 값 입력 :
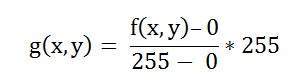
표현을 단순화하면
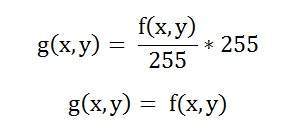
이는 출력 이미지가 처리 된 이미지와 동일 함을 의미합니다. 이는이 이미지에서 히스토그램 확장 효과가 없음을 의미합니다.
PMF와 CDF는 모두 확률과 통계에 속합니다. 이제 당신의 마음 속에 떠오르는 질문은 우리가 확률을 연구하는 이유입니다. PMF와 CDF의이 두 가지 개념이 다음 히스토그램 이퀄라이제이션 튜토리얼에서 사용될 것이기 때문입니다. 따라서 PMF 및 CDF 계산 방법을 모르는 경우 이미지에 히스토그램 이퀄라이제이션을 적용 할 수 없습니다.
PMF는 무엇입니까?
PMF는 확률 질량 함수를 나타냅니다. 이름에서 알 수 있듯이 데이터 세트에있는 각 숫자의 확률을 제공하거나 기본적으로 각 요소의 개수 또는 빈도를 제공한다고 말할 수 있습니다.
PMF 계산 방법 :
PMF는 두 가지 방법으로 계산합니다. 먼저 행렬에서, 다음 튜토리얼에서는 행렬에서 PMF를 계산해야하고 이미지는 2 차원 행렬에 지나지 않습니다.
그런 다음 히스토그램에서 PMF를 계산하는 또 다른 예를 살펴 보겠습니다.
이 매트릭스를 고려하십시오.
| 1 | 2 | 7 | 5 | 6 |
| 7 | 2 | 삼 | 4 | 5 |
| 0 | 1 | 5 | 7 | 삼 |
| 1 | 2 | 5 | 6 | 7 |
| 6 | 1 | 0 | 삼 | 4 |
이제 우리가이 행렬의 PMF를 계산한다면, 여기서 우리는 그것을 어떻게 할 것입니다.
처음에는 행렬의 첫 번째 값을 취한 다음이 값이 전체 행렬에 나타나는 시간을 계산합니다. 카운트 후에는 히스토그램 또는 아래와 같은 표로 나타낼 수 있습니다.
PMF
| 0 | 2 | 2/25 |
| 1 | 4 | 4/25 |
| 2 | 삼 | 3/25 |
| 삼 | 삼 | 3/25 |
| 4 | 2 | 2/25 |
| 5 | 4 | 4/25 |
| 6 | 삼 | 3/25 |
| 7 | 4 | 4/25 |
개수의 합계는 값의 총 개수와 같아야합니다.
히스토그램에서 PMF 계산
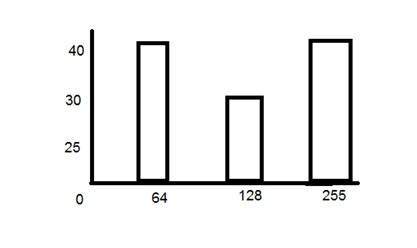
위의 히스토그램은 픽셀 당 8 비트 이미지에 대한 그레이 레벨 값의 주파수를 보여줍니다.
이제 PMF를 계산해야한다면 수직축에서 각 막대의 개수를 간단히 살펴본 다음 총 개수로 나눕니다.
그래서 위 히스토그램의 PMF는 이것입니다.
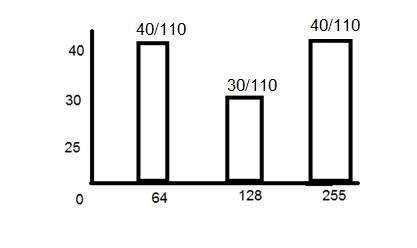
위의 히스토그램에서 주목해야 할 또 다른 중요한 점은 단조 증가하지 않는다는 것입니다. 따라서 단조롭게 증가시키기 위해 CDF를 계산합니다.
CDF 란 무엇입니까?
CDF는 누적 분포 함수를 나타냅니다. PMF에서 계산 한 모든 값의 누적 합계를 계산하는 함수입니다. 기본적으로 이전 값을 합산합니다.
어떻게 계산됩니까?
히스토그램을 사용하여 CDF를 계산합니다. 여기에서 어떻게 이루어집니다. PMF를 보여주는 위에 표시된 히스토그램을 고려하십시오.
이 히스토그램은 단조롭게 증가하지 않으므로 단조롭게 증가합니다.
첫 번째 값을 그대로 유지하고 두 번째 값에 첫 번째 값을 추가하는 식으로 계속됩니다.
위의 PMF 함수의 CDF는 다음과 같습니다.
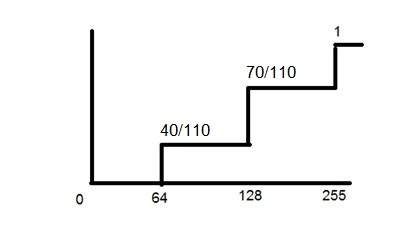
이제 위의 그래프에서 볼 수 있듯이 PMF의 첫 번째 값은 그대로 유지됩니다. PMF의 두 번째 값은 첫 번째 값에 더해져 128 위에 배치됩니다. PMF의 세 번째 값은 CDF의 두 번째 값에 더해져 1과 동일한 110/110이됩니다.
또한 이제 함수는 히스토그램 평준화에 필요한 조건 인 단조롭게 증가하고 있습니다.
히스토그램 이퀄라이제이션에서 PMF 및 CDF 사용
히스토그램 이퀄라이제이션.
히스토그램 이퀄라이제이션은 다음 자습서에서 설명하지만 히스토그램 이퀄라이제이션에 대한 간략한 소개는 아래에 나와 있습니다.
히스토그램 이퀄라이제이션은 이미지의 대비를 향상시키는 데 사용됩니다.
PMF와 CDF는이 자습서의 시작 부분에 설명 된대로 히스토그램 이퀄라이제이션에 모두 사용됩니다. 히스토그램 등화에서 첫 번째와 두 번째 단계는 PMF와 CDF입니다. 히스토그램 이퀄라이제이션에서는 이미지의 모든 픽셀 값을 이퀄라이제이션해야합니다. 따라서 PMF는 이미지에서 각 픽셀 값의 확률을 계산하는 데 도움이됩니다. 그리고 CDF는 이러한 값의 누적 합계를 제공합니다. 더 나아가이 CDF에 레벨을 곱하여 이전 값으로 매핑되는 새로운 픽셀 강도를 찾고 히스토그램이 동일 해집니다.
히스토그램 스트레칭을 사용하여 대비를 높일 수 있음을 이미 확인했습니다. 이 튜토리얼에서는 히스토그램 이퀄라이제이션을 사용하여 대비를 향상시키는 방법을 알아 봅니다.
히스토그램 균등화를 수행하기 전에 히스토그램 균등화에 사용되는 두 가지 중요한 개념을 알아야합니다. 이 두 개념을 PMF 및 CDF라고합니다.
PMF 및 CDF 자습서에서 설명합니다. 히스토그램 이퀄라이제이션의 개념을 성공적으로 파악하려면 방문하십시오.
히스토그램 이퀄라이제이션 :
히스토그램 이퀄라이제이션은 대비를 향상시키는 데 사용됩니다. 콘트라스트가 항상 증가 할 필요는 없습니다. 히스토그램 이퀄라이제이션이 더 나빠질 수있는 경우가있을 수 있습니다. 이 경우 대비가 감소합니다.
아래 이미지를 간단한 이미지로 취하여 히스토그램 이퀄라이제이션을 시작하겠습니다.
영상

이 이미지의 히스토그램 :
이 이미지의 히스토그램은 아래와 같습니다.
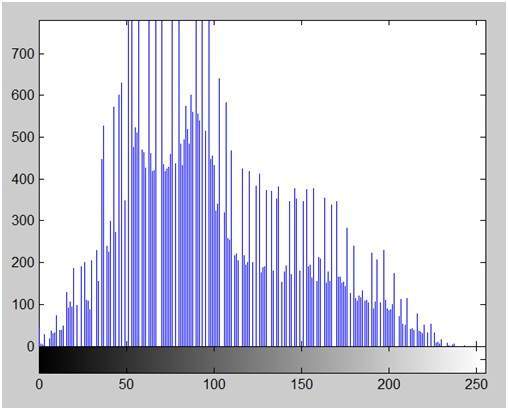
이제 히스토그램 이퀄라이제이션을 수행합니다.
PMF :
먼저이 이미지에있는 모든 픽셀의 PMF (확률 질량 함수)를 계산해야합니다. PMF 계산 방법을 모르는 경우 PMF 계산 자습서를 참조하십시오.
CDF :
다음 단계에는 CDF (누적 분포 함수) 계산이 포함됩니다. CDF 계산 방법을 모르는 경우에도 CDF 계산 자습서를 참조하십시오.
그레이 레벨에 따라 CDF 계산
예를 들어 두 번째 단계에서 계산 된 CDF가 다음과 같다는 것을 고려해 봅시다.
| 그레이 레벨 값 | CDF |
|---|---|
| 0 | 0.11 |
| 1 | 0.22 |
| 2 | 0.55 |
| 삼 | 0.66 |
| 4 | 0.77 |
| 5 | 0.88 |
| 6 | 0.99 |
| 7 | 1 |
그런 다음이 단계에서 CDF 값에 (Gray levels (minus) 1)을 곱합니다.
3bpp 이미지가 있다고 가정합니다. 그러면 우리가 가진 레벨의 수는 8입니다. 그리고 1 빼기 8은 7입니다. 그래서 우리는 CDF에 7을 곱합니다.
| 그레이 레벨 값 | CDF | CDF * (레벨 -1) |
|---|---|---|
| 0 | 0.11 | 0 |
| 1 | 0.22 | 1 |
| 2 | 0.55 | 삼 |
| 삼 | 0.66 | 4 |
| 4 | 0.77 | 5 |
| 5 | 0.88 | 6 |
| 6 | 0.99 | 6 |
| 7 | 1 | 7 |
이제 우리는 새로운 그레이 레벨 값을 픽셀 수로 매핑해야하는 마지막 단계입니다.
이전 그레이 레벨 값에이 픽셀 수가 있다고 가정 해 보겠습니다.
| 그레이 레벨 값 | 회수 |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 삼 | 8 |
| 4 | 10 |
| 5 | 12 |
| 6 | 14 |
| 7 | 16 |
이제 새 값을에 매핑하면 이것이 우리가 얻은 것입니다.
| 그레이 레벨 값 | 새로운 그레이 레벨 값 | 회수 |
|---|---|---|
| 0 | 0 | 2 |
| 1 | 1 | 4 |
| 2 | 삼 | 6 |
| 삼 | 4 | 8 |
| 4 | 5 | 10 |
| 5 | 6 | 12 |
| 6 | 6 | 14 |
| 7 | 7 | 16 |
이제 이러한 새로운 값을 히스토그램에 매핑하면 완료됩니다.
이 기술을 원래 이미지에 적용 해 보겠습니다. 적용 후 다음 이미지와 히스토그램을 얻었습니다.
히스토그램 이퀄라이제이션 이미지

이 이미지의 누적 분포 함수
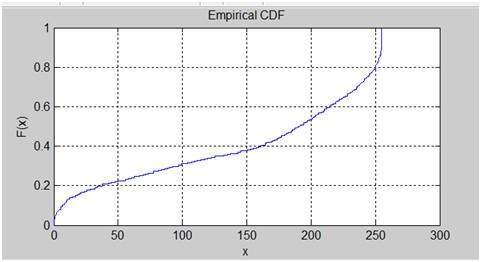
히스토그램 이퀄라이제이션 히스토그램
히스토그램과 이미지 모두 비교

결론
이미지에서 알 수 있듯이 새로운 이미지 대비가 향상되고 히스토그램도 균일화되었음을 알 수 있습니다. 히스토그램 균등화 중에 히스토그램의 전체 모양이 변경되며, 히스토그램 확장에서와 같이 히스토그램의 전체 모양은 동일하게 유지된다는 점에 유의해야합니다.
기본 변환 자습서에서 몇 가지 기본 변환에 대해 논의했습니다. 이 튜토리얼에서는 몇 가지 기본적인 그레이 레벨 변환을 살펴볼 것입니다.
이미지 향상
이미지를 개선하면 비 보강 이미지에 비해 더 나은 대비와 더 자세한 이미지를 제공합니다. 이미지 향상에는 매우 응용 프로그램이 있습니다. 의료 영상, 원격 감지로 캡처 한 영상, 위성 영상 등을 향상시키는 데 사용됩니다.
변환 기능은 다음과 같습니다.
s = T (r)
여기서 r은 입력 이미지의 픽셀이고 s는 출력 이미지의 픽셀입니다. T는 r의 각 값을 s의 각 값에 매핑하는 변환 함수입니다. 이미지 향상은 아래에서 설명하는 그레이 레벨 변환을 통해 수행 할 수 있습니다.
그레이 레벨 변환
세 가지 기본 그레이 레벨 변환이 있습니다.
Linear
Logarithmic
권력 – 법
이러한 전환의 전체 그래프는 아래에 나와 있습니다.
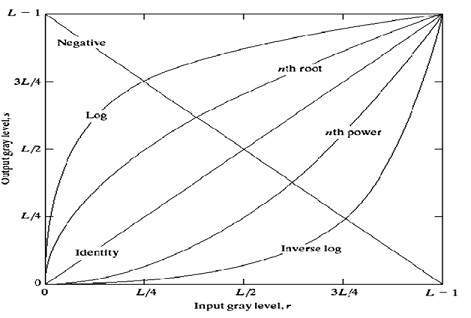
선형 변환
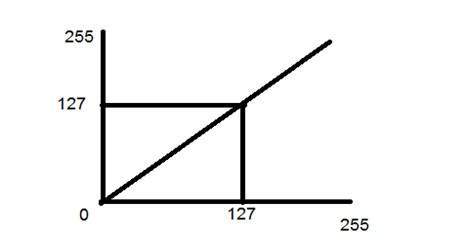
먼저 선형 변환을 살펴 보겠습니다. 선형 변환에는 단순 동일성과 부정 변환이 포함됩니다. 이미지 변환 자습서에서 신원 변환에 대해 설명했지만이 변환에 대한 간략한 설명이 여기에 제공되었습니다.
신원 전환은 직선으로 표시됩니다. 이 전환에서 입력 이미지의 각 값은 출력 이미지의 서로 값에 직접 매핑됩니다. 그 결과 동일한 입력 이미지와 출력 이미지가 생성됩니다. 따라서이를 정체성 변환이라고합니다. 아래에 표시되었습니다
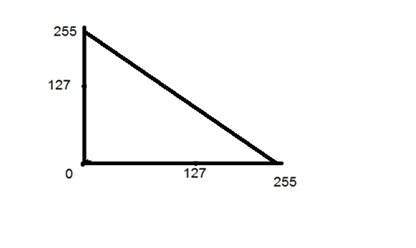
부정적인 변환
두 번째 선형 변환은 음의 변환으로 ID 변환의 반전입니다. 음수 변환에서 입력 이미지의 각 값은 L-1에서 빼고 출력 이미지에 매핑됩니다.
결과는 이와 비슷합니다.
입력 이미지

출력 이미지

이 경우 다음 전환이 수행되었습니다.
s = (L – 1) – r
Einstein의 입력 이미지는 8bpp 이미지이므로이 이미지의 레벨 수는 256입니다. 256을 방정식에 넣으면 다음과 같이됩니다.
s = 255 – r
따라서 각 값은 255로 차감되고 결과 이미지는 위에 표시되었습니다. 따라서, 밝은 픽셀은 어두워지고 어두운 그림은 밝아집니다. 그리고 그것은 이미지 네거티브가됩니다.
아래 그래프에 나와 있습니다.
로그 변환 :
로그 변환에는 두 가지 유형의 변환이 추가로 포함됩니다. 로그 변환 및 역 로그 변환.
Log transformation
The log transformations can be defined by this formula
s = c log(r + 1).
Where s and r are the pixel values of the output and the input image and c is a constant. The value 1 is added to each of the pixel value of the input image because if there is a pixel intensity of 0 in the image, then log (0) is equal to infinity. So 1 is added , to make the minimum value at least 1.
During log transformation , the dark pixels in an image are expanded as compare to the higher pixel values. The higher pixel values are kind of compressed in log transformation. This result in following image enhancement.
The value of c in the log transform adjust the kind of enhancement you are looking for.
입력 이미지

변환 이미지 로그

역 로그 변환은 로그 변환과 반대입니다.
권력 – 법의 변화
또 다른 두 가지 변환은 n 승 및 n 근 변환을 포함하는 멱 법칙 변환입니다. 이러한 변환은 다음 식으로 제공 할 수 있습니다.
s = cr ^ γ
이 기호 γ를 감마라고하며,이 변환을 감마 변환이라고도합니다.
γ 값의 변화는 이미지의 향상에 따라 다릅니다. 서로 다른 디스플레이 장치 / 모니터에는 자체 감마 보정 기능이 있으므로 이미지를 서로 다른 강도로 표시합니다.
이 유형의 변환은 다양한 유형의 디스플레이 장치에 대한 이미지를 향상시키는 데 사용됩니다. 다른 디스플레이 장치의 감마는 다릅니다. 예를 들어 CRT의 감마는 1.8 ~ 2.5 사이에 있으며 이는 CRT에 표시되는 이미지가 어둡다는 것을 의미합니다.
감마 수정.
s = cr ^ γ
s = cr ^ (1 / 2.5)
동일한 이미지이지만 감마 값이 다른 이미지가 여기에 표시되었습니다.
예를 들면 :
감마 = 10

감마 = 8

감마 = 6

이 튜토리얼은 신호 및 시스템의 매우 중요한 개념 중 하나에 관한 것입니다. 우리는 convolution에 대해 완전히 논의 할 것입니다. 뭔데? 왜 그렇습니까? 우리는 그것으로 무엇을 얻을 수 있습니까?
이미지 처리의 기초부터 컨볼 루션에 대해 논의하기 시작합니다.
이미지 처리 란 무엇입니까?
이미지 처리 튜토리얼 소개와 신호 및 시스템에서 논의했듯이 이미지 처리는 이미지가 2 차원 신호일 뿐이므로 신호 및 시스템에 대한 연구입니다.
또한 우리는 이미지 처리에서 입력이 이미지이고 출력이 이미지 인 시스템을 개발하고 있다고 논의했습니다. 이것은 그림으로 표현됩니다.
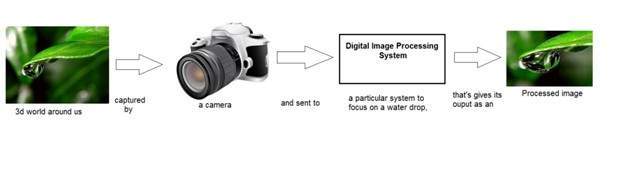
위의 그림에서“디지털 이미지 처리 시스템”이라고 표시된 상자는 블랙 박스로 생각할 수 있습니다.
다음과 같이 더 잘 나타낼 수 있습니다.

지금까지 우리가 어디까지 닿았는지
지금까지 이미지를 조작하는 두 가지 중요한 방법에 대해 논의했습니다. 즉, 블랙 박스는 지금까지 두 가지 방식으로 작동한다고 말할 수 있습니다.
이미지를 조작하는 두 가지 다른 방법은
Graphs (Histograms)

이 방법을 히스토그램 처리라고합니다. 대비 증가, 이미지 향상, 밝기 등에 대한 이전 자습서에서 자세히 논의했습니다.
Transformation functions
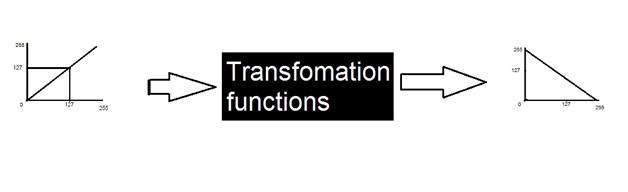
이 방법을 변환이라고하며, 여기서 다양한 유형의 변환과 일부 그레이 레벨 변환을 논의했습니다.
이미지를 다루는 또 다른 방법
여기서 우리는 이미지를 다루는 또 다른 방법을 논의 할 것입니다. 이 다른 방법을 컨볼 루션이라고합니다. 일반적으로 이미지 처리에 사용되는 블랙 박스 (시스템)는 LTI 시스템 또는 선형 시간 불변 시스템입니다. 선형이란 출력이 항상 선형이고 로그도 지수도 아닌 다른 시스템을 의미합니다. 그리고 시간 불변이란 시간 동안 동일하게 유지되는 시스템을 의미합니다.
이제이 세 번째 방법을 사용할 것입니다. 다음과 같이 표현할 수 있습니다.

두 가지 방법으로 수학적으로 표현할 수 있습니다.
g(x,y) = h(x,y) * f(x,y)
"이미지와 컨볼 루션 된 마스크"라고 설명 할 수 있습니다.
또는
g(x,y) = f(x,y) * h(x,y)
이것은“마스크와 결합 된 이미지”라고 설명 할 수 있습니다.
convolution operator (*)가 교환 적이기 때문에 이것을 표현하는 방법은 두 가지가 있습니다. h (x, y)는 마스크 또는 필터입니다.
마스크 란?
마스크도 신호입니다. 2 차원 행렬로 표현할 수 있습니다. 마스크는 보통 1x1, 3x3, 5x5, 7x7 정도입니다. 마스크는 항상 홀수 여야합니다. 그렇지 않으면 마스크의 중간을 찾을 수 없기 때문입니다. 마스크의 중간을 찾아야하는 이유는 무엇입니까? 대답은 아래에 있습니다., 어떻게 컨볼 루션을 수행합니까?
컨볼 루션을 수행하는 방법?
이미지에 컨볼 루션을 수행하려면 다음 단계를 수행해야합니다.
마스크를 수평 및 수직으로 한 번만 뒤집습니다.
마스크를 이미지 위로 슬라이드합니다.
해당 요소를 곱한 다음 추가하십시오.
이미지의 모든 값이 계산 될 때까지이 절차를 반복합니다.
컨볼 루션의 예
컨볼 루션을 수행해 봅시다. 1 단계는 마스크를 뒤집는 것입니다.
마스크:
마스크를 이렇게합시다.
| 1 | 2 | 삼 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
마스크를 수평으로 뒤집기
| 삼 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
마스크를 수직으로 뒤집기
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 삼 | 2 | 1 |
영상:
이미지를 이렇게 생각해 봅시다
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
회선
이미지 위의 컨 볼빙 마스크. 이런 식으로 이루어집니다. 이미지의 각 요소에 마스크 중앙을 배치합니다. 해당 요소를 곱한 다음 추가하고 결과를 마스크 중앙에 배치 한 이미지 요소에 붙여 넣습니다.
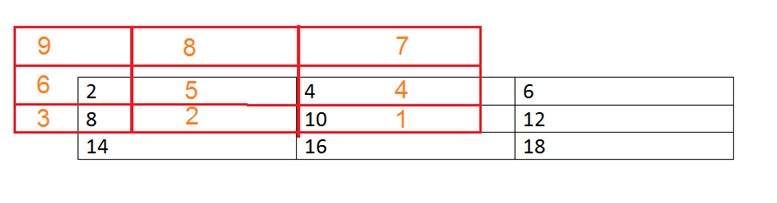
빨간색 상자는 mask이고 주황색 값은 마스크 값입니다. 검은 색 상자와 값은 이미지에 속합니다. 이제 이미지의 첫 번째 픽셀에 대해 값은 다음과 같이 계산됩니다.
첫 번째 픽셀 = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)
= 10 + 16 + 16 + 10
= 52
첫 번째 인덱스의 원본 이미지에 52를 배치하고 이미지의 각 픽셀에 대해이 절차를 반복합니다.
왜 컨볼 루션인가
컨볼 루션은 이전의 두 가지 이미지 조작 방법으로는 달성 할 수없는 것을 얻을 수 있습니다. 여기에는 블러 링, 선명하게하기, 가장자리 감지, 노이즈 감소 등이 포함됩니다.
마스크 란?
마스크는 필터입니다. 마스킹의 개념은 공간 필터링이라고도합니다. 마스킹은 필터링이라고도합니다. 이 개념에서는 이미지에서 직접 수행되는 필터링 작업을 다룹니다.
샘플 마스크는 아래와 같습니다.
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
필터링이란 무엇입니까?
필터링 프로세스는 마스크를 이미지와 컨 볼빙이라고도합니다. 이 프로세스는 컨볼 루션과 동일하므로 필터 마스크는 컨볼 루션 마스크라고도합니다.
수행 방법.
마스크를 필터링하고 적용하는 일반적인 프로세스는 필터 마스크를 이미지의 한 지점에서 지점으로 이동하는 것으로 구성됩니다. 원본 이미지의 각 지점 (x, y)에서 필터의 응답은 미리 정의 된 관계에 의해 계산됩니다. 모든 필터 값은 미리 정의되어 있으며 표준입니다.
필터 유형
일반적으로 두 가지 유형의 필터가 있습니다. 하나는 선형 필터 또는 평활화 필터라고하고 다른 하나는 주파수 도메인 필터라고합니다.
필터가 사용되는 이유는 무엇입니까?
필터는 여러 목적으로 이미지에 적용됩니다. 가장 일반적인 두 가지 용도는 다음과 같습니다.
블러 링 및 노이즈 감소에 필터가 사용됩니다.
필터 사용 또는 가장자리 감지 및 선명도
흐림 및 노이즈 감소 :
필터는 흐림 및 노이즈 감소에 가장 일반적으로 사용됩니다. 블러 링은 큰 물체를 추출하기 전에 이미지에서 작은 세부 사항을 제거하는 것과 같은 사전 처리 단계에서 사용됩니다.
블러 링을위한 마스크.
블러 링의 일반적인 마스크는 다음과 같습니다.
박스 필터
가중 평균 필터
블러 링 과정에서 이미지의 가장자리 내용을 줄이고 서로 다른 픽셀 강도 사이의 전환을 가능한 한 매끄럽게 만듭니다.
흐림의 도움으로 노이즈 감소도 가능합니다.
가장자리 감지 및 선명도 :
마스크 또는 필터를 사용하여 이미지의 가장자리를 감지하고 이미지의 선명도를 높일 수도 있습니다.
가장자리는 무엇입니까?
이미지에서 불연속성의 갑작스런 변화를 가장자리라고 할 수도 있습니다. 이미지의 중요한 전환을 가장자리라고하며 가장자리가있는 그림은 아래와 같습니다.
원본 사진.

가장자리가있는 동일한 그림

블러 링에 대한 간략한 소개는 이전의 마스크 개념 튜토리얼에서 논의되었지만 공식적으로는 여기서 논의 할 것입니다.
블러 링
blur에서는 이미지를 간단히 흐리게 처리합니다. 모든 물체와 그 모양을 정확하게 인식 할 수 있다면 이미지가 더 선명하거나 상세하게 보입니다. 예를 들면. 얼굴이있는 이미지는 눈, 귀, 코, 입술, 이마 등을 매우 선명하게 식별 할 수있을 때 선명 해 보입니다. 이 물체의 모양은 가장자리 때문입니다. 따라서 blur에서는 가장자리 내용을 간단하게 줄이고 한 색상에서 다른 색상으로의 전환을 매우 매끄럽게 만듭니다.
블러 링 vs 확대 / 축소.
이미지를 확대 할 때 흐린 이미지를 보았을 수 있습니다. 픽셀 복제를 사용하여 이미지를 확대 할 때 확대 / 축소 비율이 증가하면 이미지가 흐릿 해집니다. 이 이미지는 또한 디테일이 적지 만 실제 블러 링이 아닙니다.
확대 / 축소에서는 이미지에 새 픽셀을 추가하여 이미지의 전체 픽셀 수를 늘리는 반면 블러 링에서는 일반 이미지와 흐린 이미지의 픽셀 수가 동일하게 유지됩니다.
흐린 이미지의 일반적인 예입니다.

필터 유형.
블러 링은 여러 가지 방법으로 얻을 수 있습니다. 블러 링을 수행하는 데 사용되는 일반적인 필터 유형은 다음과 같습니다.
평균 필터
가중 평균 필터
가우스 필터
이 세 가지 중에서 처음 두 가지에 대해 논의 할 것이며 Gaussian은 다음 자습서에서 나중에 논의 할 것입니다.
평균 필터.
평균 필터는 상자 필터 및 평균 필터라고도합니다. 평균 필터에는 다음과 같은 속성이 있습니다.
이상한 순서 여야합니다.
모든 요소의 합은 1이어야합니다.
모든 요소는 동일해야합니다.
이 규칙을 따르면 3x3 마스크에 대해. 우리는 다음과 같은 결과를 얻습니다.
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
3x3 마스크이므로 9 개의 셀이 있음을 의미합니다. 모든 요소의 합이 1이되어야하는 조건은 각 값을 9로 나누어 얻을 수 있습니다.
1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 = 9/9 = 1
이미지에 3x3 마스크의 결과가 아래에 나와 있습니다.
원본 이미지 :

흐릿한 이미지

결과가 명확하지 않을 수 있습니다. 블러 링을 증가시켜 봅시다. 마스크의 크기를 늘려 블러 링을 늘릴 수 있습니다. 마스크의 크기가 클수록 흐리게 처리됩니다. 마스크가 클수록 더 많은 수의 픽셀이 제공되고 하나의 부드러운 전환이 정의되기 때문입니다.
이미지에 5x5 마스크의 결과가 아래에 나와 있습니다.
원본 이미지 :

흐린 이미지 :

같은 방법으로 mask를 늘리면 블러 링이 더 많아지고 결과는 아래와 같습니다.
이미지에 7x7 마스크의 결과가 아래에 나와 있습니다.
원본 이미지 :

흐린 이미지 :

이미지에 9x9 마스크의 결과는 다음과 같습니다.
원본 이미지 :

흐린 이미지 :

이미지에 11x11 마스크의 결과가 아래에 나와 있습니다.
원본 이미지 :

흐린 이미지 :

가중 평균 필터.
가중 평균 필터에서는 중앙 값에 더 많은 가중치를 부여했습니다. 이로 인해 중심의 기여도가 나머지 값보다 커집니다. 가중 평균 필터링으로 인해 실제로 블러 링을 제어 할 수 있습니다.
가중 평균 필터의 속성은 다음과 같습니다.
이상한 순서 여야합니다.
모든 요소의 합은 1이어야합니다.
중앙 요소의 무게는 다른 모든 요소보다 커야합니다.
필터 1
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 1 | 1 |
(1 및 3) 두 가지 속성이 충족됩니다. 그러나 속성 2는 만족스럽지 않습니다. 따라서이를 만족시키기 위해 전체 필터를 10으로 나누거나 1/10을 곱합니다.
필터 2
| 1 | 1 | 1 |
| 1 | 10 | 1 |
| 1 | 1 | 1 |
분할 계수 = 18.
마스크 소개 튜토리얼에서 가장자리 감지에 대해 간략하게 논의했습니다. 여기서는 공식적으로 에지 감지에 대해 설명합니다.
가장자리는 무엇입니까?
이미지에서 불연속성의 갑작스런 변화를 가장자리라고 할 수도 있습니다. 이미지의 중요한 전환을 가장자리라고합니다.
가장자리 유형.
Geenerally 가장자리에는 세 가지 유형이 있습니다.
수평 가장자리
수직 가장자리
대각선 모서리
가장자리를 감지하는 이유.
이미지의 대부분의 모양 정보는 가장자리로 둘러싸여 있습니다. 따라서 먼저 이미지에서 이러한 가장자리를 감지하고 이러한 필터를 사용한 다음 가장자리가 포함 된 이미지 영역을 향상 시키면 이미지의 선명도가 증가하고 이미지가 더 선명 해집니다.
다음 튜토리얼에서 논의 할 가장자리 감지 용 마스크 중 일부는 다음과 같습니다.
Prewitt 운영자
Sobel 연산자
로빈슨 나침반 마스크
Krisch 나침반 마스크
라플라시안 연산자.
위에서 언급 한 모든 필터는 선형 필터 또는 평활화 필터입니다.
Prewitt 운영자
Prewitt 연산자는 가로 및 세로 가장자리를 감지하는 데 사용됩니다.
Sobel 연산자
소벨 연산자는 Prewitt 연산자와 매우 유사합니다. 또한 파생 마스크이며 가장자리 감지에 사용됩니다. 또한 수평 및 수직 방향의 모서리를 계산합니다.
로빈슨 나침반 마스크
이 연산자는 방향 마스크라고도합니다. 이 연산자에서는 마스크 하나를 가져 와서 각 방향의 모서리를 계산하기 위해 8 개의 나침반 주 방향으로 모두 회전합니다.
Kirsch 나침반 마스크
Kirsch Compass Mask는 가장자리를 찾는 데 사용되는 파생 마스크이기도합니다. Kirsch 마스크는 모든 방향의 모서리를 계산하는데도 사용됩니다.
라플라시안 연산자.
라플라시안 연산자는 또한 이미지에서 가장자리를 찾는 데 사용되는 미분 연산자입니다. Laplacian은 2 차 미분 마스크입니다. 포지티브 라플라시안과 네거티브 라플라시안으로 더 나눌 수 있습니다.
이 모든 마스크는 가장자리를 찾습니다. 일부는 수평 및 수직으로, 일부는 한 방향으로 만 찾고 일부는 모든 방향으로 찾습니다. 이 후 오는 다음 개념은 이미지에서 가장자리를 추출한 후 수행 할 수있는 선명 화입니다.
선명하게하기 :
샤프닝은 블러 링과 반대입니다. 블러 링에서는 가장자리 콘텐츠를 줄이고 sharpneng에서는 가장자리 콘텐츠를 늘립니다. 따라서 이미지의 가장자리 콘텐츠를 늘리려면 먼저 가장자리를 찾아야합니다.
연산자를 사용하여 위에 설명 된 방법 중 하나를 사용하여 모서리를 찾을 수 있습니다. 가장자리를 찾은 후 이미지에 해당 가장자리를 추가하므로 이미지에 더 많은 가장자리가 있고 선명하게 보입니다.
이것은 이미지를 선명하게하는 한 가지 방법입니다.
선명하게하기 이미지는 아래와 같습니다.
원본 이미지

이미지 선명하게

Prewitt 연산자는 이미지의 가장자리 감지에 사용됩니다. 두 가지 유형의 가장자리를 감지합니다.
수평 가장자리
수직 가장자리
가장자리는 이미지의 해당 픽셀 강도 차이를 사용하여 계산됩니다. 가장자리 감지에 사용되는 모든 마스크를 파생 마스크라고도합니다. 이 튜토리얼 시리즈에서 이전에 여러 번 언급했듯이 이미지도 신호이므로 신호의 변화는 미분을 사용해서 만 계산할 수 있기 때문입니다. 그래서 이러한 연산자를 파생 연산자 또는 파생 마스크라고도합니다.
모든 파생 마스크에는 다음 속성이 있어야합니다.
마스크에 반대 기호가 있어야합니다.
마스크의 합은 0과 같아야합니다.
더 많은 무게는 더 많은 가장자리 감지를 의미합니다.
Prewitt 연산자는 수평 방향의 가장자리를 감지하는 마스크와 수직 방향의 가장자리를 감지하는 마스크를 제공합니다.
수직 방향 :
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
위의 마스크는 세로 방향의 가장자리를 찾고 세로 방향의 0 열이기 때문입니다. 이 마스크를 이미지에 컨볼 루션하면 이미지의 수직 가장자리가 제공됩니다.
작동 원리 :
이 마스크를 이미지에 적용하면 수직 가장자리가 두드러집니다. 1 차 도함수처럼 작동하며 가장자리 영역에서 픽셀 강도의 차이를 계산합니다. 가운데 열이 0이므로 이미지의 원래 값을 포함하지 않고 해당 가장자리 주변의 오른쪽 및 왼쪽 픽셀 값의 차이를 계산합니다. 이것은 가장자리 강도를 증가시키고 원본 이미지에 비해 상대적으로 향상됩니다.
수평 방향 :
| -1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
위의 마스크는 가로 방향으로 가장자리를 찾고 0 열이 가로 방향이기 때문입니다. 이 마스크를 이미지에 컨볼 루션하면 이미지에서 수평 가장자리가 두드러집니다.
작동 원리 :
이 마스크는 이미지의 수평 가장자리를 두드러지게합니다. 또한 위 마스크의 원리에 따라 작동하며 특정 가장자리의 픽셀 강도 간의 차이를 계산합니다. 마스크의 중앙 행은 0으로 구성되어 있으므로 이미지에있는 가장자리의 원래 값을 포함하지 않고 특정 가장자리의 위와 아래 픽셀 강도의 차이를 계산합니다. 따라서 강도의 갑작스런 변화를 증가시키고 가장자리를 더 잘 보이게 만듭니다. 위의 두 마스크는 모두 파생 마스크의 원리를 따릅니다. 두 마스크 모두 반대 부호가 있으며 두 마스크 합계는 0입니다. 위의 두 마스크가 모두 표준화되어 있으며 값을 변경할 수 없기 때문에 세 번째 조건은이 연산자에 적용되지 않습니다.
이제 이러한 마스크가 작동하는 것을 볼 시간입니다.
샘플 이미지 :
다음은 위의 두 마스크를 한 번에 하나씩 적용 할 샘플 사진입니다.

수직 마스크 적용 후 :
위의 샘플 이미지에 세로 마스크를 적용하면 다음과 같은 이미지를 얻을 수 있습니다. 이 이미지에는 세로 가장자리가 포함되어 있습니다. 가로 가장자리 그림과 비교하면 더 정확하게 판단 할 수 있습니다.

수평 마스크 적용 후 :
위의 샘플 이미지에 수평 마스크를 적용하면 다음과 같은 이미지를 얻을 수 있습니다.

비교:
보시다시피 수직 마스크를 적용한 첫 번째 그림에서 모든 수직 가장자리가 원본 이미지보다 더 잘 보입니다. 마찬가지로 두 번째 그림에서 수평 마스크를 적용했으며 결과적으로 모든 수평 가장자리가 표시됩니다. 따라서 이러한 방식으로 이미지에서 수평 및 수직 가장자리를 모두 감지 할 수 있음을 알 수 있습니다.
소벨 연산자는 Prewitt 연산자와 매우 유사합니다. 또한 파생 마스크이며 가장자리 감지에 사용됩니다. Prewitt 연산자와 마찬가지로 sobel 연산자는 이미지에서 두 종류의 가장자리를 감지하는데도 사용됩니다.
수직 방향
수평 방향
Prewitt 통신사와의 차이점 :
가장 큰 차이점은 소벨 연산자에서는 마스크 계수가 고정되어 있지 않으며 파생 마스크의 속성을 위반하지 않는 한 우리의 요구 사항에 따라 조정할 수 있다는 것입니다.
다음은 Sobel 연산자의 수직 마스크입니다.
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
이 마스크는 Prewitt 연산자 수직 마스크와 정확히 동일하게 작동합니다. 단 하나의 차이점은 첫 번째와 세 번째 열의 중앙에 "2"와 "-2"값이 있다는 것입니다. 이미지에 적용 할 때이 마스크는 수직 가장자리를 강조합니다.
작동 원리 :
이 마스크를 이미지에 적용하면 수직 가장자리가 두드러집니다. 1 차 도함수처럼 작동하며 가장자리 영역에서 픽셀 강도의 차이를 계산합니다.
가운데 열이 0이므로 이미지의 원래 값을 포함하지 않고 해당 가장자리 주변의 오른쪽 및 왼쪽 픽셀 값의 차이를 계산합니다. 또한 첫 번째와 세 번째 열의 중심 값은 각각 2와 -2입니다.
이것은 가장자리 영역 주변의 픽셀 값에 더 많은 가중치를 부여합니다. 이것은 가장자리 강도를 증가시키고 원본 이미지에 비해 상대적으로 향상됩니다.
다음은 Sobel 연산자의 수평 마스크입니다.
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
위의 마스크는 가로 방향으로 가장자리를 찾고 0 열이 가로 방향이기 때문입니다. 이 마스크를 이미지에 컨볼 루션하면 이미지에서 수평 가장자리가 두드러집니다. 유일한 차이점은 첫 번째와 세 번째 행의 중심 요소로 2와 -2가 있다는 것입니다.
작동 원리 :
이 마스크는 이미지의 수평 가장자리를 두드러지게합니다. 또한 위 마스크의 원리에 따라 작동하며 특정 가장자리의 픽셀 강도 간의 차이를 계산합니다. 마스크의 중앙 행은 0으로 구성되어 있으므로 이미지에있는 가장자리의 원래 값을 포함하지 않고 특정 가장자리의 위와 아래 픽셀 강도의 차이를 계산합니다. 따라서 강도의 갑작스런 변화를 증가시키고 가장자리를 더 잘 보이게 만듭니다.
이제 이러한 마스크가 작동하는 것을 볼 시간입니다.
샘플 이미지 :
다음은 위의 두 마스크를 한 번에 하나씩 적용 할 샘플 사진입니다.

수직 마스크 적용 후 :
위의 샘플 이미지에 세로 마스크를 적용하면 다음과 같은 이미지를 얻을 수 있습니다.

수평 마스크 적용 후 :
위의 샘플 이미지에 가로 마스크를 적용하면 다음 이미지를 얻을 수 있습니다.

비교:
보시다시피 수직 마스크를 적용한 첫 번째 그림에서 모든 수직 가장자리가 원본 이미지보다 더 잘 보입니다. 마찬가지로 두 번째 그림에서 수평 마스크를 적용했으며 결과적으로 모든 수평 가장자리가 표시됩니다.
따라서 이러한 방식으로 이미지에서 수평 및 수직 가장자리를 모두 감지 할 수 있음을 알 수 있습니다. 또한 소벨 연산자와 Prewitt 연산자의 결과를 비교하면 소벨 연산자가 Prewitt 연산자에 비해 더 많은 모서리를 찾거나 모서리를 더 잘 보이게 만드는 것을 알 수 있습니다.
이는 소벨 연산자에서 가장자리 주변의 픽셀 강도에 더 많은 가중치를 할당했기 때문입니다.
마스크에 더 많은 가중치 적용
이제 마스크에 더 많은 가중치를 적용하면 더 많은 가장자리를 얻을 수 있음을 알 수 있습니다. 또한 튜토리얼의 시작 부분에서 언급했듯이 소벨 연산자에는 고정 계수가 없으므로 여기에 또 다른 가중치 연산자가 있습니다.
| -1 | 0 | 1 |
| -5 | 0 | 5 |
| -1 | 0 | 1 |
이 마스크의 결과를 Prewitt 수직 마스크와 비교할 수 있다면 마스크에 더 많은 가중치를 할당했기 때문에이 마스크가 Prewitt에 비해 더 많은 가장자리를 제공한다는 것이 분명합니다.
Robinson 나침반 마스크는 가장자리 감지에 사용되는 또 다른 유형의 파생 마스크입니다. 이 연산자는 방향 마스크라고도합니다. 이 연산자에서 우리는 마스크 하나를 가져와 다음과 같은 8 개 나침반 주요 방향으로 모두 회전합니다.
North
북서
West
남서부
South
남동부
East
북동쪽
고정 마스크가 없습니다. 아무 마스크 나 사용할 수 있으며 위에서 언급 한 모든 방향에서 가장자리를 찾기 위해 회전해야합니다. 모든 마스크는 0 열의 방향을 기준으로 회전합니다.
예를 들어 북쪽 방향에있는 다음 마스크를보고 회전하여 모든 방향 마스크를 만듭니다.
북쪽 방향 마스크
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
북서 방향 마스크
| 0 | 1 | 2 |
| -1 | 0 | 1 |
| -2 | -1 | 0 |
웨스트 디렉션 마스크
| 1 | 2 | 1 |
| 0 | 0 | 0 |
| -1 | -2 | -1 |
남서 방향 마스크
| 2 | 1 | 0 |
| 1 | 0 | -1 |
| 0 | -1 | -2 |
남쪽 방향 마스크
| 1 | 0 | -1 |
| 2 | 0 | -2 |
| 1 | 0 | -1 |
남동 방향 마스크
| 0 | -1 | -2 |
| 1 | 0 | -1 |
| 2 | 1 | 0 |
동쪽 방향 마스크
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
북동 방향 마스크
| -2 | -1 | 0 |
| -1 | 0 | 1 |
| 0 | 1 | 2 |
보시다시피 모든 방향은 0 방향을 기준으로합니다. 각 마스크는 방향의 가장자리를 제공합니다. 이제 위의 전체 마스크의 결과를 보겠습니다. 모든 모서리를 찾아야하는 샘플 사진이 있다고 가정 해 보겠습니다. 다음은 샘플 사진입니다.
샘플 사진 :

이제이 이미지에 위의 모든 필터를 적용하고 다음과 같은 결과를 얻습니다.
북쪽 방향 모서리

북서 방향 모서리

서쪽 방향 모서리

남서쪽 방향 모서리

남쪽 방향 모서리

남동 방향 모서리

동쪽 방향 모서리

북동쪽 방향 모서리

위의 모든 마스크를 적용하면 모든 방향으로 가장자리가 생깁니다. 결과는 이미지에 따라 다릅니다. 북동쪽 가장자리가없는 이미지가 있다고 가정하면 해당 마스크가 효과가 없습니다.
Kirsch Compass Mask는 가장자리를 찾는 데 사용되는 파생 마스크이기도합니다. 이것은 로빈슨 나침반이 나침반의 모든 8 개 방향에서 모서리를 찾는 것과 같습니다. Robinson과 kirsch 나침반 마스크의 유일한 차이점은 Kirsch에는 표준 마스크가 있지만 Kirsch에서는 자체 요구 사항에 따라 마스크를 변경한다는 것입니다.
Kirsch Compass Masks의 도움으로 우리는 다음 8 가지 방향에서 가장자리를 찾을 수 있습니다.
North
북서
West
남서부
South
남동부
East
북동쪽
파생 마스크의 모든 속성을 따르는 표준 마스크를 가져온 다음 회전하여 가장자리를 찾습니다.
예를 들어 북쪽 방향에있는 다음 마스크를보고 회전하여 모든 방향 마스크를 만듭니다.
북쪽 방향 마스크
| -삼 | -삼 | 5 |
| -삼 | 0 | 5 |
| -삼 | -삼 | 5 |
북서 방향 마스크
| -삼 | 5 | 5 |
| -삼 | 0 | 5 |
| -삼 | -삼 | -삼 |
웨스트 디렉션 마스크
| 5 | 5 | 5 |
| -삼 | 0 | -삼 |
| -삼 | -삼 | -삼 |
남서 방향 마스크
| 5 | 5 | -삼 |
| 5 | 0 | -삼 |
| -삼 | -삼 | -삼 |
남쪽 방향 마스크
| 5 | -삼 | -삼 |
| 5 | 0 | -삼 |
| 5 | -삼 | -삼 |
남동 방향 마스크
| -삼 | -삼 | -삼 |
| 5 | 0 | -삼 |
| 5 | 5 | -삼 |
동쪽 방향 마스크
| -삼 | -삼 | -삼 |
| -삼 | 0 | -삼 |
| 5 | 5 | 5 |
북동 방향 마스크
| -삼 | -삼 | -삼 |
| -삼 | 0 | 5 |
| -삼 | 5 | 5 |
보시다시피 모든 방향이 덮여 있고 각 마스크는 자체 방향의 가장자리를 제공합니다. 이제 이러한 마스크의 개념을 더 잘 이해할 수 있도록 실제 이미지에 적용합니다. 모든 모서리를 찾아야하는 샘플 사진이 있다고 가정 해 보겠습니다. 다음은 샘플 사진입니다.
샘플 사진

이제이 이미지에 위의 모든 필터를 적용하고 다음과 같은 결과를 얻습니다.
북쪽 방향 모서리

북서 방향 모서리

서쪽 방향 모서리

남서쪽 방향 모서리

남쪽 방향 모서리

남동 방향 모서리

동쪽 방향 모서리

북동쪽 방향 모서리

위의 모든 마스크를 적용하면 모든 방향으로 가장자리가 생깁니다. 결과는 이미지에 따라 다릅니다. 북동쪽 가장자리가없는 이미지가 있다고 가정하면 해당 마스크가 효과가 없습니다.
라플라시안 연산자는 또한 이미지에서 가장자리를 찾는 데 사용되는 미분 연산자입니다. Laplacian과 Prewitt, Sobel, Robinson 및 Kirsch와 같은 다른 연산자의 주요 차이점은 모두 1 차 미분 마스크이지만 Laplacian은 2 차 미분 마스크라는 것입니다. 이 마스크에는 두 개의 추가 분류가 있는데 하나는 Positive Laplacian Operator이고 다른 하나는 Negative Laplacian Operator입니다.
Laplacian과 다른 연산자의 또 다른 차이점은 다른 연산자와 달리 Laplacian은 특정 방향으로 가장자리를 제거하지 않았지만 다음 분류에서 가장자리를 제거한다는 것입니다.
안쪽 가장자리
바깥 쪽 가장자리
Laplacian 연산자의 작동 방식을 살펴 보겠습니다.
긍정적 인 라플라시안 연산자 :
Positive Laplacian에는 마스크의 중앙 요소가 음수이고 마스크의 모서리 요소가 0이어야하는 표준 마스크가 있습니다.
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
양수 라플라시안 연산자는 이미지에서 바깥 쪽 가장자리를 꺼내는 데 사용됩니다.
네거티브 라플라시안 연산자 :
음수 라플라시안 연산자에는 중앙 요소가 양수 여야하는 표준 마스크도 있습니다. 모서리의 모든 요소는 0이어야하며 마스크의 나머지 요소는 -1이어야합니다.
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
Negative Laplacian 연산자는 이미지의 안쪽 가장자리를 제거하는 데 사용됩니다.
작동 원리 :
Laplacian은 파생 연산자입니다. 그것의 사용은 이미지에서 그레이 레벨 불연속성을 강조하고 천천히 변화하는 그레이 레벨로 영역을 강조하려고합니다. 결과적으로이 작업을 수행하면 어두운 배경에 회색 가장자리 선과 기타 불연속성이있는 이미지가 생성됩니다. 이것은 이미지의 안쪽과 바깥 쪽 가장자리를 생성합니다.
중요한 것은 이러한 필터를 이미지에 적용하는 방법입니다. 동일한 이미지에 양수 및 음수 라플라시안 연산자를 모두 적용 할 수는 없습니다. 하나만 적용해야하지만 기억해야 할 점은 이미지에 양의 Laplacian 연산자를 적용하면 원본 이미지에서 결과 이미지를 빼서 선명한 이미지를 얻는다는 것입니다. 마찬가지로 네거티브 Laplacian 연산자를 적용하면 결과 이미지를 원본 이미지에 추가하여 선명한 이미지를 얻어야합니다.
이 필터를 이미지에 적용하고 이미지에서 안쪽과 바깥 쪽 가장자리를 어떻게 얻을 수 있는지 살펴 보겠습니다. 다음 샘플 이미지가 있다고 가정합니다.
샘플 이미지

After applying Positive Laplacian Operator:
긍정적 인 라플라시안 연산자를 적용하면 다음 이미지를 얻을 수 있습니다.

After applying Negative Laplacian Operator:
음수 Laplacian 연산자를 적용하면 다음 이미지가 표시됩니다.

우리는 많은 영역에서 이미지를 다루었습니다. 이제 우리는 주파수 영역에서 신호 (이미지)를 처리하고 있습니다. 이 푸리에 급수 및 주파수 영역은 순전히 수학이므로 수학의 일부를 최소화하고 DIP에서의 사용에 더 집중하려고 노력할 것입니다.
주파수 영역 분석
지금까지 우리가 신호를 분석 한 모든 영역을 시간과 관련하여 분석합니다. 그러나 주파수 영역에서 우리는 시간과 관련하여 신호를 분석하지 않고 주파수와 관련하여 분석합니다.
공간 영역과 주파수 영역의 차이.
공간 영역에서 우리는 이미지를있는 그대로 다룹니다. 이미지의 픽셀 값은 장면에 따라 변경됩니다. 주파수 영역에서는 픽셀 값이 공간 영역에서 변하는 속도를 다룹니다.
간단하게하기 위해 이렇게합시다.
Spatial domain

단순 공간 영역에서는 이미지 매트릭스를 직접 처리합니다. 주파수 영역에서는 이와 같은 이미지를 처리합니다.
주파수 영역
먼저 이미지를 주파수 분포로 변환합니다. 그런 다음 블랙 박스 시스템은 수행해야하는 모든 처리를 수행하며이 경우 블랙 박스의 출력은 이미지가 아니라 변환입니다. 역변환을 수행 한 후 이미지로 변환되어 공간 영역에서 볼 수 있습니다.
그림으로 볼 수 있습니다.
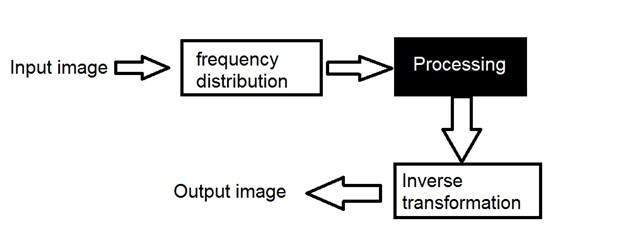
여기서는 변형이라는 단어를 사용했습니다. 그것은 실제로 무엇을 의미합니까?
변환.
신호는 변환이라고하는 수학적 연산자를 사용하여 시간 도메인에서 주파수 도메인으로 변환 될 수 있습니다. 이를 수행하는 많은 종류의 변형이 있습니다. 그들 중 일부는 아래에 나와 있습니다.
푸리에 시리즈
푸리에 변환
라플라스 변환
Z 변환
이 모든 것 중에서 우리는 다음 튜토리얼에서 푸리에 급수와 푸리에 변환을 철저히 논의 할 것입니다.
주파수 성분
공간 영역의 모든 이미지는 주파수 영역으로 표현 될 수 있습니다. 그러나이 주파수는 실제로 무엇을 의미합니까?
주파수 성분을 두 가지 주요 성분으로 나눌 것입니다.
High frequency components
고주파 성분은 이미지의 가장자리에 해당합니다.
Low frequency components
이미지의 저주파 성분은 부드러운 영역에 해당합니다.
주파수 영역 분석의 마지막 자습서에서 신호를 주파수 영역으로 변환하는 데 푸리에 시리즈와 푸리에 변환이 사용된다는 점에 대해 논의했습니다.
Fourier
푸리에는 1822 년 수학자였습니다. 그는 신호를 주파수 영역으로 변환하기 위해 푸리에 급수와 푸리에 변환을 제공합니다.
Fourier Series
푸리에 급수는 단순히 특정 가중치를 곱하면 주기적 신호를 사인과 코사인의 합으로 나타낼 수 있으며 주기적 신호를 다음과 같은 특성을 가진 추가 신호로 나눌 수 있음을 나타냅니다.
신호는 사인과 코사인입니다.
신호는 서로의 고조파입니다.
그림으로 볼 수 있습니다.
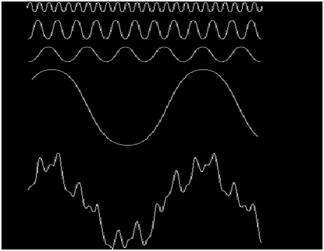
위의 신호에서 마지막 신호는 실제로 위의 모든 신호의 합입니다. 이것이 푸리에의 아이디어였습니다.
계산 방법.
주파수 영역에서 보았 듯이 주파수 영역에서 이미지를 처리하려면 먼저 사용하여 주파수 영역으로 변환해야하고 출력의 역을 가져와 다시 공간 영역으로 변환해야합니다. 이것이 푸리에 급수와 푸리에 변환에 두 가지 공식이있는 이유입니다. 하나는 변환 용이고 다른 하나는 다시 공간 영역으로 변환합니다.
푸리에 급수
푸리에 급수는이 공식으로 나타낼 수 있습니다.
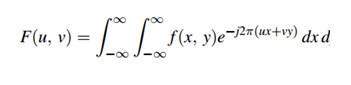
역수는이 공식으로 계산할 수 있습니다.
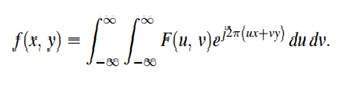
푸리에 변환
푸리에 변환은 곡선 아래의 면적이 유한 한 비주기 신호도 특정 가중치를 곱한 후 사인과 코사인의 적분으로 나타낼 수 있음을 나타냅니다.
푸리에 변환에는 이미지 압축 (예 : JPEG 압축), 필터링 및 이미지 분석을 포함하는 다양한 응용 프로그램이 있습니다.
푸리에 급수와 변환의 차이점
푸리에 급수와 푸리에 변환은 모두 푸리에로 주어 지지만 그 차이점은주기 신호에는 푸리에 급수가 적용되고 비주기 신호에는 푸리에 변환이 적용된다는 것입니다.
어느 것이 이미지에 적용되는지.
이제 질문은 이미지, 푸리에 시리즈 또는 푸리에 변환에 적용되는 것입니다. 글쎄,이 질문에 대한 답은 이미지가 무엇인지에 있습니다. 이미지는 비 주기적입니다. 그리고 이미지가 주기적이지 않기 때문에 푸리에 변환을 사용하여 이미지를 주파수 영역으로 변환합니다.
이산 푸리에 변환.
우리는 이미지와 사실 디지털 이미지를 다루고 있으므로 디지털 이미지의 경우 이산 푸리에 변환 작업을 할 것입니다.

정현파의 위 푸리에 항을 고려하십시오. 여기에는 세 가지가 포함됩니다.
공간 주파수
Magnitude
Phase
공간 주파수는 이미지의 밝기와 직접적인 관련이 있습니다. 정현파의 크기는 대비와 직접 관련이 있습니다. 대비는 최대 픽셀 강도와 최소 픽셀 강도의 차이입니다. 단계에는 색상 정보가 포함됩니다.
2 차원 이산 푸리에 변환의 공식은 다음과 같습니다.
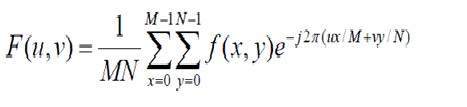
이산 푸리에 변환은 실제로 샘플링 된 푸리에 변환이므로 이미지를 나타내는 일부 샘플을 포함합니다. 위의 공식에서 f (x, y)는 이미지를 나타내고 F (u, v)는 이산 푸리에 변환을 나타냅니다. 2 차원 역 이산 푸리에 변환의 공식은 다음과 같습니다.
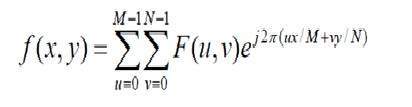
역 이산 푸리에 변환은 푸리에 변환을 다시 이미지로 변환합니다.
이 신호를 고려하십시오.
이제 우리는 FFT 크기 스펙트럼을 계산 한 다음 이동 된 FFT 크기 스펙트럼을 계산할 이미지를 볼 수 있습니다. 그런 다음 이동 된 스펙트럼의 로그를 가져옵니다.
원본 이미지

푸리에 변환 크기 스펙트럼

이동 푸리에 변환

이동 된 크기 스펙트럼

지난 튜토리얼에서 주파수 영역의 이미지에 대해 논의했습니다. 이 튜토리얼에서는 주파수 영역과 이미지 (공간 영역) 간의 관계를 정의합니다.
예를 들면 :
이 예를 고려하십시오.

주파수 영역에서 동일한 이미지를 다음과 같이 표현할 수 있습니다.

이제 이미지 또는 공간 영역과 주파수 영역 사이의 관계는 무엇입니까? 이 관계는 Convolution 정리라고하는 정리로 설명 할 수 있습니다.
컨볼 루션 정리
공간 영역과 주파수 영역 사이의 관계는 컨볼 루션 정리에 의해 설정 될 수 있습니다.
컨볼 루션 정리는 다음과 같이 나타낼 수 있습니다.
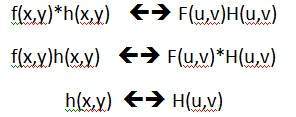
공간 영역의 컨볼 루션은 주파수 영역의 필터링과 같고 그 반대의 경우도 마찬가지입니다.
주파수 도메인의 필터링은 다음과 같이 나타낼 수 있습니다.

The steps in filtering are given below.
첫 번째 단계에서는 공간 영역에서 이미지를 사전 처리해야합니다. 이는 대비 또는 밝기를 증가시키는 것을 의미합니다.
그런 다음 이미지의 이산 푸리에 변환을 수행합니다.
그런 다음 이산 푸리에 변환을 중앙에 배치합니다. 이산 푸리에 변환을 모서리에서 중앙으로 가져옵니다.
그런 다음 필터링을 적용합니다. 즉, 푸리에 변환에 필터 함수를 곱합니다.
그런 다음 다시 DFT를 중앙에서 모서리로 이동합니다.
마지막 단계는 역 이산 푸리에 변환을 수행하여 결과를 주파수 영역에서 공간 영역으로 되 돌리는 것입니다.
이 사후 처리 단계는 이미지의 모양을 높이는 사전 처리와 마찬가지로 선택 사항입니다.
필터
주파수 영역의 필터 개념은 컨볼 루션의 마스크 개념과 동일합니다.
이미지를 주파수 영역으로 변환 한 후 필터링 과정에서 일부 필터를 적용하여 이미지에 대해 다른 종류의 처리를 수행합니다. 처리에는 이미지 흐림, 이미지 선명 화 등이 포함됩니다.
이러한 목적을위한 일반적인 필터 유형은 다음과 같습니다.
이상적인 고역 통과 필터
이상적인 저역 통과 필터
가우스 고역 통과 필터
가우스 저역 통과 필터
다음 자습서에서는 필터에 대해 자세히 설명합니다.
지난 튜토리얼에서는 필터에 대해 간략하게 설명합니다. 이 튜토리얼에서는 이에 대해 철저히 논의 할 것입니다. 논의하기 전에 먼저 마스크에 대해 이야기합시다. 마스크의 개념은 컨볼 루션 및 마스크 튜토리얼에서 논의되었습니다.
블러 링 마스크 대 파생 마스크.
블러 링 마스크와 파생 마스크를 비교해 보겠습니다.
블러 링 마스크 :
블러 링 마스크에는 다음과 같은 속성이 있습니다.
블러 링 마스크의 모든 값은 양수입니다.
모든 값의 합은 1과 같습니다.
블러 링 마스크를 사용하여 가장자리 내용을 줄입니다.
마스크의 크기가 커질수록 더 스무딩 효과가 나타납니다.
파생 마스크 :
파생 마스크에는 다음과 같은 속성이 있습니다.
파생 마스크에는 양수 값과 음수 값이 있습니다.
미분 마스크의 모든 값의 합은 0입니다.
파생 마스크에 의해 가장자리 콘텐츠가 증가합니다.
마스크의 크기가 커질수록 더 많은 가장자리 내용이 증가합니다.
블러 링 마스크와 고역 통과 필터 및 저역 통과 필터가있는 파생 마스크 간의 관계.
블러 링 마스크와 고역 통과 필터와 저역 통과 필터가있는 파생 마스크의 관계는 간단하게 정의 할 수 있습니다.
블러 링 마스크는 로우 패스 필터라고도합니다.
파생 마스크는 고역 통과 필터라고도합니다.
고역 통과 주파수 구성 요소 및 저역 통과 주파수 구성 요소
고역 통과 주파수 성분은 에지를 나타내는 반면 저역 통과 주파수 성분은 부드러운 영역을 나타냅니다.
이상적인 저역 통과 및 이상적인 고역 통과 필터
이것은 저역 통과 필터의 일반적인 예입니다.
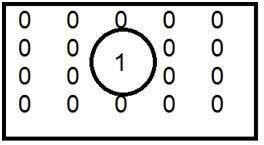
하나는 내부에 배치하고 0은 외부에 배치하면 이미지가 흐려집니다. 이제 크기를 1로 늘리면 블러 링이 증가하고 가장자리 내용이 감소합니다.
이것은 고역 통과 필터의 일반적인 예입니다.
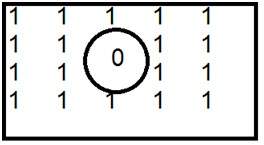
0이 내부에 배치되면 가장자리가 생성되어 스케치 된 이미지를 제공합니다. 주파수 영역에서 이상적인 저역 통과 필터는 다음과 같습니다.

이상적인 저역 통과 필터는 다음과 같이 그래픽으로 나타낼 수 있습니다.
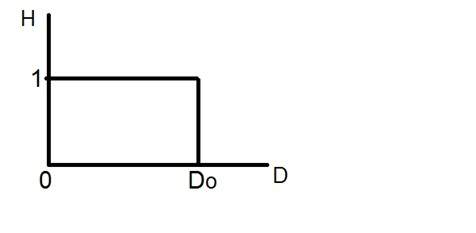
이제이 필터를 실제 이미지에 적용하고 얻은 결과를 살펴 보겠습니다.
샘플 이미지.

주파수 영역의 이미지

이 이미지에 필터 적용

결과 이미지

같은 방법으로 이상적인 하이 패스 필터를 이미지에 적용 할 수 있습니다. 그러나 분명히 결과는 다를 것입니다. 저역 통과는 에지 콘텐츠를 줄이고 고역 통과는 그것을 증가시킵니다.
가우시안 로우 패스 및 가우스 하이 패스 필터
가우스 저역 통과 및 가우스 고역 통과 필터는 이상적인 저역 통과 및 고역 통과 필터에서 발생하는 문제를 최소화합니다.
이 문제를 벨소리 효과라고합니다. 이것은 어떤 지점에서 한 색상 사이의 전환을 정확하게 정의 할 수 없기 때문에 그 지점에서 링 효과가 나타나기 때문입니다.
이 그래프를보세요.
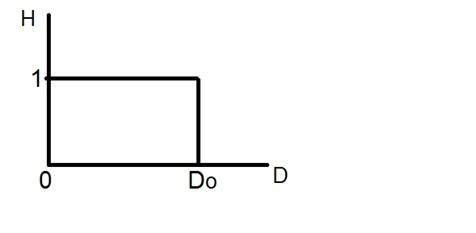
이것은 이상적인 저역 통과 필터의 표현입니다. 이제 Do의 정확한 지점에서 값이 0 또는 1이라는 것을 알 수 없습니다.이 지점에서 벨소리 효과가 나타납니다.
따라서 이상적인 저역 통과 및 이상적인 고역 통과 필터로 나타나는 효과를 줄이기 위해 다음과 같은 가우시안 저역 통과 필터와 가우스 고역 통과 필터가 도입되었습니다.
가우스 저역 통과 필터
필터링과 저역 통과의 개념은 동일하게 유지되지만 전환 만 달라지고 더 부드러워집니다.
가우스 저역 통과 필터는 다음과 같이 나타낼 수 있습니다.

부드러운 곡선 전환으로 인해 각 지점에서 Do 값을 정확하게 정의 할 수 있습니다.
가우스 고역 통과 필터
Gaussian 고역 통과 필터는 이상적인 고역 통과 필터와 동일한 개념을 가지고 있지만 전환은 이상적인 고역 통과 필터에 비해 더 부드럽습니다.
이 튜토리얼에서는 색 공간에 대해 이야기 할 것입니다.
색 공간이란 무엇입니까?
색 공간은 다양한 목적으로 이미지 처리 및 신호 및 시스템에 사용되는 다양한 유형의 색상 모드입니다. 일반적인 색상 공간 중 일부는 다음과 같습니다.
RGB
CMY’K
Y’UV
YIQ
Y’CbCr
HSV
RGB
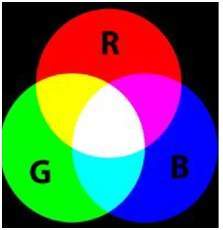
RGB는 가장 널리 사용되는 색 공간이며 이전 튜토리얼에서 이미 논의했습니다. RGB는 빨간색 녹색과 파란색을 나타냅니다.
RGB 모델에 따르면 각 색상 이미지는 실제로 세 가지 다른 이미지로 구성됩니다. 빨간색 이미지, 파란색 이미지 및 검은 색 이미지입니다. 일반 회색조 이미지는 하나의 행렬로만 정의 할 수 있지만 실제로 컬러 이미지는 세 개의 다른 행렬로 구성됩니다.
하나의 컬러 이미지 매트릭스 = 빨간색 매트릭스 + 파란색 매트릭스 + 녹색 매트릭스
이것은 아래의이 예에서 가장 잘 볼 수 있습니다.
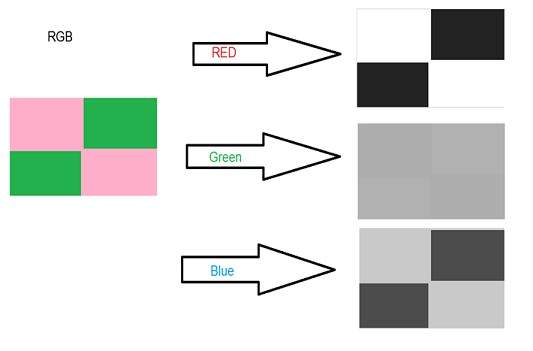
RGB의 응용
RGB 모델의 일반적인 응용 프로그램은 다음과 같습니다.
음극선 관 (CRT)
액정 디스플레이 (LCD)
플라즈마 디스플레이 또는 TV와 같은 LED 디스플레이
컴퓨팅 모니터 또는 대규모 화면
CMYK

RGB에서 CMY로 변환
RGB에서 CMY 로의 변환은이 방법을 사용하여 수행됩니다.
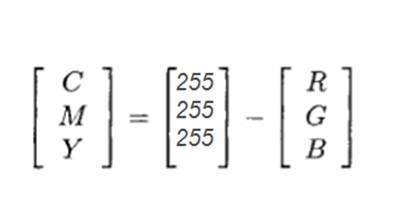
컬러 이미지가 있다고 가정하면 RED, GREEN 및 BLUE의 세 가지 배열이 있음을 의미합니다. 이제 CMY로 변환하려면 다음을 수행해야합니다. 최대 레벨 수만큼 빼야합니다. 1입니다. 각 매트릭스는 빼고 각각의 CMY 매트릭스는 결과로 채워집니다.
Y'UV
Y'UV는 하나의 루마 (Y ')와 두 개의 색차 (UV) 구성 요소로 색 공간을 정의합니다. Y'UV 컬러 모델은 다음 합성 컬러 비디오 표준에서 사용됩니다.
NTSC (National Television System Committee)
PAL (Phase Alternating Line)
SECAM (Sequential couleur a amemoire, French for "sequential color with memory)

Y'CbCr
Y'CbCr 색상 모델은 Y '를 포함하고, 루마 성분 및 cb 및 cr은 청색 차이 및 적색 차이 크로마 성분입니다.
절대 색 공간이 아닙니다. 주로 디지털 시스템에 사용됩니다.
일반적인 응용 프로그램에는 JPEG 및 MPEG 압축이 포함됩니다.
Y'UV는 종종 Y'CbCr의 용어로 사용되지만 완전히 다른 형식입니다. 이 둘의 주요 차이점은 전자는 아날로그이고 후자는 디지털이라는 것입니다.

마지막 이미지 압축 튜토리얼에서는 압축에 사용되는 몇 가지 기술에 대해 설명합니다.
일부 데이터는 결국 손실이므로 손실 압축 인 JPEG 압축에 대해 논의 할 것입니다.
먼저 이미지 압축이 무엇인지 살펴 보겠습니다.
이미지 압축
이미지 압축은 디지털 이미지에서 데이터를 압축하는 방법입니다.
이미지 압축의 주요 목적은 다음과 같습니다.
효율적인 형태로 데이터 저장
효율적인 형태로 데이터 전송
이미지 압축은 손실이 있거나 손실이 없을 수 있습니다.
JPEG 압축
JPEG는 공동 사진 전문가 그룹을 의미합니다. 이미지 압축에있어 최초의 국제 표준입니다. 오늘날 널리 사용됩니다. 손실이있을뿐만 아니라 손실이 없을 수도 있습니다. 하지만 오늘 여기서 논의 할 기술은 손실 압축 기술입니다.
jpeg 압축 작동 방식 :
첫 번째 단계는 이미지를 각각 8 x8 크기의 블록으로 나누는 것입니다.

이 8x8 이미지에 다음 값이 포함되어 있다고 가정 해 보겠습니다.
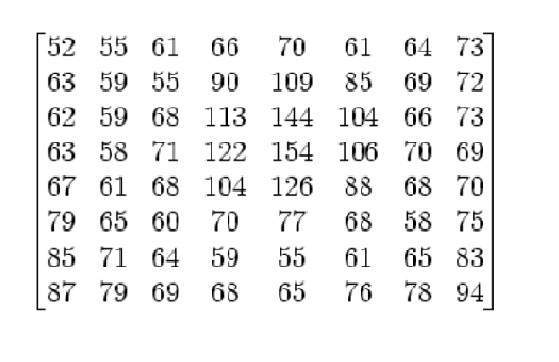
이제 픽셀 강도의 범위는 0에서 255까지입니다. 범위를 -128에서 127로 변경합니다.
각 픽셀 값에서 128을 빼면 -128에서 127까지의 픽셀 값이됩니다. 각 픽셀 값에서 128을 빼면 다음과 같은 결과가 나옵니다.

이제이 공식을 사용하여 계산합니다.
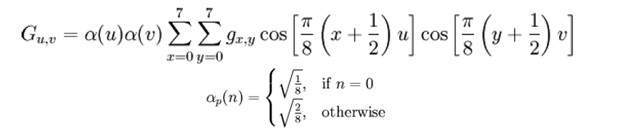
결과는 A (j, k) 행렬에 저장됩니다.
JPEG 압축을 계산하는 데 사용되는 표준 매트릭스가 있으며, 이는 휘도 매트릭스라고하는 매트릭스로 제공됩니다.
이 매트릭스는 아래와 같습니다.
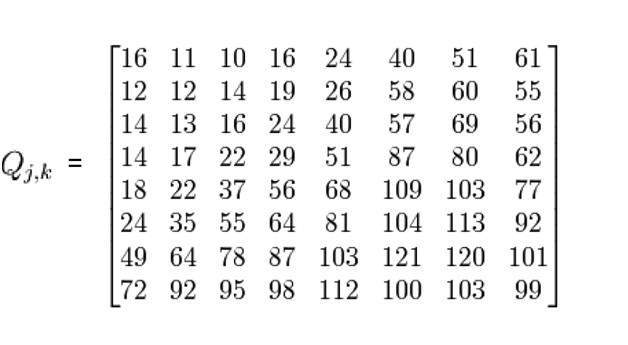
다음 공식 적용

우리는 신청 후이 결과를 얻었습니다.

이제 우리는 ZIG-ZAG 운동 인 JPEG 압축에서 수행되는 실제 트릭을 수행합니다. 위 매트릭스의 지그재그 시퀀스는 아래와 같습니다. 앞에있는 모든 0을 찾을 때까지 지그재그를 수행해야합니다. 따라서 이제 이미지가 압축됩니다.

Summarizing JPEG compression
첫 번째 단계는 이미지를 Y'CbCr로 변환하고 Y '채널을 선택하고 8 x 8 블록으로 나누는 것입니다. 그런 다음 첫 번째 블록에서 시작하여 범위를 -128에서 127까지 매핑합니다. 그 후에 행렬의 이산 푸리에 변환을 찾아야합니다. 그 결과는 양자화되어야합니다. 마지막 단계는 zig zag 방식으로 인코딩을 적용하고 모두 0을 찾을 때까지 수행하는 것입니다.
이 1 차원 배열을 저장하면 완료됩니다.
Note. You have to repeat this procedure for all the block of 8 x 8.
광학 문자 인식은 일반적으로 OCR로 축약됩니다. 여기에는 손으로 쓰고 타이핑 한 텍스트의 스캔 이미지를 기계 텍스트로 기계 및 전기적으로 변환하는 작업이 포함됩니다. 인쇄 된 텍스트를 전자적으로 검색하고, 더 간결하게 저장하고, 온라인에 표시하고, 기계 번역, 텍스트 음성 변환 및 텍스트 마이닝과 같은 기계 프로세스에 사용할 수 있도록 인쇄 된 텍스트를 디지털화하는 일반적인 방법입니다.
최근에는 OCR (Optical Character Recognition) 기술이 산업 전반에 적용되어 문서 관리 프로세스에 혁명을 일으켰습니다. OCR은 스캔 한 문서를 단순한 이미지 파일 이상으로 만들어 컴퓨터가 인식하는 텍스트 콘텐츠가 포함 된 완전히 검색 가능한 문서로 변모했습니다. OCR의 도움으로 사람들은 더 이상 중요한 문서를 전자 데이터베이스에 입력 할 때 수동으로 다시 입력 할 필요가 없습니다. 대신 OCR은 관련 정보를 추출하여 자동으로 입력합니다. 그 결과 더 적은 시간에 정확하고 효율적인 정보 처리가 가능합니다.
광학 문자 인식에는 여러 연구 분야가 있지만 가장 일반적인 분야는 다음과 같습니다.
Banking:
OCR의 용도는 분야에 따라 다릅니다. 널리 알려진 애플리케이션 중 하나는 은행 업무로, OCR은 사람의 개입없이 수표를 처리하는 데 사용됩니다. 수표를 기계에 삽입 할 수 있으며, 그 위에 기록 된 내용이 즉시 스캔되며 정확한 금액이 이체됩니다. 이 기술은 인쇄 된 수표에 거의 완벽하게 적용되었으며 손으로 쓴 수표에도 상당히 정확하지만 때때로 수동 확인이 필요합니다. 전반적으로 이것은 많은 은행에서 대기 시간을 줄입니다.
Blind and visually impaired persons:
OCR이면의 연구 시작에서 주요 요인 중 하나는 과학자가 시각 장애인에게 책을 큰 소리로 읽을 수있는 컴퓨터 나 장치를 만들고 싶어한다는 것입니다. 이 연구 과학자는 우리에게 가장 일반적으로 문서 스캐너로 알려진 평판 스캐너를 만들었습니다.
Legal department:
법률 산업에서도 종이 문서를 디지털화하려는 중요한 움직임이있었습니다. 공간을 절약하고 종이 파일 상자를 살펴볼 필요가 없도록 문서를 스캔하고 컴퓨터 데이터베이스에 입력합니다. OCR은 문서를 텍스트로 검색 할 수 있도록 만들어 프로세스를 더욱 단순화하여 데이터베이스에서 한 번 더 쉽게 찾고 작업 할 수 있도록합니다. 법률 전문가는 이제 전자 형식의 방대한 문서 라이브러리에 빠르고 쉽게 액세스 할 수 있으며 몇 가지 키워드를 입력하기 만하면 찾을 수 있습니다.
Retail Industry:
바코드 인식 기술은 OCR 과도 관련이 있습니다. 우리는 일상적인 사용에서이 기술의 사용을 봅니다.
Other Uses:
OCR은 교육, 금융 및 정부 기관을 포함한 다른 많은 분야에서 널리 사용됩니다. OCR은 온라인에서 수많은 텍스트를 제공하여 학생들의 비용을 절약하고 지식을 공유 할 수 있도록합니다. 인보이스 이미징 애플리케이션은 재무 기록을 추적하고 지불 백 로그가 쌓이는 것을 방지하기 위해 많은 비즈니스에서 사용됩니다. 정부 기관 및 독립 조직에서 OCR은 다른 프로세스 중에서도 데이터 수집 및 분석을 단순화합니다. 기술이 계속 발전함에 따라 필기 인식 사용 증가를 포함하여 OCR 기술에 대한 응용 프로그램이 점점 더 많이 발견되고 있습니다.
컴퓨터 시각 인식
컴퓨터 비전은 컴퓨터 소프트웨어와 하드웨어를 사용하여 인간의 비전을 모델링하고 복제하는 것과 관련이 있습니다. 공식적으로 컴퓨터 비전을 정의하면 컴퓨터 비전은 장면에 존재하는 구조의 속성 측면에서 2D 이미지에서 3D 장면을 재구성, 중단 및 이해하는 방법을 연구하는 학문이라는 것입니다.
휴먼 비전 시스템의 작동을 이해하고 활성화하기 위해서는 다음 분야의 지식이 필요합니다.
컴퓨터 과학
전기 공학
Mathematics
Physiology
Biology
인지 과학
컴퓨터 비전 계층 :
컴퓨터 비전은 다음과 같은 세 가지 기본 범주로 나뉩니다.
저수준 비전 : 특징 추출을위한 프로세스 이미지를 포함합니다.
중급 비전 : 물체 인식 및 3D 장면 해석 포함
높은 수준의 비전 : 활동, 의도 및 행동과 같은 장면에 대한 개념 설명이 포함됩니다.
관련 분야 :
Computer Vision은 다음 분야와 크게 겹칩니다.
이미지 처리 : 이미지 조작에 중점을 둡니다.
패턴 인식 : 패턴을 분류하기 위해 다양한 기술을 연구합니다.
사진 측량 : 이미지에서 정확한 측정 값을 얻는 것과 관련이 있습니다.
컴퓨터 비전 대 이미지 처리 :
이미지 처리는 이미지에서 이미지로의 변환을 연구합니다. 이미지 처리의 입력과 출력은 모두 이미지입니다.
컴퓨터 비전은 이미지에서 물리적 객체에 대한 명시적이고 의미있는 설명을 구성하는 것입니다. 컴퓨터 비전의 출력은 3D 장면의 구조에 대한 설명 또는 해석입니다.
애플리케이션 예 :
Robotics
Medicine
Security
Transportation
공업 자동화
로봇 공학 응용 :
현지화로 로봇 위치를 자동으로 결정
Navigation
장애물 회피
조립 (페그 인 홀, 용접, 도장)
조작 (예 : PUMA 로봇 조작기)
HRI (Human Robot Interaction) : 사람들과 상호 작용하고 서비스를 제공하는 지능형 로봇
의학 신청 :
분류 및 검출 (예 : 병변 또는 세포 분류 및 종양 검출)
2D / 3D 분할
3D 인간 장기 재건 (MRI 또는 초음파)
비전 유도 로봇 수술
산업 자동화 응용 :
산업 검사 (결함 감지)
Assembly
바코드 및 포장 라벨 판독
개체 정렬
문서 이해 (예 : OCR)
보안 응용 프로그램 :
생체 인식 (홍채, 지문, 얼굴 인식)
특정 의심스러운 활동 또는 행동을 감시 감지
교통 신청 :
자율 주행 차
안전 (예 : 운전자 경계 모니터링)
컴퓨터 그래픽
컴퓨터 그래픽은 컴퓨터를 사용하여 만든 그래픽과 특수한 그래픽 하드웨어 및 소프트웨어의 도움을 받아 컴퓨터가 이미지 데이터를 표현한 것입니다. 공식적으로 우리는 컴퓨터 그래픽이 기하학적 객체 (모델링)와 그 이미지 (렌더링)의 생성, 조작 및 저장이라고 말할 수 있습니다.
컴퓨터 그래픽 하드웨어의 출현과 함께 개발 된 컴퓨터 그래픽 분야. 오늘날 컴퓨터 그래픽은 거의 모든 분야에서 사용됩니다. 데이터를 시각화하기 위해 많은 강력한 도구가 개발되었습니다. 컴퓨터 그래픽 분야는 회사가 비디오 게임에서 사용하기 시작했을 때 더욱 인기를 얻었습니다. 오늘날 그것은 수십억 달러 규모의 산업이며 컴퓨터 그래픽 개발의 주요 원동력입니다. 몇 가지 일반적인 응용 분야는 다음과 같습니다.
CAD (Computer Aided Design)
프리젠 테이션 그래픽
3d 애니메이션
교육과 훈련
그래픽 사용자 인터페이스
컴퓨터 지원 설계 :
건물, 자동차, 항공기 및 기타 여러 제품의 설계에 사용
가상 현실 시스템을 만드는 데 사용합니다.
프리젠 테이션 그래픽 :
일반적으로 재무, 통계 데이터를 요약하는 데 사용됩니다.
슬라이드 생성에 사용
3d 애니메이션 :
Pixar, DresmsWorks와 같은 회사에서 영화 산업에서 많이 사용
게임과 영화에 특수 효과를 추가합니다.
교육과 훈련:
컴퓨터 생성 물리적 시스템 모델
의료 시각화
3D MRI
치과 및 뼈 스캔
조종사 훈련 용 자극기 등
그래픽 사용자 인터페이스 :
버튼, 아이콘 및 기타 구성 요소와 같은 그래픽 사용자 인터페이스 개체를 만드는 데 사용됩니다.