이미지 변환
논의하기 전에 이미지 변환이 무엇인지, 변환이 무엇인지 논의 할 것입니다.
변환
변환은 기능입니다. 일부 작업을 수행 한 후 한 세트를 다른 세트로 매핑하는 기능입니다.
디지털 이미지 처리 시스템
우리는 이미 입문 튜토리얼에서 디지털 이미지 처리에서 입력이 이미지이고 출력이 이미지가되는 시스템을 개발할 것임을 이미 보았습니다. 그리고 시스템은 입력 이미지에 대해 일부 처리를 수행하고 처리 된 이미지로 출력을 제공합니다. 아래와 같습니다.
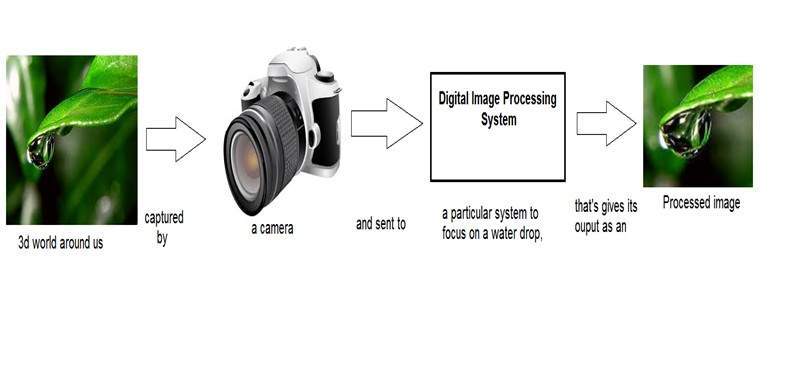
이제이 디지털 시스템 내부에 적용된 이미지를 처리하여 출력으로 변환하는 기능을 변환 기능이라고 할 수 있습니다.
변환 또는 관계를 보여 주므로 image1이 image2로 변환되는 방식입니다.
이미지 변환.
이 방정식을 고려하십시오
G (x, y) = T {f (x, y)}
이 방정식에서
F (x, y) = 변환 함수를 적용해야하는 입력 이미지.
G (x, y) = 출력 이미지 또는 처리 된 이미지.
T는 변환 함수입니다.
입력 이미지와 처리 된 출력 이미지 간의 이러한 관계는 다음과 같이 나타낼 수도 있습니다.
s = T (r)
여기서 r은 실제로 모든 지점에서 f (x, y)의 픽셀 값 또는 그레이 레벨 강도입니다. 그리고 s는 어느 지점에서나 g (x, y)의 픽셀 값 또는 그레이 레벨 강도입니다.
기본 그레이 레벨 변환은 기본 그레이 레벨 변환 튜토리얼에서 논의되었습니다.
이제 우리는 매우 기본적인 변환 함수에 대해 논의 할 것입니다.
예
이 변환 함수를 고려하십시오.
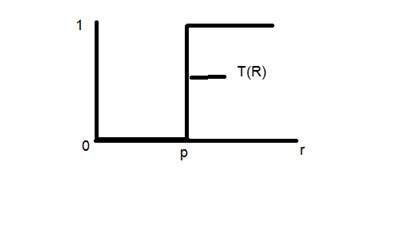
포인트 r을 256으로, 포인트 p를 127로 설정합니다.이 이미지를 1bpp 이미지로 간주합니다. 즉, 0과 1 인 두 수준의 강도 만 있습니다. 따라서이 경우 그래프에 표시된 변환은 다음과 같이 설명 될 수 있습니다.
127 (포인트 p) 미만의 모든 픽셀 강도 값은 0이며 검은 색을 의미합니다. 그리고 127보다 큰 모든 픽셀 강도 값은 1입니다. 즉, 흰색을 의미합니다. 하지만 정확한 127 점에서 갑작스런 전송 변화가있어서 정확한 지점에서 값이 0 또는 1이 될 것이라고 말할 수 없습니다.
수학적으로이 변환 함수는 다음과 같이 표시 될 수 있습니다.
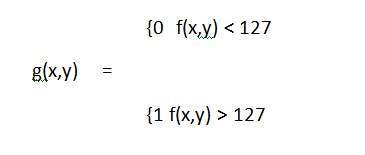
이와 같은 또 다른 변형을 고려하십시오.
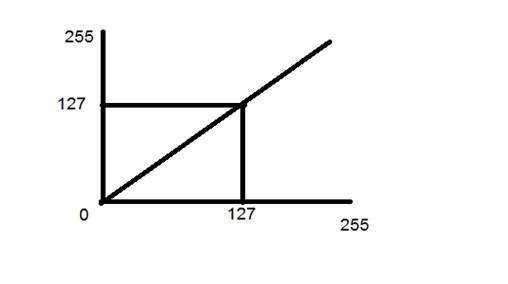
이제이 특정 그래프를 보면 입력 이미지와 출력 이미지 사이에 직선 전환 선이 표시됩니다.
각 픽셀 또는 입력 이미지의 강도 값에 대해 출력 이미지의 강도 값이 동일 함을 보여줍니다. 즉, 출력 이미지는 입력 이미지의 정확한 복제본입니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
g (x, y) = f (x, y)
이 경우 입력 및 출력 이미지는 아래와 같습니다.
