주파수 영역 소개

우리는 많은 영역에서 이미지를 다루었습니다. 이제 우리는 주파수 영역에서 신호 (이미지)를 처리하고 있습니다. 이 푸리에 급수 및 주파수 영역은 순전히 수학이므로 수학의 일부를 최소화하고 DIP에서의 사용에 더 초점을 맞추려고 노력할 것입니다.

주파수 영역 분석

지금까지 우리가 신호를 분석 한 모든 영역을 시간과 관련하여 분석합니다. 그러나 주파수 영역에서 우리는 시간과 관련하여 신호를 분석하지 않고 주파수와 관련하여 분석합니다.

공간 영역에서는 이미지를있는 그대로 다룹니다. 이미지의 픽셀 값은 장면에 따라 변경됩니다. 주파수 영역에서는 픽셀 값이 공간 영역에서 변경되는 속도를 다룹니다.

간단하게하기 위해 이렇게합시다.

단순 공간 영역에서는 이미지 매트릭스를 직접 처리합니다. 주파수 영역에서는 이와 같은 이미지를 처리합니다.

먼저 이미지를 주파수 분포로 변환합니다. 그런 다음 블랙 박스 시스템은 수행해야하는 모든 처리를 수행하고이 경우 블랙 박스의 출력은 이미지가 아니라 변형입니다. 역변환을 수행 한 후 이미지로 변환하여 공간 영역에서 볼 수 있습니다.

그림으로 볼 수 있습니다.

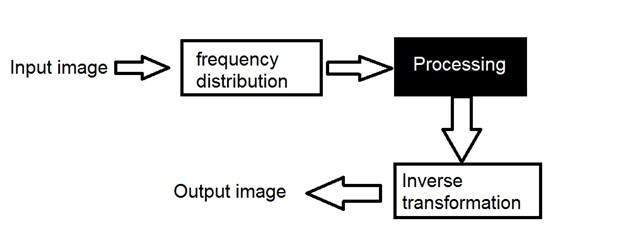
여기서는 변형이라는 단어를 사용했습니다. 그것은 실제로 무엇을 의미합니까?

신호는 변환이라고하는 수학적 연산자를 사용하여 시간 도메인에서 주파수 도메인으로 변환 될 수 있습니다. 이를 수행하는 많은 종류의 변형이 있습니다. 그들 중 일부는 아래에 나와 있습니다.

이 모든 것 중에서 우리는 다음 튜토리얼에서 푸리에 급수와 푸리에 변환을 철저히 논의 할 것입니다.

공간 영역의 모든 이미지는 주파수 영역으로 표현 될 수 있습니다. 그러나이 주파수는 실제로 무엇을 의미합니까?

주파수 성분을 두 가지 주요 성분으로 나눌 것입니다.

고주파 성분은 이미지의 가장자리에 해당합니다.

이미지의 저주파 성분은 부드러운 영역에 해당합니다.