Modelowanie dzielenia liczby całkowitej na ułamek
Tutaj, w tej lekcji, nauczymy się, jak używać modelu pola do dzielenia liczby całkowitej przez ułamek. Istnieje liczba całkowita i ułamek, który dzieli tę liczbę. Traktujemy liczbę całkowitą jako tyle kwadratów, ile wskazuje liczba. Dzielimy każdy z kwadratów na tyle części, na ile wskazuje mianownik ułamka. Wynik tego podziału znajdujemy, zliczając całkowitą liczbę części kwadratów.
Example:
Podzielić 3 ÷ $ \ frac {1} {2} $ za pomocą modelu obszaru.
Solution
Step 1:
Cała liczba 3 jest traktowana jako trzy kwadraty. Ponieważ ułamek jest równy połowie, każdy z kwadratów jest podzielony na dwie połowy.
Step 2:
Teraz policzono połówki wszystkich trzech kwadratów i okazało się, że jest to 6. Oto odpowiedź, którą otrzymujemy dzieląc 3 przez $ \ frac {1} {2} $ .
A więc 3 ÷ $ \ frac {1} {2} $ = 6
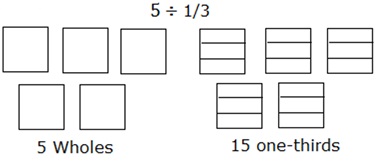
Podziel 5 ÷ $ \ frac {1} {3} $ za pomocą modelu obszaru.
Rozwiązanie
Step 1:
Podzielenie 5 na jedną trzecią można modelować w następujący sposób:
Rozważ 5 kwadratów jako 5 całości. Każdy z kwadratów jest dalej podzielony na trzy części lub jedną trzecią.
Step 2:
Wtedy zliczenie całkowitej liczby takich części kwadratów lub całości daje odpowiedź, która wynosi 15.
Czyli 5 ÷ $ \ frac {1} {3} $ = 15
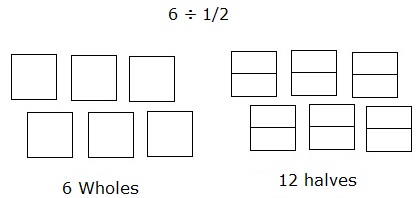
Podzielić 6 ÷ $ \ frac {1} {2} $ za pomocą modelu obszaru.
Rozwiązanie
Step 1:
Podział 6 na połówki można modelować w następujący sposób:
Rozważ 6 kwadratów jako 6 całości. Każdy z kwadratów jest dalej podzielony na dwie części lub połówki.
Step 2:
Wtedy zliczenie całkowitej liczby takich części kwadratów lub całości daje odpowiedź, która wynosi 12.
A więc 6 ÷ $ \ frac {1} {2} $ = 12