Высота и расстояние - решенные примеры

Q 1 - С точки 375 метров от подножия башни, вершина башни видна под углом 45 °, тогда высота (в метрах) башни равна?

А - 375

В - 450

С - 225

Д - 250

Answer - A

Explanation

From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

Q 2 - Угол подъема башни в точке 90 м от нее составляет кровать ^-1 (4/5), тогда высота башни равна

А - 45

В - 90

С - 112,5

Д - 150

Answer - C

Explanation

Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

Q 3 - На ровной поверхности угол подъема вершины башни составляет 30 °. При приближении на 20 метров угол подъема составляет 45 °. Тогда высота башни равна

А - 10

В - √3

С - 10√3

Д - 20√3

Answer - C

Explanation

Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

Q 4 - Углы поднятия вершин двух вертикальных башен, если смотреть из средней точки линий, соединяющих подножия башен, составляют 45 ° и 60 °. Отношение высоты башен составляет

А - √3: 2

В - √3: 1

С - 2: √3

Д - 2: 1

Answer - B

Explanation

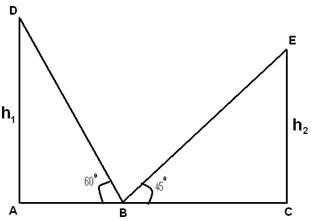
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

Q 5 - Высота двух башен 90 метров и 45 метров. Линия, соединяющая их вершины, составляет угол 450 с горизонталью, тогда расстояние между двумя башнями равно

А - 22,5 м

B - 45 м

C - 60 м

D - 30 м

Answer - B

Explanation

Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

Q 6 - Из точки P на ровной поверхности угол подъема верхней башни составляет 60 °. Если высота башни составляет 180 м, расстояние от точки P до подножия башни равно

А - 60√3

В - 40√3

С - 30√3

Д - 20√3

Answer - A

Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

Q 7 - Вершина башни высотой 25 метров составляет угол подъема 450 с основанием электрического столба и угол подъема 30 градусов с вершиной столба. Найдите высоту электрического столба.

А - 25√3

В - 25 ((√3-1) / √3)

С - 25 / √3

D - 25 ((1-√3) / √3)

Answer - B

Explanation

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

Q 8 - Наблюдатель ростом 1,4 м находится на расстоянии 10√3 от башни. Угол подъема от его глаза до вершины башни составляет 60 °. Высота башни составляет

A - 12,4 м

B - 6,2 м

С - 11,4√3 м

D - 11,4 м

Answer - D

Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

Q 9 - Мужчина смотрит с вершины башни на лодку, несущуюся от башни. Лодка на расстоянии 75 метров от вышки делает угол снижения в 60 ° взглядом человека. Через 10 секунд угол наклона становится 45 °. Какова приблизительная скорость лодки, если предположить, что она движется в стоячей воде?

А - 54 км / ч

B - 64 км / ч

C - 24 км / ч

D - 19,8 км / ч

Answer - D

Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

Q 10 - Расстояние по горизонтали между двумя башнями составляет 90 м. Угловое понижение верха первого, если смотреть сверху второго, высота которого составляет 180 м, составляет 450 м. Тогда высота первого составляет

А - 90√3 м

B - 45 м

C - 90 м

D - 150 м

Answer - C

Explanation