Analog İletişim - Hızlı Kılavuz

İletişim kelimesi, "paylaşmak" anlamına gelen Latince commūnicāre kelimesinden gelir. İletişim, bilgi alışverişi için temel adımdır.

Örneğin beşikteki bir bebek annesine ihtiyaç duyduğunda ağlayarak iletişim kurar. Bir inek tehlike altındayken yüksek sesle molar. Bir kişi bir dil yardımıyla iletişim kurar. İletişim, paylaşılacak köprüdür.

Communication iki veya daha fazla birey arasında kelimeler, eylemler, işaretler vb. yollarla bilgi alışverişi süreci olarak tanımlanabilir.

Bir İletişim Sisteminin Parçaları

İletişim sağlayan herhangi bir sistem aşağıdaki şekilde gösterildiği gibi üç önemli ve temel bölümden oluşur.

• Sendermesaj gönderen kişidir. Sinyalin iletildiği bir verici istasyon olabilir.

• Channel hedefe ulaşmak için mesaj sinyallerinin geçtiği ortamdır.

• Receivermesajı alan kişidir. İletilen sinyalin alındığı bir alıcı istasyon olabilir.

Sinyal Türleri

Bir bilgiyi jestler, sesler, eylemler vb. Gibi bazı yollarla iletmek şu şekilde adlandırılabilir: signaling. Dolayısıyla, bir sinyal bazı bilgileri ileten bir enerji kaynağı olabilir. Bu sinyal, gönderen ve alıcı arasında bir iletişim kurulmasına yardımcı olur.

Bir mesajı iletmek için bir mesafe kat eden bir elektriksel dürtü veya bir elektromanyetik dalga, signal iletişim sistemlerinde.

Karakteristiklerine bağlı olarak, sinyaller esas olarak iki tipte sınıflandırılır: Analog ve Dijital. Analog ve Dijital sinyaller, aşağıdaki şekilde gösterildiği gibi ayrıca sınıflandırılır.

Analog Sinyal

Zamanla değişen bir miktarı temsil eden sürekli, zamanla değişen bir sinyal, Analog Signal. Bu sinyal, kendisini temsil eden miktarın anlık değerlerine göre zamana göre değişmeye devam eder.

Misal

100 litre kapasiteli bir depoyu saatte (06.00-07.00) dolduran bir musluğu düşünelim. Depoyu doldurma kısmı, değişen zamana göre değişir. Bu, 15 dakika sonra (6:15), tankın dörtte bir kısmı dolarken, sabah 6: 45'te, tankın 3 / 4'ü dolar.

Depodaki değişen zamana göre değişen su kısımlarını grafiğe dökmeye çalışırsak aşağıdaki şekle benzeyecektir.

Bu görselde gösterilen sonuç zamana göre değiştiği (arttığı) için bu time varying quantityAnalog miktar olarak anlaşılabilir. Şekilde eğimli bir çizgi ile bu durumu temsil eden sinyal,Analog Signal. Analog sinyaller ve analog değerlere dayalı iletişime,Analog Communication.

Dijital sinyal

Doğası gereği ayrık olan veya biçim olarak sürekli olmayan bir sinyal, bir sinyal olarak adlandırılabilir. Digital signal. Bu sinyalin, sanki belirli bir anda türetilmiş gibi, önceki değerlere dayanmayan ayrı ayrı gösterilen ayrı değerleri vardır.

Misal

20 öğrencisi olan bir sınıf düşünelim. Bir hafta içindeki katılımları planlanırsa aşağıdaki şekle benzeyecektir.

Bu şekilde değerler ayrı olarak belirtilmiştir. Örneğin Çarşamba günü sınıfa katılım 20, Cumartesi ise 15'tir. Bu değerler tek tek ve ayrı ayrı düşünülebilir, dolayısıyla şöyle adlandırılırlar.discrete values.

Yalnızca 1'ler ve 0'lara sahip olan ikili rakamlar çoğunlukla şu şekilde adlandırılır: digital values. Bu nedenle, 1'leri ve 0ları temsil eden sinyaller aynı zamandadigital signals. Dijital sinyaller ve dijital değerlere dayalı iletişime,Digital Communication.

Periyodik Sinyal

Modelini belirli bir süre boyunca tekrarlayan herhangi bir analog veya dijital sinyale, Periodic Signal. Bu sinyalin deseni tekrar tekrar devam ettirilir ve varsayılması veya hesaplanması kolaydır.

Misal

Sanayide bir makineyi düşünecek olursak, birbiri ardına gerçekleşen süreç sürekli bir süreçtir. Örneğin, hammaddenin temini ve derecelendirilmesi, malzemenin partiler halinde işlenmesi, bir ürün yükünün arka arkaya paketlenmesi vb. Belirli bir prosedürü tekrar tekrar izler.

İster analog ister dijital olarak değerlendirilsin böyle bir işlem aşağıdaki gibi grafiksel olarak temsil edilebilir.

Periyodik Sinyal

Modelini belirli bir süre boyunca tekrar etmeyen herhangi bir analog veya dijital sinyale Aperiodic Signal. Bu sinyalin paterni devam ettirilir, ancak model tekrarlanmaz. Ayrıca varsayılması veya hesaplanması o kadar da kolay değil.

Misal

Bir kişinin günlük rutini, dikkate alınırsa, farklı görevler için farklı zaman aralıkları alan çeşitli iş türlerinden oluşur. Zaman aralığı veya iş sürekli tekrar etmiyor. Örneğin, bir kişi sabahtan akşama kadar aynı zaman diliminde dişlerini sürekli fırçalamayacaktır.

İster analog ister dijital olarak değerlendirilsin böyle bir işlem aşağıdaki gibi grafiksel olarak temsil edilebilir.

Genelde iletişim sistemlerinde kullanılan sinyaller, ihtiyaca göre analog olarak iletilen veya dijitale dönüştürülen ve daha sonra iletilen doğası gereği analogdur.

Bir sinyalin herhangi bir dış parazit veya gürültü ilavesinin etkisi olmadan ve solmadan bir mesafeye iletilmesi için, adı verilen bir işlemden geçmesi gerekir. Modulation. Orijinal sinyalin parametrelerini bozmadan sinyalin gücünü artırır.

Modülasyon nedir?

Bir sinyal taşıyan bir mesajın belirli bir mesafeden iletilmesi gerekir ve güvenilir bir iletişim kurması için, mesaj sinyalinin orijinal özelliklerini etkilememesi gereken yüksek frekanslı bir sinyalden yardım alması gerekir.

Mesaj sinyalinin özellikleri, değiştirilirse, içerdiği mesaj da değişir. Bu nedenle, mesaj sinyaline dikkat etmek bir zorunluluktur. Yüksek frekanslı bir sinyal, harici parazitlerden etkilenmeden daha uzun bir mesafeye kadar gidebilir. Bu kadar yüksek frekanslı sinyalin yardımını alıyoruz.carrier signalmesaj sinyalimizi iletmek için. Böyle bir süreç basitçe Modülasyon olarak adlandırılır.

Modülasyon, modüle edici sinyalin anlık değerlerine göre taşıyıcı sinyalin parametrelerini değiştirme işlemidir.

Modülasyon İhtiyacı

Temel bant sinyalleri doğrudan iletim için uyumsuzdur. Böyle bir sinyal için, daha uzun mesafeler kat etmek için, modüle edici sinyalin parametrelerini etkilemeyen yüksek frekanslı bir taşıyıcı dalga ile modüle edilerek gücünün artırılması gerekir.

Modülasyonun Avantajları

Modülasyon uygulanmamışsa, iletim için kullanılan anten çok büyük olmalıydı. Dalga bozulmadan bir mesafeyi katedemeyeceği için iletişim alanı sınırlanır.

Aşağıda, iletişim sistemlerinde modülasyonu uygulamanın avantajlarından bazıları verilmiştir.

• Anten boyutunun küçültülmesi
• Sinyal karışımı yok
• Artan iletişim aralığı
• Sinyallerin çoklanması
• Bant genişliği ayarlama imkanı
• İyileştirilmiş alım kalitesi

Modülasyon İşlemindeki Sinyaller

Aşağıda, modülasyon sürecindeki üç sinyal türü bulunmaktadır.

Mesaj veya Modülasyon Sinyali

İletilecek bir mesajı içeren sinyale, message signal. Bu, iletilmesi için modülasyon sürecinden geçmesi gereken bir temel bant sinyalidir. Bu nedenle, aynı zamandamodulating signal.

Taşıyıcı Sinyali

Belirli bir genliği, frekansı ve fazı olan ancak hiçbir bilgi içermeyen yüksek frekanslı sinyale, carrier signal. Boş bir sinyaldir ve sinyali modülasyondan sonra alıcıya taşımak için kullanılır.

Modüle edilmiş Sinyal

Modülasyon işleminden sonra ortaya çıkan sinyale bir modulated signal. Bu sinyal, modüle edici sinyal ve taşıyıcı sinyalin bir kombinasyonudur.

Modülasyon Türleri

Pek çok modülasyon türü vardır. Kullanılan modülasyon tekniklerine bağlı olarak, aşağıdaki şekilde gösterildiği gibi sınıflandırılırlar.

Modülasyon türleri genel olarak sürekli dalga modülasyonu ve darbe modülasyonu olarak sınıflandırılır.

Sürekli dalga Modülasyonu

Sürekli dalga modülasyonunda, taşıyıcı dalga olarak yüksek frekanslı bir sinüs dalgası kullanılır. Bu ayrıca genlik ve açı modülasyonuna bölünmüştür.

• Yüksek frekanslı taşıyıcı dalganın genliği, modüle edici sinyalin anlık genliğine göre değiştirilirse, böyle bir teknik denir. Amplitude Modulation.

• Taşıyıcı dalganın açısı modüle edici sinyalin anlık değerine göre değiştirilirse, böyle bir teknik denir. Angle Modulation. Açı modülasyonu ayrıca frekans modülasyonu ve faz modülasyonu olarak ikiye ayrılır.

  • Taşıyıcı dalganın frekansı, modüle edici sinyalin anlık değerine göre değiştirilirse, böyle bir teknik denir. Frequency Modulation.

  • Yüksek frekanslı taşıyıcı dalganın fazı, modülasyon sinyalinin anlık değerine göre değiştirilirse, böyle bir teknik denir. Phase Modulation.

Darbe Modülasyonu

Darbe modülasyonunda, bir taşıyıcı dalga olarak periyodik bir dikdörtgen darbeler dizisi kullanılır. Bu ayrıca analog ve dijital modülasyona bölünmüştür.

Analog modülasyon tekniğinde, bir darbenin genliği veya süresi veya konumu, temel bant modülasyon sinyalinin anlık değerlerine göre değiştirilirse, böyle bir teknik Darbe Genlik Modülasyonu (PAM) veya Darbe Süresi / Genişlik Modülasyonu (PDM) olarak adlandırılır. / PWM) veya Darbe Konum Modülasyonu (PPM).

Dijital modülasyonda, kullanılan modülasyon tekniği, analog sinyalin 1'ler ve 0'ların dijital formuna dönüştürüldüğü Darbe Kod Modülasyonudur (PCM). Sonuç, kodlanmış bir darbe dizisi olduğundan, buna PCM denir. Bu, Delta Modülasyonu (DM) olarak daha da geliştirilmiştir. Bu dijital modülasyon teknikleri, Dijital İletişim eğitimimizde tartışılmaktadır.

Sürekli bir dalga, herhangi bir aralık olmaksızın sürekli olarak devam eder ve bilgiyi içeren temel bant mesaj sinyalidir. Bu dalganın modüle edilmesi gerekiyor.

Standart tanıma göre, "Taşıyıcı sinyalin genliği, modüle edici sinyalin anlık genliğine göre değişir." Yani, bilgi içermeyen taşıyıcı sinyalin genliği, bilgi içeren sinyalin her an genliğine göre değişir. Bu, aşağıdaki şekillerle iyi bir şekilde açıklanabilir.

İlk şekil, mesaj sinyali olan modüle edici dalgayı gösterir. Bir sonraki, yüksek frekanslı bir sinyal olan ve hiçbir bilgi içermeyen taşıyıcı dalgadır. Sonuncusu, sonuçta oluşan modüle edilmiş dalgadır.

Taşıyıcı dalganın pozitif ve negatif zirvelerinin hayali bir çizgi ile birbirine bağlı olduğu gözlemlenebilir. Bu çizgi, modülasyon sinyalinin tam şeklini yeniden oluşturmaya yardımcı olur. Taşıyıcı dalga üzerindeki bu hayali çizgiyeEnvelope. Mesaj sinyalininki ile aynıdır.

Matematiksel İfadeler

Bu dalgalar için matematiksel ifadeler aşağıdadır.

Dalgaların Zaman Alan Temsili

Modüle edici sinyal olsun,

$$ m \ left (t \ sağ) = A_m \ cos \ left (2 \ pi f_mt \ sağ) $$

ve taşıyıcı sinyal,

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Nerede,

$ A_m $ ve $ A_c $ sırasıyla modüle edici sinyalin ve taşıyıcı sinyalin genliğidir.

$ f_m $ ve $ f_c $ sırasıyla modüle edici sinyalin ve taşıyıcı sinyalin frekansıdır.

Ardından, Genlik Modülasyonlu dalganın denklemi

$ s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ right) $ (Denklem 1)

Modülasyon endeksi

Bir taşıyıcı dalga, modüle edildikten sonra, modüle edilmiş seviye hesaplanırsa, böyle bir girişim olarak adlandırılır. Modulation Index veya Modulation Depth. Bir taşıyıcı dalganın maruz kaldığı modülasyon seviyesini belirtir.

Denklem 1'i aşağıdaki gibi yeniden düzenleyin.

$ s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ sağ) \ cos \ left (2 \ pi f_mt \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $

$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ right) $ ( Denklem 2)

$ \ Mu $, Modülasyon indeksidir ve $ A_m $ ve $ A_c $ oranına eşittir. Matematiksel olarak şöyle yazabiliriz

$ \ mu = \ frac {A_m} {A_c} $ (Denklem 3)

Dolayısıyla, mesaj ve taşıyıcı sinyallerin genlikleri bilindiğinde, yukarıdaki formülü kullanarak modülasyon indeksinin değerini hesaplayabiliriz.

Şimdi, Denklem 1'i dikkate alarak Modülasyon indeksi için bir formül daha türetelim. Bu formülü, modüle edilmiş dalganın maksimum ve minimum genlikleri bilindiğinde modülasyon indeksi değerini hesaplamak için kullanabiliriz.

$ A_ \ max $ ve $ A_ \ min $, modüle edilmiş dalganın maksimum ve minimum genlikleri olsun.

$ \ Cos \ left (2 \ pi f_mt \ right) $ 1 olduğunda, modüle edilmiş dalganın maksimum genliğini alacağız.

$ \ Rightarrow A_ \ max = A_c + A_m $ (Denklem 4)

$ \ Cos \ left (2 \ pi f_mt \ right) $ -1 olduğunda, modüle edilmiş dalganın minimum genliğini alacağız.

$ \ Rightarrow A_ \ min = A_c - A_m $ (Denklem 5)

Denklem 4 ve Denklem 5'i ekleyin.

$$ A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c $$

$ \ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2} $ (Denklem 6)

Denklem 5'i Denklem 4'ten çıkarın.

$$ A_ \ max - A_ \ min = A_c + A_m - \ left (A_c -A_m \ sağ) = 2A_m $$

$ \ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2} $ (Denklem 7)

Denklem 7 ve Denklem 6'nın oranı aşağıdaki gibi olacaktır.

$$ \ frac {A_m} {A_c} = \ frac {\ left (A_ {max} - A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ sağ) / 2 } $$

$ \ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min} $ (Denklem 8)

Bu nedenle, Denklem 3 ve Denklem 8, Modülasyon indeksi için iki formüldür. Modülasyon indeksi veya modülasyon derinliği, genellikle Modülasyon Yüzdesi olarak adlandırılan yüzde olarak belirtilir. Alacağızpercentage of modulation, sadece modülasyon indeksi değerini 100 ile çarparak.

Mükemmel bir modülasyon için, modülasyon indeksinin değeri 1 olmalıdır, bu da modülasyon yüzdesinin% 100 olması gerektiği anlamına gelir.

Örneğin, bu değer 1'den küçükse, yani modülasyon indeksi 0.5 ise, modüle edilmiş çıktı aşağıdaki şekle benzeyecektir. Olarak adlandırılırUnder-modulation. Böyle bir dalgaya birunder-modulated wave.

Modülasyon indeksinin değeri 1'den büyükse, yani 1.5 veya daha fazla ise, dalga bir over-modulated wave. Aşağıdaki şekle benzeyecektir.

Modülasyon indeksinin değeri arttıkça, taşıyıcı 180 ^{derecelik bir} faz dönüşü yaşar , bu da ek yan bantlara neden olur ve dolayısıyla dalga deforme olur. Böyle aşırı modüle edilmiş bir dalga, ortadan kaldırılamayan girişime neden olur.

AM Dalgasının Bant Genişliği

Bandwidth(BW), sinyalin en yüksek ve en düşük frekansları arasındaki farktır. Matematiksel olarak şöyle yazabiliriz

$$ BW = f_ {maks} - f_ {min} $$

Aşağıdaki genlik modülasyonlu dalga denklemini düşünün.

$$ s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$

$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ sağ) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $

Dolayısıyla, genlik modülasyonlu dalganın üç frekansı vardır. Bunlar taşıyıcı frekansı $ f_c $, üst yan bant frekansı $ f_c + f_m $ ve alt yan bant frekansı $ f_c-f_m $

Buraya,

$ f_ {max} = f_c + f_m $ ve $ f_ {min} = f_c-f_m $

Bant genişliği formülündeki $ f_ {max} $ ve $ f_ {min} $ değerlerini değiştirin.

$$ BW = f_c + f_m- \ left (f_c-f_m \ sağ) $$

$$ \ Rightarrow BW = 2f_m $$

Bu nedenle, genlik modülasyonlu dalga için gereken bant genişliğinin modüle edici sinyalin frekansının iki katı olduğu söylenebilir.

AM Dalgasının Güç Hesaplamaları

Aşağıdaki genlik modülasyonlu dalga denklemini düşünün.

$ \ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ sağ) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $

AM dalgasının gücü, taşıyıcı, üst yan bant ve alt yan bant frekans bileşenlerinin güçlerinin toplamına eşittir.

$$ P_t = P_c + P_ {USB} + P_ {LSB} $$

Cos sinyalinin gücü için standart formülün olduğunu biliyoruz

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2} $$

Nerede,

$ v_ {rms} $, cos sinyalinin rms değeridir.

$ v_m $, cos sinyalinin tepe değeridir.

Önce taşıyıcının, üst ve alt yan bandın güçlerini tek tek bulalım.

Taşıyıcı gücü

$$ P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R} $$

Üst yan bant gücü

$$ P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Benzer şekilde, alt yan bant gücünü üst yan bant gücüyle aynı şekilde alacağız.

$$ P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

Şimdi, AM dalgasının gücünü elde etmek için bu üç gücü ekleyelim.

$$ P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ sağ) $$

$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ sağ) $$

Taşıyıcı güç ve modülasyon indeksi bilindiğinde, AM dalgasının gücünü hesaplamak için yukarıdaki formülü kullanabiliriz.

Modülasyon indeksi $ \ mu = 1 $ ise AM dalgasının gücü taşıyıcı gücün 1.5 katına eşittir. Dolayısıyla, bir AM dalgasını iletmek için gereken güç, mükemmel bir modülasyon için taşıyıcı gücün 1,5 katıdır.

Önceki bölümde, Genlik Modülasyonunda kullanılan parametreleri tartışmıştık. Her parametrenin kendi formülü vardır. Bu formülleri kullanarak, ilgili parametre değerlerini bulabiliriz. Bu bölümde, genlik modülasyonu kavramına dayalı birkaç problemi çözelim.

Problem 1

$ M \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $ modüle edici bir sinyal, genlik modüle edilmiş bir taşıyıcı sinyal $ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5 t \ right) $. Modülasyon indeksini, taşıyıcı gücü ve AM dalgasını iletmek için gereken gücü bulun.

Çözüm

Verildiğinde, sinyali modüle etme denklemi

$$ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $$

Sinyal modülasyonunun standart denklemini şu şekilde biliyoruz:

$$ m \ left (t \ sağ) = A_m \ cos \ left (2 \ pi f_mt \ sağ) $$

Yukarıdaki iki denklemi karşılaştırarak elde edeceğiz

Modülasyon sinyalinin genliği $ A_m = 10 volt $ olarak

ve $$ f_m = 10 ^ 3 Hz = 1 KHz $$ olarak sinyal modülasyon frekansı

Verildiğinde, taşıyıcı sinyalin denklemi

$$ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5t \ right) $$

Taşıyıcı sinyalin standart denklemi

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Bu iki denklemi karşılaştırarak elde edeceğiz

Taşıyıcı sinyalin $ A_c = 50volts $ olarak genliği

ve $ f_c = 10 ^ 5 Hz = 100 KHz $ olarak taşıyıcı sinyalin frekansı

Modülasyon indeksi formülünü şu şekilde biliyoruz:

$$ \ mu = \ frac {A_m} {A_c} $$

Yukarıdaki formülde, $ A_m $ ve $ A_c $ değerlerini değiştirin.

$$ \ mu = \ frac {10} {50} = 0.2 $$

Bu nedenle, değeri modulation index is 0.2 ve modülasyon yüzdesi% 20'dir.

Taşıyıcı gücünün formülü, $ P_c = $ şudur:

$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$

$ R = 1 \ Omega $ kabul edin ve yukarıdaki formülde $ A_c $ değerini değiştirin.

$$ P_c = \ frac {\ left (50 \ sağ) ^ 2} {2 \ left (1 \ right)} = 1250W $$

bu yüzden Carrier power, $ P_c $ 1250 watts.

Formülünü biliyoruz power için gerekli olan transmitting AM dalga

$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ sağ) $$

Yukarıdaki formülde $ P_c $ ve $ \ mu $ değerlerini değiştirin.

$$ P_t = 1250 \ left (1+ \ frac {\ left (0,2 \ sağ) ^ 2} {2} \ sağ) = 1275 W $$

bu yüzden power required for transmitting AM dalga 1275 watts.

Problem 2

Genlik dalgasının denklemi $ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $. AM dalgasının taşıyıcı gücünü, toplam yan bant gücünü ve bant genişliğini bulun.

Çözüm

Verilen, Genlik modülasyonlu dalganın denklemi

$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $$

Yukarıdaki denklemi şu şekilde yeniden yazın:

$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (2 \ pi \ times 2 \ times 10 ^ 5t \ sağ) $$

Genlik modülasyonlu dalganın denkleminin

$$ s \ left (t \ right) = A_c \ left [1+ \ mu \ cos \ left (2 \ pi f_mt \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

Yukarıdaki iki denklemi karşılaştırarak elde edeceğiz

Taşıyıcı sinyalin genliği $ A_c = 20 volt $ olarak

$ \ Mu = 0.8 $ olarak modülasyon indeksi

$ F_m = 10 ^ 3Hz = 1 KHz $ olarak sinyal modülasyon frekansı

Taşıyıcı sinyalinin $ f_c = 2 \ times 10 ^ 5Hz = 200KHz $ olarak frekansı

Taşıyıcı gücünün formülü, $ P_c $

$$ P_c = \ frac {{A_ {e}} ^ {2}} {2R} $$

$ R = 1 \ Omega $ kabul edin ve yukarıdaki formülde $ A_c $ değerini değiştirin.

$$ P_c = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$

bu yüzden Carrier power, $ P_c $ 200watts.

Toplam yan bant gücünün formülünü biliyoruz

$$ P_ {SB} = \ frac {P_c \ mu ^ 2} {2} $$

Yukarıdaki formülde $ P_c $ ve $ \ mu $ değerlerini değiştirin.

$$ P_ {SB} = \ frac {200 \ times \ left (0,8 \ sağ) ^ 2} {2} = 64W $$

bu yüzden total side band power dır-dir 64 watts.

AM dalgasının bant genişliği formülünün

$$ BW = 2f_m $$

Yukarıdaki formülde $ f_m $ değerini değiştirin.

$$ BW = 2 \ sol (1K \ sağ) = 2 KHz $$

bu yüzden bandwidth AM dalgası 2 KHz.

Bu bölümde, genlik modülasyonlu dalga üreten modülatörlerden bahsedelim. Aşağıdaki iki modülatör AM dalgası oluşturur.

• Kare hukuku modülatörü
• Anahtarlama modülatörü

Kare Hukuk Modülatörü

Kare kanunu modülatörünün blok diyagramı aşağıdadır

Modüle edici ve taşıyıcı sinyaller sırasıyla $ m \ left (t \ right) $ ve $ A \ cos \ left (2 \ pi f_ct \ right) $ olarak gösterilsin. Bu iki sinyal, yaz (toplayıcı) bloğuna girişler olarak uygulanır. Bu yaz bloğu, modülasyon ve taşıyıcı sinyalin eklenmesi olan bir çıktı üretir. Matematiksel olarak şöyle yazabiliriz

$$ V_1t = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Bu sinyal $ V_1t $, diyot gibi doğrusal olmayan bir cihaza bir girdi olarak uygulanır. Diyotun özellikleri, kare yasasıyla yakından ilgilidir.

$ V_2t = k_1V_1 \ left (t \ sağ) + k_2V_1 ^ 2 \ left (t \ right) $ (Denklem 1)

Burada, $ k_1 $ ve $ k_2 $ sabittir.

Denklem 1'deki $ V_1 \ left (t \ right) $ 'ı değiştirin

$$ V_2 \ sol (t \ sağ) = k_1 \ sol [m \ sol (t \ sağ) + A_c \ cos \ left (2 \ pi f_ct \ sağ) \ sağ] + k_2 \ sol [m \ sol (t \ sağ) + A_c \ cos \ left (2 \ pi f_ct \ sağ) \ sağ] ^ 2 $$

$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ sağ) + k_2 m ^ 2 \ left (t \ sağ) + $

$ k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ sağ) + k_2 m ^ 2 \ left (t \ sağ) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ sağ) + $

$ k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ sağ) m \ left (t \ right) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $

Yukarıdaki denklemin son terimi istenen AM dalgasını temsil eder ve yukarıdaki denklemin ilk üç terimi istenmez. Yani bant geçiren filtre yardımıyla sadece AM dalgasını geçip ilk üç terimi ortadan kaldırabiliriz.

Bu nedenle, kare kanunu modülatörünün çıktısı

$$ s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ sağ) m \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ right) $$

AM dalgasının standart denklemi

$$ s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

$ K_a $ genlik hassasiyetidir

Kare kanunu modülatörünün çıktısını AM dalgasının standart denklemi ile karşılaştırarak, ölçeklendirme faktörünü $ k_1 $ ve genlik duyarlılığını $ k_a $ $ \ frac {2k_2} {k1} $ olarak alacağız.

Anahtarlama Modülatörü

Anahtarlama modülatörünün blok şeması aşağıdadır.

Anahtarlama modülatörü kare kanunu modülatörüne benzer. Tek fark, kare kanunu modülatöründe diyotun doğrusal olmayan bir modda çalıştırılması, anahtarlama modülatöründe ise diyotun ideal bir anahtar olarak çalışması gerektiğidir.

Modüle edici ve taşıyıcı sinyaller sırasıyla $ m \ left (t \ right) $ ve $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ olarak gösterilsin. Bu iki sinyal, yaz (toplayıcı) bloğuna girişler olarak uygulanır. Yaz bloğu, modülasyon ve taşıyıcı sinyallerin eklenmesi olan bir çıktı üretir. Matematiksel olarak şöyle yazabiliriz

$$ V_1 \ left (t \ sağ) = m \ left (t \ right) + c \ left (t \ sağ) = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ sağ ) $$

Bu $ V_1 \ left (t \ right) $ sinyali, bir diyot girişi olarak uygulanır. Farz edelim ki, modüle edici sinyalin büyüklüğü, taşıyıcı sinyal $ A_c $ genliği ile karşılaştırıldığında çok küçük. Dolayısıyla, diyotun AÇIK ve KAPALI eylemi $ c \ left (t \ right) $ taşıyıcı sinyali tarafından kontrol edilir. Bu, diyotun $ c \ left (t \ right)> 0 $ olduğunda ileriye doğru önyargılı olacağı ve $ c \ left (t \ right) <0 $ olduğunda ters önyargılı olacağı anlamına gelir.

Bu nedenle, diyotun çıkışı

$$ V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ sağ) <0 \ end {matris} \ sağ. $$

Buna şu şekilde yaklaşabiliriz

$ V_2 \ left (t \ sağ) = V_1 \ sol (t \ sağ) x \ left (t \ sağ) $ (Denklem 2)

$ X \ left (t \ right) $, $ T = \ frac {1} {f_c} $ zaman periyodu olan periyodik bir darbeli dizidir

Bu periyodik darbe dizisinin Fourier serisi temsili

$$ x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ sağ) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ sağ) $$

$$ \ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + .... $$

Denklem 2'deki $ V_1 \ left (t \ right) $ ve $ x \ left (t \ right) $ değerlerini değiştirin.

$ V_2 \ sol (t \ sağ) = \ sol [m \ sol (t \ sağ) + A_c \ cos \ left (2 \ pi f_ct \ sağ) \ sağ] \ sol [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ right] $

$ V_2 \ left (t \ sağ) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ sağ) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ sağ) \ cos \ left (6 \ pi f_ct \ sağ) + ..... $

$ V_2 \ left (t \ sağ) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ sağ) m \ left (t \ sağ) \ sağ) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ sağ) - $

$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ sağ) \ cos \ left (6 \ pi f_ct \ sağ) + ..... $

1 ^st Yukarıdaki denklemin terimi arzu edilen PM dalga temsil eder ve geri kalan terimler istenmeyen terimlerdir. Böylece bant geçiren filtre yardımı ile sadece AM dalgasını geçip kalan terimleri ortadan kaldırabiliyoruz.

Bu nedenle, anahtarlama modülatörünün çıkışı

$$ s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ sağ) m \ left (t \ sağ) \ sağ ) \ cos \ left (2 \ pi f_ct \ right) $$

AM dalgasının standart denkleminin olduğunu biliyoruz

$$ s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

$ K_a $, genlik duyarlılığıdır.

Anahtarlama modülatörünün çıktısını AM dalgasının standart denklemi ile karşılaştırarak, ölçeklendirme faktörünü 0.5 ve genlik duyarlılığını $ k_a $ $ \ frac {4} {\ pi A_c} $ olarak alacağız.

Modüle edilmiş dalgadan orijinal bir mesaj sinyali çıkarma işlemi olarak bilinir. detection veya demodulation. Modüle edilmiş dalgayı demodüle eden devre,demodulator. Aşağıdaki demodülatörler (dedektörler) AM dalgasını demodüle etmek için kullanılır.

• Kare Hukuk Demodülatörü
• Zarf Detektörü

Kare Hukuk Demodülatörü

Kare yasa demodülatörü, düşük seviyeli AM dalgasını demodüle etmek için kullanılır. Aşağıdakilerin blok diyagramısquare law demodulator.

Bu demodülatör, bir kare kanun cihazı ve alçak geçiren filtre içerir. $ V_1 \ left (t \ right) $ AM dalgası, bu demodülatöre bir girdi olarak uygulanır.

AM dalgasının standart şekli

$$ V_1 \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

Kare kanun cihazının girişi ve çıkışı arasındaki matematiksel ilişkinin olduğunu biliyoruz.

$ V_2 \ left (t \ sağ) = k_1V_1 \ left (t \ sağ) + k_2V_1 ^ 2 \ left (t \ right) $ (Denklem 1)

Nerede,

$ V_1 \ left (t \ right) $, AM dalgasından başka bir şey olmayan kare yasası aygıtının girdisidir

$ V_2 \ left (t \ right) $, kare yasası aygıtının çıktısıdır

$ k_1 $ ve $ k_2 $ sabittir

Denklem 1'deki $ V_1 \ left (t \ right) $ 'ı değiştirin

$$ V_2 \ left (t \ sağ) = k_1 \ left (A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) \ sağ) + k_2 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ sağ) \ sağ) ^ 2 $$

$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + $

$ k_2 {A_ {c}} ^ {2} \ left [1+ {K_ {a}} ^ {2} m ^ 2 \ left (t \ sağ) + 2k_am \ left (t \ sağ) \ sağ] \ sol (\ frac {1+ \ cos \ left (4 \ pi f_ct \ sağ)} {2} \ sağ) $

$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {c}} ^ {2}} {2} + $

$ \ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ left (t \ right)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ left (t \ sağ)} {2} \ cos \ left (4 \ pi f_ct \ sağ) + $

$ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) + k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) \ cos \ left (4 \ pi f_ct \ sağ) $

Yukarıdaki denklemde, $ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) $ terimi, mesaj sinyalinin ölçeklendirilmiş halidir. Yukarıdaki sinyali bir alçak geçiren filtreden geçirerek çıkarılabilir ve DC bileşeni $ \ frac {k_2 {A_ {c}} ^ {2}} {2} $ bir bağlantı kapasitörünün yardımıyla elimine edilebilir.

Zarf Detektörü

Zarf detektörü, yüksek seviyeli AM dalgasını tespit etmek (demodüle etmek) için kullanılır. Zarf detektörünün blok diyagramı aşağıdadır.

Bu zarf detektörü bir diyot ve alçak geçiren filtreden oluşur. Burada diyot, ana tespit elemanıdır. Bu nedenle, zarf algılayıcısı aynı zamandadiode detector. Düşük geçiş filtresi, direnç ve kapasitörün paralel bir kombinasyonunu içerir.

$ S \ left (t \ right) $ AM dalgası, bu detektöre bir girdi olarak uygulanır.

AM dalgasının standart biçiminin

$$ s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

AM dalgasının pozitif yarı döngüsünde, diyot iletken olur ve kapasitör, AM dalgasının tepe değerine yüklenir. AM dalgasının değeri bu değerin altına düştüğünde diyot ters taraflı olacaktır. Böylece, kondansatör direnç yoluyla deşarj olacaktır.RAM dalgasının bir sonraki pozitif yarı döngüsüne kadar. AM dalgasının değeri kondansatör voltajından büyük olduğunda diyot iletir ve işlem tekrarlanır.

Bileşen değerlerini, kapasitörün çok hızlı şarj olacağı ve çok yavaş deşarj olacağı şekilde seçmeliyiz. Sonuç olarak, neredeyse modülasyon sinyaline benzeyen AM dalgası zarfınınki ile aynı kapasitör voltaj dalga formunu elde edeceğiz.

Genlik Modülasyonu sürecinde, modüle edilmiş dalga, taşıyıcı dalgadan ve iki yan banttan oluşur. Modüle edilmiş dalga, yalnızca yan bantlarda bilgi içerir.Sideband taşıyıcı frekansın düşük ve yüksek frekansları olan gücü içeren bir frekanslar bandından başka bir şey değildir.

İki yan bant ile birlikte bir taşıyıcı içeren bir sinyalin iletimi şu şekilde adlandırılabilir: Double Sideband Full Carrier sistem veya basitçe DSBFC. Aşağıdaki şekilde gösterildiği gibi çizilmiştir.

Ancak böyle bir iletim verimsizdir. Çünkü hiçbir bilgi taşımayan taşıyıcıda gücün üçte ikisi boşa gidiyor.

Bu taşıyıcı bastırılırsa ve tasarruf edilen güç iki yan banda dağıtılırsa, böyle bir işlem olarak adlandırılır. Double Sideband Suppressed Carrier sistem veya basitçe DSBSC. Aşağıdaki şekilde gösterildiği gibi çizilmiştir.

Matematiksel İfadeler

Önceki bölümlerde ele aldığımız gibi, modülasyon ve taşıyıcı sinyaller için aynı matematiksel ifadeleri ele alalım.

yani Modülasyon sinyali

$$ m \ left (t \ sağ) = A_m \ cos \ left (2 \ pi f_mt \ sağ) $$

Taşıyıcı sinyali

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Matematiksel olarak, temsil edebiliriz equation of DSBSC wave modülasyon ve taşıyıcı sinyallerin ürünü olarak.

$$ s \ left (t \ sağ) = m \ sol (t \ sağ) c \ sol (t \ sağ) $$

$$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$

DSBSC Wave Bant Genişliği

Bant genişliği formülünün (BW) olduğunu biliyoruz

$$ BW = f_ {maks} -f_ {min} $$

DSBSC modüle edilmiş dalganın denklemini düşünün.

$$ s \ left (t \ sağ) = A_mA_c \ cos \ left (2 \ pi f_mt \ sağ) \ cos (2 \ pi f_ct) $$

$$ \ Rightarrow s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $$

DSBSC ile modüle edilmiş dalganın yalnızca iki frekansı vardır. Dolayısıyla, maksimum ve minimum frekanslar sırasıyla $ f_c + f_m $ ve $ f_c-f_m $ şeklindedir.

yani

$ f_ {max} = f_c + f_m $ ve $ f_ {min} = f_c-f_m $

Bant genişliği formülündeki $ f_ {max} $ ve $ f_ {min} $ değerlerini değiştirin.

$$ BW = f_c + f_m- \ left (f_c-f_m \ sağ) $$

$$ \ Rightarrow BW = 2f_m $$

Böylece, DSBSC dalgasının bant genişliği AM dalgasının bant genişliği ile aynıdır ve modüle edici sinyalin frekansının iki katına eşittir.

DSBSC Wave'in Güç Hesaplamaları

Aşağıdaki DSBSC modüle dalganın denklemini düşünün.

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] + \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $$

DSBSC dalgasının gücü, üst yan bant ve alt yan bant frekans bileşenlerinin güçlerinin toplamına eşittir.

$$ P_t = P_ {USB} + P_ {LSB} $$

Cos sinyalinin gücü için standart formülün

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R} $$

Öncelikle üst yan bandın ve alt yan bandın güçlerini tek tek bulalım.

Üst yan bant gücü

$$ P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Benzer şekilde, alt yan bant gücünü üst yan bant gücüyle aynı şekilde alacağız.

$$ P_ {USB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Şimdi, DSBSC dalgasının gücünü elde etmek için bu iki yan bant gücünü ekleyelim.

$$ P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} + \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

$$ \ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R} $$

Bu nedenle, DSBSC dalgasını iletmek için gereken güç, her iki yan bandın gücüne eşittir.

Bu bölümde, DSBSC dalgasını oluşturan modülatörler hakkında tartışalım. Aşağıdaki iki modülatör DSBSC dalgasını oluşturur.

• Dengeli modülatör
• Halka modülatörü

Dengeli Modülatör

Dengeli modülatörün blok şeması aşağıdadır.

Balanced modulatoriki özdeş AM modülatöründen oluşur. Bu iki modülatör, taşıyıcı sinyali bastırmak için dengeli bir konfigürasyonda düzenlenmiştir. Bu nedenle, Dengeli modülatör olarak adlandırılır.

Aynı taşıyıcı sinyal $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $, bu iki AM modülatörüne girişlerden biri olarak uygulanır. $ M \ left (t \ right) $ modülasyon sinyali, üst AM modülatörüne başka bir girdi olarak uygulanır. Oysa karşıt kutuplu $ m \ left (t \ right) $ modülasyon sinyali, yani $ -m \ left (t \ right) $, alt AM modülatörüne başka bir girdi olarak uygulanır.

Üst AM modülatörünün çıkışı

$$ s_1 \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

Alt AM modülatörünün çıkışı

$$ s_2 \ left (t \ sağ) = A_c \ left [1-k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

$ S_1 \ left (t \ right) $ 'dan $ s_2 \ left (t \ right) $ çıkararak DSBSC dalgasını $ s \ left (t \ right) $ elde ederiz. Yaz bloğu bu işlemi gerçekleştirmek için kullanılır. Pozitif işaretli $ s_1 \ left (t \ right) $ ve eksi işaretli $ s_2 \ left (t \ right) $ yaz bloğuna girdi olarak uygulanır. Böylece, yaz bloğu $ s_1 \ left (t \ right) $ ve $ s_2 \ left (t \ right) $ arasındaki fark olan $ s \ left (t \ right) $ çıktısını üretir.

$$ \ Rightarrow s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ sağ) -A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ sağ) $$

$$ \ Rightarrow s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) + A_ck_am \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) - A_c \ cos \ left (2 \ pi f_ct \ sağ) + $$

$ A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $

DSBSC dalgasının standart denkleminin olduğunu biliyoruz

$$ s \ left (t \ sağ) = A_cm \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$

Yaz bloğunun çıktısını DSBSC dalgasının standart denklemi ile karşılaştırarak, ölçeklendirme faktörünü $ 2k_a $ olarak alacağız.

Halka Modülatör

Halka modülatörünün blok şeması aşağıdadır.

Bu diyagramda, dört diyot $ D_1 $, $ D_2 $, $ D_3 $ ve $ D_4 $ halka yapısında bağlıdır. Bu nedenle, bu modülatörering modulator. Bu diyagramda iki adet orta kademeli transformatör kullanılmıştır. $ M \ left (t \ right) $ mesaj sinyali giriş trafosuna uygulanır. Oysa, taşıyıcı sinyaller $ c \ left (t \ right) $ iki merkeze bağlı transformatör arasına uygulanır.

Taşıyıcı sinyalin pozitif yarı döngüsü için, $ D_1 $ ve $ D_3 $ diyotları AÇIK konuma getirilir ve diğer iki diyot $ D_2 $ ve $ D_4 $ KAPALI konuma getirilir. Bu durumda mesaj sinyali +1 ile çarpılır.

Taşıyıcı sinyalin negatif yarı döngüsü için, $ D_2 $ ve $ D_4 $ diyotları AÇIK konuma getirilir ve diğer iki diyot $ D_1 $ ve $ D_3 $ KAPALI konuma getirilir. Bu durumda, mesaj sinyali -1 ile çarpılır. Bu, ortaya çıkan DSBSC dalgasında 180 $ ^ 0 $ faz kayması ile sonuçlanır.

Yukarıdaki analizden, $ D_1 $, $ D_2 $, $ D_3 $ ve $ D_4 $ diyotlarının taşıyıcı sinyal tarafından kontrol edildiğini söyleyebiliriz. Taşıyıcı bir kare dalgaysa, $ c \ left (t \ right) $ 'ın Fourier serisi gösterimi şu şekilde temsil edilir:

$$ c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ sağ] $$

$ C \ left (t \ right) $ taşıyıcı sinyalinin ve $ m \ left (t \ right) $ ie mesaj sinyalinin ürünü olan DSBSC dalgasını $ s \ left (t \ right) $ alacağız. ,

$$ s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ sağ] m \ left (t \ sağ) $$

Yukarıdaki denklem, halka modülatörünün çıkış transformatöründe elde edilen DSBSC dalgasını temsil eder.

DSBSC modülatörleri aynı zamanda product modulators iki giriş sinyalinin ürünü olan çıkışı ürettikleri için.

DSBSC dalgasından orijinal bir mesaj sinyali çıkarma işlemi, DSBSC'nin tespiti veya demodülasyonu olarak bilinir. Aşağıdaki demodülatörler (dedektörler) DSBSC dalgasını demodüle etmek için kullanılır.

• Tutarlı Dedektör
• Costas Döngüsü

Tutarlı Dedektör

Burada, mesaj sinyalini tespit etmek için (DSBSC sinyali oluşturmak için kullanılan) aynı taşıyıcı sinyal kullanılır. Bu nedenle, bu tespit sürecinecoherent veya synchronous detection. Tutarlı detektörün blok şeması aşağıdadır.

Bu süreçte, mesaj sinyali DSBSC dalgasından aynı frekansa ve DSBSC modülasyonunda kullanılan taşıyıcının fazına sahip bir taşıyıcıyla çarpılarak çıkarılabilir. Ortaya çıkan sinyal daha sonra bir Düşük Geçiş Filtresinden geçirilir. Bu filtrenin çıktısı istenen mesaj sinyalidir.

DSBSC dalgası

$$ s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) $$

Yerel osilatörün çıkışı

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

$ \ Phi $, yerel osilatör sinyali ile DSBSC modülasyonu için kullanılan taşıyıcı sinyal arasındaki faz farkıdır.

Şekilden ürün modülatörünün çıktısını şöyle yazabiliriz:

$$ v \ left (t \ sağ) = s \ sol (t \ sağ) c \ sol (t \ sağ) $$

Yukarıdaki denklemde $ s \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini değiştirin.

$$ \ Rightarrow v \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) A_c \ cos \ left (2 \ pi f_ct + \ phi \ sağ) $$

$ = {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ left (t \ right) $

$ = \ frac {{A_ {c}} ^ {2}} {2} \ left [\ cos \ left (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ left (t \ sağ) $

$$ v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ sağ) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$

Yukarıdaki denklemde, ilk terim, mesaj sinyalinin ölçekli versiyonudur. Yukarıdaki sinyali bir düşük geçiş filtresinden geçirerek çıkarılabilir.

Bu nedenle, alçak geçiren filtrenin çıkışı

$$ v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) $$

Demodüle edilmiş sinyal genliği, $ \ phi = 0 ^ 0 $ olduğunda maksimum olacaktır. Bu nedenle yerel osilatör sinyali ile taşıyıcı sinyal fazda olmalıdır, yani bu iki sinyal arasında faz farkı olmamalıdır.

Demodüle edilmiş sinyal genliği, $ \ phi = \ pm 90 ^ 0 $ olduğunda sıfır olacaktır. Bu etkiyequadrature null effect.

Costas Döngüsü

Costas döngüsü, hem taşıyıcı sinyali (DSBSC modülasyonu için kullanılır) hem de yerel olarak üretilen sinyali fazda yapmak için kullanılır. Aşağıda, Costas döngüsünün blok diyagramı verilmiştir.

Costas looportak giriş $ s \ left (t \ right) $ olan iki ürün modülatöründen oluşur, bu DSBSC dalgasıdır. Her iki ürün modülatörü için diğer girdi,Voltage Controlled Oscillator (VCO), şekilde gösterildiği gibi ürün modülatörlerinden birine $ -90 ^ 0 $ faz kayması ile.

DSBSC dalgasının denkleminin olduğunu biliyoruz

$$ s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) $$

VCO'nun çıktısının

$$ c_1 \ left (t \ sağ) = \ cos \ left (2 \ pi f_ct + \ phi \ right) $$

Bu VCO çıkışı, üst ürün modülatörünün taşıyıcı girişi olarak uygulanır.

Dolayısıyla, üst ürün modülatörünün çıktısı

$$ v_1 \ sol (t \ sağ) = s \ sol (t \ sağ) c_1 \ sol (t \ sağ) $$

Yukarıdaki denklemde $ s \ left (t \ right) $ ve $ c_1 \ left (t \ right) $ değerlerini değiştirin.

$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $

Basitleştirdikten sonra, $ v_1 \ left (t \ right) $ as

$$ v_1 \ left (t \ sağ) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) + \ frac {A_c} {2} \ cos \ left (4 \ pi f_ct + \ phi \ sağ) m \ sol (t \ sağ) $$

Bu sinyal, üst düşük geçiş filtresinin bir girişi olarak uygulanır. Bu düşük geçiş filtresinin çıktısı

$$ v_ {01} \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) $$

Bu nedenle, bu düşük geçiş filtresinin çıkışı, modülasyon sinyalinin ölçeklendirilmiş versiyonudur.

$ -90 ^ 0 $ faz kaydırıcısının çıktısı

$$ c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right) $$

Bu sinyal, alt ürün modülatörünün taşıyıcı girişi olarak uygulanır.

Alt ürün modülatörünün çıktısı

$$ v_2 \ left (t \ sağ) = s \ sol (t \ sağ) c_2 \ sol (t \ sağ) $$

Yukarıdaki denklemde $ s \ left (t \ right) $ ve $ c_2 \ left (t \ right) $ değerlerini değiştirin.

$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $

Basitleştirdikten sonra, $ v_2 \ left (t \ right) $ as

$$ v_2 \ left (t \ sağ) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) + \ frac {A_c} {2} \ sin \ left (4 \ pi f_ct + \ phi \ sağ) m \ sol (t \ sağ) $$

Bu sinyal, düşük düşük geçiş filtresinin bir girişi olarak uygulanır. Bu düşük geçiş filtresinin çıktısı

$$ v_ {02} \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ sağ) $$

Bu Düşük geçiren filtrenin çıktısı, üst alçak geçiren süzgecin çıktısı ile -90 ^ 0 $ faz farkına sahiptir.

Bu iki düşük geçiş filtresinin çıkışları, faz ayırıcının girdileri olarak uygulanır. Bu iki sinyal arasındaki faz farkına bağlı olarak, faz ayırıcı bir DC kontrol sinyali üretir.

Bu sinyal, VCO çıkışındaki faz hatasını düzeltmek için bir VCO girişi olarak uygulanır. Bu nedenle, taşıyıcı sinyal (DSBSC modülasyonu için kullanılır) ve yerel olarak üretilen sinyal (VCO çıkışı) fazdadır.

Önceki bölümlerde, DSBSC modülasyonunu ve demodülasyonunu tartışmıştık. DSBSC ile modüle edilmiş sinyalin iki yan bandı vardır. İki yan bant aynı bilgiyi taşıdığından, her iki yan bandın da iletilmesine gerek yoktur. Bir yan bandı ortadan kaldırabiliriz.

Taşıyıcı ile birlikte yan bantlardan birini bastırma ve tek bir yan bandı iletme işlemine denir. Single Sideband Suppressed Carrier sistem veya basitçe SSBSC. Aşağıdaki şekilde gösterildiği gibi çizilmiştir.

Yukarıdaki şekilde, taşıyıcı ve alt yan bant bastırılmıştır. Dolayısıyla, iletim için üst yan bant kullanılır. Benzer şekilde, alt yan bandı iletirken taşıyıcıyı ve üst yan bandı bastırabiliriz.

Tek bir yan bandı ileten bu SSBSC sistemi, bu Tek Yan Bandın iletilmesinde hem taşıyıcı hem de diğer yan bant için ayrılan güçten yararlanıldığı için yüksek güce sahiptir.

Matematiksel İfadeler

Önceki bölümlerde ele aldığımız gibi, modülasyon ve taşıyıcı sinyaller için aynı matematiksel ifadeleri ele alalım.

yani Modülasyon sinyali

$$ m \ left (t \ sağ) = A_m \ cos \ left (2 \ pi f_mt \ sağ) $$

Taşıyıcı sinyali

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Matematiksel olarak, SSBSC dalgasının denklemini şu şekilde gösterebiliriz:

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ üst yan bant için

Veya

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ right] $ alt yan bant için

SSBSC Dalgasının Bant Genişliği

DSBSC ile modüle edilmiş dalganın iki yan bant içerdiğini ve bant genişliğinin $ 2f_m $ olduğunu biliyoruz. SSBSC ile modüle edilmiş dalga yalnızca bir yan bant içerdiğinden, bant genişliği DSBSC modüle edilmiş dalganın bant genişliğinin yarısıdır.

yani Bandwidth of SSBSC modulated wave = $ \ frac {2f_m} {2} = f_m $

Bu nedenle, SSBSC ile modüle edilmiş dalganın bant genişliği $ f_m $ 'dır ve modüle edici sinyalin frekansına eşittir.

SSBSC Dalgasının Güç Hesaplamaları

Aşağıdaki SSBSC ile modüle edilmiş dalganın denklemini düşünün.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ üst yan bant için

Veya

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ right] $ alt yan bant için

SSBSC dalgasının gücü, herhangi bir yan bant frekans bileşeninin gücüne eşittir.

$$ P_t = P_ {USB} = P_ {LSB} $$

Cos sinyalinin gücü için standart formülün olduğunu biliyoruz

$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R} $$

Bu durumda, üst yan bandın gücü

$$ P_ {USB} = \ frac {\ left (A_m A_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$

Benzer şekilde, alt yan bant gücünü üst yan bant gücüyle aynı şekilde alacağız.

$$ P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Bu nedenle, SSBSC dalgasının gücü

$$ P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$

Avantajlar

• Kaplanan bant genişliği veya spektrum alanı, AM ve DSBSC dalgalarından daha azdır.

• Daha fazla sayıda sinyalin iletilmesine izin verilir.

• Güç tasarrufu sağlanır.

• Yüksek güç sinyali iletilebilir.

• Daha az gürültü var.

• Sinyal solmasının meydana gelmesi daha az olasıdır.

Dezavantajları

• SSBSC dalgasının oluşumu ve tespiti karmaşık bir süreçtir.

• SSB vericisi ve alıcısı mükemmel bir frekans kararlılığına sahip olmadıkça sinyalin kalitesi etkilenir.

Uygulamalar

• Güç tasarrufu gereksinimleri ve düşük bant genişliği gereksinimleri için.

• Kara, hava ve denizcilik mobil iletişiminde.

• Noktadan noktaya iletişimde.

• Radyo iletişiminde.

• Televizyonda, telemetri ve radar iletişiminde.

• Amatör radyo vb. Askeri iletişimde.

Bu bölümde, SSBSC dalgasını oluşturan modülatörlerden bahsedelim. Aşağıdaki iki yöntemi kullanarak SSBSC dalgası oluşturabiliriz.

• Frekans ayrımcılık yöntemi
• Faz ayrımcılık yöntemi

Frekans Ayrımcılık Yöntemi

Aşağıdaki şekil, frekans ayrım yöntemini kullanan SSBSC modülatörünün blok diyagramını göstermektedir.

Bu yöntemde ilk olarak ürün modülatörü yardımıyla DSBSC dalgası oluşturacağız. Ardından, bu DSBSC dalgasını bir bant geçiren filtre girişi olarak uygulayın. Bu bant geçiş filtresi, SSBSC dalgası olan bir çıktı üretir.

İstenen SSBSC dalgasının spektrumu olarak bant geçiş filtresinin frekans aralığını seçin. Bu, bant geçiş filtresinin, üst yan banda veya alt yan banda sahip ilgili SSBSC dalgasını elde etmek için üst yan bant veya alt yan bant frekanslarına ayarlanabileceği anlamına gelir.

Faz Ayrımcılık Yöntemi

Aşağıdaki şekil, faz ayırma yöntemini kullanan SSBSC modülatörünün blok diyagramını göstermektedir.

Bu blok diyagram iki ürün modülatöründen, iki $ -90 ^ 0 $ faz kaydırıcıdan, bir yerel osilatörden ve bir yaz bloğundan oluşur. Ürün modülatörü, iki girişin ürünü olan bir çıktı üretir. $ -90 ^ 0 $ faz kaydırıcı, girdiye göre faz gecikmesi $ -90 ^ 0 $ olan bir çıktı üretir.

Yerel osilatör, taşıyıcı sinyali üretmek için kullanılır. Yaz bloğu, iki girişin toplamı veya girişlerin polaritesine bağlı olarak iki girişin farkı olan bir çıktı üretir.

$ A_m \ cos \ left (2 \ pi f_mt \ right) $ modülasyon sinyali ve $ A_c \ cos \ left (2 \ pi f_ct \ right) $, üst çarpım modülatörüne girişler olarak doğrudan uygulanır. Böylece, üst ürün modülatörü bu iki girdinin ürünü olan bir çıktı üretir.

Üst ürün modülatörünün çıktısı

$$ s_1 \ left (t \ sağ) = A_mA_c \ cos \ left (2 \ pi f_mt \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$

$$ \ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] + \ cos \ sol [2 \ pi \ sol (f_c-f_m \ sağ) t \ sağ] \ sağ \} $$

$ A_m \ cos \ left (2 \ pi f_mt \ right) $ modülasyon sinyali ve $ A_c \ cos \ left (2 \ pi f_ct \ right) $, aşağıdaki gibi uygulanmadan önce $ -90 ^ 0 $ ile faz kaydırılır. alt ürün modülatörüne girişler. Dolayısıyla, alt çarpım modülatörü, bu iki girdinin ürünü olan bir çıktı üretir.

Alt ürün modülatörünün çıktısı

$$ s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right) $$

$ \ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right) $

$ \ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] \ sağ \} $

$ S_1 \ left (t \ right) $ ve $ s_2 \ left (t \ right) $ ekleyerek SSBSC modülasyonlu $ s \ left (t \ right) $ dalgasının daha düşük bir yan banda sahip olmasını sağlayın.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] + \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] \ sağ \} + $

$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] - \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] \ sağ \} $

$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $

$ S_2 \ left (t \ right) $ 'ı $ s_1 \ left (t \ right) $' dan çıkarın ve SSBSC ile modüle edilmiş $ s \ left (t \ right) $ dalgasının üst kenar banda sahip olmasını sağlayın.

$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] + \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] \ sağ \} - $

$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] - \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] \ sağ \} $

$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] $

Bu nedenle, yaz bloğundaki girişlerin kutuplarını doğru bir şekilde seçerek, bir üst yan banda veya bir alt yan banda sahip olan SSBSC dalgasını elde edeceğiz.

SSBSC dalgasından orijinal bir mesaj sinyali çıkarma işlemi, SSBSC'nin tespiti veya demodülasyonu olarak bilinir. Tutarlı dedektör, SSBSC dalgasını demodüle etmek için kullanılır.

Tutarlı Dedektör

Burada, mesaj sinyalini tespit etmek için aynı taşıyıcı sinyal (SSBSC dalgası oluşturmak için kullanılır) kullanılır. Bu nedenle, bu tespit sürecinecoherent veya synchronous detection. Tutarlı dedektörün blok şeması aşağıdadır.

Bu süreçte mesaj sinyali SSBSC dalgasından aynı frekansa ve SSBSC modülasyonunda kullanılan taşıyıcının fazına sahip bir taşıyıcıyla çarpılarak çıkarılabilir. Ortaya çıkan sinyal daha sonra bir Düşük Geçiş Filtresinden geçirilir. Bu filtrenin çıktısı istenen mesaj sinyalidir.

Aşağıdakileri göz önünde bulundur SSBSC sahip dalga lower sideband.

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $$

Yerel osilatörün çıkışı

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Şekilden ürün modülatörünün çıktısını şöyle yazabiliriz:

$$ v \ left (t \ sağ) = s \ sol (t \ sağ) c \ sol (t \ sağ) $$

$ S \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini yukarıdaki denklemde değiştirin.

$$ v \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] A_c \ cos \ left (2 \ pi f_ct \ right) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ sağ) t \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ sağ) t \ sağ \} $

$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ sağ) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ sağ) t \ sağ] $

Yukarıdaki denklemde, ilk terim, mesaj sinyalinin ölçekli versiyonudur. Yukarıdaki sinyali bir düşük geçiş filtresinden geçirerek çıkarılabilir.

Bu nedenle, alçak geçiren filtrenin çıkışı

$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$

Burada ölçekleme faktörü $ \ frac {{A_ {c}} ^ {2}} {4} $ 'dır.

Üst yan banda sahip olan SSBSC dalgasını demodüle etmek için aynı blok diyagramı kullanabiliriz. Aşağıdakileri göz önünde bulundurSSBSC sahip dalga upper sideband.

$$ s \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] $$

Yerel osilatörün çıkışı

$$ c \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) $$

Ürün modülatörünün çıktısını şu şekilde yazabiliriz:

$$ v \ left (t \ sağ) = s \ sol (t \ sağ) c \ sol (t \ sağ) $$

$ S \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini yukarıdaki denklemde değiştirin.

$$ \ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$

$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ sağ) t \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $

$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ sağ) \ sağ \} $

$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ sağ) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ sağ) t \ sağ] $

Yukarıdaki denklemde, ilk terim, mesaj sinyalinin ölçekli versiyonudur. Yukarıdaki sinyali bir düşük geçiş filtresinden geçirerek çıkarılabilir.

Bu nedenle, düşük geçiş filtresinin çıkışı

$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$

Burada da ölçeklendirme faktörü $ \ frac {{A_ {c}} ^ {2}} {4} $ 'dır.

Bu nedenle, tutarlı detektör kullanarak her iki durumda da aynı demodüle çıktı elde ederiz.

Önceki bölümlerde, SSBSC modülasyonunu ve demodülasyonunu tartışmıştık. SSBSC ile modüle edilmiş sinyalin yalnızca bir yan bant frekansı vardır. Teorik olarak, ideal bir bant geçiren filtre kullanarak bir yan bant frekans bileşenini tamamen elde edebiliriz. Bununla birlikte, pratik olarak tüm yan bant frekansı bileşenini alamayabiliriz. Bundan dolayı bazı bilgiler kaybolur.

Bu kaybı önlemek için, DSBSC ve SSBSC arasında bir uzlaşma olan bir teknik seçilir. Bu teknik olarak bilinirVestigial Side Band Suppressed Carrier (VSBSC)tekniği. "Vestige" kelimesi, adın türetildiği "bir parça" anlamına gelir.

VSBSC ModulationVestige adı verilen sinyalin bir kısmının bir yan bant ile birlikte modüle edildiği süreçtir. VSBSC dalgasının frekans spektrumu aşağıdaki şekilde gösterilmiştir.

Bu teknikte üst yan bandın yanı sıra alt yan bandın bir kısmı da iletilmektedir. Benzer şekilde, alt yan bandı üst yan bandın bir parçasıyla birlikte iletebiliriz. Parazitleri önlemek için VSB'nin her iki tarafına çok küçük genişlikte bir koruma bandı döşenmiştir. VSB modülasyonu çoğunlukla televizyon yayınlarında kullanılır.

VSBSC Modülasyonunun Bant Genişliği

SSBSC ile modüle edilmiş dalganın bant genişliğinin $ f_m $ olduğunu biliyoruz. VSBSC ile modüle edilmiş dalga, bir yan bandın frekans bileşenlerini diğer yan bandın kalıntılarıyla birlikte içerdiğinden, bunun bant genişliği, SSBSC ile modüle edilmiş dalga ve vestige frekansının $ f_v $ bant genişliğinin toplamı olacaktır.

i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$

Avantajlar

VSBSC modülasyonunun avantajları aşağıdadır.

• Yüksek verimli.

• AM ve DSBSC dalgalarına kıyasla bant genişliğinde azalma.

• Yüksek doğruluk gerekmediğinden filtre tasarımı kolaydır.

• Düşük frekans bileşenlerinin iletimi herhangi bir zorluk olmadan mümkündür.

• İyi faz özelliklerine sahiptir.

Dezavantajları

VSBSC modülasyonunun dezavantajları aşağıdadır.

• Bant genişliği, SSBSC dalgasına kıyasla daha fazladır.

• Demodülasyon karmaşıktır.

Uygulamalar

VSBSC'nin en belirgin ve standart uygulaması televizyon sinyallerinin iletimi içindir. Ayrıca, bant genişliği kullanımı düşünüldüğünde bu en uygun ve verimli tekniktir.

Şimdi VSBSC dalgasını oluşturan modülatör ve VSBSC dalgasını tek tek demodüle eden demodülatör hakkında konuşalım.

VSBSC'nin oluşturulması

VSBSC dalgasının oluşumu, SSBSC dalgasının oluşumuna benzer. VSBSC modülatörü aşağıdaki şekilde gösterilmektedir.

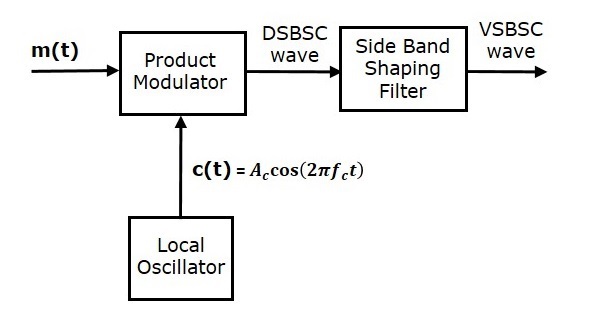
Bu yöntemde ilk olarak ürün modülatörü yardımıyla DSBSC dalgası oluşturacağız. Ardından, bu DSBSC dalgasını yan bant şekillendirme filtresinin bir girişi olarak uygulayın. Bu filtre, VSBSC dalgası olan bir çıktı üretir.

$ M \ left (t \ right) $ modülasyon sinyali ve $ A_c \ cos \ left (2 \ pi f_ct \ right) $ taşıyıcı sinyali, ürün modülatörüne girişler olarak uygulanır. Dolayısıyla, ürün modülatörü bu iki girdinin ürünü olan bir çıktı üretir.

Bu nedenle, ürün modülatörünün çıktısı

$$ p \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) m \ left (t \ sağ) $$

Her iki tarafa da Fourier dönüşümü uygulayın

$$ P \ left (f \ sağ) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ sağ) + M \ left (f + f_c \ sağ) \ sağ] $$

Yukarıdaki denklem DSBSC frekans spektrumunun denklemini temsil eder.

Yan bant şekillendirme filtresinin aktarım işlevi $ H \ left (f \ right) $ olsun. Bu filtre $ p \ left (t \ right) $ girdisine sahiptir ve çıktı VSBSC ile modüle edilmiş $ s \ left (t \ right) $ dalgasıdır. $ P \ left (t \ right) $ ve $ s \ left (t \ right) $ için Fourier dönüşümleri sırasıyla $ P \ left (t \ right) $ ve $ S \ left (t \ right) $ 'dır.

Matematiksel olarak $ S \ left (f \ right) $ şöyle yazabiliriz:

$$ S \ sol (t \ sağ) = P \ sol (f \ sağ) H \ sol (f \ sağ) $$

Yukarıdaki denklemde $ P \ left (f \ right) $ değerini değiştirin.

$$ S \ left (f \ sağ) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ sağ) + M \ left (f + f_c \ sağ) \ sağ] H \ sol ( f \ right) $$

Yukarıdaki denklem VSBSC frekans spektrumunun denklemini temsil eder.

VSBSC'nin demodülasyonu

VSBSC dalgasının demodülasyonu, SSBSC dalgasının demodülasyonuna benzer. Burada, mesaj sinyalini tespit etmek için (VSBSC dalgası oluşturmak için kullanılan) aynı taşıyıcı sinyal kullanılır. Bu nedenle, bu tespit sürecinecoherent veya synchronous detection. VSBSC demodülatör aşağıdaki şekilde gösterilmektedir.

Bu süreçte mesaj sinyali, VSBSC modülasyonunda kullanılan taşıyıcının aynı frekansa ve fazına sahip olan bir taşıyıcıyla çarpılarak VSBSC dalgasından çıkarılabilir. Ortaya çıkan sinyal daha sonra bir Düşük Geçiş Filtresinden geçirilir. Bu filtrenin çıktısı istenen mesaj sinyalidir.

VSBSC dalgası $ s \ left (t \ right) $ ve taşıyıcı sinyali $ A_c \ cos \ left (2 \ pi f_ct \ right) $ olsun.

Şekilden ürün modülatörünün çıktısını şu şekilde yazabiliriz:

$$ v \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) s \ left (t \ sağ) $$

Her iki tarafa da Fourier dönüşümü uygulayın

$$ V \ left (f \ sağ) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ sağ) + S \ left (f + f_c \ sağ) \ sağ] $$

Bunu biliyoruz $ S \ (sağ f \) sol = \ frac {A_C} {2} \ sol [M \ sol (f F_C \ sağ) + M \ sol (f + F_C \ sağ) \ doğru] H \ sol (f \ sağ) $

Yukarıdaki denklemden $ S \ left (f-f_c \ right) $ ve $ S \ left (f + f_c \ right) $ bulalım.

$$ S \ left (f-f_c \ sağ) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ sağ) + M \ left (f-f_c + f_c \ sağ) \ sağ] H \ sol (f-f_c \ sağ) $$

$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ sağ) + M \ left (f \ sağ) \ sağ] H \ sol (f-f_c \ sağ) $

$$ S \ left (f + f_c \ sağ) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ sağ) + M \ left (f + f_c + f_c \ sağ) \ sağ] H \ sol (f + f_c \ sağ) $$

$ \ Rightarrow S \ left (f + f_c \ sağ) = \ frac {A_c} {2} \ left [M \ left (f \ sağ) + M \ left (f + 2f_c \ sağ) \ sağ] H \ sol (f + f_c \ sağ) $

$ V \ left (f \ right) $ içindeki $ S \ left (f-f_c \ right) $ ve $ S \ left (f + f_c \ right) $ değerlerini değiştirin.

$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $

$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $

$ \ Rightarrow V \ left (f \ sağ) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ sağ) \ left [H \ left (f-f_c \ sağ) + H \ left (f + f_c \ sağ) \ sağ] $

$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ sağ) H \ left (f-f_c \ sağ) + M \ left (f + 2f_c \ sağ) H \ sol (f + f_c \ sağ) \ sağ] $

Yukarıdaki denklemde, birinci terim, istenen mesaj sinyali frekans spektrumunun ölçekli versiyonunu temsil eder. Yukarıdaki sinyali düşük geçişli bir filtreden geçirerek çıkarılabilir.

$$ V_0 \ left (f \ sağ) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ sağ) \ left [H \ left (f-f_c \ sağ) + H \ left (f + f_c \ sağ) \ sağ] $$

Sürekli dalga modülasyonunda diğer modülasyon türü Angle Modulation. Açı Modülasyonu, taşıyıcı sinyalin frekansının veya fazının mesaj sinyaline göre değiştiği süreçtir.

Açı modülasyonlu dalganın standart denklemi

$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$

Nerede,

$ A_c $, taşıyıcı sinyalin genliği ile aynı olan modüle edilmiş dalganın genliğidir

$ \ theta _i \ left (t \ right) $, modüle edilmiş dalganın açısıdır

Açı modülasyonu ayrıca frekans modülasyonu ve faz modülasyonu olarak ikiye ayrılır.

• Frequency Modulation taşıyıcı sinyalin frekansının mesaj sinyali ile doğrusal olarak değiştirilmesi işlemidir.

• Phase Modulation taşıyıcı sinyalin fazını mesaj sinyali ile doğrusal olarak değiştirme işlemidir.

Şimdi bunları detaylı olarak tartışalım.

Frekans modülasyonu

Genlik modülasyonunda, taşıyıcı sinyalin genliği değişir. OysaFrequency Modulation (FM)taşıyıcı sinyalin frekansı, modüle edici sinyalin anlık genliğine göre değişir.

Bu nedenle, frekans modülasyonunda, taşıyıcı sinyalin genliği ve fazı sabit kalır. Aşağıdaki şekillere bakılarak bu daha iyi anlaşılabilir.

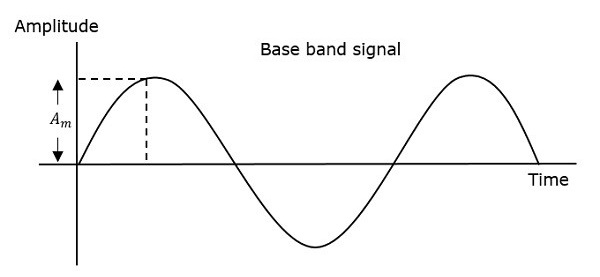
Modüle edilen dalganın frekansı, modülasyon veya mesaj sinyalinin genliği arttığında artar. Benzer şekilde, modüle edilen dalganın frekansı, modüle edici sinyalin genliği azaldığında azalır. Modüle edilen dalganın frekansının sabit kaldığına ve modüle edici sinyalin genliği sıfır olduğunda taşıyıcı sinyalin frekansına eşit olduğuna dikkat edin.

Matematiksel Gösterim

FM modülasyonunda anlık frekans $ f_i $ için denklem şu şekildedir:

$$ f_i = f_c + k_fm \ left (t \ sağ) $$

Nerede,

$ f_c $ taşıyıcı frekansıdır

$ k_t $ frekans duyarlılığıdır

$ m \ left (t \ right) $ mesaj sinyalidir

$ \ Omega_i $ açısal frekansı ile $ \ theta _i \ left (t \ right) $ açısı arasındaki ilişkiyi biliyoruz.

$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$

$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $

Yukarıdaki denklemde $ f_i $ değerini değiştirin.

$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ sağ) \ sağ) dt $$

$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $

Açı modülasyonlu dalganın standart denkleminde $ \ theta _i \ left (t \ right) $ değerini değiştirin.

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ) $$

Bu equation of FM wave.

Modülasyon sinyali $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $ ise, FM dalgasının denklemi

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ sağ) \ sağ) $$

Nerede,

$ \ beta $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $

FM modülasyonlu frekans (anlık frekans) ile normal taşıyıcı frekansı arasındaki fark şu şekilde adlandırılır: Frequency Deviation. $ K_f $ ve $ A_m $ değerlerinin çarpımına eşit olan $ \ Delta f $ ile gösterilir.

FM ayrılabilir Narrowband FM ve Wideband FM $ \ beta $ modülasyon endeksinin değerlerine göre.

Dar bant FM

Aşağıda Narrowband FM'in özellikleri verilmiştir.

• Bu frekans modülasyonu, geniş bant FM ile karşılaştırıldığında küçük bir bant genişliğine sahiptir.

• $ \ Beta $ modülasyon endeksi küçüktür, yani 1'den küçüktür.

• Yelpazesi taşıyıcı, üst yan bant ve alt yan banttan oluşur.

• Bu, polis telsizi, ambulanslar, taksiler gibi mobil iletişimlerde kullanılır.

Geniş bant FM

Aşağıda Geniş Bant FM'in özellikleri yer almaktadır.

• Bu frekans modülasyonunun sonsuz bant genişliği vardır.

• $ \ Beta $ modülasyon endeksi büyük, yani 1'den büyük.

• Spektrumu, bir taşıyıcı ve etrafına yerleştirilmiş sonsuz sayıda yan banttan oluşur.

• Bu, eğlence, FM radyo, TV vb. Yayın uygulamalarında kullanılır.

Faz Modülasyonu

Frekans modülasyonunda, taşıyıcının frekansı değişir. OysaPhase Modulation (PM)Taşıyıcı sinyalin fazı, modüle edici sinyalin anlık genliğine göre değişir.

Dolayısıyla, faz modülasyonunda, taşıyıcı sinyalin genliği ve frekansı sabit kalır. Aşağıdaki şekillere bakılarak bu daha iyi anlaşılabilir.

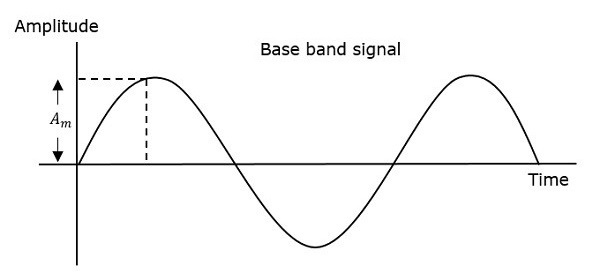
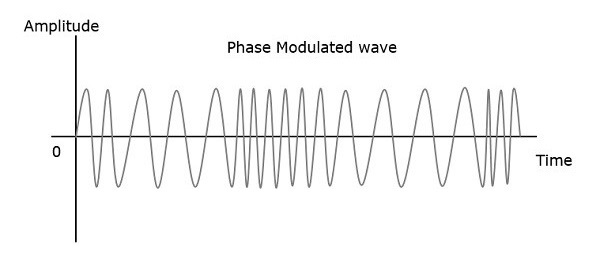
Modüle edilmiş dalganın fazı, bir dalgadaki faz kaymasının gerçekleşebileceği sonsuz noktalara sahiptir. Modüle edici sinyalin anlık genliği, taşıyıcı sinyalin fazını değiştirir. Genlik pozitif olduğunda, faz bir yönde değişir ve genlik negatif ise faz ters yönde değişir.

Matematiksel Gösterim

Faz modülasyonunda anlık faz $ \ phi_i $ için denklem şu şekildedir:

$$ \ phi _i = k_p m \ left (t \ right) $$

Nerede,

• $ k_p $, faz duyarlılığıdır

• $ m \ left (t \ right) $ mesaj sinyalidir

Açı modülasyonlu dalganın standart denklemi

$$ s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$

Yukarıdaki denklemde $ \ phi_i $ değerini değiştirin.

$$ s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ sağ) \ sağ) $$

Bu equation of PM wave.

Modülasyon sinyali, $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $ ise, PM dalgasının denklemi

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ sağ) \ sağ) $$

Nerede,

• $ \ beta $ = modulation index = $ \ Delta \ phi = k_pA_m $

• $ \ Delta \ phi $ faz sapmasıdır

Faz modülasyonu mobil iletişim sistemlerinde kullanılırken, frekans modülasyonu esas olarak FM yayını için kullanılır.

Önceki bölümde, Açı modülasyonunda kullanılan parametreleri tartışmıştık. Her parametrenin kendi formülü vardır. Bu formülleri kullanarak, ilgili parametre değerlerini bulabiliriz. Bu bölümde, Frekans Modülasyonu kavramına dayalı olarak birkaç sorunu çözelim.

Problem 1

Frekans duyarlılığı 40 Hz / volt olan FM jeneratörüne, 5 V genlikli sinüzoidal modüle edici dalga formu ve 2 KHz frekans uygulanır. Frekans sapmasını, modülasyon indeksini ve bant genişliğini hesaplayın.

Çözüm

Verilen, modüle edici sinyalin genliği, $ A_m = 5V $

Modülasyon sinyalinin frekansı, $ f_m = 2 KHz $

Frekans hassasiyeti, $ k_f = 40 Hz / volt $

Frekans sapmasının formülünü şu şekilde biliyoruz:

$$ \ Delta f = k_f A_m $$

Yukarıdaki formülde $ k_f $ ve $ A_m $ değerlerini değiştirin.

$$ \ Delta f = 40 \ times 5 = 200Hz $$

Bu nedenle, frequency deviation$ \ Delta f $, 200Hz $ 'dır

Modülasyon indeksi formülü şöyledir:

$$ \ beta = \ frac {\ Delta f} {f_m} $$

Yukarıdaki formülde $ \ Delta f $ ve $ f_m $ değerlerini değiştirin.

$$ \ beta = \ frac {200} {2 \ times 1000} = 0,1 $$

İşte değeri modulation index$ \ beta $, 0.1'den küçüktür. Dolayısıyla Dar Bant FM'dir.

Dar Bant FM'in Bant Genişliği formülü, AM dalgası ile aynıdır.

$$ BW = 2f_m $$

Yukarıdaki formülde $ f_m $ değerini değiştirin.

$$ BW = 2 \ times 2K = 4KHz $$

bu yüzden bandwidth Dar Bant FM dalgası 4 KHz $ 'dır.

Problem 2

Bir FM dalgası $ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right ile verilir ) $. FM dalgasının frekans sapmasını, bant genişliğini ve gücünü hesaplayın.

Çözüm

Verildiğinde, bir FM dalgasının denklemi

$$ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ sağ) $$

Bir FM dalgasının standart denklemini şu şekilde biliyoruz:

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ sağ) \ sağ) $$

Yukarıdaki iki denklemi karşılaştırarak aşağıdaki değerleri elde edeceğiz.

Taşıyıcı sinyalin genliği, $ A_c = 20V $

Taşıyıcı sinyalin frekansı, $ f_c = 4 \ times 10 ^ 6 Hz = 4 MHz $

Mesaj sinyalinin frekansı, $ f_m = 1 \ times 10 ^ 3 Hz = 1KHz $

Modülasyon endeksi, $ \ beta = 9 $

Burada modülasyon indeksinin değeri birden büyüktür. Bu nedenleWide Band FM.

Modülasyon indeksi formülünü şu şekilde biliyoruz:

$$ \ beta = \ frac {\ Delta f} {f_m} $$

Yukarıdaki denklemi aşağıdaki gibi yeniden düzenleyin.

$$ \ Delta = \ beta f_m $$

Yukarıdaki denklemde $ \ beta $ ve $ f_m $ değerlerini değiştirin.

$$ \ Delta = 9 \ times 1K = 9 KHz $$

Bu nedenle, frequency deviation$ \ Delta f $, 9 $ KHz $ 'dır.

Geniş Bant FM dalgasının Bant Genişliği formülü

$$ BW = 2 \ left (\ beta +1 \ sağ) f_m $$

Yukarıdaki formülde $ \ beta $ ve $ f_m $ değerlerini değiştirin.

$$ BW = 2 \ sol (9 +1 \ sağ) 1K = 20KHz $$

bu yüzden bandwidth Geniş Bant FM dalgası 20 KHz $

FM dalgasının gücü için formül

$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$

$ R = 1 \ Omega $ varsayalım ve yukarıdaki denklemde $ A_c $ değerini değiştirelim.

$$ P = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200 W $$

bu yüzden power FM dalgasının yüzdesi 200 $ watts.

Bu bölümde, NBFM ve WBFM dalgalarını oluşturan modülatörler hakkında tartışalım. Öncelikle, NBFM'nin oluşumunu tartışalım.

NBFM üretimi

FM dalgasının standart denkleminin olduğunu biliyoruz

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ sağ) - $

$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ) $

NBFM için,

$$ \ left | 2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ | <<1 $$

$ \ Theta $ çok küçük olduğunda $ \ cos \ theta \ yaklaşık 1 $ ve $ \ sin \ theta \ yaklaşık 1 $ olduğunu biliyoruz.

Yukarıdaki ilişkileri kullanarak, NBFM equation gibi

$$ s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) -A_c \ sin \ left (2 \ pi f_ct \ sağ) 2 \ pi k_f \ int m \ left (t \ sağ) dt $$

NBFM modülatörünün blok şeması aşağıdaki şekilde gösterilmektedir.

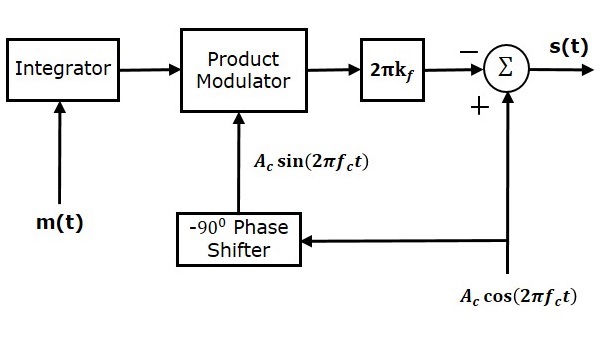
Burada, entegratör $ m \ left (t \ right) $ modülasyon sinyalini entegre etmek için kullanılır. Taşıyıcı sinyali $ A_c \ cos \ left (2 \ pi f_ct \ right) $, $ A_c \ sin \ left (2 \ pi f_ct \ right) $ almak için $ -90 ^ 0 $ ile kaydırılan fazdır $ -90 ^ 0 $ faz kaydırıcı. Ürün modülatörünün iki $ \ int m \ left (t \ right) dt $ ve $ A_c \ sin \ left (2 \ pi f_ct \ right) $ girdisi vardır. Bu iki girdinin ürünü olan bir çıktı üretir.

Bu, ileri yola bir $ 2 \ pi k_f $ bloğu yerleştirerek $ 2 \ pi k_f $ ile çarpılır. Yaz bloğunun, NBFM denkleminin iki teriminden başka bir şey olmayan iki girişi vardır. Taşıyıcı sinyal için pozitif ve negatif işaretler ve yaz bloğunun girişindeki diğer terim atanır. Son olarak, yaz bloğu NBFM dalgası üretir.

WBFM'nin oluşturulması

Aşağıdaki iki yöntem WBFM dalgası oluşturur.

• Direkt yöntem
• Dolaylı yöntem

Direkt yöntem

Bu yönteme Doğrudan Yöntem deniyor çünkü doğrudan geniş bantlı bir FM dalgası oluşturuyoruz. Bu yöntemde, WBFM oluşturmak için Voltaj Kontrollü Osilatör (VCO) kullanılır. VCO, frekansı giriş sinyali voltajıyla orantılı olan bir çıkış sinyali üretir. Bu, FM dalgasının tanımına benzer. WBFM dalgasının oluşumunun blok diyagramı aşağıdaki şekilde gösterilmektedir.

Burada, $ m \ left (t \ right) $ modülasyon sinyali, Voltaj Kontrollü Osilatörün (VCO) girişi olarak uygulanır. VCO, WBFM'den başka bir şey olmayan bir çıktı üretir.

$$ f_i \: \ alpha \: m \ left (t \ right) $$

$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ sağ) $$

Nerede,

$ f_i $, WBFM dalgasının anlık frekansıdır.

Dolaylı Yöntem

Dolaylı olarak geniş bant FM dalgası oluşturduğumuz için bu yönteme Dolaylı Yöntem denir. Bu, önce NBFM dalgası oluşturacağımız ve ardından frekans çarpanları yardımıyla WBFM dalgasını alacağımız anlamına gelir. WBFM dalgası oluşumunun blok diyagramı aşağıdaki şekilde gösterilmiştir.

Bu blok diyagram esas olarak iki aşama içerir. İlk aşamada, NBFM dalgası NBFM modülatörü kullanılarak üretilecektir. Bu bölümün başında NBFM modülatörünün blok diyagramını gördük. NBFM dalgasının modülasyon indeksinin birden az olduğunu biliyoruz. Bu nedenle, FM dalgasının gerekli modülasyon indeksini (birden fazla) elde etmek için frekans çarpanı değerini doğru seçin.

Frequency multiplierdoğrusal olmayan bir cihazdır ve frekansı giriş sinyali frekansının 'n' katı olan bir çıkış sinyali üretir. Burada 'n' çarpım faktörüdür.

Modülasyon indeksi $ \ beta $ 1'den küçük olan NBFM dalgası frekans çarpanı girdisi olarak uygulanırsa, frekans çarpanı modülasyon indeksi 'n' çarpı $ \ beta $ ve frekansı da 'n olan bir çıkış sinyali üretir. WBFM dalgasının frekansının katı.

Bazen, FM dalgasının frekans sapmasını ve modülasyon indeksini artırmak için birden fazla frekans çarpanı ve karıştırıcı aşamasına ihtiyaç duyabiliriz.

Bu bölümde FM dalgasını demodüle eden demodülatörler hakkında konuşalım. Aşağıdaki iki yöntem FM dalgasını demodüle eder.

• Frekans ayrımcılık yöntemi
• Faz ayrımcılık yöntemi

Frekans Ayrımcılık Yöntemi

FM dalgasının denkleminin şöyle olduğunu biliyoruz

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ) $$

Yukarıdaki denklemi 't'.

$$ \ frac {ds \ left (t \ right)} {dt} = -A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ sağ) \ sağ) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ sağ) dt \ sağ) $$

$ - \ sin \ theta $ 'ı $ \ sin \ left (\ theta -180 ^ 0 \ right) $ olarak yazabiliriz.

$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ sağ) dt-180 ^ 0 \ sağ) $$

$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c \ right) \ left [1+ \ left (\ frac {k_f} {k_c} \ sağ) m \ sol ( t \ right) \ right] \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ sağ) $$

Yukarıdaki denklemde genlik terimi AM dalgasının zarfını andırır ve açı terimi FM dalgasının açısını andırır. Buradaki gereksinimimiz $ m \ left (t \ right) $ modülasyon sinyalidir. Bu nedenle, onu AM dalgasının zarfından kurtarabiliriz.

Aşağıdaki şekil, frekans ayırt etme yöntemini kullanan FM demodülatörünün blok şemasını göstermektedir.

Bu blok diyagram, farklılaştırıcı ve zarf detektöründen oluşur. Farklılaştırıcı, FM dalgasını AM dalgası ve FM dalgasının bir kombinasyonuna dönüştürmek için kullanılır. Bu, FM dalgasının frekans değişimlerini, AM dalgasının karşılık gelen voltaj (genlik) varyasyonlarına dönüştürdüğü anlamına gelir. Zarf detektörünün işleyişini biliyoruz. Modülasyon sinyalinden başka bir şey olmayan AM dalgasının demodüle edilmiş çıkışını üretir.

Faz Ayrımcılık Yöntemi

Aşağıdaki şekil, faz ayırma yöntemini kullanan FM demodülatörünün blok diyagramını göstermektedir.

Bu blok diyagram çarpan, alçak geçiren filtre ve Voltaj Kontrollü Osilatörden (VCO) oluşur. VCO, frekansı $ d \ left (t \ right) $ giriş sinyali voltajıyla orantılı olan bir $ v \ left (t \ right) $ çıkış sinyali üretir. Başlangıçta, $ d \ left (t \ right) $ sinyali sıfır olduğunda, taşıyıcı frekansı ve $ -90 ^ 0 $ faz kayması olan $ v \ left (t \ right) $ çıkış sinyali üretmek için VCO'yu ayarlayın. taşıyıcı sinyale göre.

FM dalgası $ s \ left (t \ right) $ ve VCO çıkışı $ v \ left (t \ right) $ çarpanın girdileri olarak uygulanır. Çarpan, bir yüksek frekans bileşenine ve bir düşük frekans bileşenine sahip bir çıktı üretir. Düşük geçiş filtresi, yüksek frekans bileşenini ortadan kaldırır ve yalnızca düşük frekans bileşenini çıktı olarak üretir.

Bu düşük frekans bileşeni yalnızca terimle ilgili faz farkını içerir. Bu nedenle, düşük geçiş filtresinin bu çıkışından $ m \ left (t \ right) $ modülasyon sinyalini alıyoruz.

Multiplexingbirden fazla sinyali ortak bir ortam üzerinden tek bir sinyalde birleştirme işlemidir. Analog sinyaller çoklanmışsa, o zamananalog multiplexing. Benzer şekilde, dijital sinyaller çoklanmışsa, o zamandigital multiplexing.

Çoğullama ilk olarak telefonda geliştirildi. Tek bir kablo üzerinden göndermek için bir dizi sinyal birleştirildi. Çoklama işlemi, bir iletişim kanalını birkaç mantıksal kanala böler, her birini farklı bir mesaj sinyali veya aktarılacak bir veri akışı için tahsis eder. Çoklama yapan cihaz şu şekilde çağrılabilir:Multiplexer veya MUX.

Alıcıda yapılan ters işlem, yani bir kanaldan kanal sayısının çıkarılması, de-multiplexing. Çoğullama çözen cihaz şu şekilde çağrılabilir:de-multiplexer veya DEMUX.

Aşağıdaki şekiller MUX ve DEMUX konseptini göstermektedir. Birincil kullanımları iletişim alanındadır.

Çoklayıcı Türleri

Analog ve dijital olmak üzere başlıca iki tür çoklayıcı vardır. Ayrıca, Frekans Bölmeli Çoklama (FDM), Dalgaboyu Bölmeli Çoklama (WDM) ve Zaman Bölmeli Çoklama (TDM) olarak ikiye ayrılırlar. Aşağıdaki şekil bu sınıflandırma hakkında ayrıntılı bir fikir vermektedir.

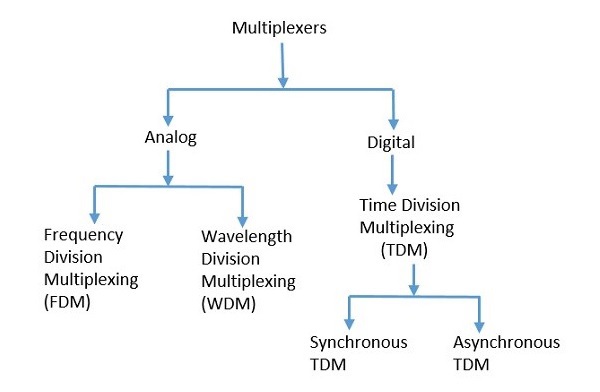
Pek çok tür çoğullama tekniği vardır. Bunların dışında, yukarıdaki şekilde belirtilen genel sınıflandırmaya sahip ana türlere sahibiz. Onlara ayrı ayrı bakalım.

Analog Çoklama

Analog çoklama tekniklerinde kullanılan sinyaller doğası gereği analogdur. Analog sinyaller, frekanslarına (FDM) veya dalga boylarına (WDM) göre çoklanır.

Frekans Bölmeli Çoğullama

Analog çoğullamada en çok kullanılan teknik, Frekans Bölmeli Çoğullamadır (FDM). Bu teknik, veri akışlarını tek bir sinyal olarak bir iletişim ortamında göndermek üzere birleştirmek için çeşitli frekanslar kullanır.

Example - Bir dizi kanalı tek bir kabloyla gönderen geleneksel bir televizyon vericisi FDM kullanır.

Dalgaboyu Bölmeli Çoğullama

Dalgaboyu Bölmeli çoğullama (WDM), ışık spektrumunda farklı dalga boylarındaki birçok veri akışının iletildiği analog bir tekniktir. Dalga boyu artarsa, sinyalin frekansı azalır. MUX çıkışında ve DEMUX girişinde farklı dalga boylarını tek bir hatta dönüştürebilen bir prizma kullanılabilir.

Example - Optik fiber iletişimler, farklı dalga boylarını iletişim için tek bir ışıkta birleştirmek için WDM tekniğini kullanır.

Dijital Çoklama

Dijital terimi, ayrık bilgi bitlerini temsil eder. Dolayısıyla, mevcut veriler, ayrık çerçeveler veya paketler şeklindedir.

Zaman Bölmeli Çoğullama

Zaman Bölmeli Çoğullamada (TDM), zaman çerçevesi yuvalara bölünmüştür. Bu teknik, her mesaj için bir dilim tahsis ederek tek bir iletişim kanalı üzerinden bir sinyali iletmek için kullanılır.

Zaman Bölmeli Çoklama (TDM), Senkronize TDM ve Asenkron TDM olarak sınıflandırılabilir.

Senkron TDM

Senkron TDM'de, giriş bir çerçeveye bağlanır. "N" sayıda bağlantı varsa, çerçeve "n" zaman dilimlerine bölünür. Her giriş satırı için bir yuva tahsis edilmiştir.

Bu teknikte, örnekleme hızı tüm sinyaller için ortaktır ve bu nedenle aynı saat girişi verilir. MUX,same slot her zaman her cihaza.

Eşzamansız TDM

Eşzamansız TDM'de, örnekleme hızı her sinyal için farklıdır ve ortak bir saat gerekli değildir. Bir zaman dilimi için ayrılan cihaz hiçbir şey iletmezse ve boşta kalırsa, o zaman bu yuvaallotted to another cihaz, senkrondan farklı olarak

Bu tür TDM, Eşzamansız aktarım modu ağlarında kullanılır.

De-Multiplexer

Çoklayıcı çözücüler, tek bir kaynağı birden çok hedefe bağlamak için kullanılır. Bu süreç, çoğullamanın tersi işlemidir. Daha önce de belirtildiği gibi, daha çok alıcılarda kullanılmaktadır. DEMUX'un birçok uygulaması vardır. Haberleşme sistemlerinde alıcılarda kullanılır. Bilgisayarlarda aritmetik ve mantıksal birimde güç sağlamak ve iletişimi iletmek vb.

Çoklayıcı çözücüler, seri-paralel dönüştürücüler olarak kullanılır. Seri veriler, düzenli aralıklarla DEMUX'a girdi olarak verilir ve çoğullayıcının çıkışını kontrol etmek için ona bir sayaç eklenir.

Hem çoklayıcılar hem de çoğullayıcılar, hem verici hem de alıcı bölümlerinde iletişim sistemlerinde önemli bir rol oynar.

Herhangi bir iletişim sisteminde, sinyalin iletimi sırasında veya sinyali alırken, bazı istenmeyen sinyaller iletişime girerek alıcı için rahatsız edici hale gelir ve iletişimin kalitesini sorgular. Böyle bir rahatsızlık denirNoise.

Gürültü nedir?

Gürültü bir unwanted signal, orijinal mesaj sinyaline müdahale eden ve mesaj sinyalinin parametrelerini bozan. İletişim sürecindeki bu değişiklik, mesajın değişmesine neden olur. Büyük olasılıkla kanala veya alıcıya girer.

Gürültü sinyali, aşağıdaki şekle bakılarak anlaşılabilir.

Bu nedenle, gürültünün hiçbir modeli ve sabit frekansı veya genliği olmayan bir sinyal olduğu anlaşılmaktadır. Oldukça rastgele ve tahmin edilemez. Tamamen ortadan kaldırılamasa da, genellikle onu azaltmak için önlemler alınır.

En yaygın gürültü örnekleri şunlardır:

• Radyo alıcılarında tıs sesi

• Telefon görüşmelerinin ortasında vızıltı sesi

• Televizyon alıcılarında vb. Titreme

Gürültü Türleri

Gürültünün sınıflandırılması, kaynağın türüne, gösterdiği etkiye veya alıcıyla olan ilişkisine vb. Göre yapılır.

Gürültünün üretilmesinin iki ana yolu vardır. Biri bazılarının içindenexternal source diğeri ise bir internal source, alıcı bölümünde.

Dış kaynak

Bu gürültü, genellikle iletişim ortamında veya kanalında meydana gelebilen dış kaynaklar tarafından üretilir. Bu gürültü tamamen ortadan kaldırılamaz. En iyi yol, gürültünün sinyali etkilemesini önlemektir.

Örnekler

Bu tür gürültünün en yaygın örnekleri şunlardır:

• Atmosferik gürültü (atmosferdeki düzensizlikler nedeniyle).

• Güneş gürültüsü ve kozmik gürültü gibi dünya dışı gürültü.

• Endüstriyel gürültü.

Dahili Kaynak

Bu gürültü, çalışırken alıcı bileşenleri tarafından üretilir. Sürekli çalışma nedeniyle devrelerdeki bileşenler az sayıda gürültü üretebilir. Bu gürültü ölçülebilir. Uygun bir alıcı tasarımı, bu dahili gürültünün etkisini azaltabilir.

Examples

Bu tür gürültünün en yaygın örnekleri şunlardır:

• Termal ajitasyon gürültüsü (Johnson gürültüsü veya Elektrik gürültüsü)

• Atış gürültüsü (elektronların ve deliklerin rastgele hareketinden dolayı)

• Geçiş süresi gürültüsü (geçiş sırasında)

• Çeşitli gürültü, titreme, direnç etkisi ve karıştırıcı tarafından oluşturulan gürültü vb. İçeren başka bir gürültü türüdür.

Gürültünün Etkileri

Gürültü, sistem performansını etkileyen uygunsuz bir özelliktir. Gürültünün etkileri aşağıdadır.

Gürültü, sistemlerin çalışma aralığını sınırlar

Gürültü dolaylı olarak en zayıf sinyale bir amplifikatör tarafından yükseltilebilecek bir sınır koyar. Karıştırıcı devresindeki osilatör, gürültü nedeniyle frekansını sınırlayabilir. Bir sistemin çalışması, devrelerinin çalışmasına bağlıdır. Gürültü, bir alıcının işleyebileceği en küçük sinyali sınırlar.

Gürültü alıcıların hassasiyetini etkiler

Hassasiyet, belirtilen kalitede çıktı elde etmek için gerekli minimum giriş sinyali miktarıdır. Gürültü, bir alıcı sistemin hassasiyetini etkiler ve sonuçta çıktıyı etkiler.

Bu bölümde, alıcıda demodüle edilen çeşitli modüle edilmiş dalgaların Sinyal-Gürültü Oranlarını ve Değer Şekillerini hesaplayalım.

Sinyal gürültü oranı

Signal-to-Noise Ratio (SNR)sinyal gücünün gürültü gücüne oranıdır. SNR değeri ne kadar yüksekse, alınan çıktının kalitesi de o kadar büyük olacaktır.

Farklı noktalardaki Sinyal-Gürültü Oranı aşağıdaki formüller kullanılarak hesaplanabilir.

Input SNR = $ \ left (SNR \ sağ) _I = \ frac {Ortalama \: \: güç \: \: / \: \: modülasyon \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: input} $

Output SNR = $ \ left (SNR \ sağ) _O = \ frac {Ortalama \: \: güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: çıktı} $

Channel SNR = $ \ left (SNR \ sağ) _C = \ frac {Ortalama \: \: güç \: \: / \: \: modüle edilmiş \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: mesaj \: \: bant genişliği} $

Liyakat Figürü

Çıkış SNR ve giriş SNR oranı şu şekilde adlandırılabilir: Figure of Merit. İle gösterilirF. Bir cihazın performansını açıklar.

$$ F = \ frac {\ sol (SNR \ sağ) _O} {\ sol (SNR \ sağ) _I} $$

Bir alıcının liyakat değeri

$$ F = \ frac {\ sol (SNR \ sağ) _O} {\ sol (SNR \ sağ) _C} $$

Bu böyledir çünkü bir alıcı için kanal giriştir.

AM Sisteminde SNR Hesaplamaları

Gürültüyü analiz etmek için aşağıdaki AM sisteminin alıcı modelini düşünün.

Genlik Modülasyonlu (AM) dalgasının

$$ s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$

$$ \ Rightarrow s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) + A_ck_am \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$

AM dalgasının ortalama gücü

$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $

$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$

Mesaj bant genişliğindeki ortalama gürültü gücü

$$ P_ {nc} = WN_0 $$

İkame, bu değerler channel SNR formül

$$ \ left (SNR \ sağ) _ {C, AM} = \ frac {Ortalama \: \: Güç \: \: / \: \: AM \: \: Dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ sağ) P } {2WN_0} $$

Nerede,

• P mesaj sinyalinin gücü = $ \ frac {{A_ {m}} ^ {2}} {2} $

• W mesaj bant genişliği

Yukarıdaki şekilde gösterildiği gibi bant geçiş gürültüsünün kanaldaki AM dalgasıyla karıştırıldığını varsayın. Bu kombinasyon, AM demodülatörünün girişine uygulanır. Bu nedenle, AM demodülatörünün girişi.

$$ v \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$

$ \ Rightarrow v \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ right) + $

$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ sağ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ] $

$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ sağ) + n_1 \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) $

$ N_I \ left (t \ right) $ ve $ n_Q \ left (t \ right) $, gürültünün faz ve kuadratür faz bileşenlerindeyken.

AM demodülatörünün çıkışı, yukarıdaki sinyalin zarfından başka bir şey değildir.

$$ d \ left (t \ sağ) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ sağ) \ sağ] ^ 2 + \ left (n_Q \ left (t \ sağ) \ sağ) ^ 2} $$

$$ \ Rightarrow d \ sol (t \ sağ) \ yaklaşık A_c + A_ck_am \ sol (t \ sağ) + n_1 \ sol (t \ sağ) $$

Demodüle edilmiş sinyalin ortalama gücü

$$ P_m = \ left (\ frac {A_ck_am \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$

Çıkıştaki ortalama gürültü gücü

$$ P_no = WN_0 $$

İkame, bu değerler output SNR formül.

$$ \ left (SNR \ sağ) _ {O, AM} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: Çıktı} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$

İkame, içindeki değerler Figure of merit AM alıcı formülü.

$$ F = \ frac {\ left (SNR \ sağ) _ {O, AM}} {\ left (SNR \ sağ) _ {C, AM}} $$

$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ sağ) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$

$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$

Bu nedenle, AM alıcısının liyakat figürü birden azdır.

DSBSC Sisteminde SNR Hesaplamaları

Gürültüyü analiz etmek için DSBSC sisteminin aşağıdaki alıcı modelini düşünün.

DSBSC modülasyonlu dalganın

$$ s \ left (t \ sağ) = A_cm \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$

DSBSC modülasyonlu dalganın ortalama gücü

$$ P_s = \ left (\ frac {A_cm \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$

Mesaj bant genişliğindeki ortalama gürültü gücü

$$ P_ {nc} = WN_0 $$

İkame, bu değerler channel SNR formül.

$$ \ left (SNR \ sağ) _ {C, DSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: DSBSC \: \: modüle edilmiş \: \: dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

Yukarıdaki şekilde gösterildiği gibi, bant geçiş gürültüsünün kanalda DSBSC ile modüle edilmiş dalga ile karıştırıldığını varsayın. Bu kombinasyon, ürün modülatörünün girdilerinden biri olarak uygulanır. Bu nedenle, bu ürün modülatörünün girişi

$$ v_1 \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$

$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ sağ) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ sağ) - n_Q \ sol (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ] $$

$$ \ Rightarrow v_1 \ left (t \ sağ) = \ sol [A_cm \ sol (t \ sağ) + n_I \ sol (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ sağ) $$

Yerel osilatör $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $ taşıyıcı sinyalini üretir. Bu sinyal, ürün modülatörüne başka bir giriş olarak uygulanır. Bu nedenle, ürün modülatörü $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ 'ın çarpımı olan bir çıktı üretir.

$$ v_2 \ sol (t \ sağ) = v_1 \ sol (t \ sağ) c \ sol (t \ sağ) $$

Yukarıdaki denklemde $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini değiştirin.

$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ] \ cos ^ 2 \ left (2 \ pi f_ct \ sağ ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ sağ) $$

$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ sağ)} {2} \ sağ) -n_Q \ sol (t \ sağ) \ frac {\ sin \ left (4 \ pi f_ct \ sağ)} {2} $$

Yukarıdaki sinyal alçak geçiren filtreye giriş olarak uygulandığında, alçak geçiren filtre çıktısını şu şekilde alacağız:

$$ d \ left (t \ sağ) = \ frac {\ left [A_c m \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ]} {2} $$

Demodüle edilmiş sinyalin ortalama gücü

$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$

Çıkıştaki ortalama gürültü gücü

$$ P_ {no} = \ frac {WN_0} {4} $$

İkame, bu değerler output SNR formül.

$$ \ left (SNR \ sağ) _ {O, DSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: Çıktı} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$

İkame, içindeki değerler Figure of merit DSBSC alıcı formülü.

$$ F = \ frac {\ left (SNR \ sağ) _ {O, DSBSC}} {\ left (SNR \ sağ) _ {C, DSBSC}} $$

$$ \ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ sağ) $$

$$ \ Rightarrow F = 1 $$

Bu nedenle, DSBSC alıcısının liyakat değeri 1'dir.

SSBSC Sisteminde SNR Hesaplamaları

Gürültüyü analiz etmek için SSBSC sisteminin aşağıdaki alıcı modelini düşünün.

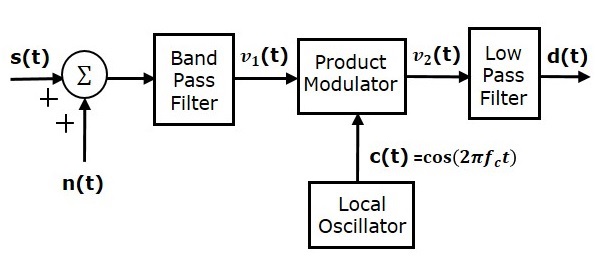
Daha düşük yan banda sahip olan SSBSC modülasyonlu dalganın

$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $$

SSBSC modülasyonlu dalganın ortalama gücü

$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$

Mesaj bant genişliğindeki ortalama gürültü gücü

$$ P_ {nc} = WN_0 $$

İkame, bu değerler channel SNR formül.

$$ \ left (SNR \ sağ) _ {C, SSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: SSBSC \: \: modüle edilmiş \: \: dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

Yukarıdaki şekilde gösterildiği gibi, bant geçiş gürültüsünün kanalda SSBSC ile modüle edilmiş dalga ile karıştırıldığını varsayın. Bu kombinasyon, ürün modülatörünün girdilerinden biri olarak uygulanır. Bu nedenle, bu ürün modülatörünün girişi

$$ v_1 \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$

$$ v_1 \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] + n_I \ sol (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) -n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) $$

Yerel osilatör $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $ taşıyıcı sinyalini üretir. Bu sinyal, ürün modülatörüne başka bir giriş olarak uygulanır. Bu nedenle, ürün modülatörü $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ 'ın çarpımı olan bir çıktı üretir.

$$ v_2 \ sol (t \ sağ) = v_1 \ sol (t \ sağ) c \ sol (t \ sağ) $$

Yukarıdaki denklemde $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini değiştirin.

$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $

$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ sağ) + $

$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $

$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ sağ) \ sağ \} + $

$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ sağ) - n_Q \ left (t \ sağ) \ frac {\ sin \ left (4 \ pi f_ct \ sağ)} {2} $

Yukarıdaki sinyal alçak geçiren filtreye giriş olarak uygulandığında, alçak geçiren filtre çıktısını şu şekilde alacağız:

$$ d \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ sağ) + \ frac {n_I \ left (t \ sağ)} {2} $$

Demodüle edilmiş sinyalin ortalama gücü

$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$

Çıkıştaki ortalama gürültü gücü

$$ P_ {no} = \ frac {WN_0} {4} $$

İkame, bu değerler output SNR formül

$$ \ left (SNR \ sağ) _ {O, SSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: çıktı} $$

$$ \ Rightarrow \ left (SNR \ sağ) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ sağ ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$

İkame, içindeki değerler Figure of merit SSBSC alıcı formülü

$$ F = \ frac {\ left (SNR \ sağ) _ {O, SSBSC}} {\ left (SNR \ sağ) _ {C, SSBSC}} $$

$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ sağ) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ sağ) $$

$$ F = 1 $$

Bu nedenle, SSBSC alıcısının liyakati değeri 1'dir.

Verici bölümünün sonunda bulunan anten, modüle edilmiş dalgayı iletir. Bu bölümde, AM ve FM vericileri hakkında tartışalım.

AM Verici

AM vericisi, ses sinyalini bir giriş olarak alır ve iletilecek bir çıkış olarak antene genlik modülasyonlu dalgayı gönderir. AM vericisinin blok şeması aşağıdaki şekilde gösterilmektedir.

AM vericinin çalışması aşağıdaki şekilde açıklanabilir.

• Mikrofonun çıkışından gelen ses sinyali, modüle edici sinyalin seviyesini artıran ön amplifikatöre gönderilir.

• RF osilatörü, taşıyıcı sinyali üretir.

• Hem modüle edici hem de taşıyıcı sinyal, AM modülatörüne gönderilir.

• Güç amplifikatörü, AM dalgasının güç seviyelerini artırmak için kullanılır. Bu dalga nihayet iletilmek üzere antene iletilir.

FM Verici

FM vericisi, ses sinyalini bir giriş olarak alan ve FM dalgasını iletilecek bir çıkış olarak antene ileten bütün birimdir. FM vericisinin blok şeması aşağıdaki şekilde gösterilmektedir.

FM vericinin çalışması şu şekilde açıklanabilir.

• Mikrofonun çıkışından gelen ses sinyali, modüle edici sinyalin seviyesini artıran ön amplifikatöre gönderilir.

• Bu sinyal daha sonra gürültüyü filtrelemek ve sinyal-gürültü oranını iyileştirmek için bir ön vurgu ağı görevi gören yüksek geçiş filtresine geçirilir.

• Bu sinyal ayrıca FM modülatör devresine aktarılır.

• Osilatör devresi, modüle edici sinyal ile birlikte modülatöre gönderilen yüksek frekanslı bir taşıyıcı üretir.

• Çalışma frekansını artırmak için birkaç frekans çarpanı aşaması kullanılır. O zaman bile, sinyalin gücü iletmek için yeterli değildir. Bu nedenle, modüle edilmiş sinyalin gücünü artırmak için sonunda bir RF güç amplifikatörü kullanılır. Bu FM modülasyonlu çıktı, en sonunda iletilmek üzere antene aktarılır.

Alıcı bölümünün başında bulunan anten, modüle edilmiş dalgayı alır. Önce bir alıcının gereksinimlerini tartışalım.

Alıcının Gereksinimleri

AM alıcısı, AM dalgasını alır ve zarf detektörünü kullanarak onu demodüle eder. Benzer şekilde, FM alıcısı da FM dalgasını alır ve Frekans Ayırım yöntemini kullanarak onu demodüle eder. Aşağıdakiler hem AM hem de FM alıcısının gereklilikleridir.

• Uygun maliyetli olmalı.

• Karşılık gelen modüle edilmiş dalgaları almalıdır.

• Alıcı, istenen istasyonu ayarlayabilmeli ve yükseltebilmelidir.

• İstenmeyen istasyonları reddetme yeteneğine sahip olmalıdır.

• Taşıyıcı sinyal frekansına bakılmaksızın tüm istasyon sinyallerine demodülasyon yapılmalıdır.

Bu gereksinimlerin karşılanması için, tuner devresi ve karıştırıcı devresi çok etkili olmalıdır. RF karıştırma prosedürü ilginç bir olgudur.

RF Karıştırma

RF karıştırma ünitesi bir Intermediate Frequency (IF), sinyali etkili bir şekilde işlemek için alınan herhangi bir sinyalin dönüştürüldüğü.

RF Mikser, alıcıda önemli bir aşamadır. Ortaya çıkan karışık çıktıyı üretmek için, bir sinyal seviyesinin diğer sinyalin seviyesini etkilediği yerde farklı frekanslarda iki sinyal alınır. Giriş sinyalleri ve elde edilen mikser çıkışı aşağıdaki şekillerde gösterilmektedir.

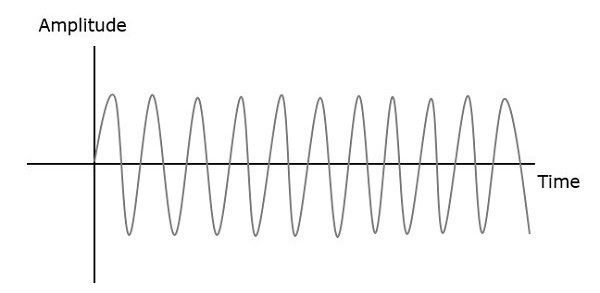
Birinci ve ikinci sinyal frekansları $ f_1 $ ve $ f_2 $ olsun. Bu iki sinyal RF mikserinin girişleri olarak uygulanırsa, o zaman frekansları $ f_1 + f_2 $ ve $ f_1-f_2 $ olan bir çıkış sinyali üretir.

Bu, frekans alanında gözlenirse, model aşağıdaki şekle benzer.

Bu durumda, $ f_1 $, $ f_2 $ 'dan büyüktür. Dolayısıyla, ortaya çıkan çıktının frekansları $ f_1 + f_2 $ ve $ f_1-f_2 $ olur. Benzer şekilde, $ f_2 $, $ f_1 $ 'dan büyükse, ortaya çıkan çıktı $ f_1 + f_2 $ ve $ f_1-f_2 $ frekanslarına sahip olacaktır.

AM Alıcı

AM süper heterodin alıcı, genlik modülasyonlu dalgayı bir giriş olarak alır ve bir çıkış olarak orijinal ses sinyalini üretir. Selectivity Diğerlerini reddederken belirli bir sinyali seçme yeteneğidir. Sensitivity en düşük güç seviyesindeyken RF sinyalini algılama ve demodüle etme kapasitesidir.

Radyo amatörleri ilk radyo alıcılarıdır. Ancak, zayıf duyarlılık ve seçicilik gibi dezavantajları vardır. Bu dezavantajların üstesinden gelmek için,super heterodynealıcı icat edildi. AM alıcısının blok şeması aşağıdaki şekilde gösterilmektedir.

RF Tuner Bölümü

Anten tarafından alınan genlik modülasyonlu dalga ilk önce tuner circuitbir transformatör aracılığıyla. Tuner devresi, aynı zamanda bir LC devresinden başka bir şey değildir.resonant veya tank circuit. AM alıcısının istediği frekansı seçer. Aynı zamanda yerel osilatör ve RF filtresini de ayarlar.

RF Mikser

Tuner çıkışından gelen sinyal alıcıya gönderilir. RF-IF converter, karıştırıcı görevi görür. Sabit bir frekans üreten yerel bir osilatöre sahiptir. Burada karıştırma işlemi, alınan sinyalin bir giriş ve yerel osilatör frekansının diğer giriş olmasıyla yapılır. Ortaya çıkan çıktı, karıştırıcı tarafından üretilen $ \ left [\ left (f_1 + f_2 \ right), \ left (f_1-f_2 \ right) \ right] $ iki frekansının bir karışımıdır ve bu,Intermediate Frequency (IF).

IF üretimi, herhangi bir taşıyıcı frekansa sahip herhangi bir istasyon sinyalinin demodülasyonuna yardımcı olur. Bu nedenle, tüm sinyaller yeterli seçicilik için sabit bir taşıyıcı frekansa çevrilir.

IF Filtresi

Ara frekans filtresi, istenen frekansı geçen bir bant geçiş filtresidir. İçinde bulunan diğer tüm istenmeyen frekans bileşenlerini ortadan kaldırır. Bu, yalnızca IF frekansına izin veren IF filtresinin avantajıdır.

AM Demodülatör

Alınan AM dalgası şimdi AM demodülatör kullanılarak demodüle edilir. Bu demodülatör, modülasyon sinyalini almak için zarf algılama sürecini kullanır.

Ses amplifikatörü

Bu, algılanan ses sinyalini yükseltmek için kullanılan güç amplifikatörü aşamasıdır. İşlenen sinyal, etkili olması için güçlendirilir. Bu sinyal, orijinal ses sinyalini almak için hoparlöre iletilir.

FM Alıcı

FM alıcısının blok şeması aşağıdaki şekilde gösterilmektedir.

FM alıcısının bu blok şeması, AM alıcısının blok şemasına benzer. İki bloklu Genlik sınırlayıcı ve Vurgu azaltma ağı, FM demodülatöründen önce ve sonra dahil edilmiştir. Kalan blokların çalışması, AM alıcısınınki ile aynıdır.

FM modülasyonunda FM dalgasının genliğinin sabit kaldığını biliyoruz. Ancak kanala FM dalgası ile bir miktar gürültü eklenirse, bundan dolayı FM dalgasının genliği değişebilir. Böylece, yardımıylaamplitude limiter Gürültü sinyalinin istenmeyen piklerini ortadan kaldırarak FM dalgasının genliğini sabit tutabiliriz.

FM vericide, FM modülatöründen önce mevcut olan ön vurgu ağını (Yüksek geçiş filtresi) gördük. Bu, yüksek frekanslı ses sinyalinin SNR'sini iyileştirmek için kullanılır. Ön vurgunun tersi süreç şu şekilde bilinir:de-emphasis. Bu nedenle, bu FM alıcısında, vurguyu azaltma ağı (Düşük geçiş filtresi) FM demodülatöründen sonra dahil edilir. Bu sinyal, güç seviyesini artırmak için ses yükselticisine iletilir. Son olarak, hoparlörden orijinal ses sinyalini alıyoruz.

Şimdiye kadar sürekli dalga modülasyonu hakkında tartıştık. Bir sonraki bölümde darbe modülasyonu hakkında tartışacağız. Bu darbe modülasyon teknikleri, ayrık sinyallerle ilgilenir. Öyleyse, şimdi sürekli bir zaman sinyalini ayrık olana nasıl dönüştürebileceğimizi görelim.

Sürekli zaman sinyallerini eşdeğer ayrık zaman sinyallerine dönüştürme işlemi şu şekilde adlandırılabilir: Sampling. Örnekleme sürecinde belirli bir anlık veri sürekli olarak örneklenir.

Aşağıdaki şekil sürekli zaman sinyalini göstermektedir x(t) ve karşılık gelen örneklenmiş sinyal x_s(t). Ne zamanx(t) periyodik bir dürtü katarı ile çarpılır, örneklenmiş sinyal x_s(t) elde edildi.

Bir sampling signal birim genliğe sahip, eşit zaman aralıklarında örneklenen, $ T_s $ olarak adlandırılan periyodik bir darbe dizisidir. sampling time. Bu veriler, $ T_s $ anında iletilir ve kalan zamanda taşıyıcı sinyal iletilir.

Örnekleme oranı

Sinyalleri ayırmak için numuneler arasındaki boşluk sabitlenmelidir. Bu boşluk, örnekleme dönemi $ T_s $ olarak adlandırılabilir. Örnekleme döneminin karşılıklı olarak bilinirsampling frequency veya sampling rate $f_s$.

Matematiksel olarak şöyle yazabiliriz

$$ f_s = \ frac {1} {T_s} $$

Nerede,

$ f_s $, örnekleme sıklığı veya örnekleme oranıdır

$ T_s $ örnekleme dönemidir

Örnekleme Teoremi

Örnekleme hızı, mesaj sinyalindeki verilerin kaybolmaması veya üst üste binmesi gerekecek şekilde olmalıdır. sampling theorem “bir sinyalin, verilen sinyalin maksimum frekansının iki katından büyük veya iki katına eşit olan $ f_s $ oranında örneklenmesi durumunda tam olarak yeniden üretilebileceğini belirtir. W. "

Matematiksel olarak şöyle yazabiliriz

$$ f_s \ geq 2W $$

Nerede,

• $ f_s $ örnekleme oranıdır

• $ W $, verilen sinyalin en yüksek frekansıdır

Örnekleme hızı, verilen sinyal W'nin maksimum frekansının iki katına eşitse, o zaman Nyquist rate.

Örnekleme teoremi olarak da adlandırılır Nyquist theorem, bantlı işlevler sınıfı için bant genişliği açısından yeterli örnekleme oranı teorisini sunar.

Sürekli zaman sinyali için x(t)frekans alanında bantla sınırlı olan aşağıdaki şekilde gösterildiği gibi temsil edilmektedir.

Sinyal Nyquist oranının üzerinde örneklenirse, orijinal sinyal geri kazanılabilir. Aşağıdaki şekil, şundan daha yüksek bir hızda örneklendiğinde bir sinyali açıklar.2w frekans alanında.

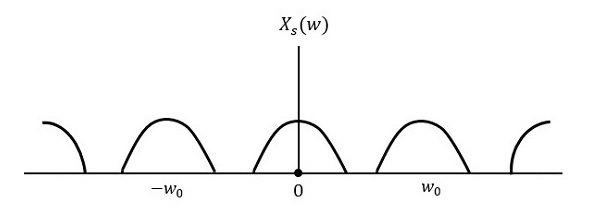
Aynı sinyal şu ​​değerden daha düşük bir hızda örneklenirse 2w, sonra örneklenen sinyal aşağıdaki şekle benzeyecektir.

Yukarıdaki modelden, bilginin üst üste binmesi olduğunu gözlemleyebiliriz, bu da karıştırmaya ve bilgi kaybına yol açar. Bu istenmeyen üst üste binme fenomenineAliasing.

Takma ad, "örneklenmiş versiyonunun spektrumundaki düşük frekanslı bir bileşenin kimliğini alan, bir sinyalin spektrumundaki yüksek frekanslı bir bileşen olgusu" olarak adlandırılabilir.

Bu nedenle, sinyalin örnekleme hızı Nyquist oranı olarak seçilmiştir. Örnekleme hızı, verilen sinyalin en yüksek frekansının iki katına eşitseW, sonra örneklenen sinyal aşağıdaki şekle benzeyecektir.

Bu durumda sinyal herhangi bir kayıp olmadan kurtarılabilir. Dolayısıyla, bu iyi bir örnekleme oranıdır.

Sürekli dalga modülasyonundan sonra, sonraki bölüm Darbe modülasyonudur. Bu bölümde, aşağıdaki analog darbe modülasyon tekniklerini tartışalım.

• Darbe Genlik Modülasyonu
• Darbe Genişliği Modülasyonu
• Darbe Konum Modülasyonu

Darbe Genlik Modülasyonu

İçinde Pulse Amplitude Modulation (PAM) teknikte, sinyal taşıyıcısının genliği, mesaj sinyalinin anlık genliği ile orantılı olarak değişir.

Darbe genliği modüle edilmiş sinyal, sinyal tüm dalganın yolunu izlerken orijinal sinyalin genliğini takip edecektir. Doğal PAM'de, Nyquist hızında örneklenen bir sinyal, verimli bir sistemden geçirilerek yeniden yapılandırılabilir.Low Pass Filter (LPF) kesin kesim frekansı ile.

Aşağıdaki şekiller Darbe Genlik Modülasyonunu açıklamaktadır.

PAM sinyali bir LPF'den geçmesine rağmen, distorsiyon olmadan sinyali kurtaramaz. Bu nedenle, bu gürültüyü önlemek için düz tepeli örnekleme kullanın. Düz tepeli PAM sinyali aşağıdaki şekilde gösterilmektedir.

Flat-top samplingörneklenen sinyalin, örneklenecek olan analog sinyale göre sinyal genliğinin değiştirilemediği darbelerde temsil edilebildiği süreçtir. Genliğin tepeleri düz kalır. Bu süreç devre tasarımını basitleştirir.

Darbe Genişliği Modülasyonu

İçinde Pulse Width Modulation (PWM) veya Darbe Süresi Modülasyonu (PDM) veya Darbe Süresi Modülasyonu (PTM) tekniğinde, sinyal taşıyıcısının genişliği veya süresi veya süresi, mesaj sinyalinin anlık genliği ile orantılı olarak değişir.

Darbenin genişliği bu yöntemde değişir, ancak sinyalin genliği sabit kalır. Genlik sınırlayıcılar, sinyalin genliğini sabit yapmak için kullanılır. Bu devreler, genliği istenen bir seviyeye düşürür ve dolayısıyla gürültü sınırlıdır.

Aşağıdaki şekil Darbe Genişliği Modülasyonlarının türlerini açıklamaktadır.

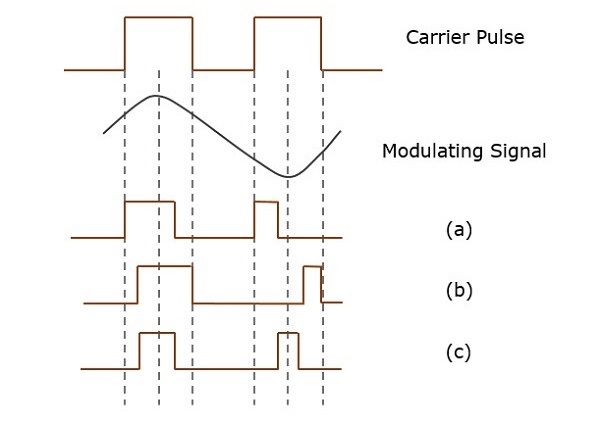
Üç tür PWM vardır.

• Darbenin ön kenarı sabittir, arka kenar mesaj sinyaline göre değişir. Bu tip PWM için dalga formu, yukarıdaki şekilde (a) olarak belirtilmiştir.

• Darbenin arka kenarı sabittir, ön kenar mesaj sinyaline göre değişir. Bu tip PWM için dalga formu, yukarıdaki şekilde (b) olarak belirtilmiştir.

• Darbenin merkezi sabittir, ön kenar ve arka kenar mesaj sinyaline göre değişir. Bu tip PWM için dalga formu, yukarıdaki şekilde gösterilen (c) olarak belirtilir.

Darbe Konum Modülasyonu

Pulse Position Modulation (PPM) darbelerin genliğinin ve genişliğinin sabit tutulduğu, bir referans darbesinin konumuna göre her darbenin konumunun mesaj sinyalinin anlık örneklenen değerine göre değiştiği bir analog modülasyon şemasıdır.

Verici ve alıcıyı senkronize tutmak için vericinin eşzamanlı darbeler göndermesi (veya basitçe eşzamanlı darbeler) gerekir. Bu eşzamanlı darbeler, darbelerin konumunun korunmasına yardımcı olur. Aşağıdaki şekiller Darbe Konum Modülasyonunu açıklamaktadır.

Darbe pozisyon modülasyonu, darbe genişliği modülasyonlu sinyale göre yapılır. Darbe genişliği modülasyonlu sinyalin her bir arka kenarı, PPM sinyalindeki darbeler için başlangıç ​​noktası olur. Bu nedenle, bu darbelerin konumu, PWM darbelerinin genişliği ile orantılıdır.

Avantaj

Genlik ve genişlik sabit olduğundan, kullanılan güç de sabittir.

Dezavantaj

Verici ve alıcı arasındaki senkronizasyon bir zorunluluktur.

PAM, PWM ve PPM arasında karşılaştırma

Aşağıdaki tablo, üç modülasyon tekniği arasındaki karşılaştırmayı göstermektedir.

PAM	PWM	PPM
Genlik çeşitlidir	Genişlik değişkendir	Pozisyon çeşitlidir
Bant genişliği darbenin genişliğine bağlıdır	Bant genişliği nabzın yükselme süresine bağlıdır	Bant genişliği nabzın yükselme süresine bağlıdır
Anlık verici gücü, darbelerin genliğine göre değişir	Anlık verici gücü, darbelerin genliği ve genişliğine göre değişir	Anlık verici gücü darbelerin genişliği ile sabit kalır
Sistem karmaşıklığı yüksek	Sistem karmaşıklığı düşük	Sistem karmaşıklığı düşük
Gürültü paraziti yüksek	Gürültü paraziti düşük	Gürültü paraziti düşük
Genlik modülasyonuna benzer	Frekans modülasyonuna benzer	Faz modülasyonuna benzer

Transducerenerjiyi bir formdan diğerine dönüştüren bir cihazdır. Bu bölümde, iletişim sistemlerinde kullanılan dönüştürücüleri tartışalım.

Neden Dönüştürücülere İhtiyacımız Var?

Gerçek dünyada, yakındaki herhangi iki kişi arasındaki iletişim ses dalgalarının yardımıyla gerçekleşir. Ancak kişiler uzakta ise, fiziksel formundaki ses dalgalarını kullanarak bilgiyi kayıpsız iletmek zordur.

Bu zorluğun üstesinden gelmek için verici bölümündeki modülatörleri, alıcı bölümündeki demodülatörleri kullanabiliriz. Bu modülatörler ve demodülatörler elektrik sinyalleri ile çalışır. Bu nedenle, ses dalgalarını elektrik sinyallerine veya tersine çevirmesi gereken bir cihaza ihtiyacımız var. Bu cihaz dönüştürücü olarak biliniyor.

Aşağıda, bir dönüştürücünün basit bir blok diyagramı verilmiştir.

Bu dönüştürücünün tek bir girişi ve tek bir çıkışı vardır. Girişte bulunan enerjiyi başka bir enerjiye sahip eşdeğer çıkışına dönüştürür. Temel olarak, bir dönüştürücü, elektriksel olmayan enerji biçimini elektriksel biçime dönüştürür veya bunun tersi de geçerlidir.

Dönüştürücü Türleri

Dönüştürücüleri aşağıdaki şekilde sınıflandırabiliriz two types dönüştürücünün iletişim sistemlerine yerleştirilmesine (konumuna) bağlıdır.

• Giriş Dönüştürücü
• Çıkış Dönüştürücü

Giriş Dönüştürücüleri

İletişim sisteminin girişinde bulunan dönüştürücü, bir input transducer. Aşağıda bir giriş dönüştürücünün blok şeması verilmiştir.

Bu giriş dönüştürücü, elektriksel olmayan fiziksel miktarı bir elektrik sinyaline dönüştürür. Ses veya ışık gibi fiziksel büyüklükler, bu dönüştürücü kullanılarak voltaj veya akım gibi elektriksel niceliklere dönüştürülebilir.Example: Mikrofon.

Mikrofon, bilgi kaynağı ile verici bölümü arasına yerleştirilen giriş dönüştürücü olarak kullanılır. Bilgi kaynağı, bilgiyi ses dalgaları şeklinde üretir. microphonebu ses dalgalarını bir diyafram yardımıyla elektrik sinyallerine dönüştürür. Bu elektrik sinyalleri daha fazla işlem için kullanılabilir.

Çıkış Dönüştürücüleri

İletişim sisteminin çıkışında bulunan dönüştürücü, çıkış dönüştürücü olarak bilinir. Aşağıda bir blok diyagramı verilmiştir.output transducer.

Bu çıkış dönüştürücü, elektrik sinyalini elektriksel olmayan fiziksel miktara dönüştürür. Gerilim veya akım gibi elektriksel büyüklükler, bu dönüştürücü kullanılarak ses veya ışık gibi fiziksel niceliklere dönüştürülebilir.Example: Hoparlör.

Hoparlör, alıcı bölümü ile hedef arasına yerleştirilen çıkış dönüştürücü olarak kullanılır. Alıcı bölümünde bulunan demodülatör, demodüle edilmiş çıkışı üretir. Böyleceloud speakerelektrik sinyallerini (demodüle edilmiş çıkış) ses dalgalarına dönüştürür. Bu nedenle, hoparlörün işlevselliği, mikrofonun işlevselliğinin tam tersidir.

Yukarıdaki dönüştürücülere ek olarak, iletişim sistemlerinde kullanılan bir dönüştürücü daha vardır. Bu dönüştürücü, verici bölümünün sonuna veya alıcı bölümünün başlangıcına yerleştirilebilir.Example: Anten.

Anten, elektrik sinyallerini elektromanyetik dalgalara ve tersi yönde dönüştüren bir dönüştürücüdür. Anten, birtransmitting antenna veya olarak receiving antenna.

Bir verici anten, elektrik sinyallerini elektromanyetik dalgalara dönüştürür ve yayar. Bir alıcı anten, alınan ışından gelen elektromanyetik dalgaları elektrik sinyallerine dönüştürür.

Bu iki yönlü iletişimde, aynı anten hem iletim hem de alım için kullanılabilir.