Analog Haberleşme - SNR Hesaplamaları
Bu bölümde, alıcıda demodüle edilen çeşitli modüle edilmiş dalgaların Sinyal-Gürültü Oranlarını ve Değer Şekillerini hesaplayalım.
Sinyal gürültü oranı
Signal-to-Noise Ratio (SNR)sinyal gücünün gürültü gücüne oranıdır. SNR değeri ne kadar yüksekse, alınan çıktının kalitesi de o kadar büyük olacaktır.
Farklı noktalardaki Sinyal-Gürültü Oranı aşağıdaki formüller kullanılarak hesaplanabilir.
Input SNR = $ \ left (SNR \ sağ) _I = \ frac {Ortalama \: \: güç \: \: / \: \: modülasyon \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: input} $
Output SNR = $ \ left (SNR \ sağ) _O = \ frac {Ortalama \: \: güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: çıktı} $
Channel SNR = $ \ left (SNR \ sağ) _C = \ frac {Ortalama \: \: güç \: \: / \: \: modüle edilmiş \: \: sinyal} {Ortalama \: \: güç \: \: / \: \: gürültü \: \: \: \: mesaj \: \: bant genişliği} $
Liyakat Figürü
Çıkış SNR ve giriş SNR oranı şu şekilde adlandırılabilir: Figure of Merit. İle gösterilirF. Bir cihazın performansını açıklar.
$$ F = \ frac {\ sol (SNR \ sağ) _O} {\ sol (SNR \ sağ) _I} $$
Bir alıcının liyakat değeri
$$ F = \ frac {\ sol (SNR \ sağ) _O} {\ sol (SNR \ sağ) _C} $$
Bu böyledir çünkü bir alıcı için kanal giriştir.
AM Sisteminde SNR Hesaplamaları
Gürültüyü analiz etmek için aşağıdaki AM sisteminin alıcı modelini düşünün.

Genlik Modülasyonlu (AM) dalgasının
$$ s \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) $$
$$ \ Rightarrow s \ left (t \ sağ) = A_c \ cos \ left (2 \ pi f_ct \ sağ) + A_ck_am \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$
AM dalgasının ortalama gücü
$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$
Mesaj bant genişliğindeki ortalama gürültü gücü
$$ P_ {nc} = WN_0 $$
İkame, bu değerler channel SNR formül
$$ \ left (SNR \ sağ) _ {C, AM} = \ frac {Ortalama \: \: Güç \: \: / \: \: AM \: \: Dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ sağ) P } {2WN_0} $$
Nerede,
P mesaj sinyalinin gücü = $ \ frac {{A_ {m}} ^ {2}} {2} $
W mesaj bant genişliği
Yukarıdaki şekilde gösterildiği gibi bant geçiş gürültüsünün kanaldaki AM dalgasıyla karıştırıldığını varsayın. Bu kombinasyon, AM demodülatörünün girişine uygulanır. Bu nedenle, AM demodülatörünün girişi.
$$ v \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$
$ \ Rightarrow v \ left (t \ sağ) = A_c \ left [1 + k_am \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ right) + $
$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ sağ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ] $
$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ sağ) + n_1 \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) $
$ N_I \ left (t \ right) $ ve $ n_Q \ left (t \ right) $, gürültünün faz ve kuadratür faz bileşenlerindeyken.
AM demodülatörünün çıkışı, yukarıdaki sinyalin zarfından başka bir şey değildir.
$$ d \ left (t \ sağ) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ sağ) \ sağ] ^ 2 + \ left (n_Q \ left (t \ sağ) \ sağ) ^ 2} $$
$$ \ Rightarrow d \ sol (t \ sağ) \ yaklaşık A_c + A_ck_am \ sol (t \ sağ) + n_1 \ sol (t \ sağ) $$
Demodüle edilmiş sinyalin ortalama gücü
$$ P_m = \ left (\ frac {A_ck_am \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
Çıkıştaki ortalama gürültü gücü
$$ P_no = WN_0 $$
İkame, bu değerler output SNR formül.
$$ \ left (SNR \ sağ) _ {O, AM} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: Çıktı} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
İkame, içindeki değerler Figure of merit AM alıcı formülü.
$$ F = \ frac {\ left (SNR \ sağ) _ {O, AM}} {\ left (SNR \ sağ) _ {C, AM}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ sağ) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
Bu nedenle, AM alıcısının liyakat figürü birden azdır.
DSBSC Sisteminde SNR Hesaplamaları
Gürültüyü analiz etmek için DSBSC sisteminin aşağıdaki alıcı modelini düşünün.

DSBSC modülasyonlu dalganın
$$ s \ left (t \ sağ) = A_cm \ left (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$
DSBSC modülasyonlu dalganın ortalama gücü
$$ P_s = \ left (\ frac {A_cm \ left (t \ sağ)} {\ sqrt {2}} \ sağ) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
Mesaj bant genişliğindeki ortalama gürültü gücü
$$ P_ {nc} = WN_0 $$
İkame, bu değerler channel SNR formül.
$$ \ left (SNR \ sağ) _ {C, DSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: DSBSC \: \: modüle edilmiş \: \: dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
Yukarıdaki şekilde gösterildiği gibi, bant geçiş gürültüsünün kanalda DSBSC ile modüle edilmiş dalga ile karıştırıldığını varsayın. Bu kombinasyon, ürün modülatörünün girdilerinden biri olarak uygulanır. Bu nedenle, bu ürün modülatörünün girişi
$$ v_1 \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$
$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ sağ) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ sağ) - n_Q \ sol (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ] $$
$$ \ Rightarrow v_1 \ left (t \ sağ) = \ sol [A_cm \ sol (t \ sağ) + n_I \ sol (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ sağ) $$
Yerel osilatör $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $ taşıyıcı sinyalini üretir. Bu sinyal, ürün modülatörüne başka bir giriş olarak uygulanır. Bu nedenle, ürün modülatörü $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ 'ın çarpımı olan bir çıktı üretir.
$$ v_2 \ sol (t \ sağ) = v_1 \ sol (t \ sağ) c \ sol (t \ sağ) $$
Yukarıdaki denklemde $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini değiştirin.
$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ] \ cos \ left (2 \ pi f_ct \ sağ ) - n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ] \ cos ^ 2 \ left (2 \ pi f_ct \ sağ ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ sağ) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ sağ)} {2} \ sağ) -n_Q \ sol (t \ sağ) \ frac {\ sin \ left (4 \ pi f_ct \ sağ)} {2} $$
Yukarıdaki sinyal alçak geçiren filtreye giriş olarak uygulandığında, alçak geçiren filtre çıktısını şu şekilde alacağız:
$$ d \ left (t \ sağ) = \ frac {\ left [A_c m \ left (t \ sağ) + n_I \ left (t \ sağ) \ sağ]} {2} $$
Demodüle edilmiş sinyalin ortalama gücü
$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
Çıkıştaki ortalama gürültü gücü
$$ P_ {no} = \ frac {WN_0} {4} $$
İkame, bu değerler output SNR formül.
$$ \ left (SNR \ sağ) _ {O, DSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: Çıktı} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
İkame, içindeki değerler Figure of merit DSBSC alıcı formülü.
$$ F = \ frac {\ left (SNR \ sağ) _ {O, DSBSC}} {\ left (SNR \ sağ) _ {C, DSBSC}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ sağ) $$
$$ \ Rightarrow F = 1 $$
Bu nedenle, DSBSC alıcısının liyakat değeri 1'dir.
SSBSC Sisteminde SNR Hesaplamaları
Gürültüyü analiz etmek için SSBSC sisteminin aşağıdaki alıcı modelini düşünün.
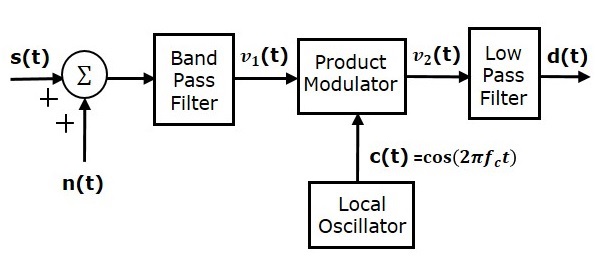
Daha düşük yan banda sahip olan SSBSC modülasyonlu dalganın
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] $$
SSBSC modülasyonlu dalganın ortalama gücü
$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
Mesaj bant genişliğindeki ortalama gürültü gücü
$$ P_ {nc} = WN_0 $$
İkame, bu değerler channel SNR formül.
$$ \ left (SNR \ sağ) _ {C, SSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: SSBSC \: \: modüle edilmiş \: \: dalga} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: içinde \: \: mesaj \: \: bant genişliği} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
Yukarıdaki şekilde gösterildiği gibi, bant geçiş gürültüsünün kanalda SSBSC ile modüle edilmiş dalga ile karıştırıldığını varsayın. Bu kombinasyon, ürün modülatörünün girdilerinden biri olarak uygulanır. Bu nedenle, bu ürün modülatörünün girişi
$$ v_1 \ left (t \ sağ) = s \ sol (t \ sağ) + n \ sol (t \ sağ) $$
$$ v_1 \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ sağ) t \ sağ] + n_I \ sol (t \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) -n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) $$
Yerel osilatör $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $ taşıyıcı sinyalini üretir. Bu sinyal, ürün modülatörüne başka bir giriş olarak uygulanır. Bu nedenle, ürün modülatörü $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ 'ın çarpımı olan bir çıktı üretir.
$$ v_2 \ sol (t \ sağ) = v_1 \ sol (t \ sağ) c \ sol (t \ sağ) $$
Yukarıdaki denklemde $ v_1 \ left (t \ right) $ ve $ c \ left (t \ right) $ değerlerini değiştirin.
$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $
$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ sağ) + $
$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ sağ) \ sin \ left (2 \ pi f_ct \ sağ) \ cos \ left (2 \ pi f_ct \ sağ) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ sağ) \ sağ \} + $
$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ sağ) - n_Q \ left (t \ sağ) \ frac {\ sin \ left (4 \ pi f_ct \ sağ)} {2} $
Yukarıdaki sinyal alçak geçiren filtreye giriş olarak uygulandığında, alçak geçiren filtre çıktısını şu şekilde alacağız:
$$ d \ left (t \ sağ) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ sağ) + \ frac {n_I \ left (t \ sağ)} {2} $$
Demodüle edilmiş sinyalin ortalama gücü
$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
Çıkıştaki ortalama gürültü gücü
$$ P_ {no} = \ frac {WN_0} {4} $$
İkame, bu değerler output SNR formül
$$ \ left (SNR \ sağ) _ {O, SSBSC} = \ frac {Ortalama \: \: Güç \: \: / \: \: demodüle edilmiş \: \: sinyal} {Ortalama \: \: Güç \: \: / \: \: gürültü \: \: \: \: çıktı} $$
$$ \ Rightarrow \ left (SNR \ sağ) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ sağ ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
İkame, içindeki değerler Figure of merit SSBSC alıcı formülü
$$ F = \ frac {\ left (SNR \ sağ) _ {O, SSBSC}} {\ left (SNR \ sağ) _ {C, SSBSC}} $$
$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ sağ) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ sağ) $$
$$ F = 1 $$
Bu nedenle, SSBSC alıcısının liyakati değeri 1'dir.