Analisis Keuangan Data Excel

Anda dapat melakukan analisis keuangan dengan Excel dengan cara yang mudah. Excel memberi Anda beberapa fungsi keuangan seperti PMT, PV, NPV, XNPV, IRR, MIRR, XIRR, dan sebagainya yang memungkinkan Anda untuk dengan cepat sampai pada hasil analisis keuangan.

Dalam bab ini, Anda akan mempelajari di mana dan bagaimana Anda dapat menggunakan fungsi-fungsi ini untuk analisis Anda.

Apa itu Anuitas?

Anuitas adalah rangkaian pembayaran tunai konstan yang dilakukan selama periode berkelanjutan. Misalnya, tabungan untuk pensiun, pembayaran asuransi, pinjaman rumah, hipotek, dll. Dalam fungsi anuitas -

Angka positif mewakili uang tunai yang diterima.
Angka negatif menunjukkan pembayaran tunai.

Nilai Sekarang dari serangkaian Pembayaran Masa Depan

Nilai saat ini adalah jumlah total nilai dari serangkaian pembayaran di masa mendatang sekarang. Anda dapat menghitung nilai sekarang menggunakan fungsi Excel -

PV- Menghitung nilai sekarang dari investasi dengan menggunakan suku bunga dan serangkaian pembayaran masa depan (nilai negatif) dan pendapatan (nilai positif). Setidaknya satu dari arus kas harus positif dan setidaknya satu harus negatif.
NPV - Menghitung nilai bersih sekarang dari investasi dengan menggunakan tingkat diskonto dan serangkaian pembayaran periodik masa depan (nilai negatif) dan pendapatan (nilai positif).
XNPV - Menghitung nilai bersih sekarang untuk jadwal arus kas yang tidak selalu berkala.

Note that -

Arus kas PV harus konstan sedangkan arus kas NPV dapat bervariasi.
Arus kas PV dapat berupa di awal atau di akhir periode sedangkan arus kas NPV harus di akhir periode.
Arus kas NPV harus periodik sedangkan arus kas XNPV tidak perlu periodik.

Di bagian ini, Anda akan memahami cara bekerja dengan PV. Anda akan mempelajari tentang NPV di bagian selanjutnya.

Contoh

Misalkan Anda membeli lemari es. Penjual memberi tahu Anda bahwa harga lemari es adalah 32000, tetapi Anda memiliki opsi untuk membayar jumlah tersebut dalam 8 tahun dengan tingkat bunga 13% per tahun dan pembayaran tahunan 6000. Anda juga memiliki opsi untuk melakukan pembayaran baik di awal atau akhir setiap tahun.

Anda ingin tahu opsi mana yang bermanfaat bagi Anda.

Anda dapat menggunakan fungsi Excel PV -

PV (rate, nper, pmt, [fv ], [type])

Untuk menghitung nilai sekarang dengan pembayaran pada akhir setiap tahun, hilangkan tipe atau tentukan 0 untuk tipe.

Untuk menghitung nilai sekarang dengan pembayaran setiap akhir tahun, tentukan 1 untuk jenisnya.

Anda akan mendapatkan hasil sebagai berikut -

Karena itu,

Jika Anda melakukan pembayaran sekarang, Anda harus membayar 32.000 dari nilai sekarang.
Jika Anda memilih pembayaran tahunan dengan pembayaran di akhir tahun, Anda perlu membayar 28.793 dari nilai sekarang.
Jika Anda memilih pembayaran tahunan dengan pembayaran di akhir tahun, Anda harus membayar 32.536 dari nilai sekarang.

Anda dapat dengan jelas melihat bahwa opsi 2 bermanfaat bagi Anda.

Apakah EMI itu?

Angsuran Bulanan yang Bersamaan (EMI) didefinisikan oleh Investopedia sebagai "Jumlah pembayaran tetap yang dilakukan oleh peminjam kepada pemberi pinjaman pada tanggal tertentu setiap bulan kalender. Angsuran bulanan yang disamakan digunakan untuk melunasi bunga dan pokok setiap bulan, sehingga melebihi dalam beberapa tahun tertentu, pinjaman itu lunas. "

EMI dengan Pinjaman

Di Excel, Anda dapat menghitung EMI pinjaman dengan fungsi PMT.

Misalkan, Anda ingin mengambil pinjaman rumah 5000000 dengan tingkat bunga tahunan 11,5% dan jangka waktu pinjaman selama 25 tahun. Anda dapat menemukan EMI Anda sebagai berikut -

Hitung suku bunga per bulan (Suku Bunga per Tahun / 12)
Hitung jumlah pembayaran bulanan (Jumlah tahun * 12)
Gunakan fungsi PMT untuk menghitung EMI

Saat Anda mengamati,

Present Value (PV) adalah jumlah pinjaman.
Nilai Masa Depan (FV) adalah 0 karena pada akhir jangka waktu jumlah pinjaman harus 0.
Ketik adalah 1 karena EMI dibayarkan di awal setiap bulan.

Anda akan mendapatkan hasil sebagai berikut -

Pembayaran Bulanan Pokok dan Bunga Pinjaman

EMI mencakup pembayaran bunga dan sebagian pokok. Seiring bertambahnya waktu, kedua komponen EMI ini akan bervariasi, mengurangi keseimbangan.

Mendapatkan

Bagian bunga dari pembayaran bulanan Anda, Anda dapat menggunakan fungsi Excel IPMT.
Pembayaran pokok pembayaran bulanan Anda, Anda dapat menggunakan fungsi Excel PPMT.

Misalnya, jika Anda telah mengambil pinjaman 1.000.000 untuk jangka waktu 8 bulan dengan tingkat bunga 16% per tahun. Anda bisa mendapatkan nilai untuk EMI, jumlah bunga yang menurun, pembayaran jumlah pokok yang meningkat dan saldo pinjaman yang berkurang selama 8 bulan. Setelah 8 bulan, saldo pinjaman menjadi 0.

Ikuti prosedur yang diberikan di bawah ini.

Step 1 - Hitung EMI sebagai berikut.

Ini menghasilkan EMI sebesar Rs. 13261.59.

Step 2 - Selanjutnya hitung bunga dan pokok EMI selama 8 bulan seperti gambar di bawah ini.

Anda akan mendapatkan hasil sebagai berikut.

Bunga dan Pokok dibayarkan antara dua Periode

Anda dapat menghitung bunga dan pokok yang dibayarkan antara dua periode, inklusif.

Menghitung bunga kumulatif yang dibayar antara 2 ^nd dan 3 ^rd bulan menggunakan fungsi CUMIPMT.
Memverifikasi hasil menjumlahkan nilai bunga untuk 2 ^nd dan 3 ^rd bulan.
Hitunglah pokok kumulatif yang dibayar antara 2 ^nd dan 3 ^rd bulan menggunakan fungsi IPMT.
Memverifikasi hasil menjumlahkan nilai utama untuk 2 ^nd dan 3 ^rd bulan.

Anda akan mendapatkan hasil sebagai berikut.

Anda dapat melihat bahwa perhitungan Anda cocok dengan hasil verifikasi Anda.

Menghitung Suku Bunga

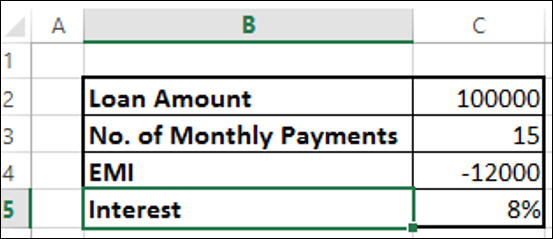
Misalkan Anda mengambil pinjaman 100.000 dan Anda ingin membayar kembali dalam 15 bulan dengan pembayaran bulanan maksimum 12.000. Anda mungkin ingin mengetahui tingkat bunga yang harus Anda bayar.

Temukan suku bunga dengan fungsi Excel RATE -

Anda akan mendapatkan hasil sebagai 8%.

Menghitung Jangka Waktu Pinjaman

Misalkan Anda mengambil pinjaman 100.000 dengan tingkat bunga 10%. Anda menginginkan pembayaran bulanan maksimum 15.000. Anda mungkin ingin tahu berapa lama waktu yang Anda butuhkan untuk melunasi pinjaman.

Temukan jumlah pembayaran dengan fungsi Excel NPER

Anda akan mendapatkan hasilnya sebagai 12 bulan.

Keputusan tentang Investasi

Ketika Anda ingin melakukan investasi, Anda membandingkan opsi-opsi yang berbeda dan memilih salah satu yang menghasilkan pengembalian yang lebih baik. Nilai bersih saat ini berguna untuk membandingkan arus kas selama periode waktu tertentu dan memutuskan mana yang lebih baik. Arus kas dapat terjadi pada interval reguler, berkala atau pada interval yang tidak teratur.

Pertama, kami mempertimbangkan kasus regular, periodical cash flows.

Nilai bersih sekarang dari urutan arus kas yang diterima pada titik waktu yang berbeda dalam n tahun dari sekarang (n dapat berupa pecahan) adalah 1/(1 + r)ⁿ, di mana r adalah tingkat bunga tahunan.

Pertimbangkan dua investasi berikut selama 3 tahun.

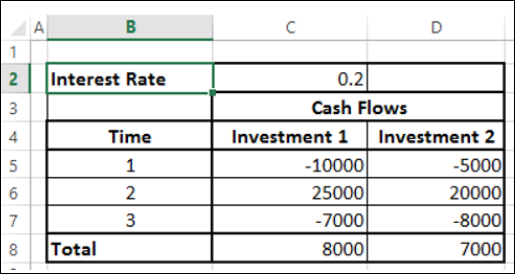
Pada nilai nominal, Investasi 1 terlihat lebih baik daripada Investasi 2. Namun, Anda dapat memutuskan investasi mana yang lebih baik hanya jika Anda mengetahui nilai sebenarnya dari investasi tersebut pada hari ini. Anda dapat menggunakan fungsi NPV untuk menghitung pengembalian.

Arus kas dapat terjadi

Setiap akhir tahun.
Di awal setiap tahun.
Di tengah setiap tahun.

Fungsi NPV mengasumsikan arus kas berada pada akhir tahun. Jika arus kas terjadi pada waktu yang berbeda maka Anda harus memperhitungkan faktor tersebut bersama dengan perhitungan dengan NPV.

Misalkan arus kas terjadi pada akhir tahun. Kemudian Anda dapat langsung menggunakan fungsi NPV.

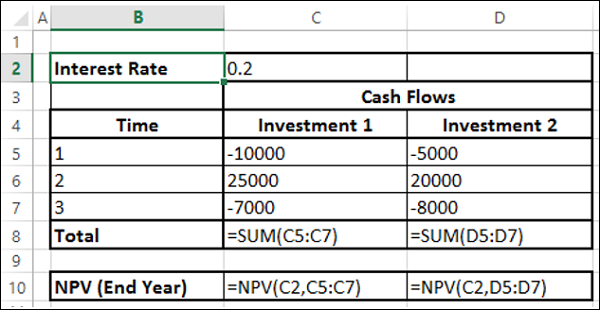
Anda akan mendapatkan hasil sebagai berikut -

Seperti yang Anda amati, NPV untuk Investasi 2 lebih tinggi daripada untuk Investasi 1. Oleh karena itu, Investasi 2 adalah pilihan yang lebih baik. Anda mendapatkan hasil ini karena arus kas keluar untuk Investasi 2 berada di periode selanjutnya dibandingkan dengan Investasi 1.

Arus Kas di Awal Tahun

Misalkan arus kas terjadi setiap awal tahun. Dalam kasus seperti itu, Anda tidak boleh memasukkan arus kas pertama dalam perhitungan NPV karena sudah mewakili nilai saat ini. Anda perlu menambahkan arus kas pertama ke NPV yang diperoleh dari sisa arus kas untuk mendapatkan nilai bersih sekarang.

Anda akan mendapatkan hasil sebagai berikut -

Arus Kas di Tengah Tahun

Misalkan arus kas terjadi setiap pertengahan tahun. Dalam kasus seperti itu, Anda perlu mengalikan NPV yang diperoleh dari arus kas dengan $ \ sqrt {1 + r} $ untuk mendapatkan nilai bersih sekarang.

Anda akan mendapatkan hasil sebagai berikut -

Arus Kas pada Interval Tidak Teratur

Jika Anda ingin menghitung nilai sekarang bersih dengan arus kas tidak teratur, yaitu arus kas yang terjadi pada waktu acak, perhitungannya agak rumit.

Namun, di Excel, Anda dapat dengan mudah melakukan penghitungan tersebut dengan fungsi XNPV.

Atur data Anda dengan tanggal dan arus kas.

Note- Tanggal pertama dalam data Anda harus paling awal dari semua tanggal. Tanggal lain dapat muncul dalam urutan apa pun.

Gunakan fungsi XNPV untuk menghitung nilai bersih sekarang.

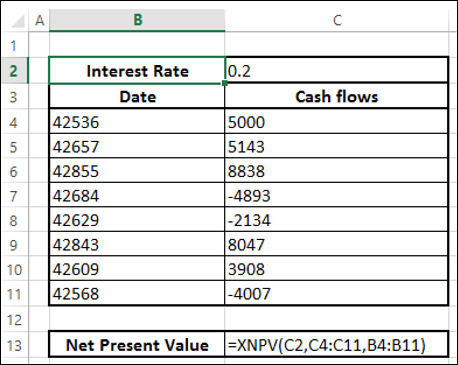
Anda akan mendapatkan hasil sebagai berikut -

Tanggal Misalkan hari ini adalah 15 ^th Maret 2015. Anda amati, semua tanggal arus kas yang dari tanggal kemudian. Jika Anda ingin mencari nilai bersih sekarang untuk hari ini, masukkan ke dalam data di bagian atas dan tentukan 0 untuk arus kas.

Anda akan mendapatkan hasil sebagai berikut -

Tingkat Pengembalian Internal (IRR)

Tingkat Pengembalian Internal (IRR) dari sebuah investasi adalah tingkat bunga di mana NPV adalah 0. Ini adalah nilai tingkat di mana nilai sekarang dari arus kas positif secara tepat mengkompensasi yang negatif. Ketika tingkat diskonto adalah IRR, investasi menjadi sangat acuh tak acuh, yaitu investor tidak mendapatkan atau kehilangan uang.

Pertimbangkan arus kas berikut, suku bunga yang berbeda dan nilai NPV yang sesuai.

Seperti yang bisa Anda amati antara nilai suku bunga 10% dan 11%, tanda NPV berubah. Jika Anda menyesuaikan tingkat suku bunga menjadi 10,53%, NPV hampir 0. Jadi, IRR adalah 10,53%.

Menentukan IRR Arus Kas untuk Proyek

Anda dapat menghitung IRR arus kas dengan fungsi Excel IRR.

IRR adalah 10,53% seperti yang Anda lihat di bagian sebelumnya.

Untuk arus kas tertentu, IRR dapat -

ada dan unik
ada dan banyak
tidak ada

IRR unik

Jika IRR ada dan unik, IRR dapat digunakan untuk memilih investasi terbaik di antara beberapa kemungkinan.

Jika arus kas pertama negatif, itu berarti investor memiliki uang dan ingin berinvestasi. Kemudian, semakin tinggi IRR semakin baik, karena ini mewakili tingkat bunga yang diterima investor.
Jika arus kas pertama positif, itu berarti investor membutuhkan uang dan sedang mencari pinjaman, semakin rendah IRR semakin baik karena mewakili tingkat bunga yang dibayarkan investor.

Untuk mengetahui apakah IRR unik atau tidak, ubah nilai tebakan dan hitung IRR. Jika IRR tetap konstan maka itu unik.

Seperti yang Anda amati, IRR memiliki nilai unik untuk nilai tebakan yang berbeda.

Beberapa IRR

Dalam kasus tertentu, Anda mungkin memiliki beberapa IRR. Pertimbangkan arus kas berikut. Hitung IRR dengan nilai tebakan berbeda.

Anda akan mendapatkan hasil sebagai berikut -

Anda dapat mengamati bahwa ada dua IRR - -9,59% dan 216,09%. Anda dapat memverifikasi kedua IRR yang menghitung NPV ini.

Untuk -9,59% dan 216,09%, NPV adalah 0.

Tidak ada IRR

Dalam kasus tertentu, Anda mungkin tidak memiliki IRR. Pertimbangkan arus kas berikut. Hitung IRR dengan nilai tebakan berbeda.

Anda akan mendapatkan hasil sebagai #NUM untuk semua nilai tebakan.

Hasil #NUM berarti tidak ada IRR untuk arus kas yang dipertimbangkan.

Pola Arus Kas dan IRR

Jika hanya ada satu tanda perubahan arus kas, seperti dari negatif ke positif atau positif ke negatif, maka IRR unik dijamin. Misalnya, dalam investasi modal, arus kas pertama akan negatif, sedangkan arus kas sisanya akan positif. Dalam kasus seperti itu, IRR unik ada.

Jika ada lebih dari satu tanda perubahan arus kas, IRR mungkin tidak ada. Bahkan jika itu ada, itu mungkin tidak unik.

Keputusan berdasarkan IRR

Banyak analis lebih suka menggunakan IRR dan ini adalah ukuran profitabilitas yang populer karena, sebagai persentase, mudah dipahami dan mudah dibandingkan dengan pengembalian yang diperlukan. Namun, ada masalah tertentu saat mengambil keputusan dengan IRR. Jika Anda memberi peringkat dengan IRR dan membuat keputusan berdasarkan peringkat ini, Anda mungkin berakhir dengan keputusan yang salah.

Anda telah melihat bahwa NPV akan memungkinkan Anda membuat keputusan finansial. Namun, IRR dan NPV tidak akan selalu menghasilkan keputusan yang sama jika proyek saling eksklusif.

Mutually exclusive projectsadalah proyek di mana pemilihan satu proyek menghalangi penerimaan proyek lainnya. Jika proyek yang dibandingkan bersifat eksklusif, konflik peringkat dapat muncul antara NPV dan IRR. Jika Anda harus memilih antara proyek A dan proyek B, NPV mungkin menyarankan penerimaan proyek A sedangkan IRR mungkin menyarankan proyek B.

Jenis konflik antara NPV dan IRR ini mungkin muncul karena salah satu alasan berikut -

Proyek memiliki ukuran yang sangat berbeda, atau
Waktu arus kas berbeda.

Proyek dengan perbedaan ukuran yang signifikan

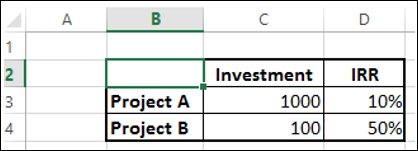
Jika Anda ingin membuat keputusan dengan IRR, proyek A menghasilkan pengembalian 100 dan Proyek B pengembalian 50. Oleh karena itu, investasi pada proyek A terlihat menguntungkan. Namun, ini adalah keputusan yang salah karena perbedaan skala proyek.

Pertimbangkan -

Anda memiliki 1000 untuk diinvestasikan.
Jika Anda menginvestasikan seluruh 1000 pada proyek A, Anda mendapatkan pengembalian 100.
Jika Anda berinvestasi 100 pada proyek B, Anda masih memiliki 900 di tangan Anda sehingga Anda dapat berinvestasi pada proyek lain, katakanlah proyek C. Misalkan Anda mendapatkan pengembalian 20% pada proyek C, maka total laba atas proyek B dan proyek C adalah 230, yang jauh di depan dalam profitabilitas.

Jadi, NPV adalah cara yang lebih baik untuk pengambilan keputusan dalam kasus seperti itu.

Proyek dengan pengaturan waktu arus kas yang berbeda

Sekali lagi, jika Anda mempertimbangkan IRR untuk memutuskan, proyek B akan menjadi pilihan. Namun, proyek A memiliki NPV yang lebih tinggi dan merupakan pilihan ideal.

IRR Arus Kas Tidak Beraturan (XIRR)

Arus kas Anda terkadang berjarak tidak teratur. Dalam kasus seperti itu, Anda tidak dapat menggunakan IRR karena IRR memerlukan interval waktu yang sama. Anda dapat menggunakan XIRR sebagai gantinya, yang memperhitungkan tanggal arus kas bersama dengan arus kas.

Tingkat Pengembalian Internal yang dihasilkan adalah 26,42%.

IRR yang dimodifikasi (MIRR)

Pertimbangkan kasus ketika tingkat keuangan Anda berbeda dari tingkat investasi ulang Anda. Jika Anda menghitung Tingkat Pengembalian Internal dengan IRR, ini mengasumsikan tingkat yang sama untuk keuangan dan investasi ulang. Selanjutnya, Anda mungkin juga mendapatkan banyak IRR.

Misalnya, perhatikan arus kas yang diberikan di bawah ini -

Seperti yang Anda amati, NPV adalah 0 lebih dari sekali, menghasilkan banyak IRR. Selanjutnya, tingkat investasi kembali tidak diperhitungkan. Dalam kasus seperti itu, Anda dapat menggunakan IRR yang dimodifikasi (MIRR).

Anda akan mendapatkan hasil 7% seperti yang ditunjukkan di bawah ini -

Note - Tidak seperti IRR, MIRR akan selalu unik.