Statistiche - Distribuzione chi quadrato

La distribuzione chi quadrato (chi quadrato o $ {X ^ 2} $ - distribuzione) con gradi di libertà, k è la distribuzione di una somma dei quadrati di k variabili casuali normali standard indipendenti. È una delle distribuzioni di probabilità più utilizzate in statistica. È un caso speciale della distribuzione gamma.

La distribuzione del chi quadrato è ampiamente utilizzata dagli statistici per calcolare quanto segue:

Stima dell'intervallo di confidenza per una deviazione standard della popolazione di una distribuzione normale utilizzando una deviazione standard del campione.
Verificare l'indipendenza di due criteri di classificazione di più variabili qualitative.
Per controllare le relazioni tra variabili categoriali.
Studiare la varianza campionaria dove la distribuzione sottostante è normale.
Per testare le deviazioni delle differenze tra le frequenze attese e osservate.
Per condurre un test del chi-quadrato (un test di bontà di adattamento).

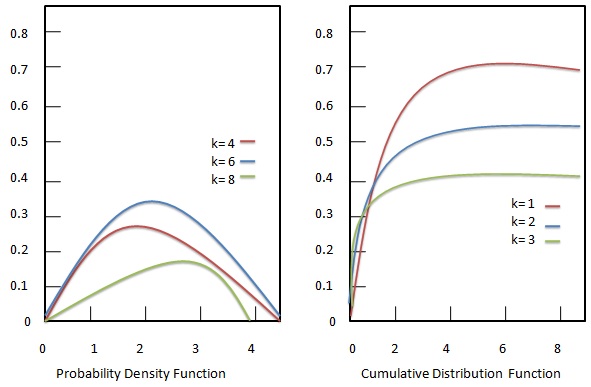
Densità di probabilità

La funzione di densità di probabilità della distribuzione Chi-quadrato è data come:

Formula

$ {f (x; k) =} $ $ \ begin {case} \ frac {x ^ {\ frac {k} {2} - 1} e ^ {- \ frac {x} {2}}} {2 ^ {\ frac {k} {2}} \ Gamma (\ frac {k} {2})}, & \ text {if $ x \ gt 0 $} \\ [7pt] 0, & \ text {if $ x \ le 0 $} \ end {cases} $

Dove -

$ {\ Gamma (\ frac {k} {2})} $ = Funzione gamma con valori in forma chiusa per il parametro intero k.
$ {x} $ = variabile casuale.
$ {k} $ = parametro intero.