Statistiche - Confronto di grafici
I gruppi di popolazione possono essere confrontati utilizzando grafici a scatola e baffi. La diffusione complessiva visibile e la differenza tra la mediana viene utilizzata per trarre la conclusione che tende ad essere una differenza tra due gruppi o meno.
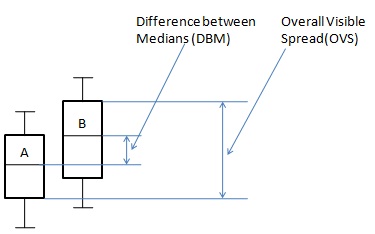
Caso 2: Formula
$ {P = \ frac {DBM} {OVS} \ times 100} $
Dove -
$ {P} $ = differenza percentuale
$ {DBM} $ = Differenza tra le medie.
$ {OVS} $ = Diffusione visibile complessiva.
Regole
Per una dimensione del campione di 30, se questa percentuale è maggiore del 33%, tende a esserci una differenza tra due gruppi.
Per una dimensione del campione di 100, se questa percentuale è maggiore del 20%, tende a esserci una differenza tra due gruppi.
Per una dimensione del campione di 1000, se questa percentuale è maggiore del 10%, tende ad esserci una differenza tra due gruppi.
Esempio
Dichiarazione problema:
Descrivi la differenza tra le seguenti serie di dati.
| Sr. No. | Nome | Imposta A | Imposta B |
|---|---|---|---|
| 1 | Max | 12 | 15 |
| 2 | UQ | 10 | 13 |
| 3 | Mediano | 7 | 10 |
| 4 | LQ | 6 | 9 |
| 5 | Min | 5 | 6 |
Soluzione:
Considera il seguente diagramma:
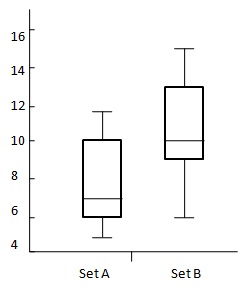
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10 -3 \\ [7pt] \ = 4} $
Applica la formula
$ {P = \ frac {DBM} {OVS} \ times 100 \\ [7pt] \ = \ frac {4} {7} \ times 100 \\ [7pt] \ = 57,14} $
Poiché la percentuale è superiore al 33%, esiste una differenza tra l'insieme A e l'insieme B. È probabile che l'insieme B sia maggiore dell'insieme A.