Statistiche - Distribuzione gamma
La distribuzione gamma rappresenta le distribuzioni di probabilità continue della famiglia a due parametri. Le distribuzioni gamma sono concepite con generalmente tre tipi di combinazioni di parametri.
Un parametro di forma $ k $ e un parametro di scala $ \ theta $.
Un parametro di forma $ \ alpha = k $ e un parametro di scala inverso $ \ beta = \ frac {1} {\ theta} $, chiamato parametro di velocità.
Un parametro di forma $ k $ e un parametro medio $ \ mu = \ frac {k} {\ beta} $.
Ogni parametro è un numero reale positivo. La distribuzione gamma è la distribuzione di probabilità di entropia massima guidata dai seguenti criteri.
Formula
$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ e \ è \ fixed. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ e \ è \ fisso. } $
Dove -
$ {X} $ = Variabile casuale.
$ {\ psi} $ = funzione digamma.
Caratterizzazione usando shape $ \ alpha $ e rate $ \ beta $
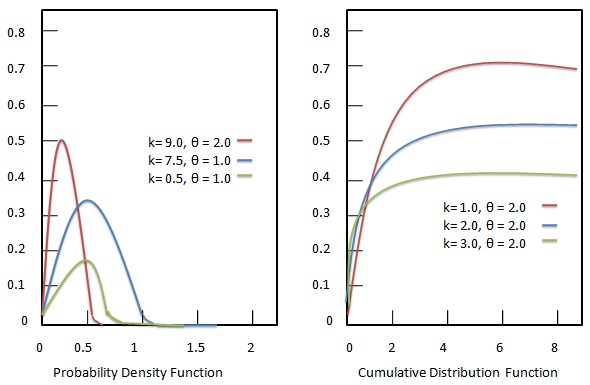
Densità di probabilità
La funzione di densità di probabilità della distribuzione Gamma è data come:
Formula
Dove -
$ {\ alpha} $ = parametro di posizione.
$ {\ beta} $ = parametro di scala.
$ {x} $ = variabile casuale.
Funzione di distribuzione cumulativa
La funzione di distribuzione cumulativa della distribuzione Gamma è data come:
Formula
$ {F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} } $
Dove -
$ {\ alpha} $ = parametro di posizione.
$ {\ beta} $ = parametro di scala.
$ {x} $ = variabile casuale.
$ {\ gamma (\ alpha, \ beta x)} $ = funzione gamma incompleta inferiore.
Caratterizzazione usando la forma $ k $ e la scala $ \ theta $
Densità di probabilità
La funzione di densità di probabilità della distribuzione Gamma è data come:
Formula
Dove -
$ {k} $ = parametro di forma.
$ {\ theta} $ = parametro di scala.
$ {x} $ = variabile casuale.
$ {\ Gamma (k)} $ = funzione gamma valutata in k.
Funzione di distribuzione cumulativa
La funzione di distribuzione cumulativa della distribuzione Gamma è data come:
Formula
$ {F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})} {\ Gamma (k )}} $
Dove -
$ {k} $ = parametro di forma.
$ {\ theta} $ = parametro di scala.
$ {x} $ = variabile casuale.
$ {\ gamma (k, \ frac {x} {\ theta})} $ = funzione gamma incompleta inferiore.