畳み込み定理

前回のチュートリアルでは、周波数領域の画像について説明しました。このチュートリアルでは、周波数領域と画像（空間領域）の関係を定義します。

この例を考えてみましょう。

周波数領域の同じ画像は、として表すことができます。

ここで、画像または空間ドメインと周波数ドメインの関係は何ですか。この関係は、畳み込み定理と呼ばれる定理によって説明できます。

空間領域と周波数領域の関係は、畳み込み定理によって確立できます。

畳み込み定理は次のように表すことができます。

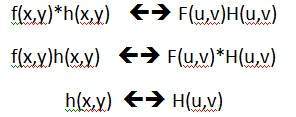
空間領域での畳み込みは周波数領域でのフィルタリングに等しく、その逆も同様であると言えます。

周波数領域でのフィルタリングは、次のように表すことができます。

The steps in filtering are given below.

周波数領域でのフィルターの概念は、畳み込みでのマスクの概念と同じです。

画像を周波数領域に変換した後、フィルタリングプロセスでいくつかのフィルタを適用して、画像に対してさまざまな種類の処理を実行します。処理には、画像のぼかし、画像の鮮明化などが含まれます。

これらの目的のための一般的なタイプのフィルターは次のとおりです。

次のチュートリアルでは、フィルターについて詳しく説明します。