周波数領域の紹介

多くの分野で画像を扱ってきました。現在、周波数領域で信号（画像）を処理しています。このフーリエ級数と周波数領域は純粋に数学であるため、その数学の部分を最小限に抑え、DIPでの使用にさらに焦点を当てます。

周波数領域分析

これまで、信号を分析したすべてのドメインで、時間に関して分析していました。しかし、周波数領域では、時間に関してではなく、周波数に関して信号を分析します。

空間領域では、画像をそのまま扱います。画像のピクセルの値は、シーンに対して変化します。一方、周波数領域では、空間領域でピクセル値が変化する速度を扱います。

簡単にするために、このようにしましょう。

単純な空間領域では、画像行列を直接処理します。一方、周波数領域では、このような画像を扱います。

まず、画像を度数分布に変換します。次に、ブラックボックスシステムは実行する必要のある処理を実行します。この場合のブラックボックスの出力は画像ではなく、変換です。逆変換を実行した後、画像に変換され、空間領域で表示されます。

それは絵で見ることができます

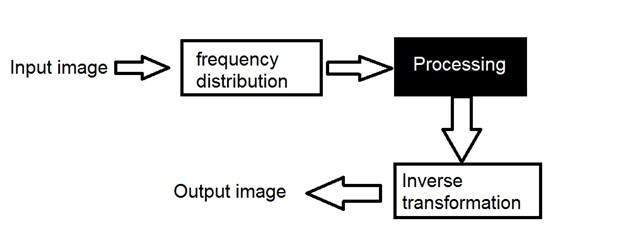
ここでは、変換という言葉を使用しました。それは実際にはどういう意味ですか？

信号は、変換と呼ばれる数学演算子を使用して、時間領域から周波数領域に変換できます。これを行う多くの種類の変換があります。それらのいくつかを以下に示します。

これらすべてのうち、次のチュートリアルでは、フーリエ級数とフーリエ変換について詳しく説明します。

空間領域の任意の画像は、周波数領域で表すことができます。しかし、この周波数は実際にはどういう意味ですか。

周波数成分を2つの主要な成分に分けます。

高周波成分は画像のエッジに対応します。

画像の低周波成分は滑らかな領域に対応します。