推論-コード化された2進数
2を底とする数は2進数として知られています。2進数は、0と1の補数で構成されます。したがって、コード化された2進数は2つのプロセスで構成されます。1つは2進数から10進数への変換で、もう1つは10進数から2進数への変換です。
10進数
何か知るために binary numberつまり、最初に10進数について知る必要があります。したがって、10進数は10桁で構成されます(つまり、0、1、2、3、4、5、6、7、8、9)。これらの数値を使用して、任意の10進法を表すことができます。たとえば、数字のシーケンスは2、4、6、および8です。次の方法で実行します。
2468 = 2×10 3 + 4×10 2 + 6×10 1 + 8×10 0
= 2468
Note−この場合、シーケンスのさまざまな桁に10の累乗を掛けて加算することにより、数値の値を取得します。ここで、この10は基数または基数と呼ばれます。したがって、10進法では、ベースは10です。
2進数
10桁を使用して decimal number; そのように、2進数を表すために2桁だけを使用します。これらの2桁、つまり0と1を使用して、任意の数値を表すことができます。
2進数の例は-1101です。ここでは、4桁が数字のシーケンス-1、1、0、1に存在します。次の方法で値を取得します。
1101 = 1×2 3 + 1×2 2 + 0×2 1 + 1×2 0
= 8 + 4 + 0 + 1 = 13
したがって、2進数は10進数で13を表します。値は次のように決定できますmultiplying different digits 2の累乗と加算によるシーケンスの。
Conventional method −上記の例では、任意の2進数の値を取得するために、次のルールを使用していることがわかります−
右から最初の桁は2で乗算される0 = 1
右から2桁目に21 = 2を掛けます
右から3番目の桁は2で乗算される2 = 4
同様に、右からn番目の桁に2n-1を掛けます
最後に、これらすべてが追加されます。
For Example −次の2進数を10進数に変換します。
A -1010
B -1111
C -100
D - 10000
Solution −
A - 1010 = 1×2 3 + 0×2 2 + 1×2 1 + 0×2 0
B - 1111 = 1×2 3 + 1×2 2 + 1×2 1 + 1×2 0
C - 100 = 1×2 2 + 0×2 1 + 0×2 0
D - 10000 = 1×2 4 + 0×2 3 + 0×2 2 + 0×2 1 + 0×2 0
より迅速な方法
Step I−与えられた数字の右桁から始めて、1、2、4、8、16、32……と書きます。左に進むと、各桁の下に続きます。
Step II−0未満の数値は無視してください。1未満のすべての数値を追加します。
この方法で例1を解いてみましょう。
A-1010
ここでは4桁が存在するため、1、2、4、8を使用します。
我々が得る、
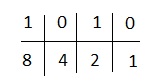
4と1はゼロを下回ります。それらを無視し、残りを追加します。8 + 2 = 10を取得します
このように、他の数を解くことができます。
10進数は、次の方法で2進数に変換できます。 successive divisions。除算のたびに、配当は2で除算されます。リマインダーが記録され、商が次の配当になり、再び2で除算されます。このプロセスは、除算が不可能になるまで繰り返されます。
例-17を2進数に変換します-
これ以上分割できなくなるまで、17を2で除算します。
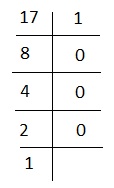
したがって、17のバイナリ形式は10001です。
Direction (Q. 1-4) − Study the following question and give the answer.
特定のコードでは、0の記号は+で、1の記号は#です。1より大きい数または記号はありません。1の記号の値は、1桁左にシフトするたびに2倍になります。
「0」は+として表されます
「1」は#として表されます
「2」は#+として表されます
「3」は##として表されます
「4」は#++などとして表されます
1 -次のうちどれが11を表しますか?
Options −
A -#+ ##
B -+ ## +
C -## ++
D -#+#++
E - どれでもない
Answer −オプションA
Explanation − 11に相当する値を得るには、2で連続除算する方法を使用します。

したがって、バイナリ形式は10111になります。1と0を#と+に置き換えると、#+ ##が得られます。
2 -次のうちどれが8を表しますか?
Options −
A -## ++
B -+ ## +
C -## ++
D -++ ##
E - どれでもない
Answer −オプションE
Explanation − 8の場合、次のようになります-
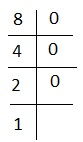
つまり、1000または#+++。正しい選択は5です。
3 -## +#で表されるのは次のうちどれですか?
Options −
A -8
B -11
C --13
D -12
E - どれでもない
Answer −オプションE
Explanation- ## +#= 1101 = 1×2 3 + 1×2 2 + 0×2 1 + 1×2 0 = 15
4 -次の番号のうち、#+++#で表されるのはどれですか?
Options −
A --22
B --31
C --14
D -17
E - どれでもない
Answer −オプションD
Explanation −#+ + +#= 10001
= 1×2 4 + 0×2 3 + 0×2 2 + 0×2 1 + 1×2 0
= 16 + 1 = 17
2進法は基数2、10進法は基数10、3進法は基数3、8進法は基数8です。3進法の場合、数値を表す3桁の数字があります。これらは0、1、および2です。この場合、数値は適切な3の累乗を掛けることによって10進数に変換されます。
For Example −
(12012)3 = 1×3 4 + 2×3 3 + 0×3 2 + 1×3 1 + 2×3 0 =(104)3