推論-論理的推論
論理的演繹は重要な章です。この章からの多くの簡単でマークを取得する質問がさまざまな競争試験に含まれているからです。この章では、このような問題を解決するための2つの方法について説明します。
- 三段論法
- ベン図法
基本
ステートメントが2つある場合は、三段論法が問題を解決するための最良の方法ですが、ステートメントの数が2つを超える場合は、ベン図法を使用してください。声明や結論は、一般的に受け入れられている事実から導き出されることもありますが、論理的でない場合もあります。例-
a)いくつかの椅子はドアです。
b)すべての男性は女性です
c)牛乳は白くない
結論に達するには、抽象的な思考が必要です。文の論理的意味を理解し、それに応じて結論に答える必要があります。各ステートメントは真実であると考える必要があり、結論がステートメントに論理的に従っているかどうかを検証する必要があります。
修飾子
これらは、あるものが他のものとどれだけ類似しているか、または異なっているかを説明するために使用される基本的な単語の一部です。いくつかの修飾子の例は、「All」、「Some」、「Some-not」などです。
ベン図の概念
一方、ベン図は、文や文を幾何学的図形で表現できるプロセスです。与えられたすべてのステートメントは、可能なベン図にプロットされます。次に、すべての結論がこれらの図で検証されます。すべてのベン図を満たす結論は、有効な結論と見なされます。
| ステートメント | 対応するベン図 |
|---|---|
| すべてAはBです |
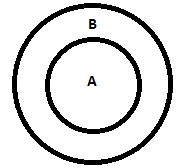
|
| 一部のAはB(または)一部のAはBではありません |
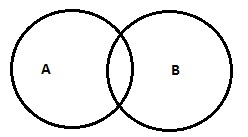
|
| いいえAはBです |
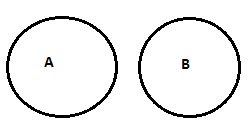
|
簡単な例を見て、もっとよく理解しましょう。
Sample − 1
Statements −
すべてのエンジニアはばかです。すべての愚か者は医者です。すべての医者は貧しい。
Conclusions −
I.一部の貧しい人々は愚か者です。
II。一部の貧しい人々はエンジニアです。
Options −
A −私だけが有効です
B −IIのみが有効です
C −両方のステートメントが有効です
D −いずれのステートメントも有効ではありません
Answer −オプションC
Explanation −
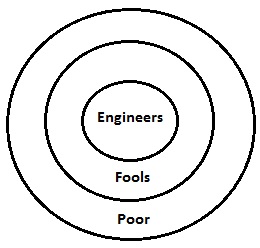
与えられたステートメントのベン図は上に描かれています。すべてのステートメントが1か所に図式的に表示されます。ここで、結論について1つずつ話し合うと、すべてが明確になります。
ここで愚か者は貧しい人々のサブセットです。ですから、一部の貧しい人々が愚か者になることは明らかな事実です。したがって、結論Iは有効です。同様に、エンジニアも貧困層のサブセットであるため、結論IIは有効です。したがって、両方のステートメントが有効になります。
Sample − 2
Statements −
一部のキーボードはマウスです。一部のマウスはラジオです。
Conclusions −
I.一部のキーボードはラジオです。
II。一部のラジオはキーボードです
III。すべてのラジオはマウスです。
IV。すべてのマウスはキーボードです。
Options −
A −結論Iのみが有効です
B −結論IIのみが有効です
C −IまたはIIのいずれかが有効です
D −結論はどれも有効ではありません
E −IとIIの両方が有効です
Answer −オプションD
Explanation −両方のステートメントが特定であるため、明確な結論は有効ではありません。
Sample − 3
Statements −
すべての学生は冷静です。すべての学生はいたずらです。
Conclusions −
I.すべてのいたずらは地味であるかその逆です。
II。一部の地味な人はいたずらです。
III。一般的にいたずらは地味です。
IV。犯罪と罪悪感は一緒に行きます。
Options −
A −結論Iのみが有効です
B −結論IIのみが有効です
C −IまたはIIのいずれかが有効です
D −IまたはIIのいずれも有効ではありません
E −IとIIの両方が有効です
Answer −オプションB
Explanation−中間用語「学生」はステートメントで2回配布されているため、結論を広めることはできません。だから、「何人かの地味な人はいたずらだ」というのは正当なことです。したがって、IIが当てはまります。