推論-キューブと直方体
今日では、「キューブと直方体」に基づく質問がほぼすべての競争試験で出されています。これらの問題は、さまざまな競争試験で非常に頻繁に発生します。
以下に説明する方法は、シンプルでありながらエレガントです。それらは非常に理解しやすく、少し練習すれば習得する必要があります。立方体は、6つの面、12のエッジ、およびコーナーを持つ3次元の立体です。立方体のすべてのエッジは等しく、すべての面は正方形です。これは、6つの面を持つ立体図です。正方形である各面はと呼ばれますa cube。6つの面のそれぞれが長方形である場合、それは呼び出されますcuboid。直方体は、rectangular parallelepiped。
立方体と直方体について尋ねられる質問は、次のタイプである可能性があります。
タイプI
完全な立方体のいくつかのビューが表示され、立方体のどの部分が特定の部分の真下にあるかを見つける必要があります。
タイプII
開いた立方体が与えられ、立方体に閉じたときにどのように見えるかを予測する必要があります。
タイプIII
立方体は、同じ色または異なる色でその面の一部にニスを塗ってから、特定の数の同じ部分にカットすることができませんでした。次に、フォームの質問-「2つの面にニスを塗った小さな立方体はいくつありますか?」「片面だけにニスを塗った小さな立方体はいくつありますか?」等
試験に現れる問題には2つのタイプがあります。最初に、あなたはいくつかのビューを与えられますcomplete cube、およびキューブのどの部分が特定の部分の真下にあるかを指定する必要があります。別のタイプでは、あなたは与えられますopened-up cube、そしてそれが立方体に閉じられたときにどのように見えるかを予測する必要があります。
For Example −
立方体のいくつかの面を以下に示します-

2の反対にあるのはどの数字ですか?
A − 1
B − 6
C − 5
D − 4
基本的なアプローチは次のとおりです-
タイプI
A fundamental rule: Opposite cannot be together;
3つの面しか見えない立方体を見ると、2つの反対側の面を一緒に見ることはできません。これらすべてのルールを使用すると、上記のタイプの問題を簡単に解決できます。特定の面の反対側の面を見つける必要がある上記の質問では、任意のビューでXと一緒に発生した面を削除できます。したがって、他のすべての選択肢を排除することができ、残りが私たちの答えになります。
この時点で、前の段落をもう一度読んで、概念を理解していることを確認する必要があります。この後、上記の例を解決して、上記の概念を適用できるかどうかを確認する必要があります。ただし、概念を完全に理解していないことがわかります。問題ありません。このセクションを読み続けてください。セクションを終了すると、状況が明らかになります。前述の基本的なルールを念頭に置いて、上記のタイプの質問を解決できます。
質問については、ルール自体で十分です。その後、あなたはそれをより迅速に解決することができますthree secondary rules。
Solution for above example −
与えられた例では、2の反対側の顔を見つける必要があります。最初の図では、2が1と3とともに表示されています。これは、1と3のどちらも2の反対になることはできないことを意味します。同様に、3の反対側には、4、5、または6のいずれかがあります。次に、2番目の図を見てください。ここで、3と1は5と一緒に発生します。これは、5が3と1のどちらとも反対ではないことを意味します。つまり、4または6のいずれかが1の反対で、もう一方が3の反対であるため、5は2の反対である必要があります。したがって、5は正しいです。回答。
いくつかのより速いルール
今、あなたはそのような質問を解決する基本的なトリックを理解しているに違いありません。秘訣は、不可能な選択を排除することです。このために、2つの面が互いに反対である場合、立方体の1つのビューで同時に発生することはできないという基本的なルールを利用します。しかし、今日の時間のかかる大会では、コンセプトだけではうまくいきません。あなたは質問を素早く解決できなければなりません。質問を解決するためのいくつかの二次的なルールがあります。
Rule I−その図をXと呼びましょう。その反対を見つけなければなりません。立方体のいずれかのビューで、XがYとZとともに表示されるとします。3番目の図(たとえばA)とともに、XはAの反対側になります。
たとえば、2の反対側の顔を見つける必要があります(これは私たちのXです)。これで、2が1と3(YとZ)とともに1つの図に表示されます。また、1と3は、5とともにもう1つの図に一緒に表示されます(つまりA)。したがって、2は5の反対でなければなりません。
Rule II−「X」の反対側の面を見つける必要があります。立方体のいずれかのビューで、XがYとZとともに表示されるとします。ここで、YとZがそれ以上のビューに一緒に表示されないが、2つ以上の異なるビューに別々に表示されるとします。次に、YとZが別々に表示される2つのビューに共通する図は、Xの反対側の図になります。
Rule III−図Xと呼びましょう。その反対を見つけなければなりません。ここで、Xが2つのビューに表示され、これら2つのビューに4つの異なる図がXとともに表示されるとします。次に、これら2つのビューにXが表示されない唯一の図は、Xの反対側にある必要があります。
Summary−基本的なルールを心の奥底に置き、3つの二次的なルールを適用して迅速に回答する必要があります。全体のアプローチは、次の図で要約できます。
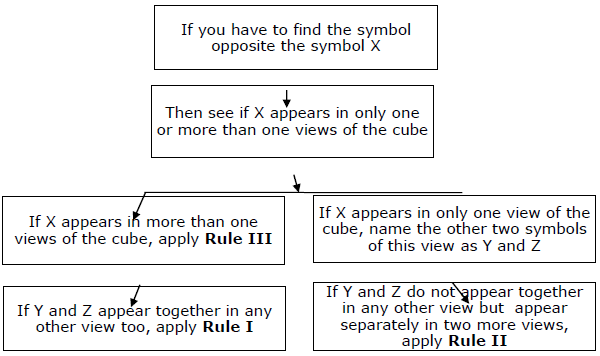
タイプII
このタイプでは、基本的なルールを使用します。このルールは、反対側の面が1つのビューに表示される組み合わせを排除するのに役立ちます。したがって、「」を見て、どちらの面が互いに反対になるかを判断する方法を知っていれば、選択の排除につながります。opened-up cube」。この目的のために、あなたが見ることによってあなたが知ることができる非常に単純なルールがありますopened-up cube、見ているだけで向かい合う面になります。
ルールは以下のとおりです。
Third is opposite rule −
顔の反対側の顔(たとえばX)を見つけたい場合は、図I、II、IIIを参照してください。開いた立方体が与えられます。立方体が閉じているときに、どの面が互いに反対側にあるかを見つける必要があります。
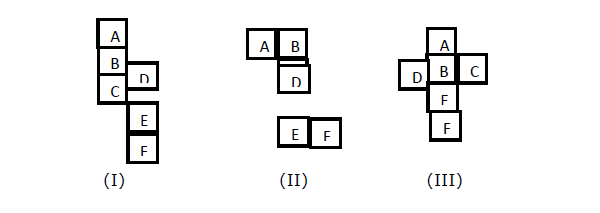
Explanation −
図(I)では、Aの3番目の図はCです。したがって、AはCの反対です。したがって、DとFは反対になります。BとEは反対になります。
図(II)では、BはDの3番目であるため、BはDの反対になります。同様に、CはEの反対になり、AはFの反対になります。
図(III)では、AはEの反対、BはFの反対です。したがって、CはDの反対です。
Steps to solve problem
これで、このタイプの質問を解決できます。私たちは、を見て反対の顔を見つける方法を知っていますOpened-up cube。また、立方体のどのビューでも、反対側の面を一緒にすることはできないこともわかっています。したがって、2つのルールを組み合わせると、問題を簡単に解決できます。
概要
これで、タイプIIの質問を解決する方法についての説明が完了しました。3番目のルールを使用して、どの面が互いに反対であるかを判別する必要があります。次の図は、このアプローチに関する完全な情報を示しています。

タイプIII
Counting of Cubes (when a varnished solid cube is cut);
前のセクションでは、立方体の反対側の面を見つける問題について説明しました。立方体に関連する別のタイプの質問があります。異なる色が異なる面にニスを塗った大きな立方体がいくつかの小さな立方体に分割され、片面のみまたは両面にニスを塗った立方体の数を見つける必要があります。
Format of this problem −
Example −
立方体の側面には緑、青、赤の3色が塗られており、すべての色が立方体の2つの反対側の面に塗られています。これで、キューブは同じサイズの64個のキューブに分割されます。この情報に基づいて、次の質問に答えてください-
1.両面にニスを塗り、残りの面にニスを塗っていない立方体はいくつありますか?
A − 18
B − 20
C − 22
D − 24
2.片面だけにニスを塗った立方体の数(緑色または青色のみ)
A − 4
B − 24
C − 16
D − 12
3.側面にニスが塗られていない立方体はいくつありますか?
A − 0
B − 8
C − 12
D − 64